【统计模型】基于SARIMA和ARIMA统计预测模型研究（Python代码实现）

👨‍🎓个人主页：研学社的博客    

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

1.1 ARIMA模型

1.2 SARIMA

📚2 运行结果

2.1 ARIMA模型

2.2 SARIMA

🎉3 参考文献

🌈4 Python代码实现

---

​

💥1 概述

1.1 ARIMA模型

ARIMA模型，也称为求和自回归移动平均自模型，实际上根检验。ADF检验是判断时间序列是否存在单位根：如果不存是差分运算与ARMA模型的结合。ARIMA（p,d,q）模型记为：

​

 

获得观察值时间序列后，通过以下步骤完成ARIMA建模分析过程：

（1）对时间序列数据进行平稳性检验。如果该序列不平稳，转步骤（2）；若该序列平稳，再进行白噪声检验，若为序表1 原序列及一阶差分序列ADF检验列检验为白噪声，模型终止；若不是白噪声，转步骤（3）。

​

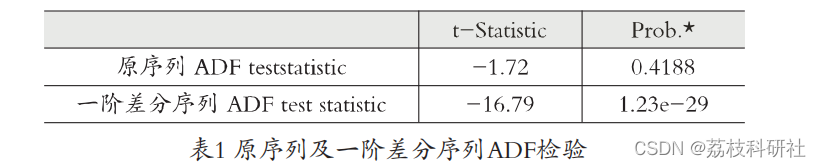
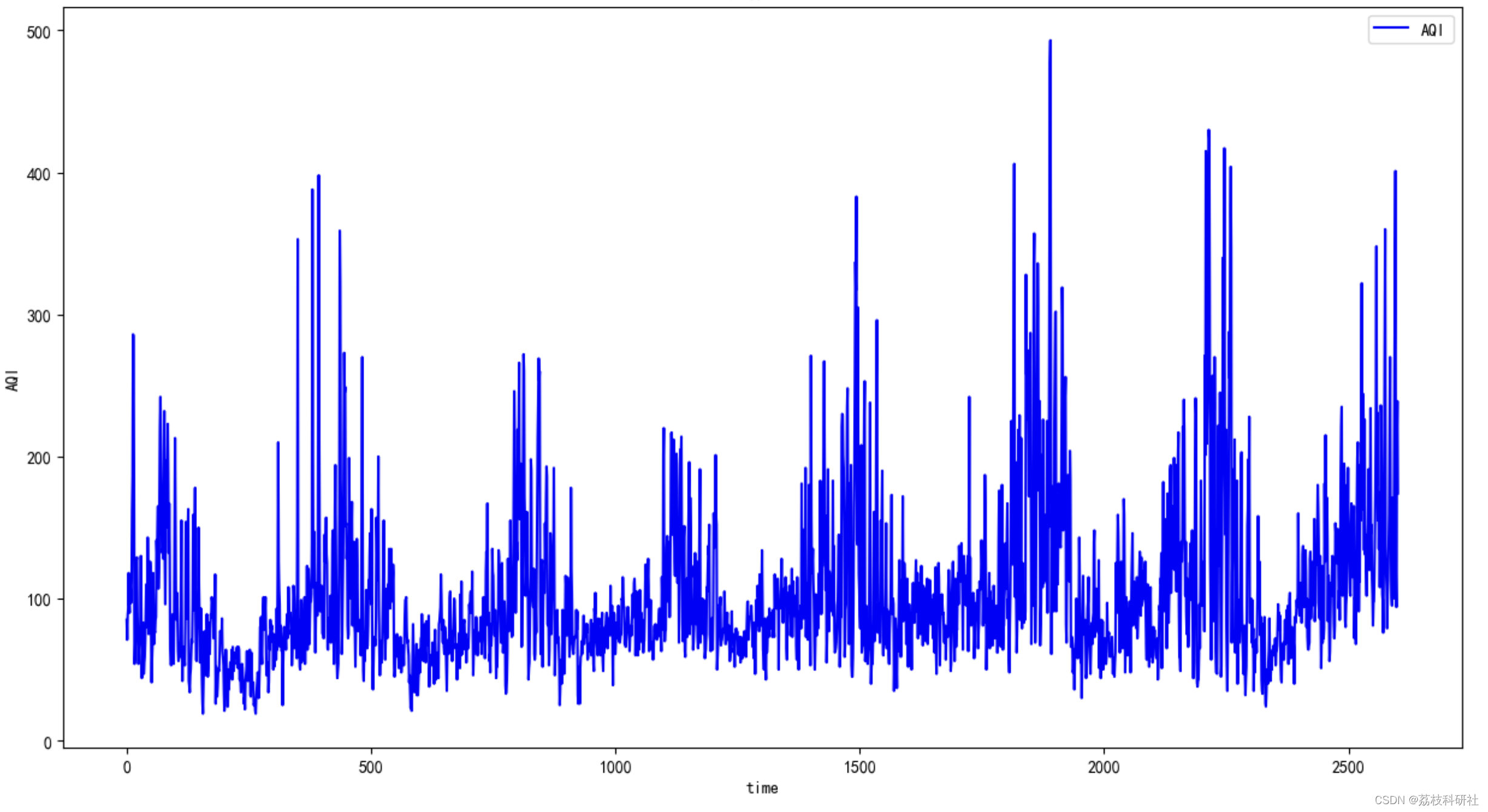
 可以看出，一阶差分后序列的p值为1.23e-29，远小于0.05,因此认为一阶差分后的序列平稳。也可以通过绘制折线图，观察时间序列的平稳性，如图1所示，原序列的时序图呈现下降趋势，从最高点320下降到190左右，显然原序列不平稳;一阶差分后的时序图围绕一个常数值上下波动，且波动范围不大，认为一阶差分后的序列是平稳的。

（2）当时间序列处于不平稳时，可通过d阶差分使非平稳

（3）求解观测序列的样本自相关系数（ACF）和偏自相关势，从最高点320下降到190左右，显然原序列不平稳；一阶差系数（PACF）的值。分后的时序图围绕一个常数值上下波动，且波动范围不大，认

（4）根据样本自相关系数和偏自相关系数表现出来的截尾为一阶差分后的序列是平稳的。性和拖尾性质，确定p和q的值，对ARIMA（p,d,q）模型进行拟合。

（5）估计模型中的未知参数的值。

（6）通过残差序列白噪声检验，说明模型的有效性。如果拟合模型不通过检验，转向步骤（4），调整p和q的值，重新拟合模型。

（7）利用拟合模型ARIMA（p,d,q），预测该时间序列未来几期的数值。

1.2 SARIMA

季度性差分自回归滑动均衡模型（ SARIMA 模型）是差分自回归移动平均模型（ARIMA 模型）的改良模型，将非平滑时间序列转换为平滑周期序列，同时将因变换为仅通过对其落后值和随机误差项的现值和落后值加以返回 [10] 。因为该模式不仅可以对非规则的非平滑的时间序列数据加以分

析，并且把时间序列数据中常见的季节特性也作为考虑，所以适用于中等甚至更多长度的时间序列数据模型 [11] 。记为原始周期序列的 yt ，其 SARIMA 模型的实质上是先对 yt 进行逐期差分，先去掉周期序列的趋势性，而后实行季度差分，再去掉季度性。后经以上所述处理过程，所形成的模型就可以表示为：

 

📚2 运行结果

2.1 ARIMA模型

# 显示原数据
plt.figure(figsize=(15, 8))
plt.title('AQI')
plt.xlabel('time')
plt.ylabel('AQI')
plt.plot(df, 'blue', label='AQI')
plt.legend()
plt.show()

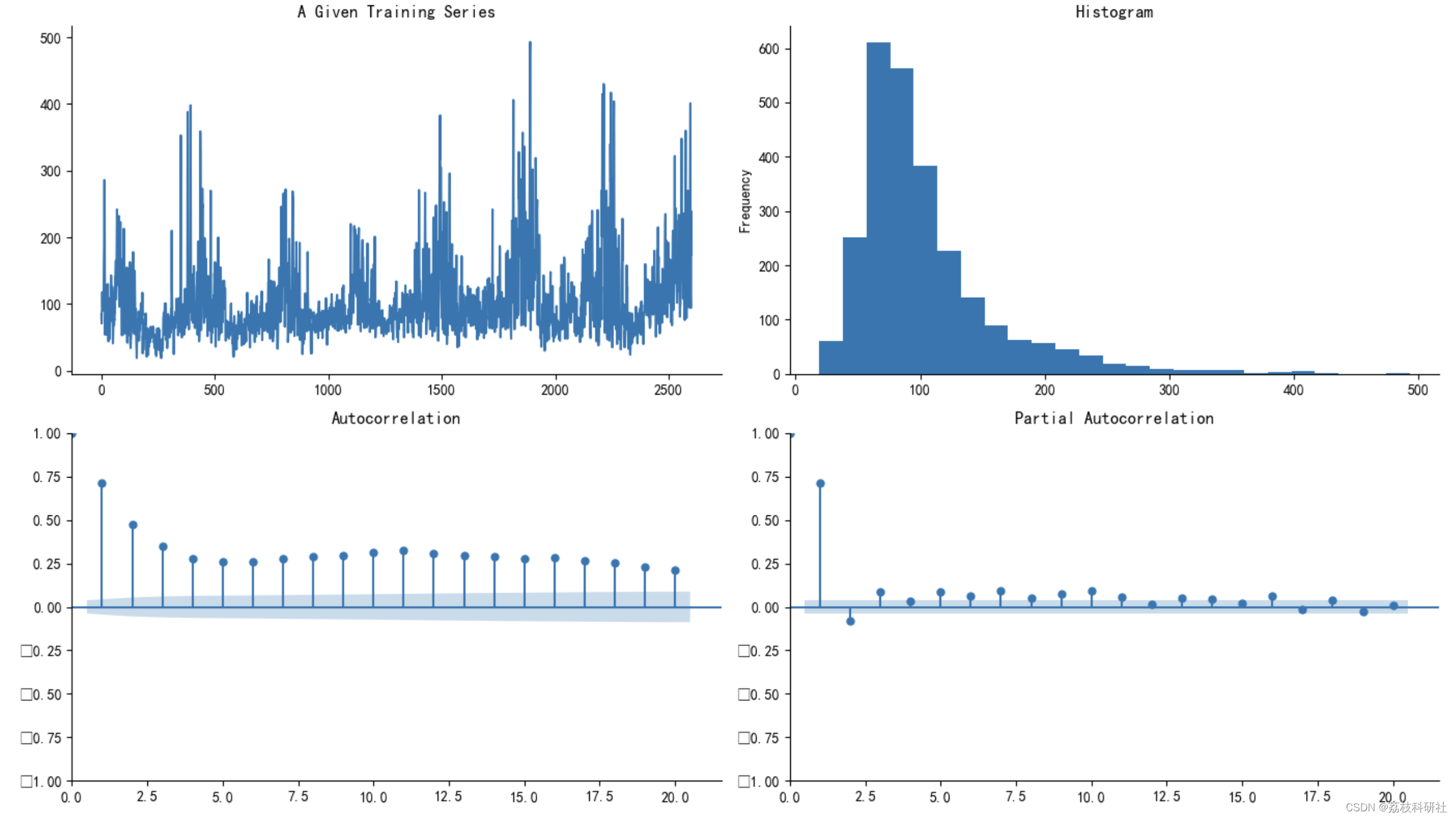
##自相关和偏自相关
tsplot(ts_data, lags=20)

train_data, test_data = df[0:int(len(df)*0.8)], df[int(len(df)*0.8):]
#画出训练集和测试集的原数据（open 价格）
plt.figure(dpi=100, figsize=(40,12))
plt.title('Air Quality Index of Nanning City', size=40)
plt.xlabel('time/day',size=30)
plt.ylabel('AQI',size=30)
plt.plot(train_data, 'b', label='Training Data',linewidth=3)
plt.plot(test_data, 'g', label='Testing Data',linewidth=3)
font = {'serif': 'Times New Roman','size': 30}
plt.rc('font', **font)
plt.legend()
plt.show()

#显示预测结果和原数据
plt.figure(figsize=(10,5))
plt.plot(df, 'green', color='blue', label='Training Data')
plt.plot(test_data.index, predictions, color='green', marker='o', linestyle='dashed', label='Predicted Price')
plt.plot(test_data.index, test_data, color='red', label='Actual Price')
plt.title('AQI')
plt.xlabel('time')
plt.ylabel('AQI')
plt.legend()
plt.show()

 

 

#只显示预测部分，不显示训练数据部分
plt.figure(figsize=(12,7))
plt.plot(test_data.index, predictions, color='green', marker='o', linestyle='dashed',label='Predicted Price')
plt.plot(test_data.index, test_data, color='red', label='Actual Price')
plt.title('营业收入')
plt.xlabel('time')
plt.ylabel('AQI')
plt.legend()
plt.show()

2.2 SARIMA

# 显示原数据
plt.figure(figsize=(15, 8))
plt.title('风速')
plt.xlabel('时间')
plt.ylabel('最大风速')
plt.plot(df, 'b', label='AQI')
plt.legend()
plt.show()

##自相关和偏自相关
tsplot(ts_data, lags=20)

train_data, test_data = df[0:int(len(df)*0.8)], df[int(len(df)*0.8):]
#画出训练集和测试集的原数据（open 价格）
plt.figure(dpi=100, figsize=(40,12))
plt.title('Air Quality Index of Nanning City', size=40)
plt.xlabel('time/day',size=30)
plt.ylabel('AQI',size=30)
plt.plot(train_data, 'b', label='Training Data',linewidth=3)
plt.plot(test_data, 'g', label='Testing Data',linewidth=3)
font = {'serif': 'Times New Roman','size': 30}
plt.rc('font', **font)
plt.legend()
plt.show()

#只显示预测部分，不显示训练数据部分
plt.figure(figsize=(12,7))
plt.plot(test_data.index, predictions, color='b', marker='o', linestyle='dashed',label='Predicted')
plt.plot(test_data.index, test_data, color='red', label='Actual')
plt.title('SARIMA')
plt.xlabel('time')
plt.ylabel('AQI')
plt.legend()
plt.show()

 

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]王沛智,梅栴,高巍.基于SARIMA模型的黄金价格预测[J].电子技术与软件工程,2022(23):233-237.

[2]黄梦婷.基于ARIMA模型的股票价格预测实证研究[J].内江科技,2023,44(03):61-62.

🌈4 Python代码实现