使用航空航天模块的国际航线规划模拟器研究（Matlab代码、Simulink仿真实现）

荔枝科研社

于 2025-04-22 09:31:27 发布

阅读量644

点赞数 29

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147408787

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

使用航空航天模块的国际航线规划模拟器研究

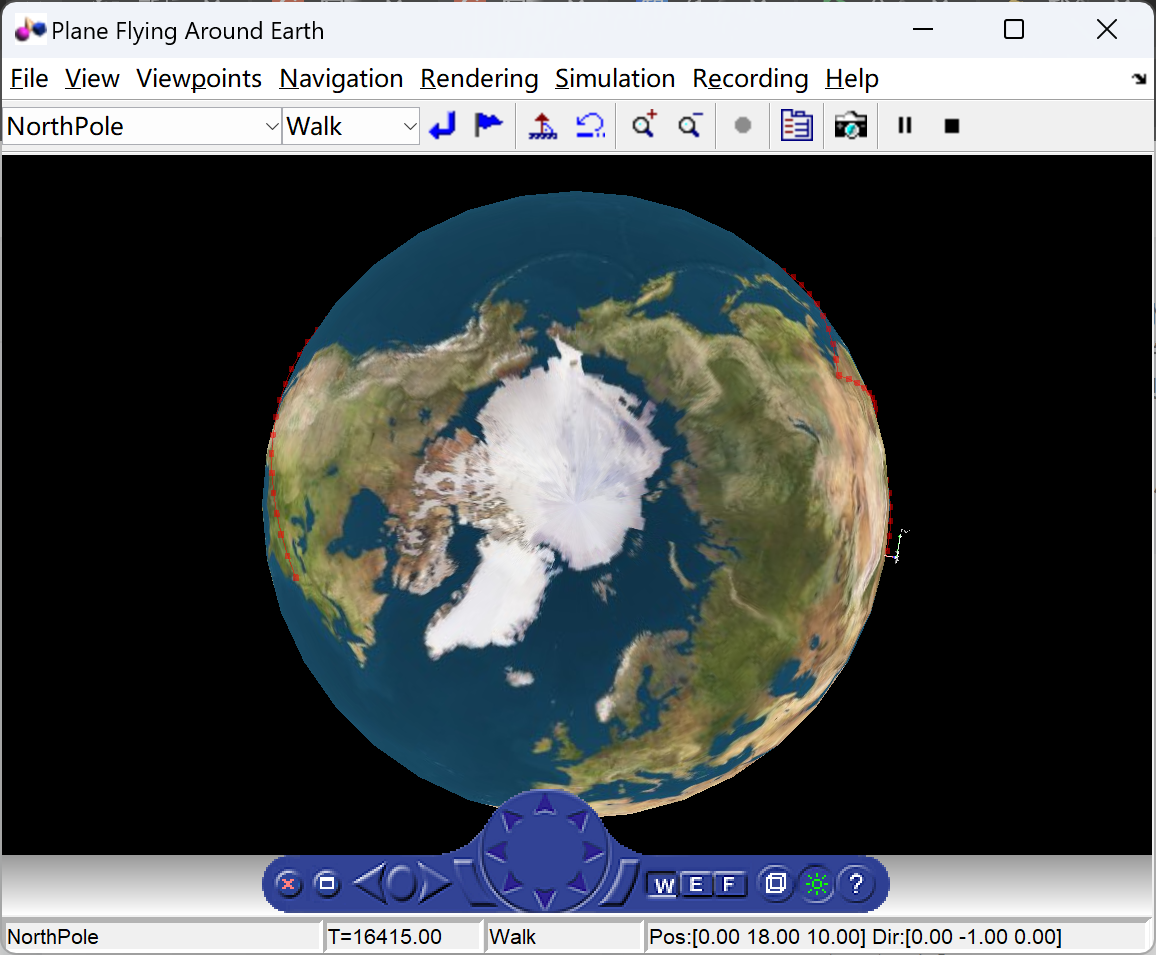
在这个演示中，以一个包含纬度和经度的城市的有序列表作为输入，模拟器计算两个连续城市之间的最短路径，然后在追踪轨迹的同时在3D地球上动画显示飞机的运动。请注意，这是一个在MATLAB中完成数据分析并在Simulink中“回放”数据的示例。
此外，飞机上还附有一个东北向（NED）框架，可以更好地理解飞机坐标系。

一、引言

随着全球航空业的快速发展，国际航线规划成为航空公司运营中的关键环节。为了优化航线、提高飞行效率并降低运营成本，开发一个能够精确计算最短路径并在3D环境中动画显示飞机运动的国际航线规划模拟器显得尤为重要。本文介绍了一个基于MATLAB和Simulink的模拟器，该模拟器利用航空航天模块实现了上述功能。

二、系统架构

输入数据：
- 包含纬度和经度的城市有序列表。
核心模块：
- MATLAB：用于数据处理、路径计算和轨迹生成。
- Simulink：用于3D动画显示和飞机运动模拟。
航空航天模块：
- 提供飞行力学、导航和制导算法，支持飞机在3D空间中的运动模拟。

三、功能实现

路径计算：
- 利用MATLAB中的地理信息系统（GIS）工具箱，根据输入的城市列表计算两个连续城市之间的最短路径。
- 考虑地球曲率和大气条件对飞行路径的影响，进行必要的修正。
轨迹生成：
- 根据计算出的最短路径，生成飞机的飞行轨迹。
- 轨迹包括飞行高度、速度、航向等参数，确保飞行过程的安全和效率。
3D动画显示：
- 在Simulink中搭建3D地球模型，将计算出的飞行轨迹映射到地球表面。
- 实时动画显示飞机的运动过程，包括起飞、飞行和降落阶段。
- 提供视角切换、缩放和旋转功能，方便用户从不同角度观察飞行轨迹。
飞机坐标系：
- 在飞机上附加一个东北向（NED）框架，用于表示飞机的姿态和位置。
- NED框架包括北（N）、东（E）和地（D）三个方向，有助于用户更好地理解飞机在3D空间中的运动状态。

四、技术细节

MATLAB数据处理：
- 使用MATLAB的脚本语言编写数据处理算法，包括路径计算和轨迹生成。
- 利用MATLAB的图形绘制功能，生成飞行轨迹的二维和三维图形。
Simulink动画设计：
- 在Simulink中搭建3D地球模型，使用航空航天模块中的飞行力学和导航算法。
- 设计动画控制器，根据飞行轨迹数据控制飞机的运动。
- 添加交互界面，允许用户输入城市列表、选择飞行参数和查看动画结果。
模块集成：
- 将MATLAB中的数据处理算法与Simulink中的3D动画模型进行集成。
- 实现数据在MATLAB和Simulink之间的实时传输和同步。

五、应用前景

航空公司运营优化：
- 通过精确计算最短路径和动画显示飞行轨迹，帮助航空公司优化航线规划。
- 提高飞行效率，降低运营成本，增强市场竞争力。
飞行训练：
- 利用模拟器进行飞行训练，提高飞行员的飞行技能和应对突发情况的能力。
- 通过模拟不同飞行条件和场景，增强飞行员的实战经验和安全意识。
科研与教育：
- 为航空航天领域的科研工作者提供实验平台，支持飞行力学、导航和制导算法的研究。
- 作为航空航天专业的教学工具，帮助学生理解飞行原理和运动规律。

六、结论

本文介绍了一个基于MATLAB和Simulink的国际航线规划模拟器，该模拟器利用航空航天模块实现了最短路径计算、轨迹生成和3D动画显示等功能。通过该模拟器，用户可以直观地观察飞机的运动过程，优化航线规划，提高飞行效率。未来，我们将继续完善模拟器的功能，提高计算精度和动画效果，为航空公司的运营优化和飞行训练提供更加有力的支持。

📚2 运行结果

部分代码：

% City 6: Teheran Iran 35 45 N 51 45 E
latitude(6,1)=35+45/60;
longitude(6,1)=51+45/60;

% City 7: Rome, Italy 41 54 N 12 27 E
latitude(7,1)=41+54/60;
longitude(7,1)=12+27/60;

% City 8: London 51 32 N 0 5 W
latitude(8,1)=51+32/60;
longitude(8,1)=-5;

% City 9: Mexico 19 26 N 99 7 W
latitude(9,1)=19+26/60;
longitude(9,1)=-99-7/60;

% Scaling calculations

% If the aircraft moves along the great circle fully, then use 20,000
% points to sample that interval. If not, scale it.
t_scaled=2*10000/360;

% These two variables will help in creating the complete list of latitudes
% and longitudes for all the N cities
t_index=1;
t_span=1;

% Assess the size of the final array that you need to initialize that will
% store all the latitudes and longitudes for the animation. This will
% eventually be fed as a vector into the Simulink model. The Simulink model
% has the appropriate transformations to transform this data for animation.
for i=1:N
k=mod(i,N)+1;
t_span=round(t_scaled*distance(latitude(i,1),longitude(i,1),latitude(k,1),longitude(k,1)));
t_index=t_index+t_span-1;
end
LL=zeros(t_index, 2);
% Reinitializing t_index because we want to use it again
t_index=1;