基于混沌系统和DNA编码的彩色数字图像加密、解密、抗噪声性能分析以及抗裁剪性能分析（Matlab代码实现）

荔枝科研社

于 2025-05-04 10:45:44 发布

阅读量691

点赞数 23

文章标签： matlab 网络算法

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147692411

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

2.1 基于混沌系统与DNA编码的彩色数字图像加密系统

2.2 基于混沌系统与DNA编码的彩色数字图像解密系统

2.3 包含内容yyds

🎉3 参考文献

🌈4 Matlab代码、文章下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

近年来，图像数据信息的安全性逐渐受到人们的关注，为了保证图像的可靠传输，混沌系统被引

入图像加密技术。本文主要研究了两种基于混沌系统的图像加密方案。第一种方案是基于超混沌系统和 DNA 编解码运算相结合的图像加密算法，该算法对图像分块进行加密，由混沌系统生成的混沌序列决定每一图像块的 DNA 编解码和运算方式。针对该算法密钥空间较低以及不能抵御裁剪攻击的问题，本文增加了算法中混沌系统的个数，优化了加密的流程。仿真结果表明改进后的加密算法密钥容量提升至 10127 数量级，可以抵抗穷举密钥攻击；加密后图像相邻元素相关性降低至 10-3 数量级，且加密后图像具备抗裁剪性能。另一方面，基于超混沌系统和 DNA 编解码运算的加密算法复杂度较高，不适用高效图像加密应用场景，因此本文又研究了基于混沌系统和离散余弦变换（DCT）相结合的图像加密压缩算法。此类算法可以在保证图像安全性的同时对图像数据进行压缩，从而提升图像传输的效率。鉴于传统混沌系统 DCT 加密算法的加密过程比较单一，本文在此基础上引入了符号加密，并且将加密后的结果存储为一维数据。仿真结果表明改进后算法的密钥容量达到 1074 数量级。当压缩率低于 64:10 时，解密后还原的图像在视觉效果上和原始图像区别较小，同时，可以根据实际需要，更改压缩矩阵从而获得不同的压缩率，从而提升图像的传输效率。

关键词：图像加密；混沌系统；DNA 编解码运算；离散余弦变换

本文主要研究基于混沌系统的数字图像加密算法，在研究了相关文献后，对两种以混沌系统为核心的图像加密算法进行了改进和优化，并分别对优化后的两种图像加密算法进行仿真与性能测试。一种是基于 Chen 超混沌系统、Logistic 混沌系统和 DNA 编码运算解码相结合的彩色数字图像分块加密算法。此算法的原理是将待加密图像和 Logistic 混沌矩阵分块进行 DNA编码，之后对二者相同位置的图像块之间进行 DNA 运算和解码，最后得到加密后的图像。其中，Chen 超混沌系统生成的混沌序列决定了图像块的 DNA 编码、运算和解码方式。本文对上述算法主要做了以下几点优化：

（1）增大密钥容量。加密算法使用了一个 Chen 超混沌系统和三个 Logistic 混沌系统，增加了加密时的密钥个数，密钥容量提升至10127数量级，足以抵抗穷举密钥攻击，增强了算法的安全性。

（2）通过增加 DNA 运算法则的种类，进一步降低密文图像相邻元素的相关性至10−3数量级，提升了密文图像的混乱程度，增强了算法的安全性。

（3）增加置乱操作。为使加密算法符合 Shannon 提出的置乱-扩散准则，由 Logistic系统生成两个混沌序列，对加密后图像的 R、G、B 三个通道分别进行行置乱和列置乱操作，此举同时提升了密文图像的抗裁剪性能。经仿真验证，改进后的加密算法密钥容量极大、对密钥的敏感性极高、相邻位置数据值关联性极弱、密文图像直方图分布均匀、信息熵接近极限值、密文图像抗噪声能力与抗裁剪能力较强，十分适用于数字图像的加密。本文研究的另一种算法是基于 Logistic 混沌系统和 DCT 变换相结合的灰度图像频域加密压缩算法。此算法的原理是将待加密图像进行 DCT 变换至频域，去除低频数据，对剩余数据进行置乱加密后得到加密结果。本文对上述算法进行了如下优化：

（1）增大密钥容量。加密算法使用了两次 Logistic 混沌系统，密钥容量达到了1074数量级，增强了算法的安全性。

（2）将二维图像数据压缩为一维数据，降低了算法的时间和空间复杂度。

（3）频域加密时引入了符号加密，即对序列元素进行符号的随机变换，与置乱加密共同形成了置乱-扩散的效果。经仿真验证，此加密算法密钥敏感性强，密钥空间大，可以抵抗穷举密钥攻击。同时，可以根据实际需要，更改压缩矩阵从而获得不同的压缩率。根据仿真结果显示，当压缩率低于 64:10 时，经过解密解压后还原的图像在视觉效果上和原始图像区别较小，说明此算法的压缩性能较强，在对解密后图像质量要求不高的情况下，至少可以提供高于 6 倍的压缩率，从而提升图像的传输效率。全部资源下载见第4部分。

📚2 运行结果

2.1 基于混沌系统与DNA编码的彩色数字图像加密系统

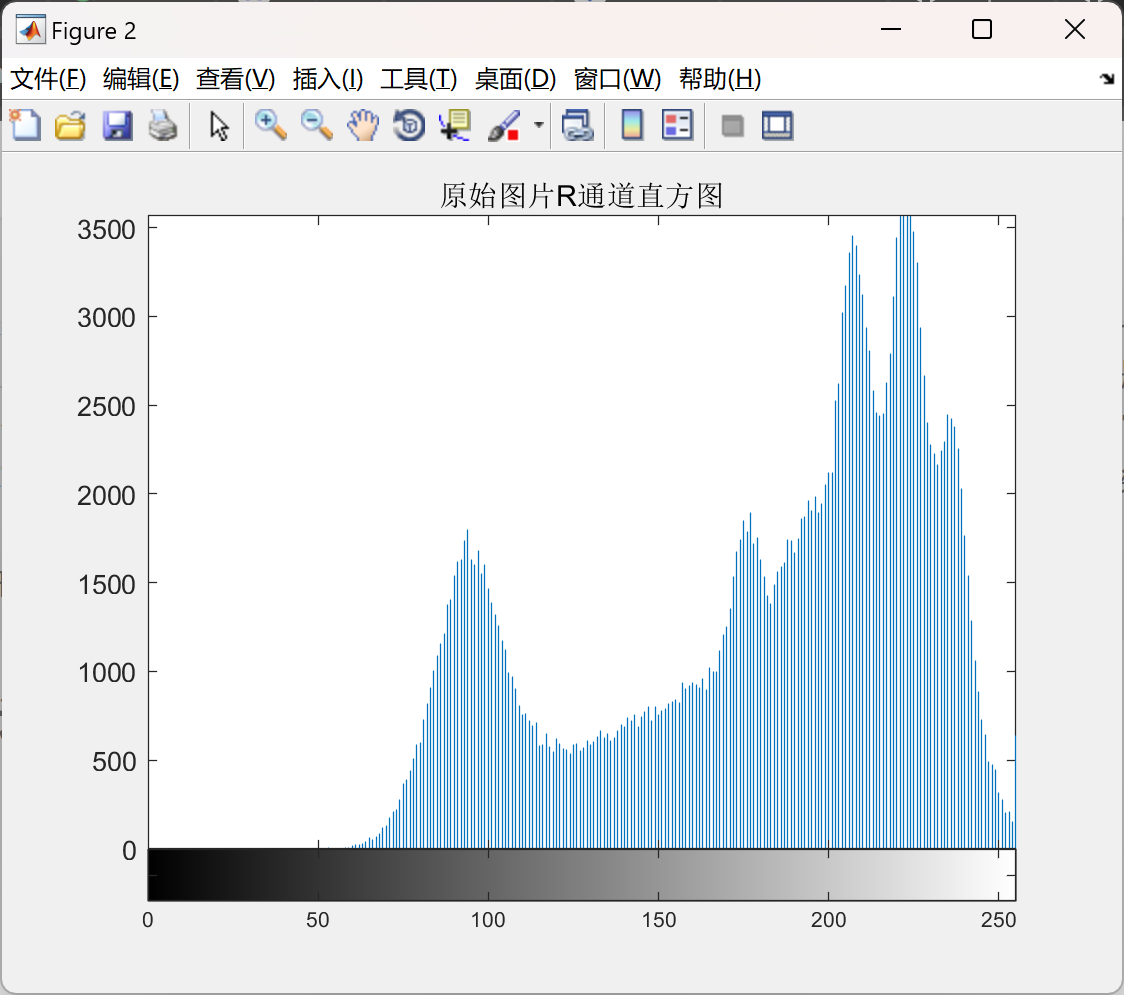
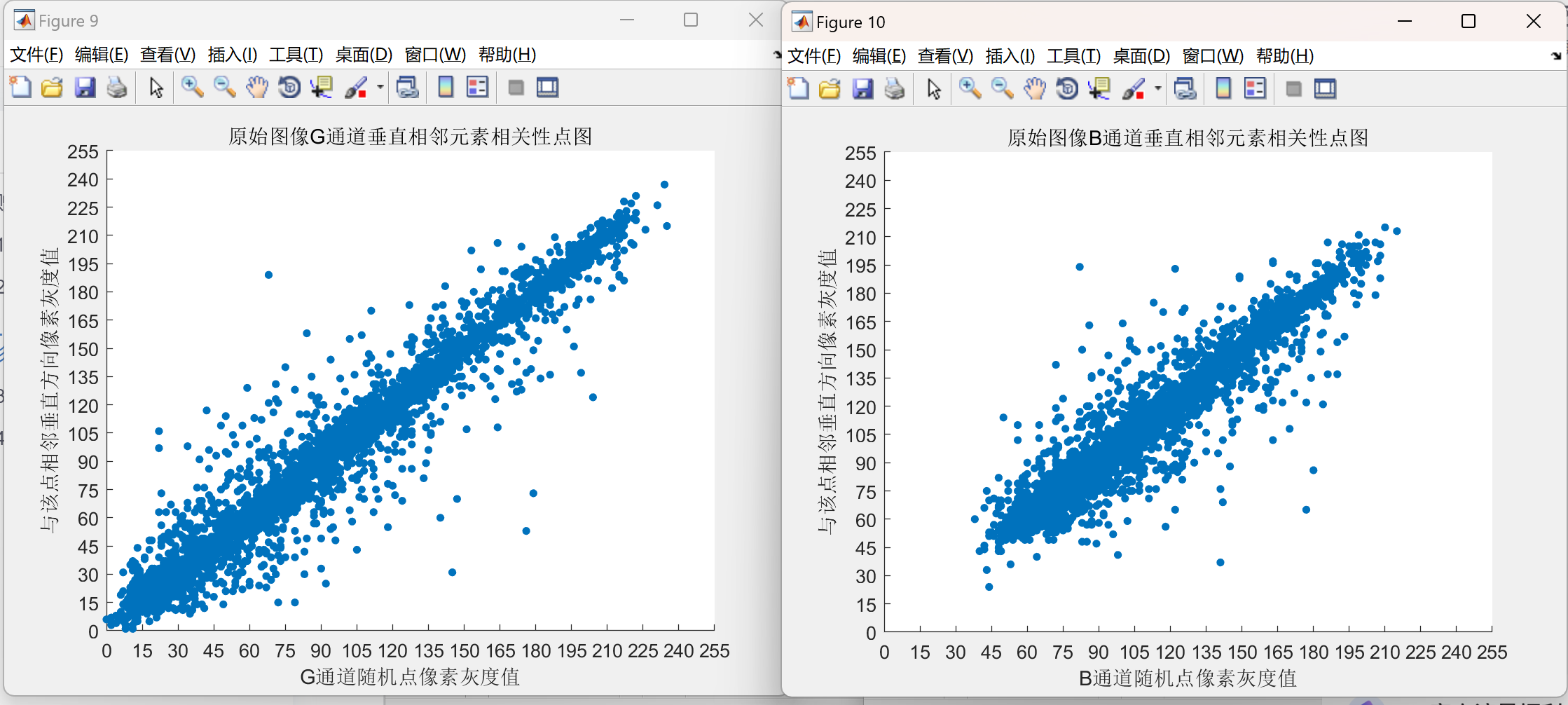
运行结果较多，就不一一展示。

2.2 基于混沌系统与DNA编码的彩色数字图像解密系统

2.3 包含内容yyds

本文含全部文章代码，很值得学习。超级棒

部分代码：

%% 2.产生Logistic混沌序列
% u=3.990000000000001; %密钥敏感性测试 10^-15
%u=3.99;%密钥：Logistic参数μ
% x0=0.7067000000000001; %密钥敏感性测试 10^-16
x0=0.5475; %密钥：Logistic初值x0
% x0=0.3462; %home图片
p=zeros(1,SUM+1000);
p(1)=x0;
for i=1:SUM+999 %进行SUM+999次循环，产生SUM+1000个数据
p(i+1)=u*p(i)*(1-p(i));
end
p=p(1001:length(p));

%% 3.将p序列变换到0~255范围内整数，转换成M*N的二维矩阵R
p=mod(round(p*10^4),256);
R=reshape(p,N,M)'; %转成M行N列

%% 4.求解混沌方程
%求四个初值X0,Y0,Z0,H0
r=(M/t)*(N/t);
% X0=0.5008000000000001; %密钥敏感性测试
X0=0.4953;
Y0=0.4265;
Z0=0.6928;
H0=0.7803;
% X0=0.5056; %home图片
% Y0=0.505;
% Z0=0.4564;
% H0=0.3062;
A=chen_output(X0,Y0,Z0,H0,r);
X=A(:,1);
X=X(3002:length(X));
Y=A(:,2);
Y=Y(3002:length(Y));
Z=A(:,3);
Z=Z(3002:length(Z));
H=A(:,4);
H=H(3002:length(H));

%% 5.DNA编码
%X,Y分别决定I和R的DNA编码方式，有8种，1~8
X=mod(round(X*10^4),8)+1;
Y=mod(round(Y*10^4),8)+1;
Z=mod(round(Z*10^4),4);
Z(Z==0)=4; %加减法互换
Z(Z==1)=0;
Z(Z==4)=1;
H=mod(round(H*10^4),8)+1;
e=N/t;
for i=r:-1:2
Q1_R=DNA_bian(fenkuai(t,I1,i),H(i));
Q1_G=DNA_bian(fenkuai(t,I2,i),H(i));
Q1_B=DNA_bian(fenkuai(t,I3,i),H(i));

Q1_last_R=DNA_bian(fenkuai(t,I1,i-1),H(i-1));
Q1_last_G=DNA_bian(fenkuai(t,I2,i-1),H(i-1));
Q1_last_B=DNA_bian(fenkuai(t,I3,i-1),H(i-1));

Q2_R=DNA_yunsuan(Q1_R,Q1_last_R,Z(i)); %扩散前
Q2_G=DNA_yunsuan(Q1_G,Q1_last_G,Z(i));
Q2_B=DNA_yunsuan(Q1_B,Q1_last_B,Z(i));

Q3=DNA_bian(fenkuai(t,R,i),Y(i));

Q4_R=DNA_yunsuan(Q2_R,Q3,Z(i));
Q4_G=DNA_yunsuan(Q2_G,Q3,Z(i));
Q4_B=DNA_yunsuan(Q2_B,Q3,Z(i));

xx=floor(i/e)+1;
yy=mod(i,e);
if yy==0
xx=xx-1;
yy=e;
end
I1((xx-1)*t+1:xx*t,(yy-1)*t+1:yy*t)=DNA_jie(Q4_R,X(i));
I2((xx-1)*t+1:xx*t,(yy-1)*t+1:yy*t)=DNA_jie(Q4_G,X(i));
I3((xx-1)*t+1:xx*t,(yy-1)*t+1:yy*t)=DNA_jie(Q4_B,X(i));
end
Q5_R=DNA_bian(fenkuai(t,I1,1),H(1));
Q5_G=DNA_bian(fenkuai(t,I2,1),H(1));
Q5_B=DNA_bian(fenkuai(t,I3,1),H(1));

Q6=DNA_bian(fenkuai(t,R,1),Y(1));

Q7_R=DNA_yunsuan(Q5_R,Q6,Z(1));
Q7_G=DNA_yunsuan(Q5_G,Q6,Z(1));
Q7_B=DNA_yunsuan(Q5_B,Q6,Z(1));

I1(1:t,1:t)=DNA_jie(Q7_R,X(1));
I2(1:t,1:t)=DNA_jie(Q7_G,X(1));
I3(1:t,1:t)=DNA_jie(Q7_B,X(1));

Q_jiemi(:,:,1)=uint8(I1);
Q_jiemi(:,:,2)=uint8(I2);
Q_jiemi(:,:,3)=uint8(I3);

%% 6、去除加密时补的零
M1=0; %加密时补零的参数，M1=mod(M,t);作为密钥
N1=0; %加密时补零的参数，N1=mod(N,t);作为密钥
if M1~=0
Q_jiemi=Q_jiemi(1:M-t+M1,:,:);
end
if N1~=0
Q_jiemi=Q_jiemi(:,1:N-t+N1,:);
end

figure;imhist(Q_jiemi(:,:,1));
figure;imhist(Q_jiemi(:,:,2));
figure;imhist(Q_jiemi(:,:,3));

%比较解密后的图与原图是否完全相同
%II=imread('../原始、加密、解密图片/lena.png','png');
%cha=sum(sum(sum(Q_jiemi-II))); %两幅图做差后求总和
%% 保存图片

imwrite(Q_jiemi,'../原始、加密、解密图片/解密后的lena.png','png');
disp('您输入的解密密钥为：');
disp(['密钥1：μ=',num2str(u),' 密钥2：x0=',num2str(x0),' 密钥3：x(0)=',num2str(X0),' 密钥4：y(0)=',num2str(Y0),' 密钥5：z(0)=',num2str(Z0),]);
disp(['密钥6：h(0)=',num2str(H0),' 密钥7：M1=',num2str(M1),' 密钥8：N1=',num2str(N1),' 密钥9：xx0=',num2str(xx0),' 密钥10：xx1=',num2str(xx1)]);
disp('解密完成');
figure;imshow(Q_jiemi);
%title('解密后图片');