BoT-SORT: Robust Associations Multi-Pedestrian Tracking—鲁棒的关联多行人跟踪

BoT-SORT: Robust Associations Multi-Pedestrian Tracking

class TrackState(object):
    New = 0
    Tracked = 1
    Lost = 2
    LongLost = 3
    Removed = 4

论文概览

首先结合相关的知识对整个的BoT-SORT算法进行概览，发表于2022年的BoT-SORT多目标跟踪算法引起我关注的地方主要是其在MOT17和MOT20挑战赛上取得了最高的分数，其二该算法是在ByteTrack的基础上改进的，同时也保留了低分框和高分框的一个思想。第三是它同时提供了带有reid网络的版本。

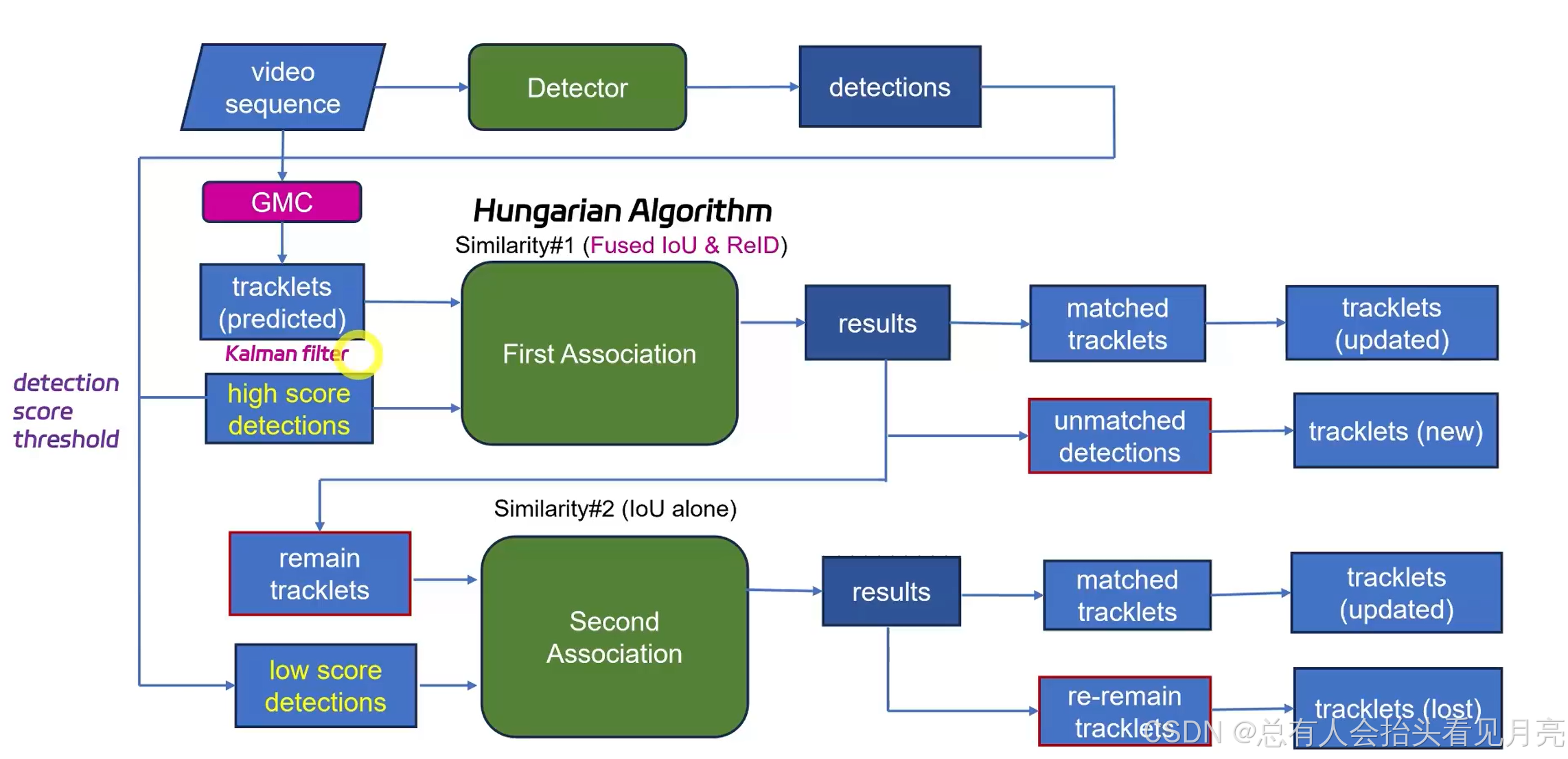
论文中提供了整个算法的一个流程图如下所示。

这里的深度外观提取器可以采用SBS-S50，同时开始的图像这里可以使用相机的补偿。关联的时候采用融合的iou和reid特征来进行。最后提供了一个可选的后处理。

一种新的多目标跟踪器BoT-SORT，它结合了运动和外观信息、相机运动补偿和更准确的卡尔曼滤波状态向量。

论文中提到的三个改进点主要是：

1. Kaman滤波器：使用离散Kalman滤波器来建模图像平面中物体的运动，采用常速度模型，使用更准确的状态向量。

2. 相机运动补偿：通过相机运动补偿来纠正相机运动对目标跟踪的影响，提高跟踪的准确性。

3. IoU和ReID的余弦距离融合：提出了一种新的简单但有效的方法，用于loU和ReID的余弦距离融合，以更稳健地关联检测和轨迹。

通过将这些改进集成到ByteTrack中，提出了两个新的最先进的跟踪器，BoT-SORT和BoT-SORT-ReID。这里是有涉及到reid版本的。

这里补充的第一个概念CMC相机运动补偿。

相机运动补偿（Camera Motion Compensation，CMC）是一种在视频分析中常用的技术，特别是在多目标跟踪（Multi-Object Tracking，MOT）领域。它主要指的是在视频序列中，由于相机自身的运动（如平移、旋转等）导致图像中的目标位置发生变化时，通过估计相机的运动并相应地调整图像中的目标位置，以补偿相机运动带来的影响 。

• 计算图像背景的特征点，如角点检测。
• 对上一帧与当前帧进行光流匹配，以估计相机运动。
• 根据特征点计算旋转和平移参数，然后使用这些参数来补偿预测的边界框位置。

卡尔曼滤波的改进:

通过改进卡尔曼滤波的形式，来对卡尔曼滤波器来进行改进。

在deepsort中的状态向量也就是我们所熟悉的八元组的形式。

$$x={\left[xc,yc,a,h,x{c}^{\prime },yc{,}^{\prime }{a}^{\prime },s^{\prime }\right]}^{\top }$$

其中(xc，yc)是图像平面上对象中心点的2D坐标。s是边界框的比例（面积）a是边界框的长宽比。

然而，通过实验发现，直接估计边界框的宽度和高度可以得到更好的性能因此，我们选择如等式（1）中定义KF的状态向量，等式（2）中定义测量向量。

$$\begin{array}{c}{\mathbf{x}}_k=[x_c(k),y_c(k),w(k),h(k),\\ {{\dot{x}}_c(k),{\dot{y}}_c(k),\dot{w}(k),\dot{h}(k)]}^{\top }\\ {\mathbf{z}}_k={\left[z_{x_c}(k),z_{y_c}(k),z_w(k),z_h(k)\right]}^{\top }\end{array}$$

过程的噪声协方差和对应的测量的噪声协方差也会随之发生相应的改变。

$$\begin{array}{l}\begin{array}{rl}{\mathbf{Q}}_k=\mathrm{diag}& ({\left({\sigma }_p{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_p{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_p{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_p{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_v{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_v{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_v{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_v{\hat{h}}_{k-1\mid k-1}\right)}^2)\end{array}\\ \begin{array}{r}{\mathbf{R}}_k=\mathrm{diag}({\left({\sigma }_m{\hat{w}}_{k\mid k-1}\right)}^2,{\left({\sigma }_m{\hat{h}}_{k\mid k-1}\right)}^2,\\ {\left({\sigma }_m{\hat{w}}_{k\mid k-1}\right)}^2,{\left({\sigma }_m{\hat{h}}_{k\mid k-1}\right)}^2)\end{array}\end{array}$$

摘要概括

这一篇文章的摘要十分的简单，主要就包括了两个方面，第一提出了自己改进的三个创新点，第二介绍在挑战赛中排名第一。

1. 结合了运动motion和外观appearance信息的优势，加入了相机运动补偿，以及更准确的卡尔曼滤波状态向量。
2. 我们的新跟踪器 BoT-SORT 和 BoT-SORT-ReID 在 MOTchallenge 数据集中排名第一。

引言与相关工作

• 大多数类SORT算法都采用以恒速模型假设的卡尔曼滤波器作为运动模型。
• 最近的大多数方法都使用经典跟踪器 DeepSORT 中提出的 KF 状态进行表征它尝试估计框的长宽比而不是宽度，这会导致宽度尺寸估计不准确。
• 使用 IoU 通常可以实现更好的 MOTA，而 Re-ID 可以实现更高的 IDF1。

对于每个贡献的主要的作用进行了一下简单的总结：例如基于相机运动补偿的特征跟踪器和合适的卡尔曼滤波器状态向量以实现更好的框定位。新的简单而有效的 IoU 和 ReID 余弦距离融合方法，以实现检测和轨迹之间更强大的关联。

相关的工作中则简单的提到了之前的一些方法：

1. 在StrongSORT中的ECC相机运动补偿。和最大化或匹配特征（例如ORB）的图像配准来对齐帧。

2. 在拥挤和人群遮挡的情况下基于外观的重识别的效果较差。

3. 放弃了外观信息并不是说完全的放弃，仅依靠高性能检测器和运动信息来实现高运行速度和最先进的性能。 特别是 ByteTrack ，它通过匹配高置信度检测然后与低置信度检测进行另一个关联来利用低分检测框。

核心方法

在核心方法的部分，我们分别对BoT-SORT算法中的三个主要的方面依次的进行细化和解释。

通过将这些集成到著名的 ByteTrack跟踪器中，我们提出了两种新的最先进的跟踪器分别是

• BoT-SORT
• BoT-SORT-ReID

卡尔曼滤波状态的改进

1. 在SORT算法中状态向量被设置为7元组的形式‘

• （Xc,Yc）:图像平面中物体中心的 2D 坐标
• s:是边界框比例（面积）
• a:是边界框长宽比

2. 在最近的追踪器中，状态向量已更改为八元组。例如DeepSort但是我们通过实验发现，直接估计边界框的宽度和高度可以获得更好的性能

因此，使用 Q 和 R 的选择会产生与时间相关的 Qk 和 Rk。 随着我们对 KF 状态向量的更改，过程噪声协方差 Qk 和测量噪声协方差 Rk 矩阵也被修改。对于论文中提到的Qk和Rk为啥会与时间相关并且随输入状态的改变为改变还没太理解。

$$\begin{array}{c}{\mathbf{x}}_k=[x_c(k),y_c(k),w(k),h(k),\\ {{\dot{x}}_c(k),{\dot{y}}_c(k),\dot{w}(k),\dot{h}(k)]}^{\top }\\ {\mathbf{z}}_k={\left[z_{x_c}(k),z_{y_c}(k),z_w(k),z_h(k)\right]}^{\top }\end{array}$$

过程的噪声协方差和对应的测量的噪声协方差也会随之发生相应的改变。DeepSORT提出过程噪音协方差Q以及测量噪音协方差R要以预测变量和测量变量为函数，所以这里的Q、R是时变的Qk、 Rk根据我们略微不同的变量x修改了Q和R

$$\text{ 设 }{\sigma }_p=0.05,{\sigma }_v=0.00625,{\sigma }_m=0.05\text{ 。 }$$

$$\begin{array}{l}\begin{array}{rl}{\mathbf{Q}}_k=\mathrm{diag}& ({\left({\sigma }_p{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_p{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_p{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_p{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_v{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_v{\hat{h}}_{k-1\mid k-1}\right)}^2,\\ & {\left({\sigma }_v{\hat{w}}_{k-1\mid k-1}\right)}^2,{\left({\sigma }_v{\hat{h}}_{k-1\mid k-1}\right)}^2)\end{array}\\ \begin{array}{r}{\mathbf{R}}_k=\mathrm{diag}({\left({\sigma }_m{\hat{w}}_{k\mid k-1}\right)}^2,{\left({\sigma }_m{\hat{h}}_{k\mid k-1}\right)}^2,\\ {\left({\sigma }_m{\hat{w}}_{k\mid k-1}\right)}^2,{\left({\sigma }_m{\hat{h}}_{k\mid k-1}\right)}^2)\end{array}\end{array}$$

这种修改的好处就是：可以提高HOTA的值：假设对 KF 的修改有助于改善边界框宽度与对象的拟合。

广泛使用的卡尔曼滤波器（蓝色虚线）和建议的卡尔曼滤波器（绿色）。 看来所提出的 KF 产生的边界框宽度更准确地适合对象。

相机运动补偿的改进

在动态相机情况下，图像平面中的边界框位置可能会发生巨大变化，这可能会导致 ID 切换或漏报增加本质上是由于相机本身的一些参数的影响

1. 我们遵循 OpenCV 视频稳定实现中使用的全局运动补偿 (GMC) 技术。通过仿射变换实现视频稳定模块（通过SIFT或者稀疏光流等一些方法包括了从文件中读取例如我之前看的StrongSORT中的ECC）

2. 为了将预测边界框从帧 k - 1 的坐标系变换到下一帧 k 的坐标，使用计算出的仿射矩阵 Ak k-1 ，如下所述。

$${\mathbf{A}}_{k-1}^k=\left[{\mathbf{M}}_{2x2}\mid {\mathbf{T}}_{2x1}\right]=\left[\begin{array}{lll}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right]$$

首先论文中提到了A矩阵是一个仿射矩阵是一个2x3的矩阵。包括了两部分组成M是2x2的矩阵和T是2x1的矩阵

• M包含了尺度和旋转的操作。
• T主要是包含了平移的操作。

其实意思就是将经过运动补偿之后的xk和pk在带入到之后的卡尔曼滤波的更新过程公式中进行计算求解

$${\mathbf{A}}_{k-1}^k=\left[{\mathbf{M}}_{2x2}\mid {\mathbf{T}}_{2x1}\right]=\left[\begin{array}{lll}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right]$$

$${\tilde{\mathbf{M}}}_{k-1}^k=\left[\begin{array}{cccc}\mathbf{M}& 0& 0& 0\\ 0& \mathbf{M}& 0& 0\\ 0& 0& \mathbf{M}& 0\\ 0& 0& 0& \mathbf{M}\end{array}\right],{\tilde{\mathbf{T}}}_{k-1}^k=\left[\begin{array}{c}{a}_{13}\\ a_{23}\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]$$

$$\begin{array}{c}{\hat{\mathbf{x}}}_{k\mid k-1}^{\prime }={\tilde{\mathbf{M}}}_{k-1}^k{\hat{\mathbf{x}}}_{k\mid k-1}+{\tilde{\mathbf{T}}}_{k-1}^k\\ {\mathbf{P}}_{k\mid k-1}^{\prime }={\tilde{\mathbf{M}}}_{k-1}^k{\mathbf{P}}_{k\mid k-1}{\tilde{\mathbf{M}}}_{k-1}^{k^{\top }}\end{array}$$

补偿完成之后在带入到卡尔曼滤波的更新公式中进行计算。

$$\begin{array}{l}{\mathbf{K}}_{\mathbf{k}}={\mathbf{P}}_{k\mid k-1}^{\prime }{\mathbf{H}}_k^{\top }{\left({\mathbf{H}}_k{\mathbf{P}}_{k\mid k-1}^{\prime }{\mathbf{H}}_k^{\top }+{\mathbf{R}}_k\right)}^{-1}\\ {\hat{\mathbf{x}}}_{k\mid k}={\hat{\mathbf{x}}}_{k\mid k-1}^{\prime }+{\mathbf{K}}_k\left({\mathbf{z}}_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_{k\mid k-1}^{\prime }\right)\\ {\mathbf{P}}_{k\mid k}=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k\mid k-1}^{\prime }\end{array}$$

通过应用这种方法，我们的跟踪器对相机运动变得鲁棒。

IoU - Re-ID融合上的改进

1. 采用指数移动平均（EMA）机制来更新匹配的轨迹外观状态。第k帧处的第i个轨迹表示如下所示： 利用指数移动平均来平衡过去和当前的外观特征。

$$e_i^k=\alpha e_i^{k-1}+(1-\alpha )f_i^k$$

• 其中 fk i 是当前匹配检测的外观嵌入α = 0.9

2. 由于外观特征可能容易受到人群、遮挡和模糊物体的影响，为了保持正确的特征向量，我们只考虑高置信度检测。

3. 同时将改进后的运动特征和我们的外观特征之间做一个加权平均：共同加权和来计算成本矩阵 C 这里的λ=0.98

$$C=\lambda A_a+(1-\lambda )A_m$$

4. 一种结合运动和外观信息的新方法，即 IoU 距离矩阵和余弦距离矩阵。

$$\begin{array}{c}{\hat{d}}_{i,j}^{\text{cos }}=\{\begin{array}{l}0.5\cdot d_{i,j}^{\text{cos }},\left(d_{i,j}^{\text{cos }}<{\theta }_{\text{emb }}\right)\wedge \left(d_{i,j}^{\text{iou }}<{\theta }_{\text{iou }}\right)\\ 1,\text{ otherwise }\end{array}\\ C_{i,j}=\min \left\{d_{i,j}^{\text{iou }},{\hat{d}}_{i,j}^{\text{cos }}\right\}\end{array}$$

对于外观和lou都相似的目标，给予更小的cost，否则设为1

融合的改进就是对于余弦距离若是iou距离和余弦距离都小于阈值（0.25 0.5）设置为0.5x余弦距离，否则设置为1。最后成本矩阵取其中的最小值。