【R】【课程笔记】07 分位数回归与VaR（ES）计算

最新推荐文章于 2022-12-24 11:19:14 发布

空明远

最新推荐文章于 2022-12-24 11:19:14 发布

阅读量8.2k

点赞数 26

分类专栏：数据分析 # R

本文链接：https://blog.csdn.net/weixin_46285914/article/details/106359642

版权

数据分析同时被 2 个专栏收录

9 篇文章 14 订阅

订阅专栏

6 篇文章 4 订阅

订阅专栏

本文是课程《数据科学与金融计算》第7章的学习笔记，主要介绍计算VaR/ES风险测度的各种方法和极值理论等，用于知识点总结和代码练习，Q&A为问题及解决方案。

往期回顾：

博文	内容
【R】【课程笔记】01 R软件基础知识	数据类型、数据结构、运算、绘图等
【R】【课程笔记】02+03 基于R软件的计算	聚类分析、因子分析、神经网络、支持向量机等
【R】【课程笔记】04+05 数据预处理+收益率计算	金融数据处理、收益率、R与C++等
【R】【课程笔记】06 金融波动模型	GARCH、SV、高频波动模型等
【R】【课程笔记】07 分位数回归与VaR（ES）计算	VaR、ES、极值模型等
【R】【课程笔记】08 金融投资组合决策分析	均值-方差模型、均值-VaR模型、均值-CVaR模型等

第七章分位数回归与VaR（ES）计算

课程链接：理论篇《金融风险管理》02 金融风险管理基本理论

7.1 VaR与ES的计算

包：
PerformanceAnalytics：风险分析与绩效评价
evir：极值理论与方法
quantreg：分位数回归理论与方法
VGAM：向量广义线性模型和加性模型
splines：样条函数
np：非参数核光滑方法

一、VaR

分位数：对于任何一元随机变量X的累积分布函数F（x）和概率τ（0<τ<1），则称： $x_τ=inf \{x|F(x)≥τ \}$ ，inf(·)表示满足条件的最小实数。
VaR：指一个特定的金融资产或投资组合，在特定的持有期内，在一定的置信水平100（1-τ）%下，面临的最大可能损失。
（1）记金融资产或资产组合损失L的累积分布函数为 $F_L(l)$ ，则置信水平100（1-τ）%时的VaR就是损失分布的第（1-τ）分位数。
（2）以负收益（-R）表示损失，则置信水平100（1-τ）%时的VaR是收益分布的第τ分位数的相反数。

二、ES

ES：对于金融资产损失函数L，在VaR的基础上，给出置信水平100（1-τ）%的ES定义： $ES_{1-τ}(L)=E[L_t|L_t>VaR_{1-τ}(L)]$ ，表示：金融头寸的损失超过VaR条件下的期望损失（或平均损失）。

三、RiskMetrics模型

在这里插入图片描述

注：
$r_t$ 服从一个条件正态分布，条件均值为0，条件方差为 $σ_t^2$ ；
$ε_t$ 服从标准正态分布；
$σ_t^2$ 服从一个无漂移的IGARCH(1,1)模型；
$λ$ 为权重参数，此模型推荐为0.94。

1、计算VaR
思路：根据得到的 $r_t$ 的条件方差 $σ_t^2$ ，向前一步预测，得到 $σ_{t+1}^2$ ，在t时刻下，得到： $r_{t+1}$ 服从条件均值为0，条件方差为 $σ_{t+1}^2$ 的条件正态分布。令τ为上尾概率，则在t时刻可以计算出持有期为1天的VaR。
$z_{1-τ}$ 为标准正态分布的（1-τ）分位数。
在这里插入图片描述
当持有期为l天时，从t+1天到t+l天的对数收益率为 $r_t[l]$ （求和），则 $r_t[l]$ 服从条件均值为0，条件方差为 $σ_{t}^2[l]$ 的条件正态分布。

进一步得出， $r_t[l]$ 服从条件均值为0，条件方差为 $σ_{t}^2[l]=l*σ_{t+1}^2$ 的条件正态分布。令 $τ$ 为上尾概率，在t时刻可以计算出持有期为 $l$ 天的VaR为：在这里插入图片描述
即：RiskMetrics模型的时间平方根法则。

2、ES计算：

持有期为1天和l天的ES计算
小实验：积分验证（integrate）

f1=function(x)
{
  x*dnorm(x)
}
integrate(f1,1.645,100)$value

dnorm(1.645)

例1：用R软件求出多头头寸持有期为1天和5天的VaR和ES（IGARCH）
函数：ugarchspec：拟合一元GARCH模型
固定不用估计的参数： fixed.pars=list(omega=0,alpha1=0.06)

price.AAPL <- AAPL$AAPL.Adjusted
R <- 100*diff(log(price.AAPL))                                   
r <- (-1)*R[-1]        # 删掉第一个空值，负收益即损失

library(rugarch)                                            
spec1 = ugarchspec(variance.model=list(model="iGARCH", garchOrder=c(1,1)), 
                   mean.model=list(armaOrder=c(0,0), include.mean=FALSE), 
                   distribution.model="norm", fixed.pars=list(omega=0,alpha1=0.06))        

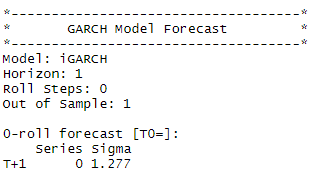
forecast1 <- ugarchforecast(spec1, data=r,n.roll=0,n.ahead=1,out.sample=1) 

forecast1
VaR1 <- qnorm(0.95)*1.277
ES1 <- dnorm(qnorm(0.95))*1.277/0.05
VaR5 <- qnorm(0.95)*1.277*sqrt(5)
ES5 <- dnorm(qnorm(0.95))*1.278*sqrt(5)/0.05

在这里插入图片描述

四、GARCH模型与VaR和ES计算

ARMA-GARCH模型

1、基于GARCH模型的VaR计算
持有期为1天的VaR（误差项ε服从正态分布或t分布）

2、基于GARCH模型的ES计算
持有期为1天的ES（误差项ε服从正态分布或t分布）
例2：用R软件求出多头头寸持有期为1天和5天的VaR和ES（ARMA-GARCH）
包：fGarch，函数：garchFit

library(fGarch)
# 持有期1天
m1 <- garchFit(formula = ~arma(0,0)+garch(1,1), data = r, cond.dist = c("norm"), trace = FALSE)
summary(m1)
p1 <- predict(m1,n.ahead=1)  
VaR <- p1$meanForecast+p1$standardDeviation*qnorm(0.95)
ES <- p1$meanForecast+p1$standardDeviation*dnorm(qnorm(0.95))/(1-0.95)

# 持有期5天
m2 <- garchFit(formula = ~arma(1,1)+garch(1,1), data = r, cond.dist = c("norm"), trace = FALSE)
p2 <- predict(m2,n.ahead=5)
VaR <- p2$meanForecast[5]+p2$standardDeviation[5]*qnorm(0.95)
ES <- p2$meanForecast[5]+p2$standardDeviation[5]*dnorm(qnorm(0.95))/(1-0.95)

#t分布
m3 <- garchFit(formula = ~arma(0,0)+garch(1,1), data = r, cond.dist = c("std"), trace = FALSE)
summary(m3)
p3 <- predict(m3,n.ahead=1)
VaR <- p3$meanForecast+p3$standardDeviation*qt(0.95,5)/sqrt(5/3)
ES <- p3$meanForecast+p3$standardDeviation*dt(qt(0.95,5)/sqrt(5/3),5)/(1-0.95)

7.2 分位数回归与VaR（ES）计算

分位数回归（QR）：揭示响应变量整个条件分布特征，应用条件更为宽松。

一、线性分位数回归

设Y为一元随机变量，其右连续分布函数为 $F (y) = P r (Y \leq y)$ ，则对任意0<τ<1有：
$F^{-1}(τ)=inf\{y|F(y)≥τ\}$
注： $F^{-1}（τ）$ 为 $Y$ 的第 $τ$ 分位数

分位数产生于最优化问题：求分布函数为F（·）的一元随机变量的点估计，分位数可以看作是最优化问题的解，进一步推广到估计条件分位数模型。
在这里插入图片描述
线性分位数回归的检验方法主要有：Wald检验、秩检验（求回归参数估计的置信区间）、似然比检验。

例4：用线性分位数回归进行参数估计
包：quantmod

#例7.4
library(quantreg)                  
fit1 <- rq(formula = r.price ~ r.volume, tau = 0.5, data = SSEC)    # 分位数回归拟合
fit1                             

plot(r.volume, r.price, xlab= "volume", ylab="price", type = "n") 
points(r.volume, r.price, col= "blue")
abline(lm( r.price ~ r.volume), lty=1, lwd=2) #线性回归
abline(rq( r.price ~ r.volume), lty=2, lwd=2) #分位数回归
taus <- c( 0.05, 0.1, 0.25, 0.75, 0.9, 0.95) # 不同取值
for(i in 1:length(taus)){
  abline(rq(r.price ~ r.volume, tau=taus[i]), lty=3)
}

#例7.5
summary(fit2, se = "rank")  # 包含置信区间，秩检验

#例7.6
#预测
fp <- predict.rq(fit1, newdata= data.frame(r.volume))
fp

二、非线性分位数回归

参数非线性分位数回归：
Box-Cox变换分位数回归（最常用）
局部多项式分位数回归
B样条分位数回归

1、Box-Cox变换分位数回归
“数据不是正态，所以没法用正态性质，所以每个点都做一个变换。”

LMS方法：对于解释变量x的给定值，对响应变量y运用正态Box-Cox变换，选择三个参数使惩罚对数似然函数最大化，那么可以通过Box-Cox变换转化为正态分布的适当分位数获得所需的分位数。
在这里插入图片描述
关键在于计算三个参数。通过极大化一个惩罚的对数似然函数来估计三个参数，这个惩罚的对数似然函数为：

例7：运用正态Box-Cox变换分位数回归进行拟合
包：VGAM ，命令：lms.bcn：进行正态Box-Cox变换分位数回归
解释变量：日对数收益率，响应变量：日交易量
注：s()表示光滑

#例7.7
library(VGAM) 
# s()表示光滑，变成两项f=f1+f2，4：截距项+线性+二次+三次，2：截距项+线性
fit <- vgam(r.volume ~ s(r.price, df= c(4,2)), lms.bcn(zero=1), SSECdata)
head(predict(fit))
head(fitted(fit))
head(cdf(fit))  
par(bty = "l", mar = c(5, 4, 4,3) + 0.1, xpd = TRUE)
qtplot(fit, percentiles = c(5, 25, 75, 95), main='分位数', 
       las = 1, xlab='价格', ylab='交易量', lwd = 2, lcol = 4)

2、局部多项式分位数回归
（1）函数未知，用多项式近似。
（2）若要光滑，窗宽h取大一点。在这里插入图片描述

注：K为一正的、对称的单峰函数，h为带宽参数。在解释变量 $x_i=x$ 处，响应变量y在τ分位点处的条件分位数 $Q_τ(y|x)$ 的估计值就是 $β_0$

包：lprq：局部多项式回归

#例7.8
taus <- c(0.05,0.50,0.95)  #设定分位点
for(i in 1:length(taus)){
  tau = taus[i]
  fit <- lprq(price,volume,h=10,tau)
  lines(fit$xx,fit$fv,lty=i)
}                 # 绘制局部多项式分位数回归拟合图

3、B样条分位数回归
使用B样条基函数平滑非线性函数，转换为最小二乘法计算。
在这里插入图片描述
先得到参数向量的估计，再得到非线性函数的估计。

非参数非线性分位数回归
核估计：用其周围数据的加权平均和，关键在于权重如何去选
Nadaraya-Watson核估计：主要利用非参数密度估计的思想，直接对未知形式的回归函数进行估计，可以将其应用到分位数回归中。

令X表示响应变量，Y表示解释变量，令F（y|x）表示在给定X=x时Y的条件分布函数，可以得到F（y|x）的估计：
在这里插入图片描述

例9：包：np，使用npcdistbw命令计算带宽，使用npqreg命令进行核分位数回归。

#例7.9
library(np)
data("Italy")
attach(Italy)
bw <- npcdistbw(formula=gdp~ordered(year))    # 带宽
model.q0.25 <- npqreg(bws=bw, tau=0.25)       # 计算分位数
model.q0.50 <- npqreg(bws=bw, tau=0.50)
model.q0.75 <- npqreg(bws=bw, tau=0.75)
plot(ordered(year), gdp, xlab="year", ylab="GDP λ")     
lines(ordered(year), model.q0.25$quantile, col="red", lty=2)
lines(ordered(year), model.q0.50$quantile, col="blue", lty=3)
lines(ordered(year), model.q0.75$quantile, col="red", lty=2)
legend(ordered(1951), 32, c("tau = 0.25", "tau = 0.50", "tau = 0.75"), 
       lty=c(2, 3, 2), col=c("red", "blue", "red"))
detach(Italy)

三、基于分位数回归的VaR和ES计算

y：金融资产的收益，x：影响金融资产收益的解释变量
在这里插入图片描述
进一步得到，VaR和ES的计算公式

例10：基于历史数据做预测，求VaR

#例7.10
library(quantreg)
fit <- rq(r0 ~ ., tau = 0.05, data=re)
fit

ree <- re[2761:2764,]
fp <- predict(fit, newdata = ree)
fp
VaR <- -fp
VaR

7.3 VaR(ES)的极值方法

一、区间极大值模型（BMM模型）

1、广义极值分布（Weibull、Frechet、Gumbel）：GEV分布
在这里插入图片描述

#图7.7

x <- seq(-10, 10, by=0.1)       
library(evir)
Gumbel_density <- exp(-x-exp(-x))    # 双指数分布
Weibull_density <- dgev(x, xi = -0.3, mu = 0, sigma = 1)
Frechet_density <- dgev(x, xi = 0.8, mu = 0, sigma = 1)

plot(c(x,x,x), c(Gumbel_density,Weibull_density,Frechet_density),   
     type='n', xlab='x', ylab='密度',las=1)
lines(x, Gumbel_density, type='l', lty=1, col='black')
lines(x, Weibull_density, type='l', lty=2, col='blue')
lines(x, Frechet_density, type='l', lty=3, col='red')
legend('topright', legend=c('Gumbel','Weibull','Frechet'), lty=c(1,2,3), col=c('black','blue','red'))

2、BMM模型参数估计

参数方法：极大似然估计（MLE）
非参数方法：Hill估计，仅对Frechet分布适用，即当形状参数大于0才可用于估计。在大部分情况下，金融时间序列都是尖峰厚尾的，符合Frechet分布的特征。
在这里插入图片描述
3、基于BMM模型的VaR计算
根据极值分布分位数和原数据分位数的关系：

4、基于BMM模型的ES计算

#例7.11
m1 <- gev(r, block=21)        
m1
names(m1)
xi <- as.numeric(m1$par.ests[1])
xi
sigma <- as.numeric(m1$par.ests[2])
sigma
mu <- as.numeric(m1$par.ests[3])
mu
VaR <- mu-(sigma/xi)*(1-(-21*log(1-0.05))^(-xi))
VaR
VaR5 <- 5^(xi)*VaR 
VaR5

#例7.12
Hill <- function(r, H){
  # r: 数据
  # H: 次序统计量个数
  r <- as.numeric(r)
  s <- sort(r)
  TT <- length(r)
  ist <- TT - H
  y <- log(s[ist:TT])
  hill <- sum(y[2:length(y)])/H
  hill <- hill - y[1]
  sd <- sqrt(hill^2/H)
  cat('Hill estimate & std-err:', c(hill, sd), '\n')
  return(data.frame(hill=hill, sd=sd))
}
Hill(r,290)
Hill(r,300)
Hill(r,310)

二、阈值模型（POT模型）

1、广义帕累托分布（GDP分布）
（1）超量分布函数
在这里插入图片描述
（2）广义帕累托分布

2、阈值选取
（1）超过阈值u的平均超出量函数

（2）样本超出量函数

3、基于POT模型的VaR计算

4、基于POT模型的ES计算

#例7.13
library(evir)
meplot(r, las=1)                # 画出样本平均超出水平

#图7.9

m1 <- gpd(r, threshold=3.00)    # 拟合广义帕累托模型
m1
par(mfcol=c(2,2))
plot(m1)                        
shape(r,end=1500)               
#例7.14

m2 <- pot(r, threshold=3.00)    
riskmeasures(m2,c(0.95,0.99))