高数 | 【无穷级数】等价无穷小（Talor展开）判敛法 & 交错级数不能用通项等价关系审敛

一、引例

 我们知道，对于正项级数可以利用所谓的通项等价关系进行审敛，即

废话不多说，看例题 ：

---

 二、经错标零

例题你觉得简单？下面这坑你必踩~

经典的错误，标准的零分~

 关注A选项~

你的做法：

应用性质：在级数中加上或减去有限项后级数的敛散性不变

设从某一项 N 之后，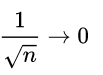

运用等价无穷小

如果按照交错级数审敛法(莱布尼兹审敛法)判断其收敛，故原级数收敛(此处不讨论加绝对值的级数)

但是A说：我才不是 条件收敛！！！

为什么错了呢？

 这里可能就有人会说，我知道我知道！使用等价无穷小判敛法只适用于正项级数。具体证明详见文末。

 回看上面的例子，

蓝色框框里，其实我们是默认了后面的展开也是收敛的。那我们做题肯定不能就这样默认啊╭(╯^╰)╮

应该注意：

• ①等价无穷小如其名，是大小上的等价，而敛散性和大小不存在绝对关系，只可以认为二者大小几乎一致，因为等价无穷小的获得就是将左式的泰勒展开截取主要部分形成的。
• ②“敛散性和大小不存在绝对关系”所包含的关系中有一条关系是确定的：如果其等价无穷小形成的级数的部分和趋于∞，则意味着原无穷级数部分和趋于∞，该级数一定发散

所以我们一定要留一个心眼：展开到你能确定后面都是收敛了的时候。

通过等价无穷小变换和泰勒展开(多去验证几项)其动机应该是 否定原不易直接判断的级数的收敛性的，因为泰勒级数有无穷项，无法全部验证收敛，况且无穷项收敛的级数累加还收敛吗？

再来看一道

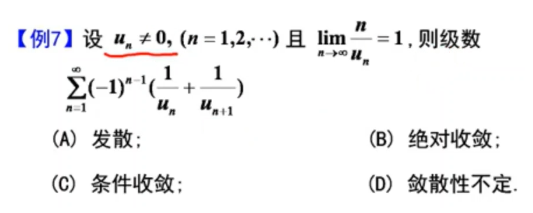
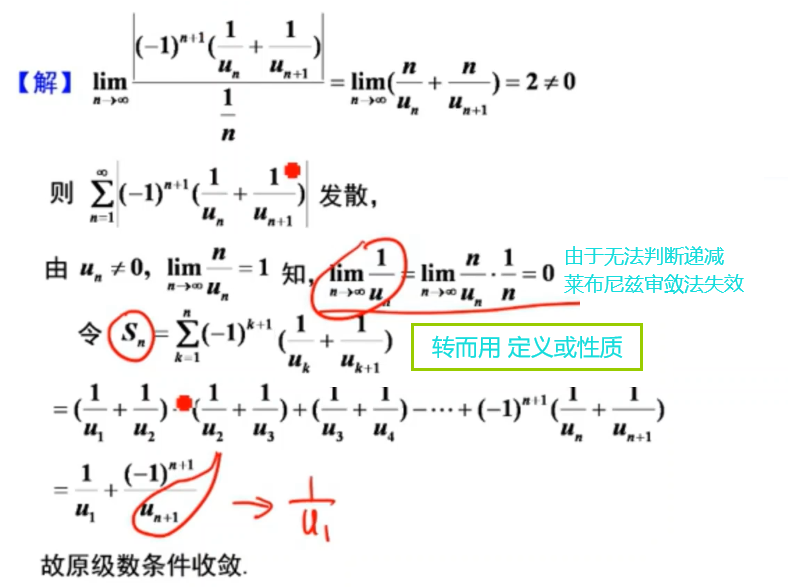
若用等价代换，也是错的！只能用于正项级数！

 欣赏下别的错误解析~

附：别的坑 极限~

三、为什么交错级数不能用通项等价关系审敛

 

 

 

 

有参考~

等价无穷小能应用于判断级数敛散性吗？ - 知乎

交错级数不能用通项等价关系审敛 - 知乎

「进来踩坑」级数判敛的等价法的一个例子_哔哩哔哩_bilibili