1.运动学正解与逆解含义
2.求解肩部的旋转量 γ \gamma γ
在yOz平面内
与实际机器狗的腿部进行对照
下图中直线的实际长度均为在平面yOz中的投影
已知：y，z，h
求解中间量： d ， l ， γ 1 ， γ 2 d，l，\gamma_1，\gamma_2 d，l，γ1，γ2
求解最终量：
γ
\gamma
γ
求解过程：
d
=
y
2
+
z
2
d=\sqrt{y^2+z^2}
d=y2+z2
l
=
d
2
−
h
2
l=\sqrt{d^2-h^2}
l=d2−h2
γ
1
=
−
a
r
c
t
a
n
h
l
\gamma_1=-arctan\frac{h}{l}
γ1=−arctanlh
γ
2
=
−
a
r
c
t
a
n
y
z
\gamma_2=-arctan\frac{y}{z}
γ2=−arctanzy
γ
=
γ
2
−
γ
1
\gamma=\gamma_2-\gamma_1
γ=γ2−γ1
3.求解小腿的旋转量 β \beta β
在xOz平面中
与实际机器狗的腿部进行对照
下图中直线的实际长度均为在平面xOz中的投影
已知：l，ｘ，hl（大腿长度），hu（小腿长度）
求解中间量：n
求解最终量：
β
\beta
β
求解过程：
s = l 2 + x 2 s=\sqrt{l^2+x^2} s=l2+x2
(
h
u
+
n
)
2
+
m
2
=
s
2
(
1
)
(hu+n)^2+m^2=s^2 \quad (1)
(hu+n)2+m2=s2(1)
n
2
+
m
2
=
h
l
2
(
2
)
n^2+m^2=hl^2 \quad(2)
n2+m2=hl2(2)
式(1)减去式(2)
[
(
h
u
+
n
)
2
+
m
2
]
−
(
n
2
+
m
2
)
=
s
2
−
h
l
2
[(hu+n)^2+m^2]-(n^2+m^2)=s^2-hl^2
[(hu+n)2+m2]−(n2+m2)=s2−hl2
2
⋅
h
u
⋅
n
+
h
u
2
=
s
2
−
h
l
2
2 \cdot hu \cdot n + hu^2 = s^2 -hl^2
2⋅hu⋅n+hu2=s2−hl2
n
=
s
2
−
h
l
2
−
h
u
2
2
h
u
n=\frac{s^2-hl^2-hu^2}{2hu}
n=2hus2−hl2−hu2
β
=
−
a
r
c
c
o
s
n
h
l
\beta=-arccos\frac{n}{hl}
β=−arccoshln
4.求解大腿的旋转量 α \alpha α
在xOz平面中
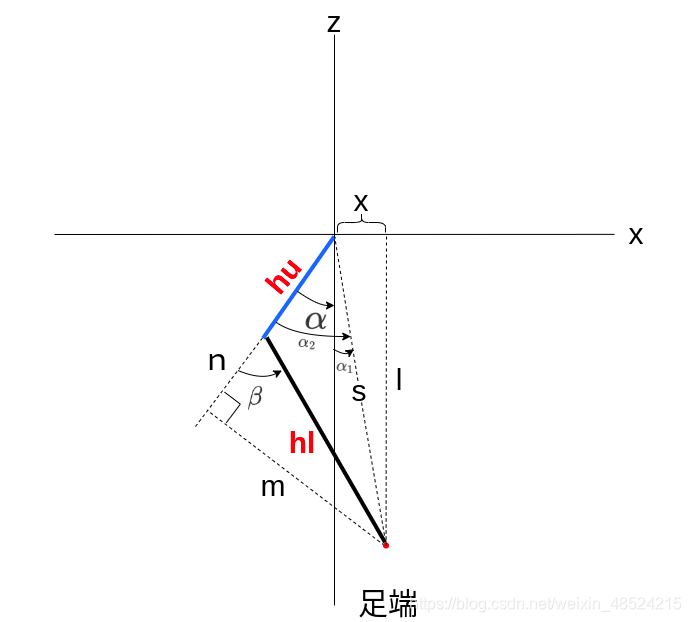
与实际机器狗的腿部进行对照
下图中直线的实际长度均为在平面xOz中的投影
已知：x，l，hu（大腿长度），n，s
求解中间量： α 1 ， α 2 \alpha_1，\alpha_2 α1，α2
求解最终量： α \alpha α
求解过程：
α
1
=
−
a
r
c
t
a
n
x
l
\alpha_1=-arctan\frac{x}{l}
α1=−arctanlx
α
2
=
a
r
c
c
o
s
h
u
+
n
s
\alpha_2=arccos\frac{hu+n}{s}
α2=arccosshu+n
α
=
α
1
+
α
2
\alpha=\alpha_1+\alpha_2
α=α1+α2
扫一扫
2707
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
