PLL锁相环基础知识(一)

最新推荐文章于 2025-03-03 20:03:07 发布

通信射频老兵

最新推荐文章于 2025-03-03 20:03:07 发布

阅读量1.6k

点赞数 23

文章标签： 5G 经验分享射频工程

本文链接：https://blog.csdn.net/weixin_49761275/article/details/145019542

版权

在这里，我们可以看到构成锁相环（PLL）的基本组成部分。在本模块中，你将更深入地了解压控振荡器（VCO）、输出分频器和N分频器，包括整数型和分数型两种类型。

压控振荡器（Voltage Controlled Oscillator，VCO）是锁相环（PLL）的主要组成部分之一。它能在有限的频率范围内产生频率，通常高于参考振荡器的频率。VCO的频率是可调的，通过改变输入调谐电压来控制。这个频率会随着温度、电源电压或半导体工艺的变化而发生较大变化，因此其稳定性远低于参考振荡器。

VCO包含一个谐振电路（或称为振荡电路），可以将其视为电子弹簧。当电容器两端的电压最大时，电感器中的电流最小，反之亦然。假设没有寄生电阻，电路将永远振荡下去。但这怎么可能呢？VCO的谐振电路可以与布谷鸟钟的摆锤相比较。摆锤的长度决定了周期，从而使布谷鸟钟能够保持准确的时间。

为了使摆锤持续摆动，需要以正确的方式施加激励，以保持振荡而不扭曲信号的周期。类似地，LC电路也需要激励。振荡器中的电路损耗，如电感器中的寄生电阻，可能导致电路最终停止振荡。振荡电路电感器的一个衡量指标是品质因数（Quality Factor）或Q值。就像摆锤一样，必须提供一些激励才能使电路持续振荡。

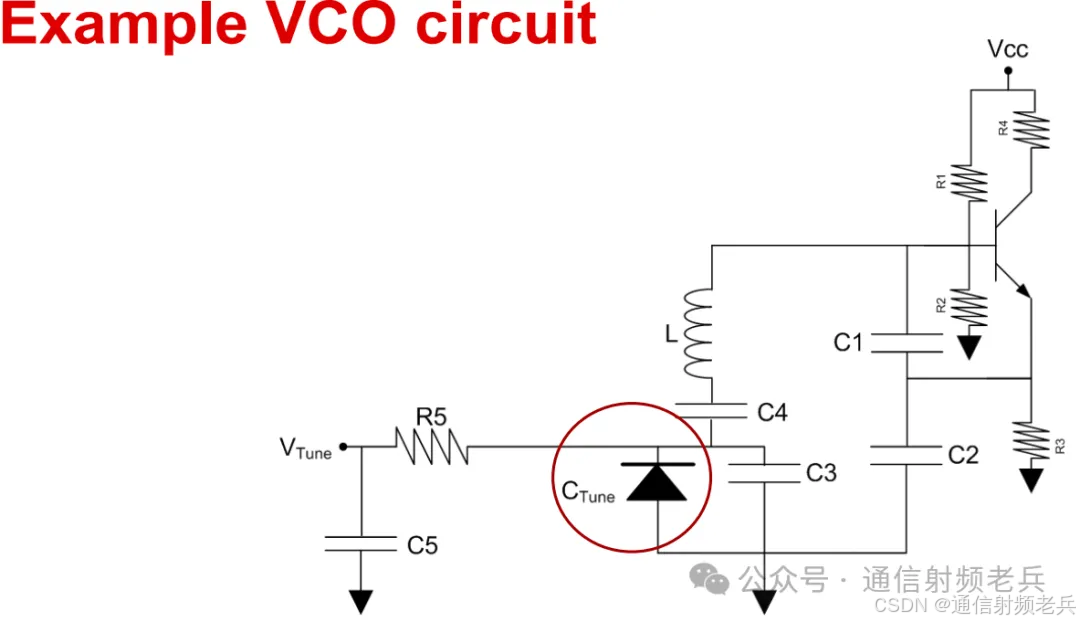
这里我们有一个典型的振荡器电路。当电感电流达到最大值时，电容器两端的电压达到最小值。部分电流流入晶体管并被放大，这会使C1两端的电压增加，从而增加电感顶部的电压。通过这种方式，振荡得以维持。如果C1过大，电路可能会振荡，但有源器件会产生过多的噪声。如果C1过小，则电路可能不够强大，无法维持振荡。

为了实现压控振荡器（VCO）的调谐，通常使用可变电容器——变容二极管。变容二极管的电容通常在皮法拉（Pico farad）范围内，并且随着施加电压的增加而减小。由于这是一个可变电容器，我们希望改变频率的谐振，但又不希望干扰由电容器C1和C2精心设置的反馈。电容器C3增加了变容二极管的电容。C3的值越大，相位噪声越好，但压控振荡器的调谐范围会减小。

电阻器R5将调谐电压与环路滤波器隔离。当压控振荡器（VCO）集成到硅基芯片中时，就会出现一个问题：谐振元件来自哪里？对于电感器，有多种方法。一种方法是在硅基芯片中使用顶层金属层集成螺旋电感器。另一种方法是使用键合线来形成电感。更新的技术允许将更高Q值的谐振器（如体声波谐振器）集成到VCO中。

当VCO集成到硅基芯片中时，通常会使用数字逻辑来切换电容器的接入和断开，以增加调谐范围。VCO的调谐范围可能会因频段而异，并且当接入更多电容时，调谐范围通常会降低。请注意，即使所有电容器都已接入，开关上也会存在电阻，这可能会影响Q值。

通过多组开关电容或电感，可以形成几个不同的频段。通过将压控振荡器（VCO）的调谐范围划分为几个不同的频段，可以在不牺牲相位噪声的情况下增加VCO的调谐范围。这些频段共同覆盖了整个频率范围，但调谐电压和频率之间不再存在一一对应的关系。因此，在进行频率校准时，必须确保在改变VCO频率时选择了正确的频段。

回到锁相环（PLL）架构，需要额外的电路来控制VCO的调谐电压，以将其引导至正确的频率，但为什么需要反馈呢？原因是，即使对于固定的调谐电压，VCO的频率也会随温度、电源电压和工艺的变化而漂移。这就是为什么需要反馈控制环路将VCO的频率锁定到参考频率上的原因。

为了生成这个反馈环路，参考振荡器频率f_osc通过R分频器进行分频，以产生相位检测器频率f_PD。压控振荡器（VCO）的频率f_vco通过N分频器进行分频，以产生反馈信号f_N。如果VCO的频率范围远高于所需频率f_OUT，则可以使用输出分频器将其调整到合适的范围内。

接下来，我们来看看反馈部分，也就是N分频器。N计数器的值是通过将压控振荡器（VCO）的频率除以相位检测器的频率来确定的。该计数器的输入可以是高频信号，因此计数器内部通常会使用预分频器。

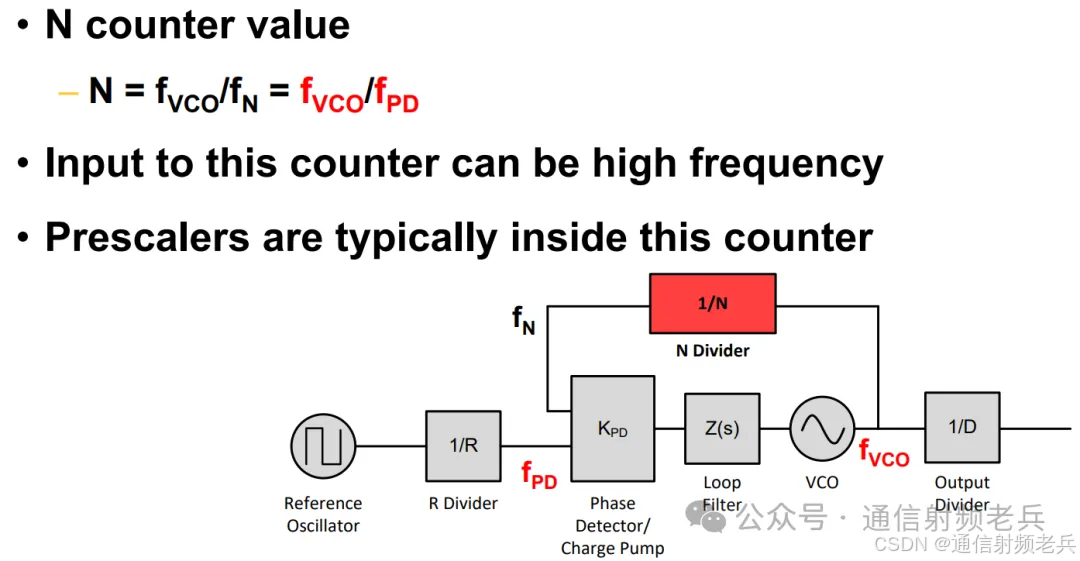
对于非常高的VCO频率，有时仅使用一个固定的预分频器P。P通常是2的幂次方。分频器中的预分频器部分工作在最高频率下，并消耗大部分电流，但N计数器的其余部分工作频率较低，因此可以节省整体电流消耗。

使用预分频器的一个缺点是频率分辨率会降低P倍。一些高频压控振荡器（VCO）具有除以2的输出，该输出可以反馈回锁相环（PLL），其作用与使用预分频器类似。可切换双模预分频器可以在不牺牲分辨率的情况下实现更高的频率分频。

其工作原理是，分频器首先通过预分频器和一个pulse-swallow电路对压控振荡器（VCO）的频率进行分频。每经过P+1个VCO周期，A计数器和B计数器都会减1。当A计数器经过A次（P+1）周期后减至0时，B计数器还剩下B-A个计数，此时pulse-swallow电路被禁用。禁用pulse-swallow电路后，需要再经过(B-A)×P个VCO周期，B计数器才会减至0。

因此，总的N计数为N等于P乘以B加A。在这种架构下，B大于等于A是一个必然结果。如果不满足这个条件，设备将会提前重置并产生错误的分频值。如果N分频器大于已知的最小连续分频比，那么这个B大于等于A的要求总是能够满足的。对于标准的N分频器，这可以通过计算P乘以（P-1）来得出，但其他因素，如分数分频电路，可能会增加这个值。

现在来考虑分数N分频器。在这种情况下，我们想要使用1Mhz的相位检测器频率来生成900.2Mhz的频率。这就需要900又1/5的分数分频。

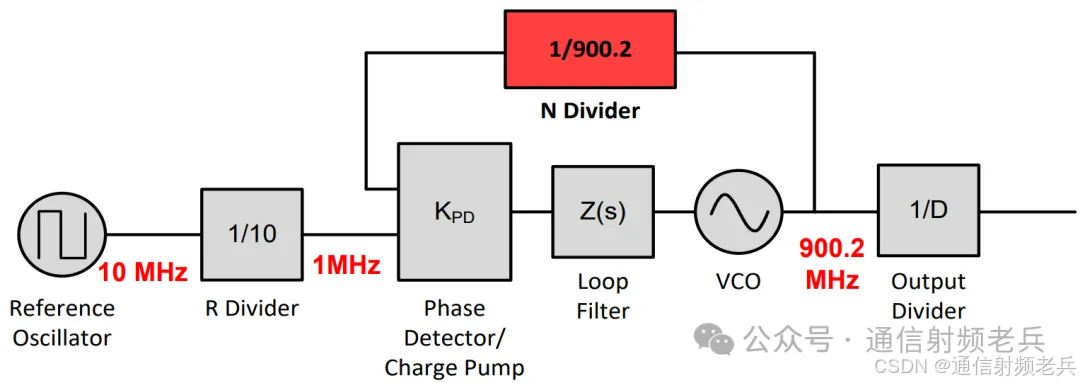
为了实现这一点，我们在900和901之间调制N分频器的值。具体来说，我们使用900作为分频值四次，而使用901作为分频值一次。相位检测器实际上升沿与期望上升沿之间的误差会导致分数杂散，在这种情况下，这些杂散出现在200Khz的倍数处。

通过使N分频器在超过两个值之间进行调制，可以减少分数杂散。这正是高阶德尔塔-西格玛（delta sigma）调制器所采用的方法。在前面的例子中，分数是900.2，一阶调制器会在900和901之间进行调制。二阶调制器可能会使用899、900、901和902这四个值。三阶调制器则可能使用从897到904的范围内的值。调制器并不总是需要使用其范围内的所有数字。分数分频器可以增加最小连续N分频比，因为即使使用调制值，所有值都必须是有效的。