3D坐标入门之——甜甜圈篇

案例效果

WeChat_20220603201218

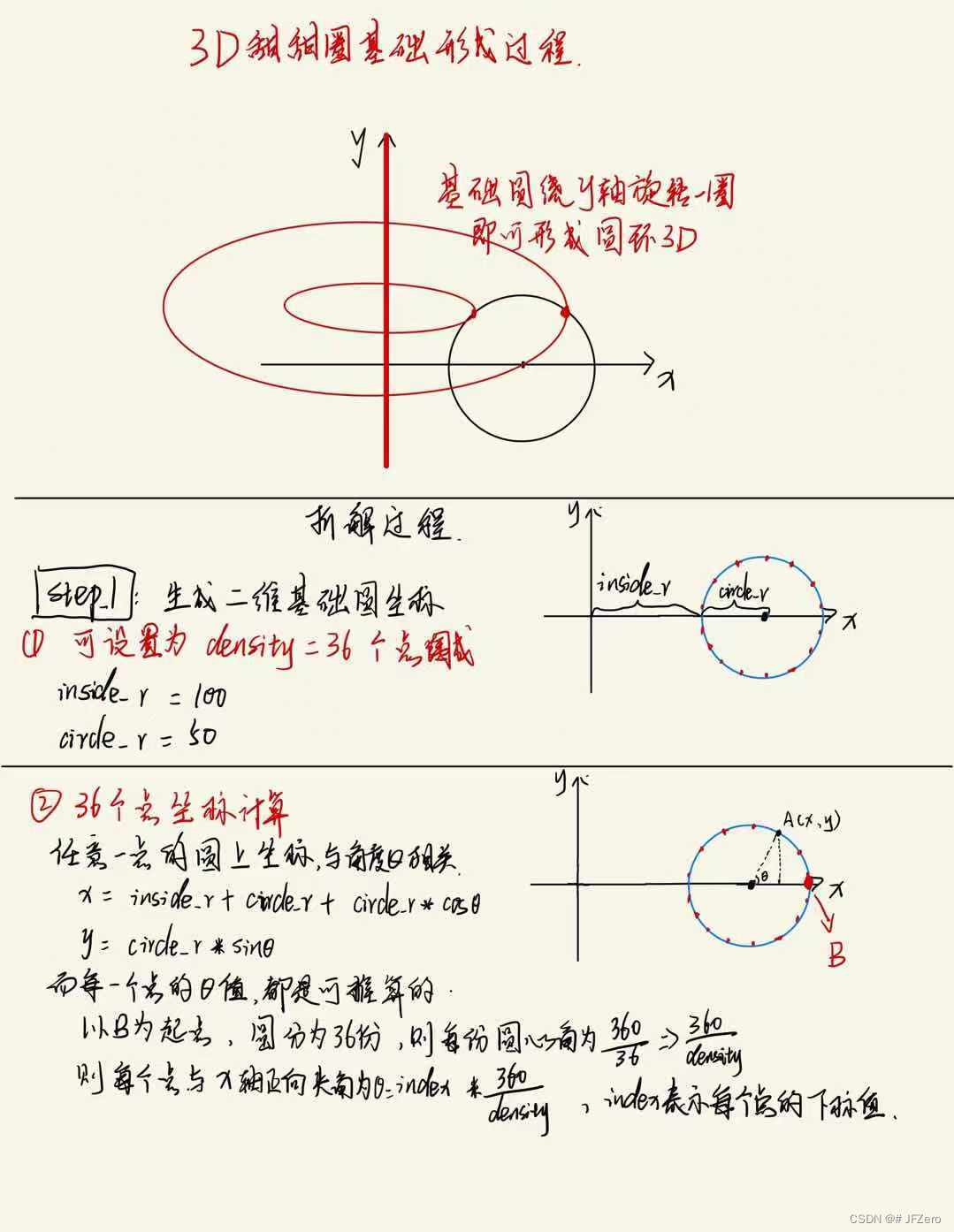
拆解过程

1. 二维基础圆雏形
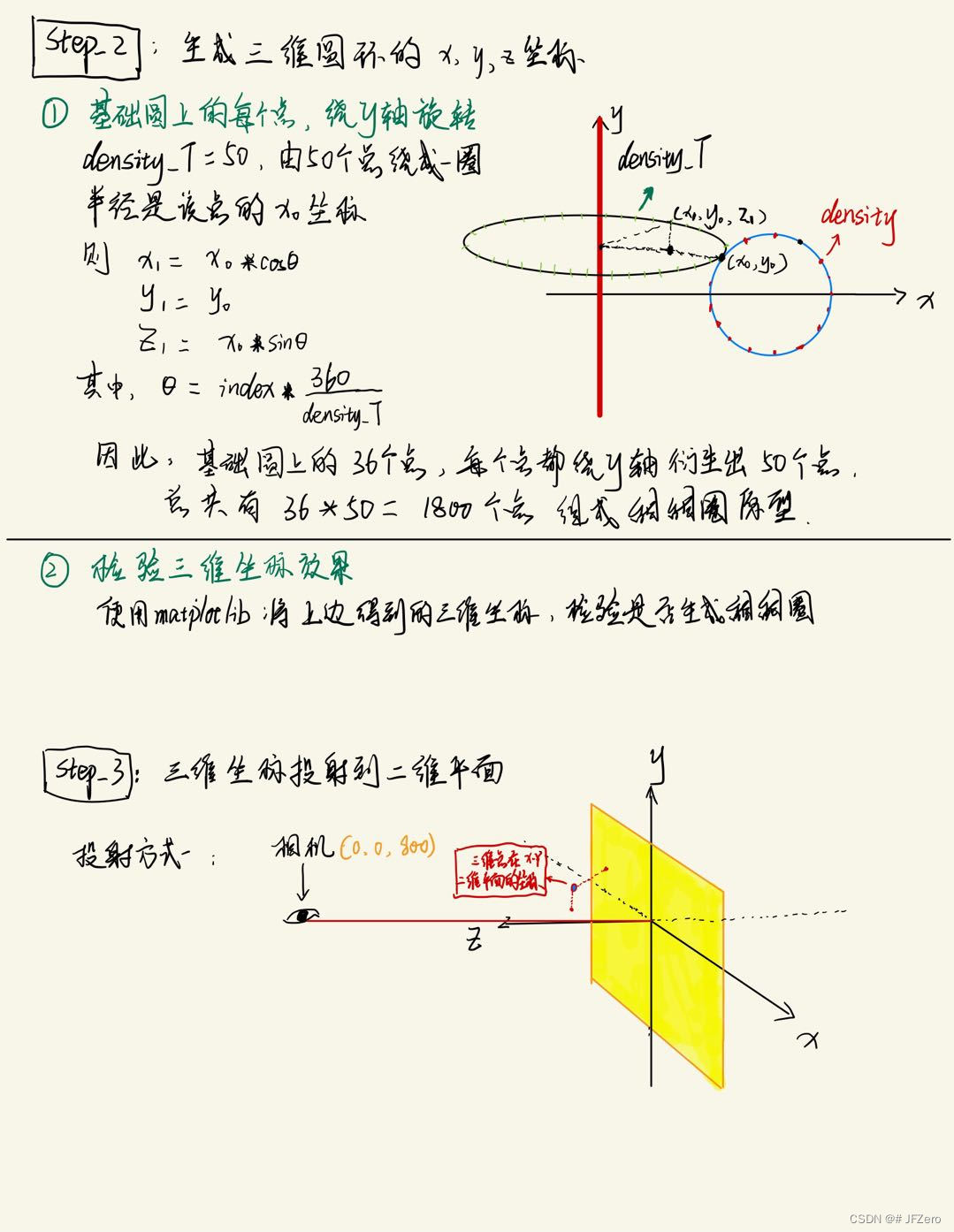
2. 演变为三维坐标，并检验三维坐标效果
3. 三维坐标投射到二维平面
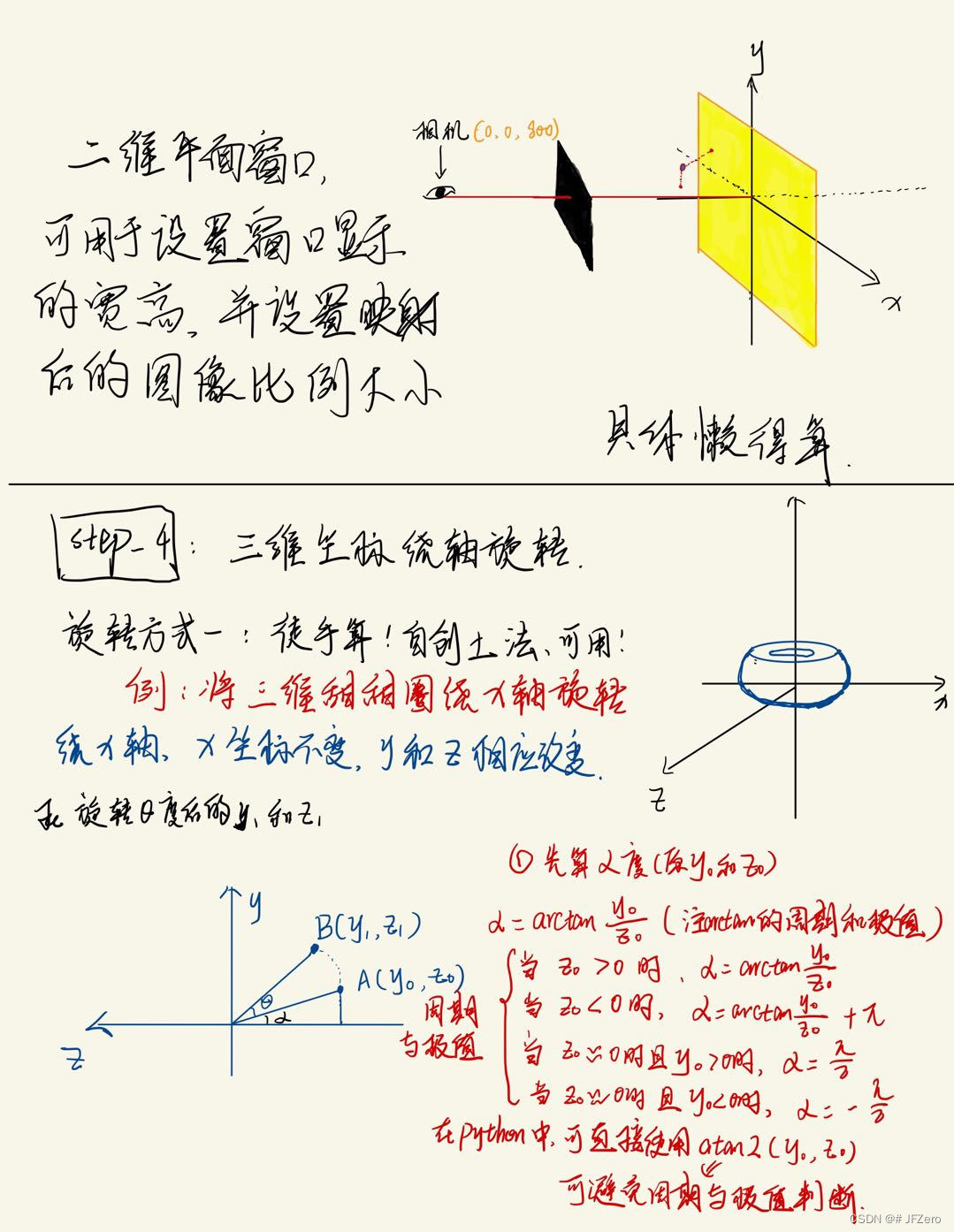
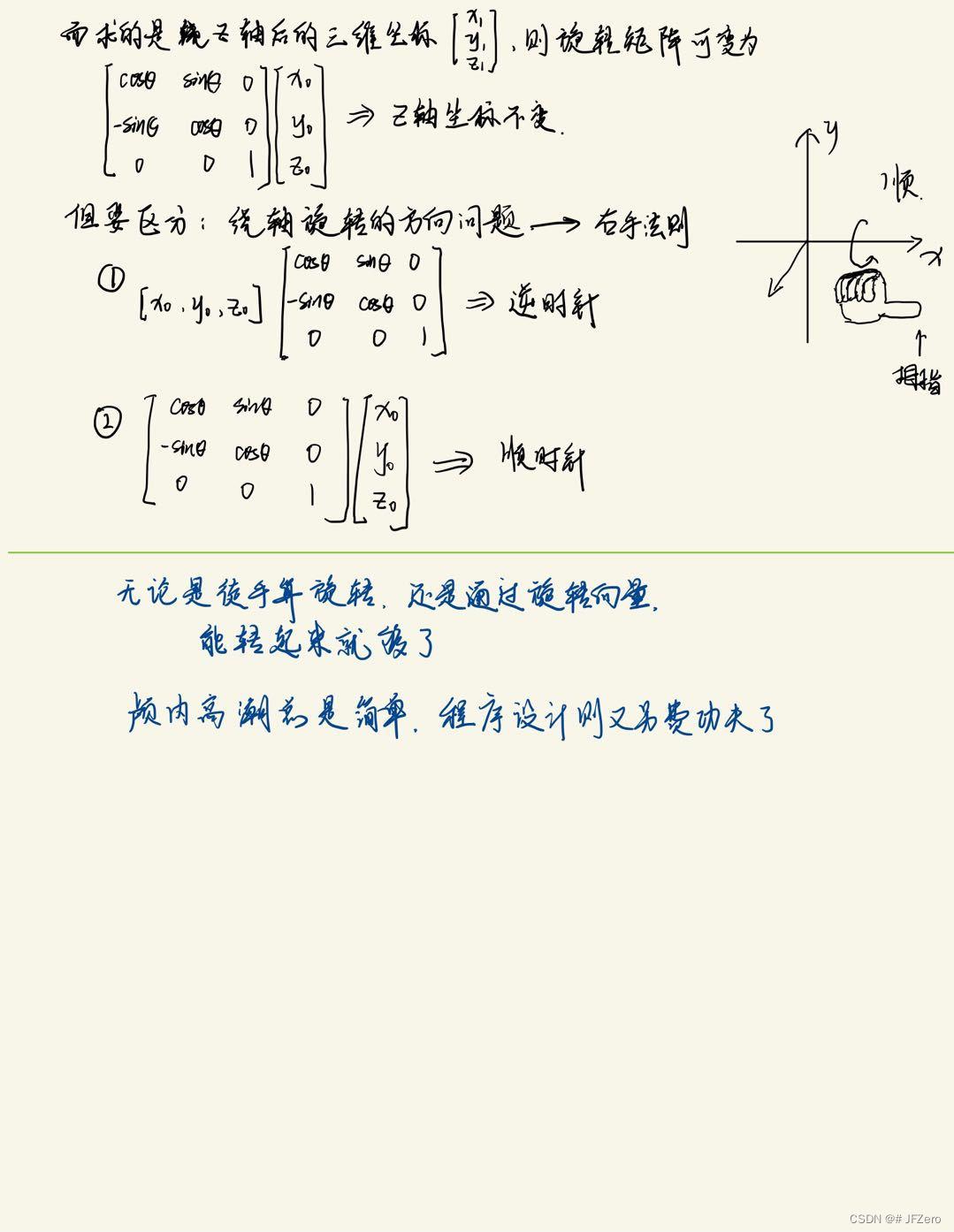
4. 三维坐标的旋转关系计算

全流程解析笔记

关键代码实现

• 形成基础圆

# turtle画图的基础框架
import turtle,math
turtle.tracer(0) # 取消绘画过程，一次性显示全部
pen = turtle.Pen()
pen.hideturtle()
pen.penup()

# 甜甜圈参数设置
density = 36 # 基础圆由36个点围城
circle_r = 50 # 基础圆
inside_r = 100 # 内环半径

# 生成二维圆坐标
for i in range(density):
    angle = i*math.pi*2/density
    circle_x = inside_r+circle_r+circle_r*math.cos(angle)
    circle_y = circle_r*math.sin(angle)

    # 绘制二维原坐标
    pen.goto(circle_x,circle_y)
    pen.dot(5)

turtle.update()
turtle.done()

• 二维基础圆推出三维坐标，并用matplotlib验证三维形状

for i in range(density):
    angle = i*math.pi*2/density
    circle_x = inside_r+circle_r+circle_r*math.cos(angle)
    circle_y = circle_r*math.sin(angle)

    # 获取该点绕y轴的三维坐标
    for T in range(density_T):
        angle_T = T * math.pi * 2 / density_T
        T_x = circle_x * math.cos(angle_T)
        T_z = circle_x * math.sin(angle_T)
        T_y = circle_y
        T_point_pos.append([T_x, T_y, T_z])

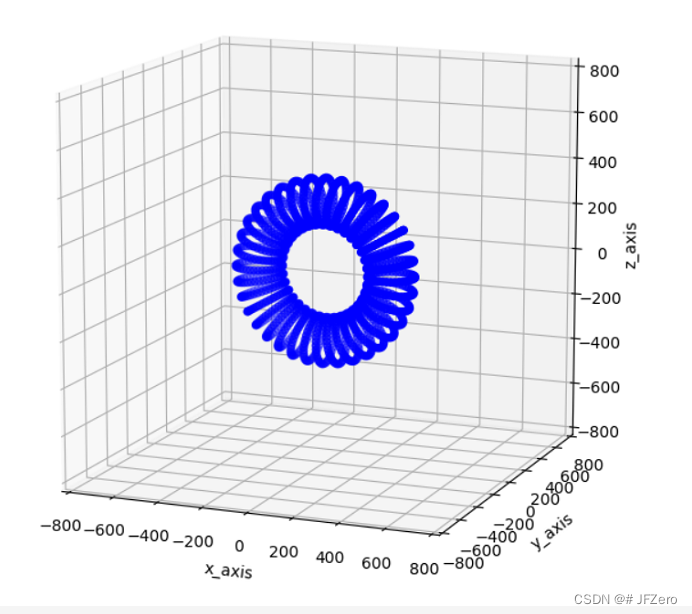
• 三维坐标映射到二维平面（最简单的相机+xy平面，没窗口）

    # 三维转二维——正视图
    for point in R_point_pos:
        x1 = camera_pos[2]*point[0]/(camera_pos[2]-point[2])
        y1 = camera_pos[2]*point[1]/(camera_pos[2]-point[2])
        z1 = point[2]
        pen.goto(x1,y1)
        dot_size = 5
        pen.dot(dot_size,"white")

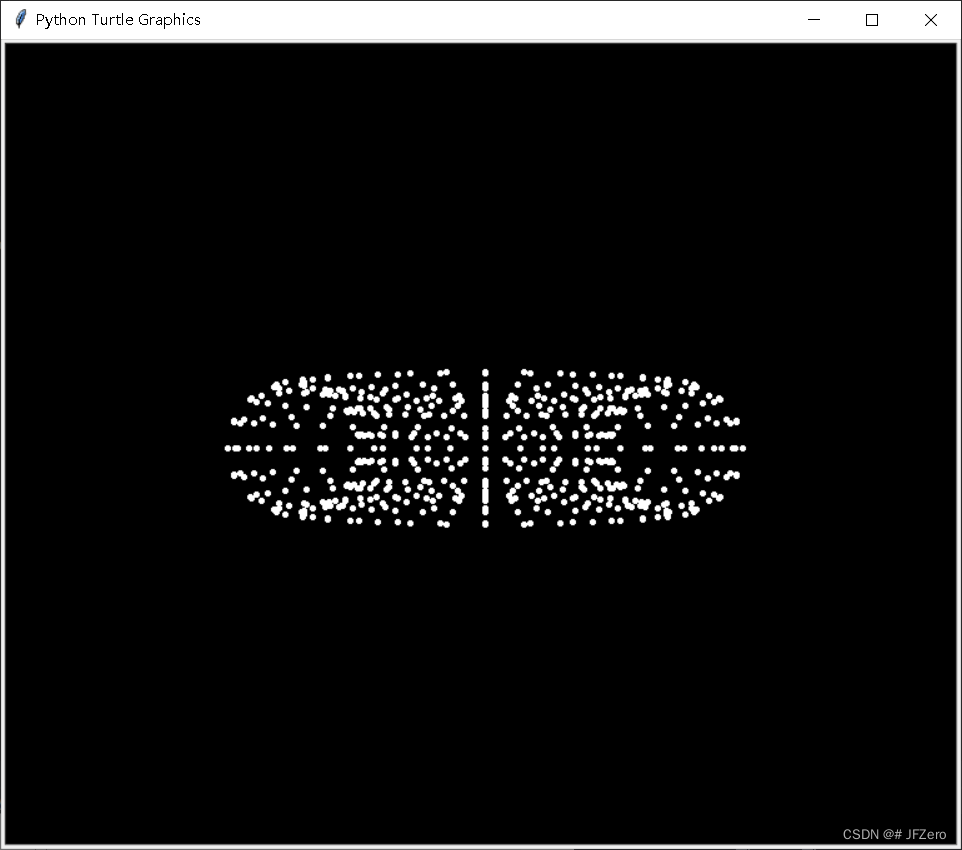
• 三维坐标绕轴旋转，然后再映射为二维
  徒手算角度，且没使用atan2()，直接用条件判断周期和极值

# 三维绕x轴旋转
angle_r = 2
while True:
    R_point_pos = []
    angle_r += 5
    for T in T_point_pos:
        try:
            if T[2]>0:
                beta = math.atan(T[1]/T[2])
            else:
                beta = math.atan(T[1]/T[2])+math.pi
        except:
            if T[1]>0:
                beta = math.pi/2
            else:
                beta = -math.pi/2
        r = math.sqrt(T[1]**2+T[2]**2)
        x = T[0]
        y = r*math.sin(beta-math.radians(angle_r))
        z = r*math.cos(beta-math.radians(angle_r))
        R_point_pos.append((x,y,z))
    # 三维转二维——正视图
    for point in R_point_pos:
        x1 = camera_pos[2]*point[0]/(camera_pos[2]-point[2])
        y1 = camera_pos[2]*point[1]/(camera_pos[2]-point[2])
        z1 = point[2]
        pen.goto(x1,y1)
        dot_size = 5
        pen.dot(dot_size,"white")
    turtle.update()
    # time.sleep(0.05)
    pen.clear()
    del R_point_pos
    turtle.clear()

完整的代码

import turtle
import math
turtle.tracer(0)
turtle.bgcolor("black")
pen = turtle.Pen()
pen.hideturtle()
pen.penup()

camera_pos = [0,0,800]
inside_r = 100
circle_r = 50
density = 15
density_T = 36
rotate_R = 36
T_point_pos = []

for i in range(density):
    angle = i*math.pi*2/density
    circle_x = inside_r+circle_r+circle_r*math.cos(angle)
    circle_y = circle_r*math.sin(angle)

    # 获取该点绕y轴的三维坐标
    for T in range(density_T):
        angle_T = T * math.pi * 2 / density_T
        T_x = circle_x * math.cos(angle_T)
        T_z = circle_x * math.sin(angle_T)
        T_y = circle_y
        T_point_pos.append([T_x, T_y, T_z])
# 三维绕x轴旋转
angle_r = 2
while True:
    R_point_pos = []
    angle_r += 5
    for T in T_point_pos:
        try:
            if T[2]>0:
                beta = math.atan(T[1]/T[2])
            else:
                beta = math.atan(T[1]/T[2])+math.pi
        except:
            if T[1]>0:
                beta = math.pi/2
            else:
                beta = -math.pi/2
        r = math.sqrt(T[1]**2+T[2]**2)
        x = T[0]
        y = r*math.sin(beta-math.radians(angle_r))
        z = r*math.cos(beta-math.radians(angle_r))
        R_point_pos.append((x,y,z))
    # 三维转二维——正视图
    for point in R_point_pos:
        x1 = camera_pos[2]*point[0]/(camera_pos[2]-point[2])
        y1 = camera_pos[2]*point[1]/(camera_pos[2]-point[2])
        z1 = point[2]
        pen.goto(x1,y1)
        dot_size = 5
        pen.dot(dot_size,"white")
    turtle.update()
    # time.sleep(0.05)
    pen.clear()
    del R_point_pos
    turtle.clear()

turtle.done()