1.神经网络的表示

对于这个两层的神经网络,输入层为
x
1
x1
x1,
x
2
x2
x2,
x
3
x3
x3可以用
a
[
0
]
a^{[0]}
a[0]代替,隐藏层记作
a
[
1
]
a^{[1]}
a[1],隐藏层包含有四个节点,所以是一个4x1的矩阵,如下所示
a
[
0
]
=
[
x
1
x
2
x
3
]
a^{[0]} = \begin{bmatrix} x1\\ x2\\ x3 \end{bmatrix}
a[0]=
x1x2x3
a
[
1
]
=
[
a
1
[
1
]
a
2
[
1
]
a
3
[
1
]
a
4
[
1
]
]
a^{[1]} = \begin{bmatrix} a_1^{[1]} \\ a_2^{[1]} \\ a_3^{[1]} \\ a_4^{[1]} \end{bmatrix}
a[1]=
a1[1]a2[1]a3[1]a4[1]

对于上述两层的神经网络的计算总共有两个步骤:
- 第一步,计算 z 1 [ 1 ] z_{1}^{[1]} z1[1], z 1 [ 1 ] z_{1}^{[1]} z1[1]= w 1 [ 1 ] T w_{1}^{[1]T} w1[1]T x {x} x+ b 1 [ 1 ] b_{1}^{[1]} b1[1]
- 第二步,通过激活函数计算
a
1
[
1
]
a_{1}^{[1]}
a1[1],
a
1
[
1
]
a_{1}^{[1]}
a1[1]=
σ
(
z
1
[
1
]
)
\sigma(z_{1}^{[1]})
σ(z1[1])
隐藏层的第二个以及后面的两个神经元计算过程一样,分别得到 a 2 [ 1 ] a_{2}^{[1]} a2[1], a 3 [ 1 ] a_{3}^{[1]} a3[1], a 4 [ 1 ] a_{4}^{[1]} a4[1],详细步骤如下:
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] ) z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] ) \begin{align*} z_1^{[1]} &= w_1^{[1]T}x + b_1^{[1]}, & a_1^{[1]} &= \sigma(z_1^{[1]}) \\ z_2^{[1]} &= w_2^{[1]T}x + b_2^{[1]}, & a_2^{[1]} &= \sigma(z_2^{[1]}) \\ z_3^{[1]} &= w_3^{[1]T}x + b_3^{[1]}, & a_3^{[1]} &= \sigma(z_3^{[1]}) \\ z_4^{[1]} &= w_4^{[1]T}x + b_4^{[1]}, & a_4^{[1]} &= \sigma(z_4^{[1]}) \end{align*} z1[1]z2[1]z3[1]z4[1]=w1[1]Tx+b1[1],=w2[1]Tx+b2[1],=w3[1]Tx+b3[1],=w4[1]Tx+b4[1],a1[1]a2[1]a3[1]a4[1]=σ(z1[1])=σ(z2[1])=σ(z3[1])=σ(z4[1])
单样本向量化,把上诉四个等式向量化。向量化的过程是将神经网络中的一层神经元参数纵向堆积起来,例如隐藏层中
w
w
w的纵向堆积起来变成一个的矩阵,用符号
W
[
1
]
W^{[1]}
W[1]表示。另一个看待这个的方法是我们有四个逻辑回归单元,且每一个逻辑回归单元都有相对应的参数——向量,把这四个向量堆积在一起,你会得出这4×3的矩阵。
公式1.1:
z
[
n
]
=
w
[
n
]
x
+
b
[
n
]
z^{[n]}=w^{[n]}x+b^{[n]}
z[n]=w[n]x+b[n]
公式1.2:
a
[
n
]
=
σ
(
z
[
n
]
)
a^{[n]}=\sigma(z^{[n]})
a[n]=σ(z[n])
详细过程如下:
公式1.3:
a
[
1
]
=
[
a
1
[
1
]
a
2
[
1
]
a
3
[
1
]
a
4
[
1
]
]
=
σ
(
z
[
1
]
)
a^{[1]} = \begin{bmatrix} a_1^{[1]} \\ a_2^{[1]} \\ a_3^{[1]} \\ a_4^{[1]} \end{bmatrix} = \sigma(z^{[1]})
a[1]=
a1[1]a2[1]a3[1]a4[1]
=σ(z[1])
公式1.4:
[
z
1
[
1
]
z
2
[
1
]
z
3
[
1
]
z
4
[
1
]
]
=
[
⋯
W
1
[
1
]
T
⋯
⋯
W
2
[
1
]
T
⋯
⋯
W
3
[
1
]
T
⋯
⋯
W
4
[
1
]
T
⋯
]
⋅
[
x
1
x
2
x
3
]
+
[
b
1
[
1
]
b
2
[
1
]
b
3
[
1
]
b
4
[
1
]
]
\begin{bmatrix} z_1^{[1]} \\ z_2^{[1]} \\ z_3^{[1]} \\ z_4^{[1]} \end{bmatrix} = \begin{bmatrix} \cdots & W_1^{[1]T} & \cdots \\ \cdots & W_2^{[1]T} & \cdots \\ \cdots & W_3^{[1]T} & \cdots \\ \cdots & W_4^{[1]T} & \cdots \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} b_1^{[1]} \\ b_2^{[1]} \\ b_3^{[1]} \\ b_4^{[1]} \end{bmatrix}
z1[1]z2[1]z3[1]z4[1]
=
⋯⋯⋯⋯W1[1]TW2[1]TW3[1]TW4[1]T⋯⋯⋯⋯
⋅
x1x2x3
+
b1[1]b2[1]b3[1]b4[1]
对于神经网络的第一层,给予一个输入x,得到
a
[
1
]
a^{[1]}
a[1],x可以表示为
a
[
0
]
a^{[0]}
a[0]。通过相似的衍生你会发现,后一层的表示同样可以写成类似的形式,得到
a
[
2
]
a^{[2]}
a[2],
y
^
=
a
[
2
]
\hat y=a^{[2]}
y^=a[2],具体过程见公式1.1、1.2。

2.多样本向量化
上一节讲述了深度神经网络的基础。它们公用的如向量 a [ 1 ] a^{[1]} a[1]、 a [ 2 ] a^{[2]} a[2]、 z [ 1 ] z^{[1]} z[1]、 z [ 2 ] z^{[2]} z[2]。
对于一个给定的输入向量 X X X,这四个等式可以计算出 a [ 2 ] a^{[2]} a[2]等于 y ^ \hat y y^。这是针对于每一层的激活状态。如果有m个训练样本,那么这些变量是这个过程。
用第一个训练样本来计算 y ^ [ 1 ] \hat y^{[1]} y^[1],就是第一个训练样本上导出的结果。
然后,用 x [ 2 ] x^{[2]} x[2]来计算出预测值 y ^ [ 2 ] \hat y^{[2]} y^[2],循环往复直到用 x [ m ] 计算出 x^{[m]}计算出 x[m]计算出 y ^ [ m ] \hat y^{[m]} y^[m]
用激活函数表示法,如下图左下表示写为 a [ 2 ] ( 1 ) a^{[2](1)} a[2](1)和 a [ 2 ] ( m ) a^{[2](m)} a[2](m)。

【注意】:
a
[
2
]
(
i
)
,
(
i
)
a^{[2](i)},(i)
a[2](i),(i)是指第
i
i
i个训练样本而
[
2
]
[2]
[2]是指第二层。
如果有一个非向量化形式的实现,而且要计算出它的预测值,对于所有训练样本,需要让
i
i
i从1到实现这四个等式:
z
[
1
]
(
i
)
=
W
[
1
]
(
i
)
a
[
i
]
+
b
[
1
]
(
i
)
z^{[1](i)} = W^{[1](i)} a^{[i]} + b^{[1](i)}
z[1](i)=W[1](i)a[i]+b[1](i)
a
[
1
]
(
i
)
=
σ
(
z
[
1
]
(
i
)
)
a^{[1](i)} = \sigma(z^{[1](i)})
a[1](i)=σ(z[1](i))
z
[
2
]
(
i
)
=
W
[
2
]
(
i
)
a
[
1
]
(
i
)
+
b
[
2
]
(
i
)
z^{[2](i)} = W^{[2](i)} a^{[1](i)} + b^{[2](i)}
z[2](i)=W[2](i)a[1](i)+b[2](i)
a
[
2
]
(
i
)
=
σ
(
z
[
2
]
(
i
)
)
a^{[2](i)} = \sigma(z^{[2](i)})
a[2](i)=σ(z[2](i))
对于上面的这个方程中的
i
i
i,是所有依赖于训练样本的变量,即将
i
i
i添加到
x
x
x,
z
z
z和
a
a
a。如果想计算个训练样本上的所有输出,就应该向量化整个计算,以简化这列。
x
=
[
⋮
⋮
⋮
⋮
x
(
1
)
x
(
1
)
⋯
x
(
m
)
⋮
⋮
⋮
⋮
]
x=\begin{bmatrix} \vdots & \vdots & \vdots& \vdots & \\ x^{(1)} & x^{(1)} &\cdots&x^{(m)} & \\ \vdots &\vdots & \vdots & \vdots & \end{bmatrix}
x=
⋮x(1)⋮⋮x(1)⋮⋮⋯⋮⋮x(m)⋮
Z
[
1
]
=
[
⋮
⋮
⋮
⋮
z
[
1
]
(
1
)
z
[
1
]
(
2
)
⋯
z
[
1
]
(
m
)
⋮
⋮
⋮
⋮
]
Z^{[1]}=\begin{bmatrix} \vdots & \vdots & \vdots& \vdots & \\ z^{[1](1)} & z^{[1](2)}&\cdots&z^{[1](m)}& \\ \vdots &\vdots & \vdots & \vdots & \end{bmatrix}
Z[1]=
⋮z[1](1)⋮⋮z[1](2)⋮⋮⋯⋮⋮z[1](m)⋮
A
[
1
]
=
[
⋮
⋮
⋮
⋮
a
[
1
]
(
1
)
a
[
1
]
(
2
)
⋯
a
[
1
]
(
m
)
⋮
⋮
⋮
⋮
]
A^{[1]}=\begin{bmatrix} \vdots & \vdots & \vdots& \vdots & \\ a^{[1](1)} &a^{[1](2)}&\cdots&a^{[1](m)}& \\ \vdots &\vdots & \vdots & \vdots & \end{bmatrix}
A[1]=
⋮a[1](1)⋮⋮a[1](2)⋮⋮⋯⋮⋮a[1](m)⋮
z
[
1
]
(
i
)
=
W
[
1
]
(
i
)
a
(
i
)
+
b
[
1
]
a
[
1
]
(
i
)
=
σ
(
z
[
1
]
(
i
)
)
z
[
2
]
(
i
)
=
W
[
2
]
(
i
)
a
[
1
]
(
i
)
+
b
[
2
]
a
[
2
]
(
i
)
=
σ
(
z
[
2
]
(
i
)
)
⇒
{
A
[
1
]
=
σ
(
Z
[
1
]
)
Z
[
2
]
=
W
[
2
]
A
[
1
]
+
b
[
2
]
A
[
2
]
=
σ
(
Z
[
2
]
)
\begin{align*} z^{[1](i)} &= W^{[1](i)} a^{(i)} + b^{[1]} \\ a^{[1](i)} &= \sigma(z^{[1](i)}) \\ z^{[2](i)} &= W^{[2](i)} a^{[1](i)} + b^{[2]} \\ a^{[2](i)} &= \sigma(z^{[2](i)}) \end{align*} \Rightarrow \begin{cases} A^{[1]} = \sigma(Z^{[1]}) \\ Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]} \\ A^{[2]} = \sigma(Z^{[2]}) \end{cases}
z[1](i)a[1](i)z[2](i)a[2](i)=W[1](i)a(i)+b[1]=σ(z[1](i))=W[2](i)a[1](i)+b[2]=σ(z[2](i))⇒⎩
⎨
⎧A[1]=σ(Z[1])Z[2]=W[2]A[1]+b[2]A[2]=σ(Z[2])
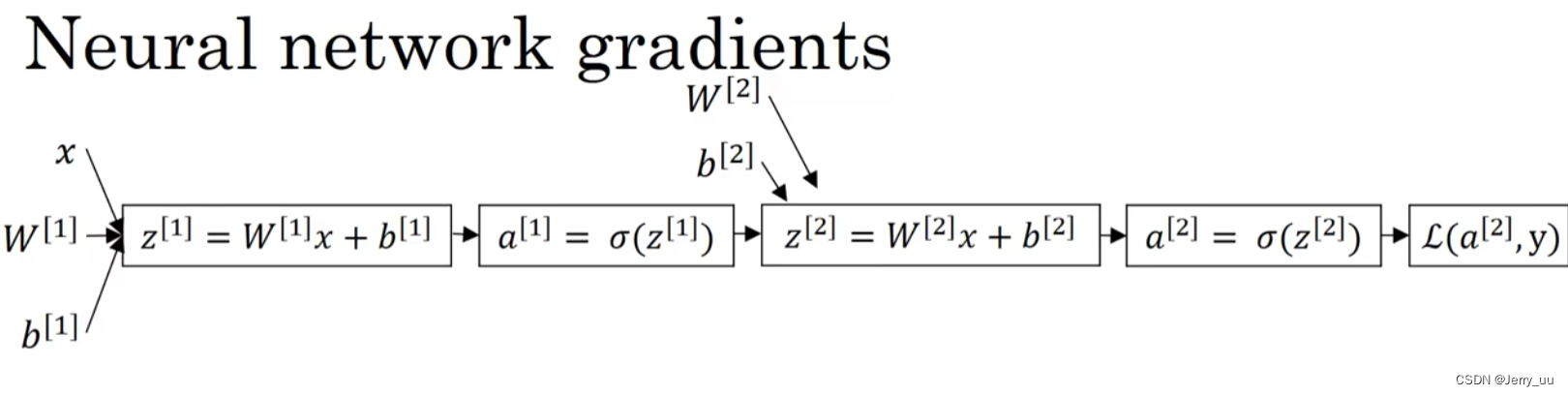
-
输入向量: x x x
-
第一层的权重和偏置: W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1]
-
第一层的线性变换: z [ 1 ] = W [ 1 ] x + b [ 1 ] z^{[1]} = W^{[1]}x + b^{[1]} z[1]=W[1]x+b[1]
-
第一层使用sigmoid函数的激活: a [ 1 ] = σ ( z [ 1 ] ) a^{[1]} = \sigma(z^{[1]}) a[1]=σ(z[1]),其中 σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
-
第二层的权重和偏置: W [ 2 ] W^{[2]} W[2], b [ 2 ] b^{[2]} b[2]
-
第二层的线性变换: z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} z[2]=W[2]a[1]+b[2]
-
第二层使用sigmoid函数的激活: a [ 2 ] = σ ( z [ 2 ] ) a^{[2]} = \sigma(z^{[2]}) a[2]=σ(z[2])
-
损失函数: L ( a [ 2 ] , y ) \mathcal{L}(a^{[2]}, y) L(a[2],y),对于二分类问题,交叉熵损失函数定义为 − ( y log ( a [ 2 ] ) + ( 1 − y ) log ( 1 − a [ 2 ] ) ) -\left( y\log(a^{[2]}) + (1-y)\log(1-a^{[2]}) \right) −(ylog(a[2])+(1−y)log(1−a[2])),其中 y y y 是真实标签(0或1), a [ 2 ] a^{[2]} a[2] 是预测概率,表示为正类的概率。
3.核对矩阵维度

举个例子:
z
[
1
]
=
W
[
1
]
⋅
x
+
b
[
1
]
z^{[1]} = W^{[1]} \cdot x + b^{[1]}
z[1]=W[1]⋅x+b[1]
从上图可以看出:
x
x
x 的维度是 (2,1),且
z
[
1
]
z^{[1]}
z[1] 的维度是 (3,1)。由于等式两边维度一致,因此可以推出
W
[
1
]
W^{[1]}
W[1] 的维度为 (3,2),且
b
[
1
]
b^{[1]}
b[1] 也为 (3,1)。从正面看,因为第 1 层有 3 个神经元,且有 2 个输入,因此每个神经元中的参数要分别与两个输入相乘,也很容易得出
W
[
1
]
W^{[1]}
W[1] 的维度。同理可以推出后面层的参数的维度,总结规律是:
W
[
l
]
=
(
n
[
l
]
,
n
[
l
−
1
]
)
W^{[l]} = (n^{[l]}, n^{[l-1]})
W[l]=(n[l],n[l−1])
a
[
l
]
=
(
n
[
l
]
,
1
)
a^{[l]} = (n^{[l]}, 1)
a[l]=(n[l],1)
z
[
l
]
=
b
[
l
]
=
(
n
[
l
]
,
1
)
z^{[l]} = b^{[l]} = (n^{[l]}, 1)
z[l]=b[l]=(n[l],1)
d
x
dx
dx 和
x
x
x 的维度相同若有
m
m
m个样本,将公式向量化之后只需将
a
[
l
]
a^{[l]}
a[l] 和
z
[
l
]
z^{[l]}
z[l] 改为大写,并将 1 改为
m
m
m 即可(对
b
b
b,Python 的广播机制将其维数从 1 变为
m
m
m)。
4.前向传播
| 参数 | 类型 | 描述 |
|---|---|---|
| x ( i ) x^{(i)} x(i) | x ( i ) \mathbf{x}^{(i)} x(i) | 输入样本 i i i |
| W [ 1 ] W^{[1]} W[1] | W [ 1 ] \mathbf{W}^{[1]} W[1] | 第一层权重矩阵 |
| b [ 1 ] ( i ) b^{[1] (i)} b[1](i) | b [ 1 ] \mathbf{b}^{[1]} b[1] | 第一层偏置向量 |
| z [ 1 ] ( i ) z^{[1] (i)} z[1](i) | z 1 ( i ) z^{(i)}_1 z1(i) | 第一层输出 |
| a [ 1 ] ( i ) a^{[1] (i)} a[1](i) | a 1 ( i ) a^{(i)}_1 a1(i) | 第一层激活值 |
| W [ 2 ] W^{[2]} W[2] | W [ 2 ] \mathbf{W}^{[2]} W[2] | 第二层权重矩阵 |
| b [ 2 ] ( i ) b^{[2] (i)} b[2](i) | b [ 2 ] \mathbf{b}^{[2]} b[2] | 第二层偏置向量 |
| z [ 2 ] ( i ) z^{[2] (i)} z[2](i) | z 2 ( i ) z^{(i)}_2 z2(i) | 第二层输出 |
| y ^ ( i ) \hat{y}^{(i)} y^(i) | y ^ ( i ) \hat{y}^{(i)} y^(i) | 神经网络的预测值 |
| y ( i ) y^{(i)} y(i) | y ( i ) y^{(i)} y(i) | 真实标签 |
| y prediction ( i ) y^{(i)}_{\text{prediction}} yprediction(i) | y prediction ( i ) y^{(i)}_{\text{prediction}} yprediction(i) | 预测是否正确 |
| m m m | m m m | 样本数量 |
| J J J | J J J | 损失函数 |
对于一个样本 x ( i ) x^{(i)} x(i):
z [ 1 ] ( i ) = W [ 1 ] x ( i ) + b [ 1 ] ( i ) (1) z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)} \tag{1} z[1](i)=W[1]x(i)+b[1](i)(1)
a [ 1 ] ( i ) = tanh ( z [ 1 ] ( i ) ) (2) a^{[1] (i)} = \tanh(z^{[1] (i)}) \tag{2} a[1](i)=tanh(z[1](i))(2)
z [ 2 ] ( i ) = W [ 2 ] a [ 1 ] ( i ) + b [ 2 ] ( i ) (3) z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)} \tag{3} z[2](i)=W[2]a[1](i)+b[2](i)(3)
y ^ ( i ) = a [ 2 ] ( i ) = σ ( z [ 2 ] ( i ) ) (4) \hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{[2] (i)}) \tag{4} y^(i)=a[2](i)=σ(z[2](i))(4)
y prediction ( i ) = { 1 if a [ 2 ] ( i ) > 0.5 0 otherwise (5) y^{(i)}_{\text{prediction}} = \begin{cases} 1 & \text{if } a^{[2](i)} > 0.5 \\ 0 & \text{otherwise} \end{cases} \tag{5} yprediction(i)={10if a[2](i)>0.5otherwise(5)
给定所有样本的预测值,你也可以计算代价 J J J 如下:
J = − 1 m ∑ i = 0 m ( y ( i ) log ( a [ 2 ] ( i ) ) + ( 1 − y ( i ) ) log ( 1 − a [ 2 ] ( i ) ) ) (6) J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \left( y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \right) \tag{6} J=−m1i=0∑m(y(i)log(a[2](i))+(1−y(i))log(1−a[2](i)))(6)
5.反向传播

-
对于第二层的 z z z 值的偏导数:
∂ J ∂ z 2 ( i ) = 1 m ( a [ 2 ] ( i ) − y ( i ) ) \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } = \frac{1}{m} (a^{[2](i)} - y^{(i)}) ∂z2(i)∂J=m1(a[2](i)−y(i)) -
对于第二层权重 W 2 W_2 W2 的偏导数:
∂ J ∂ W 2 = ∂ J ∂ z 2 ( i ) a [ 1 ] ( i ) T \frac{\partial \mathcal{J} }{ \partial W_2 } = \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } a^{[1] (i) T} ∂W2∂J=∂z2(i)∂Ja[1](i)T -
对于第二层偏置 b 2 b_2 b2 的偏导数:
∂ J ∂ b 2 = ∑ i ∂ J ∂ z 2 ( i ) \frac{\partial \mathcal{J} }{ \partial b_2 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)}}} ∂b2∂J=∑i∂z2(i)∂J -
对于第一层的 z z z 值的偏导数:
∂ J ∂ z 1 ( i ) = W 2 T ∂ J ∂ z 2 ( i ) ∗ ( 1 − a [ 1 ] ( i ) 2 ) \frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } = W_2^T \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } * ( 1 - a^{[1] (i) 2}) ∂z1(i)∂J=W2T∂z2(i)∂J∗(1−a[1](i)2) -
对于第一层权重 W 1 W_1 W1 的偏导数:
∂ J ∂ W 1 = ∂ J ∂ z 1 ( i ) X T \frac{\partial \mathcal{J} }{ \partial W_1 } = \frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } X^T ∂W1∂J=∂z1(i)∂JXT -
对于第一层偏置 b 1 b_1 b1 的偏导数:
∂ J i ∂ b 1 = ∑ i ∂ J ∂ z 1 ( i ) \frac{\partial \mathcal{J} _i }{ \partial b_1 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)}}} ∂b1∂Ji=∑i∂z1(i)∂J
请注意,星号 ( * ) 表示元素级乘法。

以上图为例, 我们先计算
L
=
−
y
log
(
a
[
2
]
)
−
(
1
−
y
)
log
(
1
−
a
[
2
]
)
L = -y\log(a^{[2]}) - (1 - y)\log(1 - a^{[2]})
L=−ylog(a[2])−(1−y)log(1−a[2])。
d a [ 2 ] da^{[2]} da[2] 对应于 a [ 2 ] a^{[2]} a[2] 的梯度, 根据 d a [ 2 ] = d L d a [ 2 ] = − y a [ 2 ] + 1 − y 1 − a [ 2 ] da^{[2]} =\frac {dL}{da^{[2]}}= \frac{-y}{a^{[2]}} + \frac{1-y}{1-a^{[2]}} da[2]=da[2]dL=a[2]−y+1−a[2]1−y。
根据链式法则计算 d z [ 2 ] = d a [ 2 ] ∗ d a [ 2 ] d z [ 2 ] dz^{[2]} = da^{[2]} *\frac{da^{[2]}}{dz^{[2]}} dz[2]=da[2]∗dz[2]da[2]。
因为 a [ 2 ] = sigmoid ( z [ 2 ] ) a^{[2]} = \text{sigmoid}(z^{[2]}) a[2]=sigmoid(z[2]),所以 d a [ 2 ] d z [ 2 ] = a [ 2 ] ( 1 − a [ 2 ] ) \frac{da^{[2]}}{dz^{[2]}} = a^{[2]}(1 - a^{[2]}) dz[2]da[2]=a[2](1−a[2])。
因此 d z [ 2 ] = − y a [ 2 ] ( 1 − a [ 2 ] ) + 1 − y 1 − a [ 2 ] a [ 2 ] = a [ 2 ] − y dz^{[2]} = \frac{-y}{a^{[2]}} (1 - a^{[2]}) + \frac{1-y}{1-a^{[2]}} a^{[2]} = a^{[2]} - y dz[2]=a[2]−y(1−a[2])+1−a[2]1−ya[2]=a[2]−y。
d w [ 2 ] = d z [ 2 ] ∗ d z [ 2 ] d w [ 2 ] dw^{[2]} = dz^{[2]} *\frac{dz^{[2]}}{dw^{[2]}} dw[2]=dz[2]∗dw[2]dz[2], z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]} = w^{[2]}a^{[1]} + b^{[2]} z[2]=w[2]a[1]+b[2],
根据链式法则计算
a
[
1
]
=
d
z
[
2
]
d
w
[
2
]
a^{[1]} = \frac{dz^{[2]}}{dw^{[2]}}
a[1]=dw[2]dz[2],
a
[
1
]
a^{[1]}
a[1] 是关于
w
[
2
]
w^{[2]}
w[2] 的函数,
d
z
[
2
]
dz^{[2]}
dz[2] 的链式法则计算
d
w
[
2
]
dw^{[2]}
dw[2]。
(
n
[
2
]
,
1
)
(n^{[2]}, 1)
(n[2],1),
d
w
[
2
]
dw^{[2]}
dw[2] 的维度为
(
n
[
2
]
,
n
[
1
]
)
(n^{[2]}, n^{[1]})
(n[2],n[1]),
a
[
1
]
a^{[1]}
a[1] 的维度和
w
[
2
]
w^{[2]}
w[2] 的维度相同。
(
n
[
1
]
,
1
)
(n^{[1]}, 1)
(n[1],1),因此,
d
z
[
2
]
dz^{[2]}
dz[2] 是
w
[
2
]
w^{[2]}
w[2] 的函数,所以
d
z
[
2
]
dz^{[2]}
dz[2] 可以表示为,用
a
[
1
]
a^{[1]}
a[1] 的函数表示。
所以 d w [ 2 ] = d z [ 2 ] × a [ 1 ] T dw^{[2]} = dz^{[2]} \times a^{[1]T} dw[2]=dz[2]×a[1]T, d b [ 2 ] = d z [ 2 ] × d z [ 2 ] d b [ 2 ] = d z [ 2 ] db^{[2]} = dz^{[2]} \times \frac{dz^{[2]}}{db^{[2]}} = dz^{[2]} db[2]=dz[2]×db[2]dz[2]=dz[2]。
接下来计算 d a [ 1 ] da^{[1]} da[1],
d a [ 1 ] = d z [ 2 ] ∗ d z [ 2 ] d a [ 1 ] da^{[1]} = dz^{[2]}* \frac{dz^{[2]}}{da^{[1]}} da[1]=dz[2]∗da[1]dz[2], z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]} = w^{[2]}a^{[1]} + b^{[2]} z[2]=w[2]a[1]+b[2], d z [ 2 ] d a [ 1 ] = w [ 2 ] \frac{dz^{[2]}}{da^{[1]}} = w^{[2]} da[1]dz[2]=w[2]。
因此 d a [ 1 ] = w [ 2 ] T d z [ 2 ] da^{[1]} = w^{[2]T} dz^{[2]} da[1]=w[2]Tdz[2], d a [ 1 ] da^{[1]} da[1] 的维度和 a [ 1 ] a^{[1]} a[1] 的维度相同,即 ( n [ 1 ] , 1 ) (n^{[1]}, 1) (n[1],1), w [ 2 ] w^{[2]} w[2] 的维度为 ( n [ 2 ] , n [ 1 ] ) (n^{[2]}, n^{[1]}) (n[2],n[1]), d z [ 2 ] dz^{[2]} dz[2] 的维度为 ( n [ 2 ] , 1 ) (n^{[2]}, 1) (n[2],1),所以关于 w [ 2 ] w^{[2]} w[2] 的函数为 d z [ 2 ] dz^{[2]} dz[2] 的函数。
d z [ 1 ] = d a [ 1 ] ∗ d a [ 1 ] d z [ 1 ] = w [ 2 ] T d z [ 2 ] ∗ ( sigmoid函数的导数 ) = w [ 2 ] T d z [ 2 ] ∗ ( 1 − a [ 1 ] 2 ) dz^{[1]} = da^{[1]} \ast \frac{da^{[1]}}{dz^{[1]}} = w^{[2]T} dz^{[2]} \ast (\text{sigmoid函数的导数})=w^{[2]T} dz^{[2]}*(1-a^{[1]2}) dz[1]=da[1]∗dz[1]da[1]=w[2]Tdz[2]∗(sigmoid函数的导数)=w[2]Tdz[2]∗(1−a[1]2)。
d w [ 1 ] = d z [ 1 ] × x [ 1 ] T dw^{[1]} = dz^{[1]} \times x^{[1]T} dw[1]=dz[1]×x[1]T, d z [ 1 ] = d z [ 1 ] d w [ 1 ] dz^{[1]} = \frac{dz^{[1]}}{dw^{[1]}} dz[1]=dw[1]dz[1]。
d b [ 1 ] = d z [ 1 ] db^{[1]} = dz^{[1]} db[1]=dz[1]。
sigmoid函数求导
f ′ ( x ) = d d x [ 1 1 + e − x ] = ( 1 + e − x ) ⋅ d d x [ 1 + e − x ] − 1 ⋅ d d x [ e − x ] ( 1 + e − x ) 2 = ( 1 + e − x ) ⋅ ( − e − x ) − 1 ⋅ ( − e − x ) ( 1 + e − x ) 2 = e − x ( 1 + e − x ) 2 \begin{aligned} f'(x) &= \frac{d}{dx} \left[ \frac{1}{1 + e^{-x}} \right] \ &= \frac{(1 + e^{-x}) \cdot \frac{d}{dx} [1 + e^{-x}] - 1 \cdot \frac{d}{dx} [e^{-x}]}{(1 + e^{-x})^2} \ &= \frac{(1 + e^{-x}) \cdot (-e^{-x}) - 1 \cdot (-e^{-x})}{(1 + e^{-x})^2} \ &= \frac{e^{-x}}{(1 + e^{-x})^2} \end{aligned} f′(x)=dxd[1+e−x1] =(1+e−x)2(1+e−x)⋅dxd[1+e−x]−1⋅dxd[e−x] =(1+e−x)2(1+e−x)⋅(−e−x)−1⋅(−e−x) =(1+e−x)2e−x
6.作业部分(举个例子,其他分开写)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
这段py代码是sigmoid函数的梯度
其中激活函数的输出为
A
L
=
1
1
+
e
−
Z
AL=\frac{1}{1 + e^{-Z}}
AL=1+e−Z1,Z表示线性层的输出。
-
对于 sigmoid 激活函数,损失函数为交叉熵损失函数:
L = − ( Y ⋅ log ( A L ) + ( 1 − Y ) ⋅ log ( 1 − A L ) ) L = - (Y \cdot \log(AL) + (1 - Y) \cdot \log(1 - AL)) L=−(Y⋅log(AL)+(1−Y)⋅log(1−AL)) -
其中,Y 是真实标签,AL 是神经网络的输出。根据链式法则,我们可以将交叉熵损失函数对 AL 的梯度表示为:
d L d A L = − ( Y A L − 1 − Y 1 − A L ) \frac{dL}{dAL} = - \left( \frac{Y}{AL} - \frac{1 - Y}{1 - AL} \right)\ dALdL=−(ALY−1−AL1−Y)-
首先,将 np.divide(Y, AL) 和 np.divide(1 - Y, 1 - AL) 分别求导:
d d A L [ Y A L ] = 1 A L − Y A L 2 \frac{d}{dAL} \left[ \frac{Y}{AL} \right] = \frac{1}{AL} - \frac{Y}{AL^2} dALd[ALY]=AL1−AL2Y
d d A L [ 1 − Y 1 − A L ] = − 1 1 − A L − 1 − Y ( 1 − A L ) 2 \frac{d}{dAL} \left[ \frac{1 - Y}{1 - AL} \right] = \frac{-1}{1 - AL} - \frac{1 - Y}{(1 - AL)^2} dALd[1−AL1−Y]=1−AL−1−(1−AL)21−Y -
然后,将这两个导数相加:
-
d d A L [ − Y A L + 1 − Y 1 − A L ] = − d d A L [ Y A L ] + d d A L [ 1 − Y 1 − A L ] = − ( 1 A L − Y A L 2 ) + ( − 1 1 − A L − 1 − Y ( 1 − A L ) 2 ) = − 1 A L + 1 1 − A L + Y A L 2 + Y ( 1 − A L ) 2 = − 1 A L + 1 1 − A L + Y A L ( 1 − A L ) \begin{aligned} \frac{d}{dAL} \left[ - \frac{Y}{AL} + \frac{1 - Y}{1 - AL} \right] &= - \frac{d}{dAL} \left[ \frac{Y}{AL} \right] + \frac{d}{dAL} \left[ \frac{1 - Y}{1 - AL} \right] \ &= - \left( \frac{1}{AL} - \frac{Y}{AL^2} \right) + \left( \frac{-1}{1 - AL} - \frac{1 - Y}{(1 - AL)^2} \right) \ &= - \frac{1}{AL} + \frac{1}{1 - AL} + \frac{Y}{AL^2} + \frac{Y}{(1 - AL)^2} \ &= \frac{-1}{AL} + \frac{1}{1 - AL} + \frac{Y}{AL(1 - AL)} \end{aligned} dALd[−ALY+1−AL1−Y]=−dALd[ALY]+dALd[1−AL1−Y] =−(AL1−AL2Y)+(1−AL−1−(1−AL)21−Y) =−AL1+1−AL1+AL2Y+(1−AL)2Y =AL−1+1−AL1+AL(1−AL)Y
- 最后,整理一下表达式:
d L d A L = − 1 A L + 1 1 − A L − Y A L + Y 1 − A L = − Y A L + 1 − Y 1 − A L \frac{dL}{dAL} = \frac{-1}{AL} + \frac{1}{1 - AL} - \frac{Y}{AL} + \frac{Y}{1 - AL} = - \frac{Y}{AL} + \frac{1 - Y}{1 - AL} dALdL=AL−1+1−AL1−ALY+1−ALY=−ALY+1−AL1−Y
【参考】:
1.https://www.cnblogs.com/southtonorth/p/9512559.html
2.https://zhuanlan.zhihu.com/p/161458241
3.http://www.ai-start.com/dl2017/html/lesson1-week3.html






















 1325
1325











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








