L1 神经网络和深度学习 Week3（吴恩达）

1. 单层的Logistic回归

引用吴恩达老师课上的图（3.10）

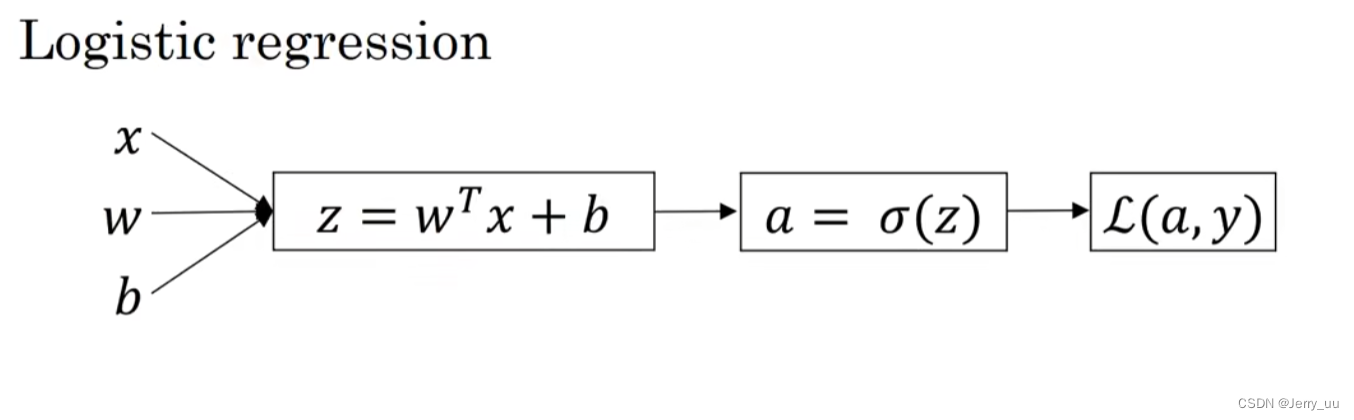
算法的数学表达式：

对于一个样本 $x^{(i)}$：
$$z^{(i)}=w^T{x}^{(i)}+b\text{\hspace{1em}(1)}$$
$${\hat{y}}^{(i)}=a^{(i)}=sigmoid(z^{(i)})\text{\hspace{1em}(2)}$$
$$\mathcal{L}(a^{(i)},y^{(i)})=-y^{(i)}\log (a^{(i)})-(1-y^{(i)})\log (1-a^{(i)})\text{\hspace{1em}(3)}$$

然后通过对所有训练样本求和来计算成本：
$$J=\frac{1}{m}\sum _{i=1}^m\mathcal{L}(a^{(i)},y^{(i)})\text{\hspace{1em}(6)}$$

以下都为多个样本，上述为单个样本的算法表达式

• 正向传播
  • 输入数据 X
  • 计算 $A=\sigma (w^{T}X+b)=(a^{(0)},a^{(1)},...,a^{(m-1)},a^{(m)})$
  • 计算成本函数：$J=-\frac{1}{m}{\sum }_{i=1}^m{y}^{(i)}\log (a^{(i)})+(1-y^{(i)})\log (1-a^{(i)})$
• 反向传播，计算梯度
  $$\frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T\text{\hspace{1em}(7)}$$
  $$\frac{\partial J}{\partial b}=\frac{1}{m}\sum _{i=1}^m(a^{(i)}-y^{(i)})\text{\hspace{1em}(8)}$$

• 通过最小化成本函数 $J$ 来学习 $w$ 和 $b$。对于参数 $\theta$，更新规则为 $\theta =\theta -\alpha d\theta$，其中 $\alpha$ 是学习率。

2. 两层的Logistic神经网络（加上输入层是三层）

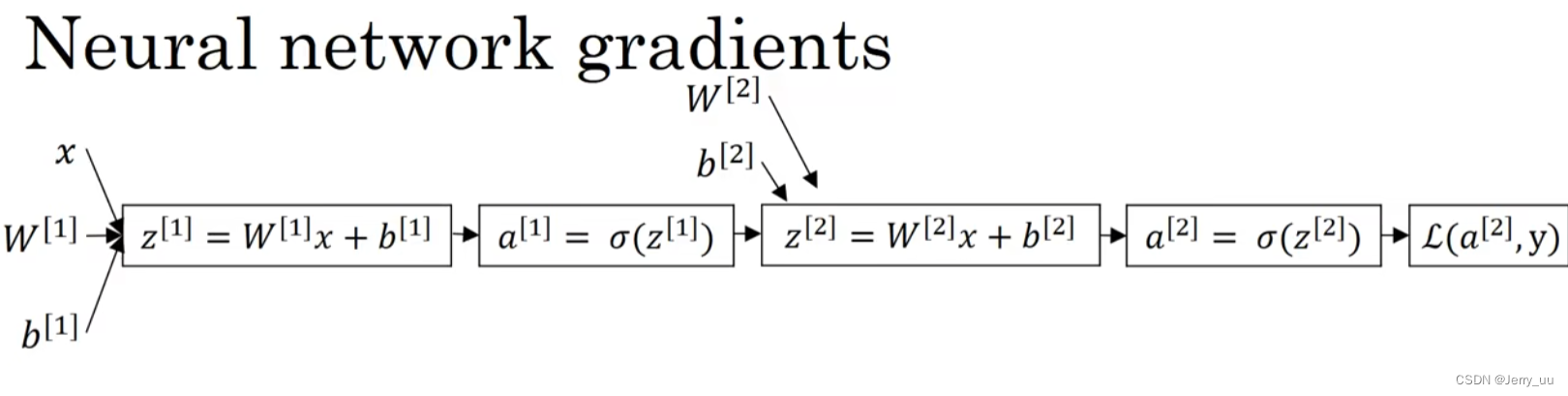
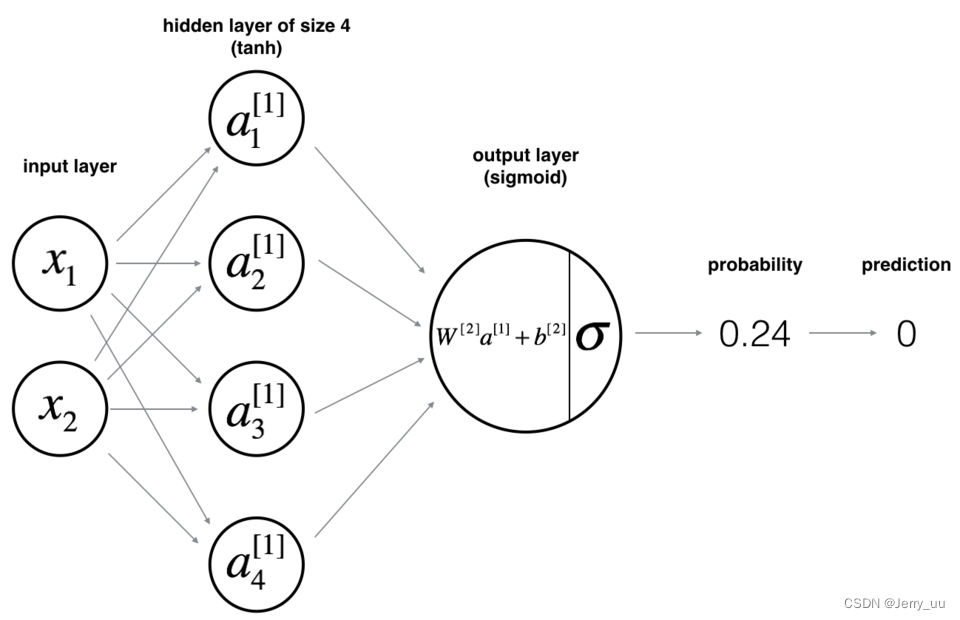
对于一个样本 $x^{(i)}$:

$$z^{[1](i)}=W^{[1]}{x}^{(i)}+b^{[1](i)}\text{\hspace{1em}(8)}$$

$$a^{[1](i)}=\tanh (z^{[1](i)})\text{\hspace{1em}(9)}$$

$$z^{[2](i)}=W^{[2]}{a}^{[1](i)}+b^{[2](i)}\text{\hspace{1em}(10)}$$

$${\hat{y}}^{(i)}=a^{[2](i)}=\sigma (z^{[2](i)})\text{\hspace{1em}(11)}$$

$$y_{\text{prediction}}^{(i)}=\{\begin{array}{ll}1& \text{if }{a}^{[2](i)}>0.5\\ 0& \text{otherwise}\end{array}\text{\hspace{1em}(12)}$$

给定所有样本的预测值，你也可以计算代价 $J$ 如下：

$$J=-\frac{1}{m}\sum _{i=0}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)\text{\hspace{1em}(13)}$$
对于多个样本

2.1 定义神经网络结构

• n_x: the size of the input layer
• n_h: the size of the hidden layer (set this to 4)
• n_y: the size of the output layer

函数名称：layer_sizes
参数：

参数	描述	形状
X	输入数据集	(输入层大小, 样本数)
Y	标签	(输出层大小, 样本数)

返回值：

变量	描述
n_x	输入层的大小
n_h	隐藏层的大小
n_y	输出层的大小

def layer_sizes(X, Y):
    # size of input layer
    n_x = X.shape[0]
    n_h = 4
    n_y = Y.shape[0]
    # size of output layer
    return (n_x, n_h, n_y)

2.2 初始化模型参数（随机初始化）

函数名称：initialize_parameters
参数：

参数	描述	形状
n_x	输入层的大小	-
n_h	隐藏层的大小	-
n_y	输出层的大小	-

返回值：

变量	描述	形状
params	包含参数的 Python 字典	-
W1	第一层权重矩阵	(n_h, n_x)
b1	第一层偏置向量	(n_h, 1)
W2	第二层权重矩阵	(n_y, n_h)
b2	第二层偏置向量	(n_y, 1)

def initialize_parameters(n_x, n_h, n_y):

    np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
    
    W1 = np.random.randn(n_h,n_x) * 0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h) * 0.01
    b2 = np.zeros((n_y,1))
    
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

2.3 优化器

2.3.1 前向传播

函数名称：forward_propagation
参数：

参数	描述	形状
X	输入数据	(n_x, m)
parameters	包含参数的 Python 字典	-

返回值：

变量	描述	形状
A2	第二层激活函数的 S 型输出	(n_y, m)
cache	包含 “Z1”、“A1”、“Z2” 和 “A2” 的字典	-

def forward_propagation(X, parameters):
    
    # Retrieve each parameter from the dictionary "parameters"
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # Implement Forward Propagation to calculate A2 (probabilities)
    Z1 = np.dot(W1,X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1) + b2
    A2 = sigmoid(Z2)
    
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

现在您已经计算了$A^{[2]}$（在 Python 变量 A2 中），它包含了每个样本的 $a^{[2](i)}$，您可以按照以下公式计算代价函数：

$$J=-\frac{1}{m}\sum _{i=0}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)\text{\hspace{1em}(14)}$$

2.3.2 计算损失

函数名称：compute_cost
描述：

计算方程（14）中给定的交叉熵成本。

参数：

参数	描述	形状
A2	第二层激活函数的 S 型输出	(1, 样本数)
Y	“真实” 标签向量	(1, 样本数)
parameters	包含参数 W1、b1、W2 和 b2 的 Python 字典	-

返回值：

变量	描述	形状
cost	根据方程（13）给定的交叉熵成本	数值

def compute_cost(A2, Y, parameters):
   
    m = Y.shape[1] # number of example
    
    # Compute the cross-entropy cost
    logprobs = np.multiply(np.log(A2),Y)+np.multiply(np.log(1-A2),(1-Y))
    cost = - 1/m*np.sum(logprobs)
    
    cost = np.squeeze(cost)     # makes sure cost is the dimension we expect. 
                                # E.g., turns [[17]] into 17 
        
    cost = float(cost)         # without it, type error
    assert(isinstance(cost, float))
    
    return cost

2.3.3 反向传播

反向传播通常是深度学习中最困难（最数学化）的部分。为了帮助您，这里再次提供了关于反向传播的讲座幻灯片。由于您正在构建向量化实现，因此您将需要使用此幻灯片右侧的六个公式。

• 对于第二层的 $z$ 值的偏导数：
  $\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}=\frac{1}{m}(a^{[2](i)}-y^{(i)})$

• 对于第二层权重 $W_2$ 的偏导数：
  $\frac{\partial \mathcal{J}}{\partial W_2}=\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}{a}^{[1](i)T}$

• 对于第二层偏置 $b_2$ 的偏导数：
  $\frac{\partial \mathcal{J}}{\partial b_2}={\sum }_i\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}$

• 对于第一层的 $z$ 值的偏导数：
  $\frac{\partial \mathcal{J}}{\partial z_1^{(i)}}=W_2^T\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}\ast (1-a^{[1](i)2})$

• 对于第一层权重 $W_1$ 的偏导数：
  $\frac{\partial \mathcal{J}}{\partial W_1}=\frac{\partial \mathcal{J}}{\partial z_1^{(i)}}{X}^T$

• 对于第一层偏置 $b_1$ 的偏导数：
  $\frac{\partial {\mathcal{J}}_i}{\partial b_1}={\sum }_i\frac{\partial \mathcal{J}}{\partial z_1^{(i)}}$

请注意，星号 ( * ) 表示元素级乘法。

在深度学习编码中常用的符号包括：

• dW1 = $\frac{\partial \mathcal{J}}{\partial W_1}$
• db1 =$\frac{\partial \mathcal{J}}{\partial b_1}$
• dW2 = $\frac{\partial \mathcal{J}}{\partial W_2}$
• db2 =$\frac{\partial \mathcal{J}}{\partial b_2}$

提示：

• 要计算 $dZ1$，您需要计算 $g^{[1{]}^{\prime }}(Z^{[1]})$。由于 $g^{[1]}(.)$ 是 tanh 激活函数，如果 $a=g^{[1]}(z)$，那么 $g^{[1{]}^{\prime }}(z)=1-a^2$。因此，您可以使用 (1 - np.power(A1, 2)) 来计算 $g^{[1{]}^{\prime }}(Z^{[1]})$。

函数名称：backward_propagation

描述：

根据上述说明实现反向传播。

参数：

参数	描述	形状
parameters	包含参数的 Python 字典	-
cache	包含 “Z1”、“A1”、“Z2” 和 “A2” 的字典	-
X	输入数据	(2, 样本数)
Y	“真实” 标签向量	(1, 样本数)

返回值：

变量	描述	形状
grads	包含关于不同参数的梯度的 Python 字典	-

def backward_propagation(parameters, cache, X, Y):
    
    m = X.shape[1]
    
    # First, retrieve W1 and W2 from the dictionary "parameters".
    W1 = parameters["W1"]
    W2 = parameters["W2"]
        
    # Retrieve also A1 and A2 from dictionary "cache".
    A1 = cache["A1"]
    A2 = cache["A2"]
    # Z1 = cache.get('Z1')
    
    # Backward propagation: calculate dW1, db1, dW2, db2. 
    dZ2 = A2 - Y
    dW2 = 1/m*np.dot(dZ2,A1.T)
    db2 = 1/m*np.sum(dZ2,axis=1,keepdims=True)
    dZ1 = np.dot(W2.T,dZ2) * (1-np.power(A1,2))
    dW1 = 1 / m * np.dot(dZ1,X.T) 
    db1 = 1/m*np.sum(dZ1,axis=1,keepdims=True)
    # it's not Z1, g(z1)' = （1 - A1^2)
        
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

2.3.4 更新参数

函数名称：update_parameters

描述：

使用上述梯度下降更新规则更新参数。

参数：

参数	描述	形状
parameters	包含参数的 Python 字典	-
grads	包含梯度的 Python 字典	-

返回值：

变量	描述	形状
parameters	包含更新后参数的 Python 字典	-

def update_parameters(parameters, grads, learning_rate = 1.2):

    # Retrieve each parameter from the dictionary "parameters"
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # Retrieve each gradient from the dictionary "grads"
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    
    # Update rule for each parameter
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

2.4 集成

函数名称：nn_model

描述：

构建并训练神经网络模型。

参数：

参数	描述	形状
X	数据集	(2, 样本数)
Y	标签	(1, 样本数)
n_h	隐藏层的大小	-
num_iterations	梯度下降迭代次数	-
print_cost	如果为 True，则每 1000 次迭代打印成本	-

返回值：

变量	描述	形状
parameters	模型学到的参数，可以用于预测	-

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
  
    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # Loop (gradient descent)

    for i in range(0, num_iterations):
         
        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        A2,cache = forward_propagation(X, parameters)
        
        # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
        cost = compute_cost(A2, Y, parameters)
        
        # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        grads = backward_propagation(parameters, cache, X, Y)
        
        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        parameters = update_parameters(parameters, grads, learning_rate = 1.2)
        
        # Print the cost every 1000 iterations
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
            
    return parameters