slam中的数学知识

Ax=b的解问题：

（i）无解的充分必要条件是 R（A）＜R（A，b）；

（ii）有惟一解的充分必要条件是 R（A）= R（A，b）= n；

（iii）有无限多解的充分必要条件是 R（A）= R（A，b）＜n.

R值矩阵的秩，行列的极大线性无关组的数量

列空间维度，行空间维度，就是指行秩和列秩

基础解系等同于特征向量，特征值不相等，对应特征向量线性无关

 A 与 B 相似，即有可逆矩阵 P，使 P -1 A P = B，特征值相同，特征向量也相同

n 阶矩阵 A 与对角矩阵相似（即 A 能对角化）的充分必要条件是 A 有 n 个线性无关的特征向量

如果 n 阶矩阵 A 的 n 个特征值互不相等，则 A 与对角矩阵相似

线性无关不代表正交

对称矩阵的特征值为实数.

设λ1，λ2 是对称矩阵 A 的两个特征值，p1，p2 是对应的特征向量. 若λ1≠λ2，则 p1 与 p2 正交.

设 A 为 n 阶对称矩阵，则必有正交矩阵 P，使 P -1 A P = P T A P =Λ，其 中Λ 是以 A 的 n 个特征值为对角元的对角矩阵.

设 A 为 n 阶对称矩阵，λ是 A 的特征方程的 k 重根，则矩阵 A -λE 的 秩 R（A -λE）= n-k，从而对应特征值λ恰有 k 个线性无关的特征向量.

二次型与对称矩阵之间存在一一对应的关系

二次型f=x 2 -3z 2 -4xy+yz  对称矩阵A的秩就叫做二次型f的秩

任给一个二次型，就惟一地确定一个对称矩阵；反之，任给一个对称矩阵，也可惟一地确定一个二次型  二次型与对称矩阵之间存在一一对应的关系.

我们把对称矩阵A叫做二次型f的矩阵，也把f叫做对称矩阵A的二次 型.对称矩阵A的秩就叫做二次型f的秩.

线性代数——二次型 - 知乎 (zhihu.com)

任给二次型 ，总有正交变换 x = Py，使f化为标准形

 其中λ1，λ2，…，λn 是f的矩阵 A =（aij）的特征值

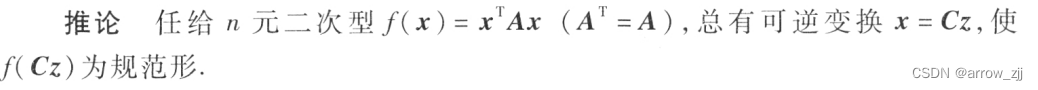
 n 元二次型f=x T A x 为正定的充分必要条件是：它的标准形的 n 个 系数全为正，即它的规范形的 n 个系数全为 1，亦即它的正惯性指数等于 n.

对称矩阵 A 为正定的充分必要条件是：A 的特征值全为正.

对称矩阵 A 为正定的充分必要条件是：A 的各阶主子式都为正

正定矩阵，首先要求是对称矩阵

二次型，存在对应方程全在零向量上和零向量上下都有的问题

1. 指数函数是凸函数；
2. 对数函数是凹函数，然后负对数函数就是凸函数；
3. 对于一个凸函数进行仿射变换，可以理解为线性变换，结果还是凸函数；
4. 二次函数是凸函数（二次项系数为正）；
5. 高斯分布函数是凹函数；
6. 多个凸函数的线性加权，如果权值是大于等于零的，那么整个加权结果函数是凸函数。

(18条消息) 机器学习中关于判断函数凸或凹以及最优化的问题_Orange先生的博客-CSDN博客_凹优化

矩阵就是线性变化，通过线性变化不改变函数的凹凸性，对二次型矩阵标准化，通过标准化后的二次型，判断函数的凹凸性，就是原函数的凹凸性；

梯度下降抖动，走锯齿路线，二阶牛顿法，H矩阵难以求解

高斯牛顿法：e(x)=真值-估计值，将e(x)进行一阶泰勒展开，不是常见的目标函数

正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。

对称矩阵的正定性，半正定，负定性与该对称矩阵特征值的关系是： 矩阵的正定当且仅当其特征值都大于0； 矩阵的半正定当且仅当其特征值都大于或等于0； 矩阵的负定当且仅当其特征值都小于0

判定矩阵正定性的意义：

如何理解正定矩阵和半正定矩阵 - 知乎 (zhihu.com)

(19条消息) 《视觉SLAM十四讲 第二版》笔记及课后习题（第六讲）_nullwh的博客-CSDN博客

凸函数具有全局最大值，凹函数具有全局最小值

矩阵正定，等价于标量空间中y=ax^2,a大于零，整个系统具有全局最小值

从系统角度看，如果一个矩阵是正定的，那么我们可以简单理解这个系统拥有全局最小值

比如如果矩阵二阶导为正定矩阵xtAx > 0，则证明其具有局部最小值解，比如协方差矩阵，动力矩阵都是正定的。仅需要判定二次项的系数矩阵的正定性即可得到矩阵方程的求解问题

对于上述方程来说：JT.J相当于二次型矩阵，代表了系统的整体收敛状态，实际数据中该矩阵为半正定状态，不稳定，容易导致算法不收敛。同时求解出来的增量有可能太大，导致采用的不准确。局部近似

是半正定的，当 J 为零向量时，不正定。此时几何含义是代价函数在此点平坦，导数为0、这种情况下局部的近似为一条水平直线，无法确定参数的更新方向使代价下降，不稳定，同时求解出来的增量不准确甚至很大 所以非线性优化求极值时，尽量要求矩阵为正定矩阵。

Levenberg-Marquadt方法：通过近似模型和实际模型之间的差距来确定信赖区域的范围

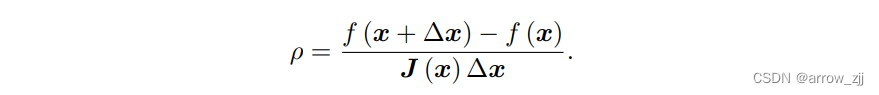
接近于1，近似较好，远大于1，效果好，可以扩大搜索范围，远小于1，实际下降的相较于预期要小，效果差，缩小范围 

系数D通常取为二次雅可比矩阵的对角元素平方根，以使得梯度小的其可操作空间更大一些

拉格朗日将有约束问题转化为无约束问题

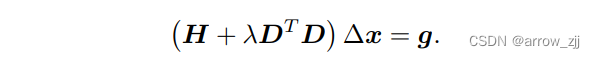
 权衡二次和一次，牛顿法和最速下降法，在一定程度上避免系数矩阵的非奇异和病态问题，提供更稳定的增量

ps:范数对于向量而言的，1范数，向量元素绝对值之和，2范数，向量元素绝对值之和在开方

Line search Trust Region 两种方法

初始值的选取：通过ICP，PnP之类的算法提供优化初始值

线性方程的求解（得到增量的结果）：QR、Cholesky

通常会利用系数矩阵的稀疏形式，进行分解，最后求解