深度强化学习：Actor-Critic、A2C、A3C

深度强化学习算法：Actor-Critic、A2C、A3C

1. Actor-Critic

强化学习算法有policy-based和value-based，那么可以构造两个神经网络以达到既可以学习价值函数，又可以学习策略函数吗？当然可以，这就是Actor-Critic算法了。

在REINFORCE算法中，使用Monte Carlo方法来估计$Q(s,a)$，那么在Actor-Critic中，可以把Monte Carlo方法换成神经网络来估计价值函数。Actor-Critic算法本质上是基于策略的算法，因为它的目标是优化一个带参数的策略，只是会额外学习价值函数，从而帮助策略函数更好地学习。在策略梯度中，我们可以把梯度写成下面这个更加一般的形式：
$$g=E[\sum _{t=0}^T{\varphi }_t{\nabla }_{\theta }log{\pi }_{\theta }(a_t,s_t)]\text{\hspace{1em}(1)}$$
其中，${\varphi }_t$可以有很多种形式：

这些形式都可以用，是因为它们本质上都是对回报的不同估计或重构，理论上等价，但实际效果因偏差与方差的权衡而不同。选择哪种形式取决于具体的任务需求和优化目标，直接回报（总回报1或动作后回报2）最直观，但是方差较高；基准线方法（形式3）可以减少方差，提升训练稳定性；价值函数方法（形式4）通过神经网络逼近的方式估算价值，提高了计算效率，但很依赖于估计精度；优势函数方法（形式5）衡量了当前动作价值相对于平均值都有优越程序，通过优越函数，策略优化可以更加集中在动作的相对改进上，而不是绝对值上；时序差分方法（形式6）是优势函数的一步估计形式，即时序差分残差可以看作优势函数值的估计值，但是仅限于一步估计，因为采取动作和状态转移都是概率分布，优势函数是求动作价值与状态价值的差的期望，而形式6是用一步采样的方式来对期望进行估计。另外，状态价值$V(S_t)$的值通常由神经网络函数逼近给出，如果逼近器不准确，也会导致偏差。

这里以形式4来讲解Actor-Critic，之后形式5会在A2C部分讲解。

下面来具体讲解Actor-Critic算法。

策略梯度方法用策略梯度${\nabla }_{\theta }J(\theta )$更新策略网络参数$\theta$，从而增大目标函数。策略梯度${\nabla }_{\theta }J(\theta )$的无偏估计，即下面的随机梯度：
$$g(s,a;\mathbf{\theta })\triangleq Q_{\pi }(s,a)\cdot {\nabla }_{\theta }\ln \pi (a\mid s;\mathbf{\theta })\text{\hspace{1em}(2)}$$
由于其中的动作价值函数$Q_{\pi }$是未知的，所以无法直接计算$g(s,a;\mathbf{\theta })$。这里用神经网络（形式4）来近似$Q_{\pi }$。

Actor-Critic 方法用一个神经网络近似动作价值函数$Q_{\pi }(s,a)$，这个神经网络叫作“价值网络”，记为$q(s,a;\mathbf{w})$，其中的$\mathbf{w}$表示神经网络中可训练的参数。价值网络的输入是状态$s$，输出是每个动作的价值。动作空间$A$中有多少中动作，那么价值网络的输出就是多少维的向量，向量每个元素对应一个动作。

虽然价值网络$q(s,a;\mathbf{w})$与DQN有相同的结构，但是两者的意义不同，训练算法也不同。价值网络是对动作价值函数$Q_{\pi }(s,a)$的近似。而DQN则是对最优动作价值函数$Q_{\star }(s,a)$的近似。对价值网络的训练使用的是SARSA算法，它属于是同策略，不能用经验回放(experience replay)。对DQN的训练使用的是Q学习算法，它属于异策略，可以用经验回放。

Actor-Critic 可以翻译成“演员-评论员”方法。策略网络$\pi (a|s;\mathbf{\theta })$相当于演员，它基于状态$s$，做出动作$a$。价值网络$q(s,a;\mathbf{w})$相当于评论员，他给演员的表现打分，评价在状态$s$的情况下做出动作$a$的好坏程度。策略网络（演员）和价值网络（评论员）的关系如下图所示。

对于上图，为什么不直接把奖励R反馈给策略网络（演员），而要用价值网络（评论员）这样一个中介呢？是因为，策略学习的目标函数$J(\theta )$是回报U的期望，而不是奖励R的期望。虽然能观测到当前的奖励R，但是它对策略网络是毫无意义的。训练策略网络（演员）需要的是回报U，而不是奖励R。价值网络（评论员）能够估算出回报U的期望，因此能帮助训练策略网络（演员）。

那么如何训练策略网络（演员）呢？

我们要明白，策略网络（演员）想要改进自己的performence，但是演员自己并不知道怎样的performence才是好的，怎样的performence才是不好的，所以需要价值网络（评论员）的帮助。在演员做出动作 $a$ 之后，评论员会打一个分数$\hat{q}\triangleq q(s,a;\mathbf{w})$，并把分数反馈给演员，帮助演员做出改进。演员利用当前的状态 $s$ ，自己的动作 $a$ ，以及评论员的打分 $\hat{q}$，计算近似策略梯度，然后更新自己的参数 $\mathbf{\theta }$。通过这种方式，演员的表现越来越受评论员的好评，于是演员获得的评分 $\hat{q}$ 越来越高。演员并不一定是朝着表现更好的方向发展，它是朝着评论员给出的更高的分数发展，至于是不是向着表现更好地方向发展取决于评论员的“评赏能力”了，如果评论员随意打分，演员的表现当然不会越来越好。

训练策略网络的基本想法是用策略梯度 ${\nabla }_{\theta }J(\theta )$ 的近似来更新参数 $\theta$ 。再来看式(2)，策略梯度的无偏估计：
$$g(s,a;\mathbf{\theta })\triangleq Q_{\pi }(s,a)\cdot {\nabla }_{\theta }\ln \pi (a\mid s;\mathbf{\theta })$$
价值网络 $q(s,a;\mathbf{\theta })$ 是对动作价值函数 $Q_{\pi }(s,a)$ 的近似，所以把上面公式中的 $Q_{\pi }$ 替换成价值网络，得到近似策略梯度：
$$\hat{g}(s,a;\mathbf{w})\triangleq q(s,a;\mathbf{w})\cdot {\nabla }_{\theta }\ln \pi (a|s;\mathbf{\theta })\text{\hspace{1em}(3)}$$
$q(s,a;\mathbf{w})$ 是评论员给出的分数。

最后做梯度上升更新策略网络的参数：
$$\theta \leftarrow \theta +\beta \cdot \hat{g}(s,a;\mathbf{\theta })\text{\hspace{1em}(4)}$$

解释一下为什么使用上述方式更新参数之后会让评论员打出的分数越来越高：状态价值函数 $V_{\pi }(s)$ 可以近似成为：
$$v(s;\mathbf{\theta })=E_{A\sim \pi (\cdot |s;\mathbf{\theta })}[q(s,A;\mathbf{w})]\text{\hspace{1em}(5)}$$
因此可以将 $v(s;\mathbf{\theta })$ 看作评论员打分的均值。那么公式(3)中定义的近似策略梯度$\hat{g}(s,a;\mathbf{\theta })$ 的期望等于 $v(s;\mathbf{\theta })$ 关于 $\mathbf{\theta }$ 的梯度：
$${\nabla }_{\theta }v(s;\mathbf{\theta })=E_{A\sim \pi (\cdot |s;\mathbf{\theta })}[\hat{g}(s,A;\mathbf{\theta })]\text{\hspace{1em}(6)}$$
因此，用公式(4)中的梯度上升更新 $\mathbf{\theta }$ ，会让 $v(s;\mathbf{\theta })$ 变大，也就是让评论员打分的均值更高。

策略网络的训练就是以上的方式，接下来是价值网络（评论员）的训练。

上面已经提到训练策略网络（演员）的方法不是真正让演员表现更好，只是让演员更加迎合评论员的喜好而已。因此，评论员的水平也很重要，只有当评委的打分 $\hat{q}$ 真正反映出动作价值 $Q_{\pi }$ ，演员的水平才能真正提高。初始的时候，价值网络的参数 $\mathbf{w}$ 是随机的，也就是说评委的打分就是瞎给分。可以用 SARSA 算法更新 $\mathbf{w}$，提高评委的水平。每次从环境中观测到一个奖励 $r$ ，把 $r$ 看做是真相，用 $r$ 来校准评委的打分。

关于 SARSA 算法，在 t 时刻，价值网络输出 $\hat{q}(s_t,a_t;\mathbf{w})$ ，它是对动作价值函数 $Q_{\pi }(s_t,a_t)$ 的估计。在 $t+1$ 时刻，实际观测到 $r_t,s_{t+1},a_{t+1}$ ，于是可以计算 TD target :
$${\hat{y}}_t\triangleq r_t+\gamma \cdot q(s_{t+1},a_{t+1};\mathbf{w})\text{\hspace{1em}(7)}$$
它也是对动作价值函数 $Q_{\pi }(s_t,a_t)$ 的估计。由于 $\hat{y}$ 部分基于实际观测到的奖励 $r_t$ ，$\hat{y}比q(s_t,a_t;\mathbf{w})$更接近事实真相。所以把 $\hat{y}$ 固定住，鼓励 $q(s_t,a_t;\mathbf{w})$ 去接近 $\widehat{y_t}$ 。SARSA 算法具体这样更新价值网络参数 $\mathbf{w}$ 。定义损失函数：
$$L(w)\triangleq \frac{1}{2}[q(s_t,a_t;\mathbf{w})-\widehat{y_t}{]}^2\text{\hspace{1em}(8)}$$
设 $\hat{q}\triangleq q(s_t,a_t;\mathbf{w})$ 。损失函数的梯度是：
$${\nabla }_{w}L(w)=(\widehat{q_t}-\widehat{y_t})\cdot {\nabla }_{w}q(s_t,a_t;\mathbf{w})\text{\hspace{1em}(9)}$$
然后做梯度下降更新 $\mathbf{w}$：
$$\mathbf{w}\leftarrow \mathbf{w}-\alpha \cdot {\nabla }_{w}L(w)\text{\hspace{1em}(10)}$$
这样更新 $\mathbf{w}$ 可以让 $q(s_t,a_t;\mathbf{w})$ 更接近 $\widehat{y_t}$ 。可以这样理解 SARSA :用观测到的奖励 $r_t$ 来“校准”评论员的打分 $q(s_t,a_t;\mathbf{w})$ 。

接下来看下 Actor-Critic 完整的训练流程。设当前策略网络参数是 ${\theta }_{now}$ ，价值网络参数是 $w_{now}$ 。 下图是Actor-Critic的训练流程以及用目标网络 $q(s,a;{\mathbf{w}}^{-})$来改进训练以缓解 SARSA 算法中的自举带来的高估偏差。

2. Advantage Actor-Critic (A2C)

如果估计使用优势函数（形式5），那么就是 A2C 。

在第1节中，Actor-Critic 使用 $Q(s,a;\mathbf{w})$ 价值函数来估计，在这里我们用带基线的策略梯度，关于策略梯度的一个无偏估计：
$$g(s,a;\mathbf{\theta })=[Q_{\pi }(s,a)-V_{\pi }(s)]\cdot {\nabla }_{\theta }\ln \pi (a|s;\mathbf{\theta })\text{\hspace{1em}(11)}$$
其中的 $Q_{\pi }(s,a)-V_{\pi }(s)$ 被称为优势函数（advantage function）。基于此公式得到的 Actor-Critic 方法被称为 Advantage Actor-Critic ，缩写 A2C 。

A2C 属于 Actor-Critic 方法的一种，有一个策略网络 $\pi (a|s;\mathbf{\theta })$ ，相当于演员，用于控制智能体运动。还有一个价值网络 $v(s;\mathbf{w})$ ，相当于评论员，他的评分可以帮助策略网络（演员）改进其 performence 。两个神经网络的结构与上一节中的完全相同，但是本节和上一节用不同的方法来训练两个神经网络。

A2C 中策略网络（演员）和价值网络（评论员）的关系如下图所示。智能体由策略网络 $\pi$ 控制，与环境交互，并收集状态、动作、奖励。策略网络（演员）基于状态 $s_t$ 做出动作 $a_t$ 。价值网络（评论员）基于 $s_t、s_{t+1}、r_t$ 算出 TD 误差 ${\delta }_t$ 。策略网络（演员）依靠 ${\delta }_t$ 来判断自己动作的好坏，从而改进自己的演技（即参数 $\mathbf{\theta }$）。

可能你会有疑问：价值网络 $v$ 只知道两个状态 $s_t、s_{t+1}$ ，而并不知道动作 $a_t$ ，那
么价值网络为什么能评价 $a_t$ 的好坏呢？价值网络 $v$ 告诉策略网络 $\pi$ 的唯一信息是 ${\delta }_t$ 。回顾一下 ${\delta }_t$ 的定义：
$$\begin{array}{rcl}-{\delta }_t& =& \underset{\text{TD 目标}{\hat{y}}_t}{\underbrace{r_t+\gamma \cdot v\left(s_{t+1};\mathbf{w}\right)}}-\underset{\text{基线}}{\underbrace{v\left(s_t;\mathbf{w}\right)}}.\end{array}\text{\hspace{1em}(12)}$$
基线 $v(s_t;w)$ 是价值网络在 $t时刻对E[U_t]$ 的估计；此时智能体尚未执行动作 $a_t$ 。而 TD 目标 $\widehat{y_t}$ 是价值网络在 $t+1时刻对E[U_t]$ 的估计；此时智能体已经执行动作 $a_t$ ，也就是 $\widehat{y_t}$ 已经包含了动作 $a_t$ 的影响。

这也是 A2C 相比与原始 Actor-Critic 的优势所在，不需要估计两个价值函数，只需要估计$v(s;\mathbf{w})$ ，而不需要估计动作价值函数 $Q_{\pi }$ 了，用V来表示 Q 的值，当然，策略网络也是需要估计的，这里不讨论策略网络。虽然这里引入了 $r$ ，并且 $r$ 是有随机性的，但是相较于回报 U 是一个较小的值，因为 $r$ 是某一个步骤得到的奖励，而 U 是所有未来会得到的奖励的总和， U 的方差较大。 $r$ 虽然也有一些方差，但是它的方差比 U 的要小。至于为什么第1节中仅有Q，没有V，是因为其并没有用到基线，这里用到了优势函数并将 V 作为其基线。

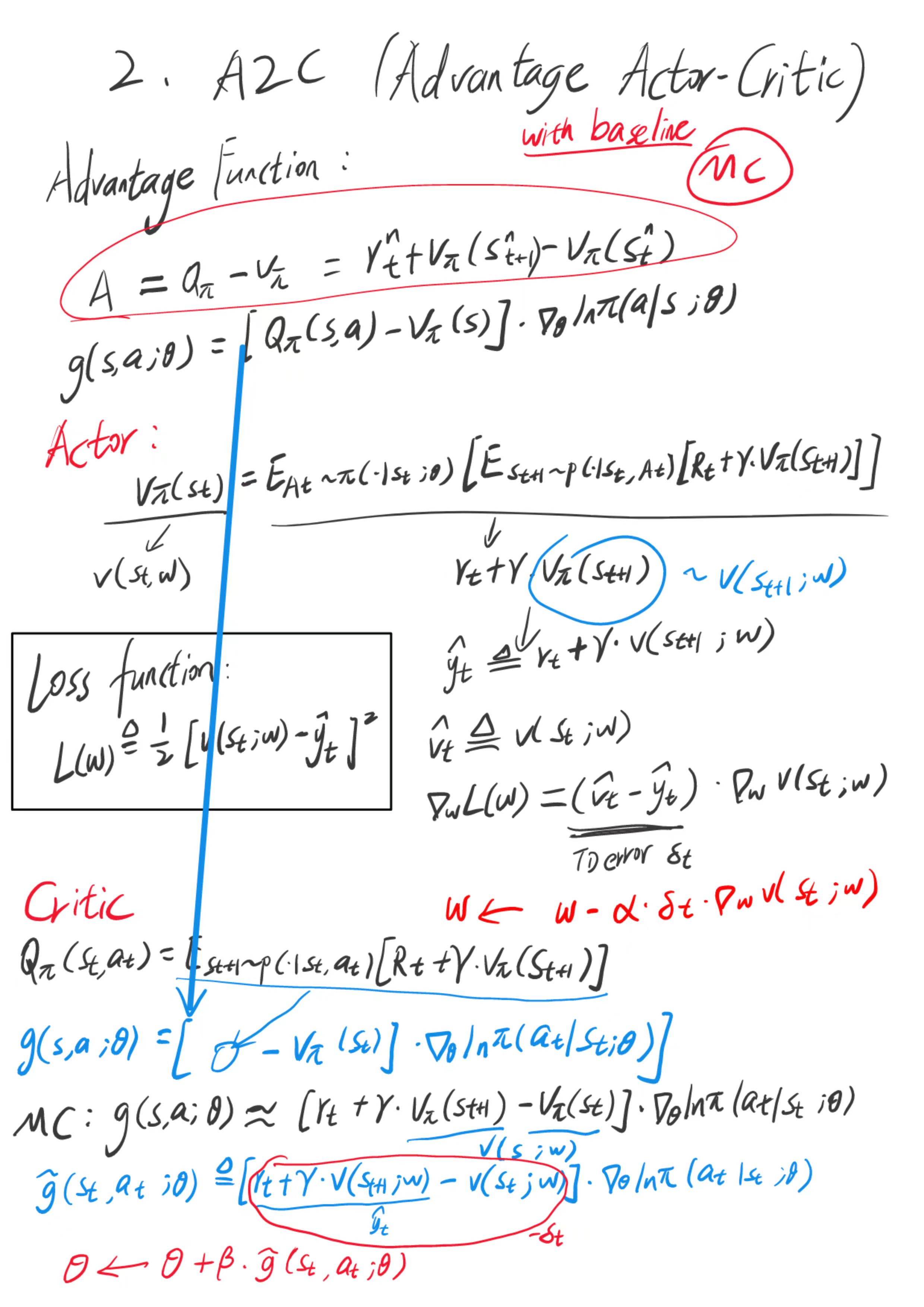
以下是训练的具体流程：

3. Asynchronous Advantage Actor-Critic (A3C)

A3C 即异步优势演员-评论员算法，主要的特点是同时使用很多个进程(worker)，每一个进程就像一个分身，最后这些分身会把所有的经验值集合在一起。

参考：
1.王树森老师的书《深度强化学习》
2.张伟楠老师的书《动手学强化学习》
3.李宏毅老师的课程的文字整理《强化学习教程》