【机器人运动学】——刚体运动的描述

【机器人运动学】——刚体转动的拆解

一、转动

1. 物体转动的注意事项：

（1）多次转动需要确定先后顺序，转动顺序不能互换。

（2）旋转的转轴需要确定清楚。

2. 物体转动R的两种拆解方式

（1）对方向固定不动的转轴：FIxed angles （XYZ）→ 左乘基

• 注意1：由旋转矩阵R也可以推算出旋转角度。
• 注意2：式子乘个P，就更直观了。先操作x，之后结果再操作y，结果再操作z。

（2）对转动的frame当下的转轴：Euler angles （ZYX）→ 右乘联体

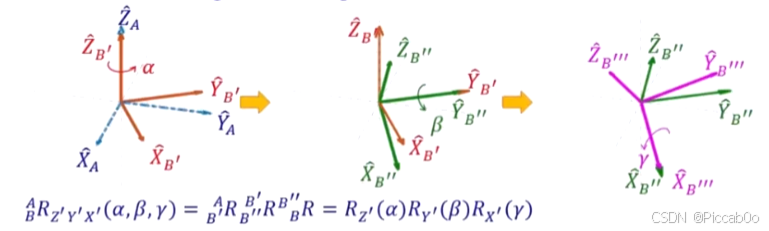
• 注意1：这里可以这么想，把一个向量先mapping（转换）到第一个frame，再到第二个，再到第三个。那么相当于，整体是从最后一个mapping回来的，只有这样才能保证两种拆解方式得到的结果一致。
• 注意2：这也就说明Fixed angle的正转和Euler angle的反转可以得到一样的解。

（3）对转动的frame当下的转轴，也可以利用ZYZ的方式进行拆解。

二、刚体运动状态的表达

1. 齐次变换矩阵T：将姿态和位置统一起来。

$${}_B^{A}T=\left[\begin{array}{cccc}-& {}_B^{A}R& -& {}^A{P}_{Borg}\\ 0& 0& 0& 1\end{array}\right]$$

2. 对于齐次变换矩阵T而言，其也可以用于描述frame间的变换mapping情况（相对空间状态），也可以用于向量/点的移动转动操作operate。

• 注意1：这里的齐次变换，应该是先转动再移动。
• 注意2：很容易想，点和向量的移动和转动，相当于基frame的反动和反转。

3. 齐次变换矩阵的运算：

（1）连续运算：ABC系联乘

（2）反矩阵：由${}_B^{A}T{}_A^{B}T=I_{4\times 4}$可得，

（3）B对A的转轴旋转：premultiply，左乘

（4）B对B的转轴旋转：postmultiply，右乘