【现代控制理论笔记】——第三章：状态反馈

现代控制理论

第三章

说明：

介绍了状态反馈的形式，以及引入状态反馈配置极点的问题，进一步引出镇定问题

其中可能涉及到四阶行列式的计算，可以用“$\Sigma$矩阵某一行元素*代数余子式”的方法算。

1. 状态反馈

对系统：

$$\begin{gathered} \dot{x}=Ax+Bu \\ y=Cx \end{gathered}$$

引入状态正反馈：

$u=Kx+v$

得到状态反馈系统：

$$\begin{gathered} \dot{x}=(A+BK)x+Bv \\ y=Cx \end{gathered}$$

框图：

可以看出，状态反馈的引入改变了系统矩阵，但不改变能控性：

2. 状态反馈的闭环极点配置问题

目标：

通过状态反馈的引入，改变系统矩阵，使闭环极点定位于目标位置。

状态反馈极点配置的前提：

系统是能控的。

2.1 单输入系统的极点配置步骤：

① 根据A求出原系统的特征多项式：$det(sI-A)=a_0+...+a_{n-1}{s}^{n-1}+s^n$

② 根据闭环极点求出目标多项式：$\alpha (s)={\bar{a}}_0+...+{\bar{a}}_{n-1}{s}^{n-1}+s^n$

③ 求出$\hat{K}=[a_0-{\bar{a}}_0,...,a_{n-1}-{\bar{a}}_{n-1}]$

④ 计算变换矩阵，并求逆$T^{-1}$：

$T=\left[\begin{array}{cccc}{A}^{n-1}b& \cdots & Ab& b\end{array}\right]\left[\begin{array}{cccc}1& & & \\ a_{n-1}& \ddots & & \\ ⋮& \ddots & \ddots & \\ a_1& \cdots & a_{n-1}& 1\end{array}\right]$

⑤ 确定反馈增益矩阵：$K=\hat{K}{T}^{-1}$

2.2 多输入系统的极点配置

情况相对复杂，需要对A进行分类讨论

1）A为循环矩阵时：

2）A不是循环矩阵时：

因此，只要$(A,B)$能控，则一定存在状态反馈使闭环系统$(A+BK,B)$有任意配置的极点。

同时，有：

说明：

对于多输入的系统（其实对于单输入系统也可），其可以采用“偷懒”的方法进行状态反馈配置，思路为：

根据期望配置的极点求出的特征多项式$\alpha (s)=s^4+6s^3+14s^2+16s+8$，我们可以得到期望的系统矩阵$A+BK$为：

$A+BK=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -8& -16& -14& -6\end{array}\right]$

由已知的$(A,B)$可以反求出$K=...$

2.3 状态反馈对传函零点的影响

对于多输入系统整体的零点也不变，但是状态反馈的引入可能改变某一元的零点。

3. 线性定常系统的镇定问题

定义：

对于引入状态反馈的系统，若增益阵$K$使$A+BK$的特征值全部位于左半平面，则称系统是能稳的。

→ 能控，则状态反馈可以任意配置极点，则一定能稳。

→ 需能控分解时，系统特征值是可控和不可控部分的组合，因此：

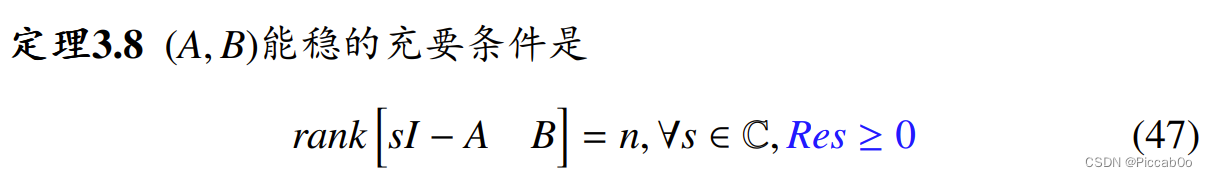
进一步，若系统能通过状态反馈构成的闭环系统，使之渐近稳定（特征值全部位于左半平面），则称是状态反馈可镇定的。