系统稳定性判定分析（四）---- 传递函数前情提要

传递函数前情提要

傅里叶变换与拉普拉斯变换

傅里叶变换的目的是可将时域（即时间域）上的信号转变为频域（即频率域）上的信号，随着域的不同，对同一个事物的了解角度也就随之改变，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理。

拉普拉斯变换可以说是现代工程学使用最广泛的数学工具，它可以通过数学变换将微积分方程转化成代数方程。(重要人物：赫维赛德)

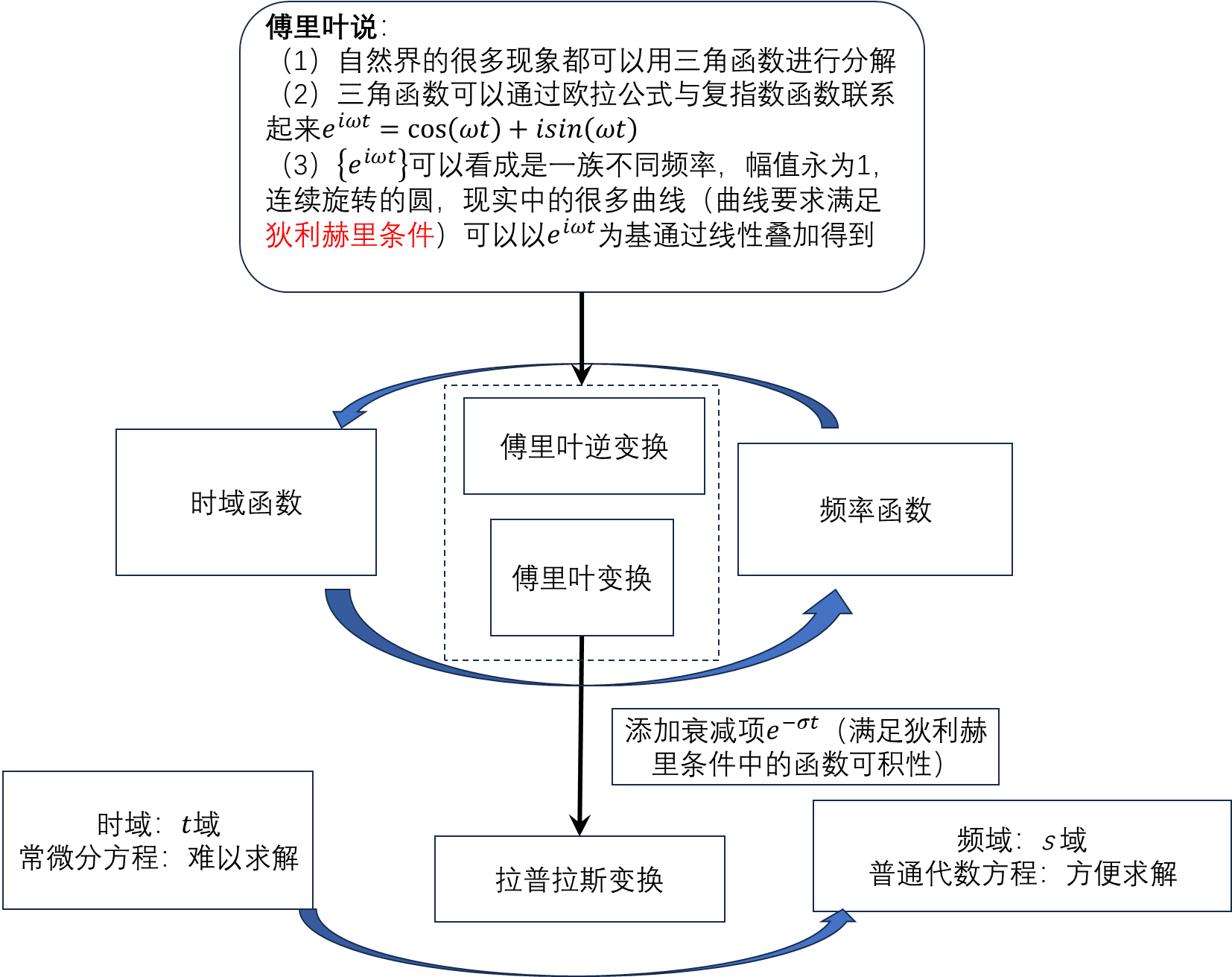
傅里叶定律 只要一个函数满足狄利赫里条件，则其可以分解为复指数函数之和。

狄利赫里条件
(1) 函数在任意有限区间内连续，或只有有限个第一类间断点；
(2) 在一个周期内，函数有有限个极大值或极小值；
(3) 函数$f(t)$绝对可积，即有${\int }_0^{+\infty }|f(t)|dt<\infty$.

当函数$f(t)$满足狄利赫里条件时，其傅里叶变换及其逆变换为：
$$F(\omega )={\int }_{-\infty }^{+\infty }f(t)e^{-i\omega t}dt,\text{\hspace{1em}(1)}$$$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(\omega )e^{i\omega t}d\omega ,\text{\hspace{1em}(2)}$$
添加衰减函数$e^{-\sigma t}$，并将时间域的范围缩减为正半轴，则傅里叶变换变为：
$$F(\omega )={\int }_0^{+\infty }f(t)e^{-\sigma t}{e}^{-i\omega t}dt={\int }_0^{+\infty }f(t)e^{-(\sigma +i\omega )t}dt$$令$s=\sigma +i\omega$，则得拉普拉斯变换
$$F(s)={\int }_0^{+\infty }f(t)e^{-st}dt,\text{\hspace{1em}(3)}$$

线性时不变系统的优点

线性时不变系统是一种特殊的线性系统，其继承了线性系统的叠加性，同时系统的参数不随时间变化，亦即信号作用的前后只影响响应输出的先后而不影响形状。

控制，要求我们精确知道每个时刻系统的状态是什么，而系统当前的状态又由系统的初始状态以及之前所有时刻的输入决定。对于线性系统其满足叠加定理，因此要确定当前时刻系统的状态，我们可以将之前所有时刻的输入带来的当前时刻响应叠加，再加上系统初始状态即可。

卷积

卷积简介与应用

卷积
卷积是在信号与线性系统的基础和背景中出现的，信号与线性系统讨论的就是信号经过一个线性系统以后发生的变化，可以根据需要待处理的信号形式，来设计所谓的系统的传递函数，系统的传递函数与输入信号在数学上的形式就是所谓的卷积关系。利用卷积定理可以将时间域或空间域中的卷积运算等价为频域的相乘运算。

卷积在工程和数学上都有很多应用
如统计学中，加权的滑动平均是一种卷积。概率论中，两个统计独立变量$X$与$Y$的和的概率密度函数是$X$与$Y$的概率密度函数的卷积。光学中，反射光可以用光源与一个反映各种反射效应的函数的卷积表示。带脑子工程与信号处理中，任一个线性系统的输出都可以将输入信号与系统函数做卷积获得。物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

对于一个线性时不变系统，若已知系统的初始状态以及之前所有时刻的输入信号，可通过卷积计算线性时不变系统的任意时刻的输出响应。两函数的卷积定义如下：
$$f_1(t)\ast f_2(t)={\int }_{-\infty }^{+\infty }{f}_1(\tau )f_2(t-\tau )d\tau ,\text{\hspace{1em}(4)}$$其中$f_1(t)\ast f_2(t)$代表函数$f_1(t)$与函数$f_2(t)$的卷积。关于卷积的更多介绍及解释可参见如何通俗易懂地解释卷积下的回答及互动内容。

关于卷积的自我小思想： 假定$f(t)=f_1(t)\ast f_2(t)$表示$t$时刻一植株的生长高度，$f_1(\tau )$表示在$\tau$时刻的生长速度，$f_2(t-\tau )$表示$\tau$时刻植株生长速度对于$t$时刻植株生长高度的影响比重。植株持续性生长，那么植株$t$时刻的生长高度由植株$t$时刻之前的所有时刻的生长速度决定，每一时刻的生长速度对植株$t$时刻的生长高度影响程度不同，其影响程度对应卷积距离，具体表现为: 离得近的信号，卷积距离短；离得远的信号，卷积距离长。

卷积定理

卷积定理是傅里叶变换满足的一个重要性质。卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。具体分为时域卷积定理和频域卷积定理。这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换等各种傅里叶变换的变体同样成立。

定义$\mathcal{F}$表示傅里叶变换，若函数$f_1(t)$的傅里叶变换为${\mathcal{F}}_1(\omega )$, 函数$f_2(t)$的傅里叶变换为${\mathcal{F}}_2(\omega )$，则

时域卷积定理 两信号在时域的卷积积分对应于在频域中该两信号的傅里叶变换的乘积，即有$$\mathcal{F}[f_1(t)\ast f_2(t)]={\mathcal{F}}_1(\omega )\times {\mathcal{F}}_2(\omega ).$$

频域卷积定理 两信号在时域的乘积对应于该两信号傅里叶变换的卷积的傅里叶逆变换除以$2\pi$，即有$$f_1(t)\times f_2(t)=\frac{1}{2\pi }\mathcal{I}\mathcal{F}[{\mathcal{F}}_1(\omega )\ast {\mathcal{F}}_2(\omega )].$$

证明

时域卷积定理证明 已知$\mathcal{F}$为傅里叶变换，则$$\begin{array}{rl}\mathcal{F}[f_1(t)\ast f_2(t)]& ={\int }_{-\infty }^{+\infty }[{\int }_{-\infty }^{+\infty }{f}_1(\tau )f_2(t-\tau )d\tau ]e^{-iwt}dt\\ & ={\int }_{-\infty }^{+\infty }{f}_1(\tau )[{\int }_{-\infty }^{+\infty }{f}_2(t-\tau )e^{-iwt}dt]d\tau \\ & ={\int }_{-\infty }^{+\infty }{f}_1(\tau )e^{-iw\tau }[{\int }_{-\infty }^{+\infty }{f}_2(t-\tau )e^{-iw(t-\tau )}d(t-\tau )]d\tau \\ & ={\int }_{-\infty }^{+\infty }{f}_1(\tau )e^{-iw\tau }{\mathcal{F}}_2(\omega )d\tau \\ & ={\mathcal{F}}_2(\omega ){\int }_{-\infty }^{+\infty }{f}_1(\tau )e^{-iw\tau }d\tau \\ & ={\mathcal{F}}_2(\omega )\times {\mathcal{F}}_1(\omega ).\end{array}$$证毕。

频域卷积定理证明 函数$f_1(t)$的傅里叶变换为${\mathcal{F}}_1(\omega )$, 函数$f_2(t)$的傅里叶变换为${\mathcal{F}}_2(\omega )$，根据公式（2）有
$$\begin{array}{rl}\mathcal{I}\mathcal{F}[{\mathcal{F}}_1(\omega )\ast {\mathcal{F}}_2(\omega )]& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }[{\int }_{-\infty }^{+\infty }{\mathcal{F}}_1(\mu ){\mathcal{F}}_2(\omega -\mu )d\mu ]e^{i\omega t}d\omega \\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\mathcal{F}}_1(\mu )e^{i\mu t}{\mathcal{F}}_2(\omega -\mu )e^{i(\omega -\mu )t}d\omega d\mu \\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{\mathcal{F}}_1(\mu )e^{i\mu t}d\mu {\int }_{-\infty }^{+\infty }{\mathcal{F}}_2(\omega -\mu )e^{i(\omega -\mu )t}d(\omega -\mu )\\ & =f_1(t)\times 2\pi \times f_2(t)\\ & =2\pi f_1(t)\times f_2(t).\end{array}$$证毕。

学得两句英语_哲理

1. A tough life needs no explanation.
2. To one who has faith, no explanation is necessary. To one without faith, no explanation is possible.

参考文献

[1] 如何通俗易懂地解释卷积？
[2] J Pan:从另一个角度看拉普拉斯变换
[3] 傅里叶变换概念及公式推导