泛函，变分与变分不等式

引言

\quad\quad 最近接触了泛函的变分的概念，回头再想变分不等式，怎么也想不明白变分不等式是如何 “变分” 的，所以重新一起看了下两者，整理在此，以便理解清晰。
\quad\quad 首先来看泛函的变分。为了解释清晰，先根据自我理解介绍下泛函的概念。

泛函

泛函定义

对于某一类函数集合 { x ( t ) } \{x(t)\} {x(t)} 中的每一个函数 $x(t)$, 在映射关系 $J$ 下均有一个确定的数与之对应，则称 $J$ 为依赖于函数 $x(t)$ 的泛函，记作$$J=J[x(.)]=J[x(t)]$$
注：泛函与函数的区别

泛函即为以函数为自变量的一种映射到实数域的映射关系。而函数则是以某一实数为自变量映射到实数域的映射关系。这里的$J[x(t)]$可理解为整条曲线 $x(t)$ 在映射关系 $J$ 下对应一个实数值。下面来解释一下泛函的自变量，如下图：

假设从[0,1]位置我们丢掷一个物体，该物体分别沿 $f(x)$, $h(x)$, $g(x)$ 三条轨道下落，同样都可降落至 [1,0]。那么我们可以将这个下落的过程称为一个泛函，三条下落的轨道曲线称为这个泛函的自变量，即泛函定义中的函数集合为 { f ( x ) , h ( x ) , g ( x ) } \{f(x),h(x),g(x)\} {f(x),h(x),g(x)}，这个物体的高度位置即为映射关系 $J$，确定的数为高度0。

泛函的变分

类似于函数中的自变量的含义，在泛函中定义域函数集合中的函数也有其自身的名称，即为宗量。

• 宗量：若函数 $x(t)$ 是映射关系 $J$ 的自变量函数，则称 $x(t)$ 为泛函 $J[x(t)]$ 的宗量函数。如上图的 $f(x)$, $h(x)$, $g(x)$ 都成为宗量函数。

同样类似于函数中两个自变量的差对应于泛函中为宗量的变分

• 宗量的变分：宗量的变分是指在同一函数类中的两个宗量函数间的差，即：$$\delta x(t)=x(t)-x^{\ast }(t).$$

类似于函数取值的差在泛函关系中用泛函增量来表示，比如上图中物体的高度在某一时刻使用不同轨道的差值。

• 泛函的增量（）
  由自变量函数 $x(t)$ 的变分 $\delta x(t)$ 引起泛函 $J[x(t)]$ 的增量 $$\Delta J=J[x(t)]-J[x^{\ast }(t)]=J[x^{\ast }(t)+\delta x(t)]-J[x^{\ast }(t)]$$ 为泛函 $J[x(t)]$ 的增量。
  即假设这里的$x(t)$ 为上图中的轨道 $f(x)$, 这里的增量即可解释为使用轨道 $f(x)$ 相较于使用轨道 $h(x)$, $g(x)$ 的物体的高度的差值。

继而，类似于函数导数的概念，在泛函中有泛函的变分的概念，即：

• 泛函的变分
  当宗量函数 $x(t)$ 有变分时，泛函 $J[x(t)]$ 的增量 $\Delta J[x(t)]$ 可表示为$$\Delta J=J[x^{\ast }(t)+\delta x(t)]-J[x(t)]=\frac{dJ}{dx}{|}_{x^{\ast }}\delta x+\frac{1}{2}\frac{d^{2}J}{d{x}^2}{|}_{x^{\ast }}(\delta x{)}^2+R,$$ 其中$\Delta J$ 的线性部分称为泛函的变分，记作 $\delta J$，即 $$\delta J=\frac{dJ}{dx}{|}_{x^{\ast }}\delta x，$$换句话说, 泛函的变分是泛函增量的线性主部。

Lemma 1: 泛函的变分 $\delta J=\frac{\partial }{\partial \alpha }J[x(t)+\alpha \delta x(t)]{|}_{\alpha =0}$

Example 1: 计算泛函 $J={\int }_0^1{x}^2(t)dt$ 的变分。
$$\begin{array}{rl}\delta J& =\frac{\partial }{\partial \alpha }J[x(t)+\alpha \delta x(t)]{|}_{\alpha =0}\\ & =\frac{\partial }{\partial \alpha }{\int }_0^1[x(t)+\alpha \delta x(t){]}^{2}dt{|}_{\alpha =0}\\ & ={\int }_0^{1}2[x(t)+\alpha \delta x(t)]\delta x(t)dt{|}_{\alpha =0}\\ & ={\int }_0^{1}2x(t)\delta x(t)dt\end{array}$$

变分不等式

首先来看一下什么叫做变分不等式。

变分不等式定义

变分不等式(variational inequality) $VI(F,X)$的正式数学定义为：

任给定义在巴纳赫空间（内积空间）$\Omega$ 的一个子集 $X$ 上的泛函 $F:X\to {\Omega }^{\ast }$, 其中 ${\Omega }^{\ast }$ 是 $\Omega$ 的对偶空间（对偶空间的解释参阅参考文献2）则$VI(F,X)$ 等价于寻找一个 $x\in X$，使得
$$⟨F(x),y-x⟩\ge 0$$对于任意的 $y\in X$成立。
在最优化方面的定义：
给定 $R^n$ 的一个子集(闭凸集) $K$以及映射 $F:K\to R^n$，变分不等式问题 $VI(K,F)$ 即为寻求一个$x^{\ast }\in K$ 使得
$$(x-x^{\ast }{)}^{T}F(x^{\ast })\ge 0$$
对任意的 $x\in K$ 成立。

变分不等式几何性解释

若可行点 $x^{\ast }$ 为变分不等式 问题 $VI(F,X)$ 的一个解，则映射 $F$ 在 $x^{\ast }$ 点处与所有可行方向 $x-x^{\ast }$, $\forall x\in K$ 之间的夹角为锐角（acute angle）

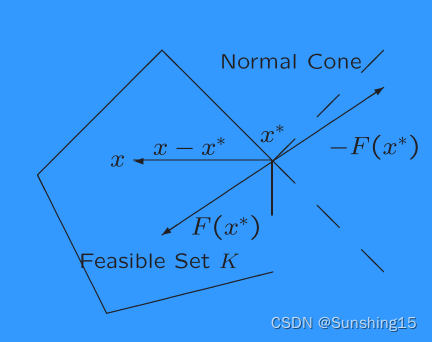
问题：还是没搞懂变分不等式的变分与泛函的变分之间的关系。变分不等式variational inequality中variational是否可解释为可变的，即可变的不等式。
自我理解：求泛函的极大值和极小值问题称为变分问题，求泛函极值的方法称为变分法。当不等式的等号成立的时候取得极值，因变分不等式与泛函的极值有关故而称为变分不等式。该命名是从变分法的定义来看的。

参考文献

1. 【优化】浅谈变分不等式与凸优化
2. 怎么形象地理解对偶空间
3. 变分不等式讲义