前两篇推文完成了对单类型事件分析的介绍,本篇将介绍多类型事件情况下的分析。
第一部分介绍多类型单事件。这种情况下,虽然事件类型有多种,但每个主体只对应一种事件结果或删失,又称竞争风险(competing risks)。
第二部分介绍多类型多事件。这种情况下,事件类型可分为存活事件和死亡事件,主体可在各种存活状态之间转移,并最终“死亡”(死亡事件发生)或删失(死亡事件未发生)。
本篇目录如下:
5 生存曲线(IV)
5.1 生存数据
5.2 竞争风险分析
5.3 手动计算生存率
6 生存曲线(V)
6.1 多状态数据
6.2 检查生存数据
6.3 计算事件发生率
预警:虽然生存曲线分了三篇推文介绍,但本篇推文篇幅仍然较长。
5 生存曲线(IV)
本部分介绍多类型单事件的生存率计算和生存曲线的绘制方法。
5.1 生存数据
每个主体只对应一种事件结果或删失,反映到数据中,就是每个主体只对应一行数据,因此这种情况下生存数据不需要主体标识变量,时间变量也只需一个(和单类型单事件类似)。但是由于可事件结果可能性有多种,生存状态变量需要使用因子类型,而不是单类型事件情况下的逻辑类型(0/1变量)。
这种情况下的一个典型生存数据示例如下:
set.seed(0822)
data <- data.frame(
id = c(1:100),
time = rpois(100, 10),
status = sample(c(0,1,2,3), 100, T)
)
data$status <- factor(data$status, labels = c("0", "A", "B", "C"))
data <- data[order(data$time, data$status, data$id),]
head(data)
## id time status
## 7 7 3 B
## 49 49 4 0
## 1 1 4 A
## 6 6 4 A
## 80 80 5 0
## 63 63 5 A
levels(data$status)
## [1] "0" "A" "B" "C"在
data中,id为主体标识变量(计算过程不需要该变量);time表示时间点;status表示生存状态变量,其中第一个水平表示删失,其他水平分别代表一种事件结果。
5.2 竞争风险分析
这种情况下的生存率计算代码和单类型单事件是一样的。如下:
library(survival)
fit <- survfit(Surv(time, status) ~ 1, data = data)
summary(fit)
## Call: survfit(formula = Surv(time, status) ~ 1, data = data)
##
## time n.risk n.event Pr((s0)) Pr(A) Pr(B) Pr(C)
## 3 100 1 0.9900 0.0000 0.0100 0.0000
## 4 99 2 0.9700 0.0200 0.0100 0.0000
## 5 96 3 0.9397 0.0402 0.0201 0.0000
## 6 92 5 0.8886 0.0709 0.0303 0.0102
## 7 85 8 0.8050 0.1336 0.0512 0.0102
## 8 74 3 0.7723 0.1553 0.0512 0.0211
## 9 66 10 0.6553 0.2021 0.0863 0.0562
## 10 54 10 0.5340 0.2628 0.1106 0.0926
## 11 40 12 0.3738 0.3296 0.1774 0.1193
## 12 26 4 0.3163 0.3439 0.2061 0.1337
## 13 20 4 0.2530 0.3914 0.2219 0.1337
## 14 16 6 0.1581 0.4388 0.2535 0.1495
## 15 10 1 0.1423 0.4546 0.2535 0.1495
## 16 9 3 0.0949 0.4546 0.2535 0.1969
## 17 5 2 0.0569 0.4546 0.2535 0.2349
## 18 3 2 0.0190 0.4926 0.2535 0.2349
## 20 1 1 0.0000 0.4926 0.2725 0.2349输出结果summary(fit),Pr(*)表示主体在该时间点处于某事件结果的概率(删失并不属于事件结果)。Pr(s(0))表示处于初始状态(initial state)的概率,即未发生任何事件的概率,因此Pr(s(0))也就是生存率。在每个时间点所有Pr(*)之和都等于1。
可以使用istate参数给初始状态命名:
library(survival)
fit.2 <- survfit(Surv(time, status) ~ 1, data = data,
istate = rep("live", 100))
summary(fit.2)
## Call: survfit(formula = Surv(time, status) ~ 1, data = data, istate = rep("live",
## 100))
##
## time n.risk n.event Pr(live) Pr(A) Pr(B) Pr(C)
## 3 100 1 0.9900 0.0000 0.0100 0.0000
## 4 99 2 0.9700 0.0200 0.0100 0.0000
## 5 96 3 0.9397 0.0402 0.0201 0.0000
## 6 92 5 0.8886 0.0709 0.0303 0.0102绘制生存曲线:
plot(fit.2, col = 1:4, lwd = 2, lty = c(1,2,2,2))
legend(15, 0.9, c("live", "A", "B", "C"),
col = 1:4, lwd = 2, lty = c(1,2,2,2), box.lty = 0)
如果只想绘制部分事件的发生概率曲线,可以对输出结果使用索引,如fit.2[,1:2]:
plot(fit.2[,1:2], col = 1:2, lwd = 2, lty = c(1,2))
legend(15, 0.9, c("live", "A"),
col = 1:2, lwd = 2, lty = c(1,2), box.lty = 0)
5.3 手动计算生存率
本节来展示这种情况下事件发生率的具体计算过程。
先统计各时间点每种事件发生的频次:
with(data, tapply(id, list(time, status), FUN = length))
## 0 A B C
## 3 NA NA 1 NA
## 4 1 2 NA NA
## 5 1 2 1 NA
## 6 2 3 1 1
## 7 3 6 2 NA
## 8 5 2 NA 1
## 9 2 4 3 3
## 10 4 5 2 3
## 11 2 5 5 2
## 12 2 1 2 1
## 13 NA 3 1 NA
## 14 NA 3 2 1
## 15 NA 1 NA NA
## 16 1 NA NA 3
## 17 NA NA NA 2
## 18 NA 2 NA NA
## 20 NA NA 1 NA定义向量:
其中Pr(*)表示主体在时处于某事件结果的概率。
使用转移矩阵表示从状态转移到状态的概率,它的每行元素之和始终等于1。在单事件情况下,只有从初始状态(存活状态)转移到其他事件状态这种可能。
在时,P(0) = c(1,0,0,0),转移矩阵为对角阵:
P0 <- matrix(c(1,0,0,0), nrow = 1)
TM <- diag(4)
TM
## [,1] [,2] [,3] [,4]
## [1,] 1 0 0 0
## [2,] 0 1 0 0
## [3,] 0 0 1 0
## [4,] 0 0 0 1在时,风险集n.risk为100,只有事件B发生一次,因此从初始状态转移到其他状态的概率也就是TM的第一行元素为c(99, 0, 1, 0)/100。
TM[1,] <- c(99, 0, 1, 0)/100
P1 <- P0 %*% TM
P1
## [,1] [,2] [,3] [,4]
## [1,] 0.99 0 0.01 0在时,风险集n.risk为99,事件A发生两次(删失也发生一次,但不影响计算生存率和事件发生率),因此TM第一行元素为c(97, 2, 0, 0)/99。
TM[1,] <- c(97, 2, 0, 0)/99
P2 <- P1 %*% TM
P2
## [,1] [,2] [,3] [,4]
## [1,] 0.97 0.02 0.01 0在时,风险集n.risk为96,事件A发生两次,事件B发生一次,因此TM第一行元素为c(93, 2, 1, 0)/96。
TM[1,] <- c(93, 2, 1, 0)/96
P3 <- P2 %*% TM
P3
## [,1] [,2] [,3] [,4]
## [1,] 0.9396875 0.04020833 0.02010417 06 生存曲线(V)
本部分介绍多类型多事件的生存率计算和生存曲线的绘制方法。
6.1 多状态数据
在多类型多事件的情况下,事件类型可分为存活事件和死亡事件。死亡事件是研究所关注的事件,而存活事件一般是影响死亡事件的因素;主体可在各种存活状态之间转移,并最终“死亡”(死亡事件发生)或删失(死亡事件未发生)。
myeloid是多状态数据(multi-state data)的一个示例。由于我们不需要考虑事件的实际含义,这里使用A、B、C分别代表三种存活事件。
data0 <- myeloid[, -3]
names(data0)[5:7] <- c("A", "B", "C")
head(data0)
## id trt futime death A B C
## 1 1 B 235 1 NA 44 113
## 2 2 A 286 1 200 NA NA
## 3 3 A 1983 0 NA 38 NA
## 4 4 B 2137 0 245 25 NA
## 5 5 B 326 1 112 56 200
## 6 6 B 2041 0 102 NA NA
id表示主体标识,trt为协变量,futime表示最后受访时间,death表示最后受访事件时的状态变量,其中1表示死亡,0表示删失,A、B、C分别表示处于相应状态事件的时间点,其中NA表示主体未处于过该状态。
和单类型多事件一样(见推文《生存曲线(中)》),我们需要先进行数据转换以形成时间区间。survival工具包的tmerge()函数可以帮助我们更方便地完成这一过程。代码如下:
data2 <- tmerge(data1 = data0[,1:2],
data2 = data0, id = id,
death = event(futime, death),
A = event(A), B = event(B), C = event(C))
head(data2)
## id trt tstart tstop death A B C
## 1 1 B 0 44 0 0 1 0
## 2 1 B 44 113 0 0 0 1
## 3 1 B 113 235 1 0 0 0
## 4 2 A 0 200 0 1 0 0
## 5 2 A 200 286 1 0 0 0
## 6 3 A 0 38 0 0 1 0
data1表示生存数据中的主体信息变量(标识变量、协变量等);
data2表示完整生存数据;
id表示标识变量名;新生成的事件变量为逻辑类型,使用辅助函数
event()引用原数据相应变量得到;其中死亡事件变量需要引用最后受访时间变量(futime)和死亡状态变量(death),存活事件变量仅引用对应事件变量(A、B、C);新生成的
tstart和tstop变量表示时间区间的起始和终止点。
生存数据不允许时间区间长度为0,即同一主体不能在同一时间点发生多种事件结果。我们可以使用下面代码进行检查:
l = which(with(data2, death + A + B + C) > 1)
data2[l,]
## id trt tstart tstop death A B C
## 1119 428 A 0 24 0 1 1 0可以看到,id为428的主体在t = 24时发生了A、B两种事件结果。对此,我们可以将事件A发生的时间稍微往前调一下,然后重新进行数据转换:
data0[data0$id == 428, "A"] <- data0[data0$id == 428, "A"] - 0.01
data2 <- tmerge(data1 = data0[,1:2],
data2 = data0, id = id,
death = event(futime, death),
A = event(A), B = event(B), C = event(C),
tA = tdc(A), tB = tdc(B), tC = tdc(C))
which(with(data2, death + A + B + C) > 1)
## integer(0)在上面代码中,我们还使用辅助函数tdc()生成了逻辑变量tA、tB、tC。
以tA为例,在主体发生事件A的时间区间及其之前的时间区间均记为0,之后的时间区间均记为1。示例如下:
data2[data2$id == 1, c(1,3:11)]
## id tstart tstop death A B C tA tB tC
## 1 1 0 44 0 0 1 0 0 0 0
## 2 1 44 113 0 0 0 1 0 1 0
## 3 1 113 235 1 0 0 0 0 1 1最后根据事件变量生成生存状态变量:
library(tidyverse)
data2 <- data2 %>%
mutate(status = case_when(
death == 1 ~ "death",
A == 1 ~ "A",
B == 1 ~ "B",
C == 1 ~ "C",
id > 1 ~ "none"),
status = factor(status, levels = c("none", LETTERS[1:3], "death"))) %>%
select(-LETTERS[1:3])
levels(data2$status)
## [1] "none" "A" "B" "C" "death"
table(data2$status)
## none A B C death
## 325 364 454 226 3206.2 检查生存数据
可以使用survcheck()函数来检查生存数据中事件及其转移的情况:
survcheck(Surv(tstart, tstop, status) ~1,
data = data2, id = id)结果解读如下:
## Unique identifiers Observations Transitions
## 646 1689 1364上表表明数据中共有646个主体(样本),1689个时间区间,发生1364次事件之间的转移。
## Transitions table:
## to
## from A B C death (censored)
## (s0) 107 442 13 55 29
## A 0 12 45 149 157
## B 158 0 168 17 111
## C 99 0 0 99 28
## death 0 0 0 0 0上表展示了事件转移的具体分布情况。
(s0)表示初始状态。如从A转移到B为12次,从B转移到A有158次;死亡作为终止性事件,转移到其他事件的次数均为0。
## Number of subjects with 0, 1, ... transitions to each state:
## count
## state 0 1 2 3 4
## A 282 364 0 0 0
## B 192 454 0 0 0
## C 420 226 0 0 0
## death 326 320 0 0 0
## (any) 29 201 174 153 89上表为事件发生次数对应的主体数量统计表。如事件A发生零次的有282人,发生一次的364人,发生两次及以上的为0人;任何事件都没发生过的有29人(从初始状态直接删失),仅发生一次事件的有201人。
6.3 计算事件发生率
6.3.1 情况一
考虑所有事件状态,并允许各种转移情况的存在。函数计算的不再是生存率,而是各种事件状态的发生率(包括死亡率)。
fit.3 <- survfit(Surv(tstart, tstop, status) ~ 1,
data = data2, id = id)
plot(fit.3, col = c(2:4,1), lwd = 2, lty = c(2,2,2,1))
legend(230, 0.65, c("A", "B", "C", "death"),
col = c(2:4,1), lwd = 2, lty = c(2,2,2,1),
box.lty = 0)
6.3.2 情况二
只考虑事件A和死亡事件两种情况,这时就需要把发生其他事件的时间区间的状态变量设定为删失(none)。
data2 <- data2 %>%
mutate(temp= if_else(status %in% c("A", "death"), status, factor("none")),
statusA = factor(temp, levels = c("none", "A", "death")))
fit.4 <- survfit(Surv(tstart, tstop, statusA) ~ 1, data = data2,
id = id)
plot(fit.4, col = 2:1, lwd = 2, lty = 2:1)
legend(1500, 0.2, c("A", "death"),
col = 2:1, lwd = 2, lty = 2:1, box.lty = 0)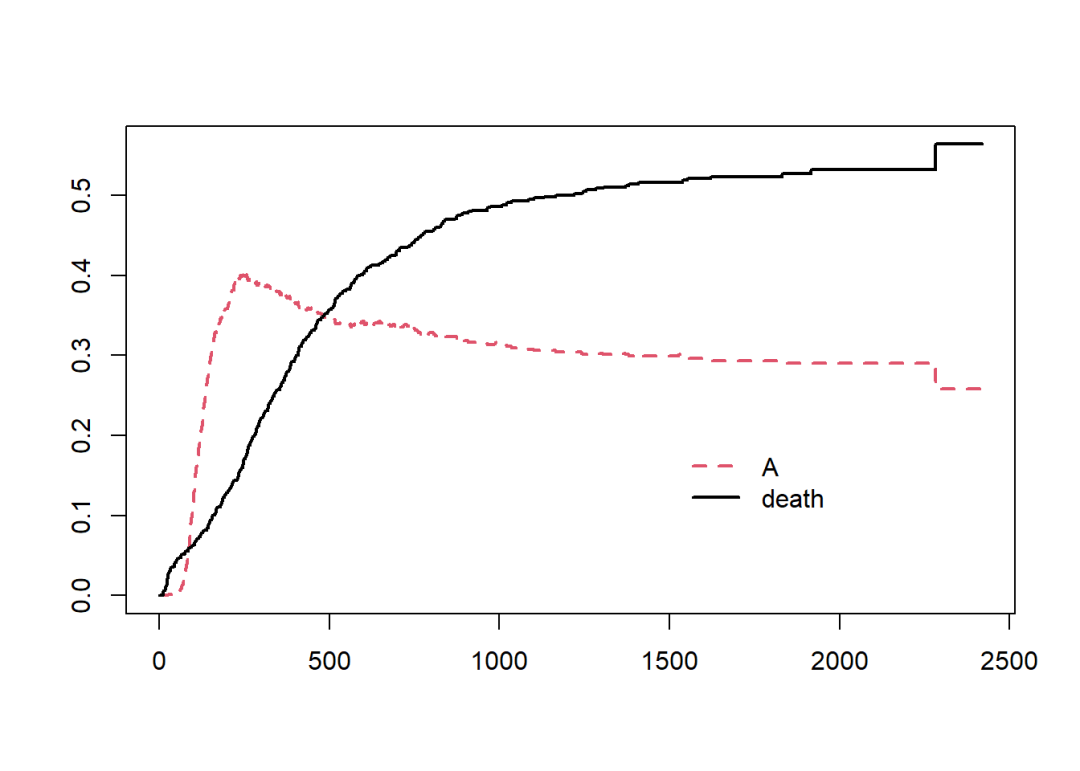
6.3.3 情况三
分析事件B和死亡事件之间的竞争风险,可以理解成事件比竞争事件更早发生的概率。这种情况其实就转换成了多类型单事件的分析。此时,新的状态变量statusB在每个时间区间有如下三种可能:
发生了事件B;
死亡并且之前未发生事件B;
删失。
这种情况与情况二的区别在于,它不允许在死亡之前发生事件B(此种情况需要设定为删失)。这时就可以利用此前定义的变量tB了,凡是tB = 1的时间区间说明再次之前主体已发生了事件B,因此状态需设定为删失。
data2 <- data2 %>%
mutate(temp = "none",
temp = if_else(status == "death" & tB == 0, "death", temp),
temp = if_else(status == "B", "B", temp),
statusB = factor(temp, levels = c("none", "B", "death")))
fit.5 <- survfit(Surv(tstart, tstop, statusB) ~ 1, data = data2,
id = id)
plot(fit.5, col = 2:1, lwd = 2, lty = 2:1)
legend(1500, 0.5, c("B", "death"),
col = 2:1, lwd = 2, lty = 2:1, box.lty = 0)
6.3.4 情况四
分析事件A和B之间的竞争风险,这是对情况三的一般化。凡是tA = 1或tB = 1的时间区间的状态都需设定为删失。
data2 <- data2 %>%
mutate(temp = "none",
temp = if_else(status == "A" & tB == 0, "A", temp),
temp = if_else(status == "B" & tA == 0, "B", temp),
statusAB = factor(temp, levels = c("none", "A", "B")))
fit.6 <- survfit(Surv(tstart, tstop, statusAB) ~ 1, data = data2,
id = id)
plot(fit.6, col = 2:3, lwd = 2, lty = 2)
legend(1500, 0.5, c("A", "B"),
col = 2:3, lwd = 2, lty = 2, box.lty = 0)
6.3.5 情况五
分析是否在死亡前发生事件C的影响。这种情况就把死亡状态分成了两类:死亡并且未发生事件C、死亡并且之前发生了事件C。
data2 <- data2 %>%
mutate(temp = "none",
temp = if_else(status == "death" & tC == 0, "without C", temp),
temp = if_else(status == "death" & tC == 1, "after C", temp),
statusC = factor(temp, levels = c("none", "without C", "after C")))
fit.7 <- survfit(Surv(tstart, tstop, statusC) ~ 1, data = data2,
id = id)
plot(fit.7, col = 2:3, lwd = 2, lty = 2)
legend(1500, 0.1, c("without C", "after C"),
col = 2:3, lwd = 2, lty = 2, box.lty = 0)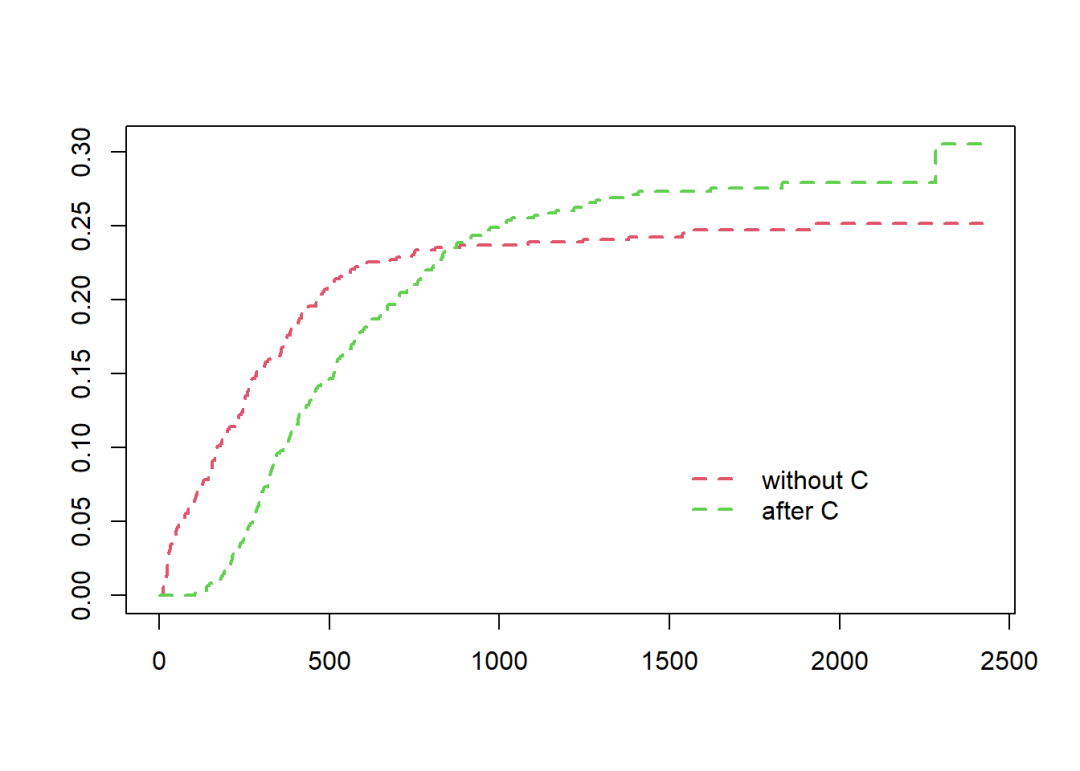








 本文详细介绍了在多类型事件背景下如何进行生存率计算和生存曲线绘制。首先,对于多类型单事件,即使每个主体只对应一种事件结果或删失,也需用因子类型的生存状态变量。通过`survival`包的`survfit`函数,可以计算并展示不同事件的概率。接着,对于多类型多事件,数据需转换为多状态数据形式,允许主体在不同存活状态间转移。使用`tmerge`函数处理数据,然后通过`survfit`计算不同事件发生率,绘制生存曲线。文章提供了具体代码和实例,涵盖了从数据预处理到结果分析的全过程。
本文详细介绍了在多类型事件背景下如何进行生存率计算和生存曲线绘制。首先,对于多类型单事件,即使每个主体只对应一种事件结果或删失,也需用因子类型的生存状态变量。通过`survival`包的`survfit`函数,可以计算并展示不同事件的概率。接着,对于多类型多事件,数据需转换为多状态数据形式,允许主体在不同存活状态间转移。使用`tmerge`函数处理数据,然后通过`survfit`计算不同事件发生率,绘制生存曲线。文章提供了具体代码和实例,涵盖了从数据预处理到结果分析的全过程。
















 396
396

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








