【随机过程01】高斯过程

参考视频：工科随机过程 中国科学院大学 带目录完整版 授课教师张颢 清华大学 21集全 应用随机过程 随机过程应用 适用于信息类 金融类同学观看（P6-8）

随机过程教学内容大致可以分成两类：

1. 随机过程一般性的描述：即并不着眼于某一类特殊的过程，而是着眼于研究随机过程一般意义上的方法。随机过程是研究随机变量之间的相互关联：线性、马尔可夫、鞅。

   线性关联研究的主要工具是相关函数，相关函数可以从时域频域两个角度认识，在时域上是相关函数，在频域上是功率谱密度。相关函数考察的是：随机过程在两个时刻的取值得到的随机变量之间的相互关联，即这两个随机变量之间在多大程度上可以被相互地线性表出。由这个概念，我们还引出了宽平稳，非宽平稳。

2. 涉及到某类具体的随机过程

   高斯过程和泊松过程在整个随机过程中占据着核心地位。这两个随机过程是我们迄今为止，认识得最清楚的最深刻两类随机过程。他们的理论最为自洽和优美，应用最为广泛。

高斯在密度当中有表达两个随机变量关联的因素存在，这个因素恰好是相关运算。这表明高斯分布，特别是多元高斯分布，他与相关线性表出等等知识是有着内在联系的。

而高斯过程就是用N维高斯分布来进行定义的。所以我们把N维高斯分布作为学习高斯过程的核心内容。
$$f_X(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}(det\Sigma {)}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$
从知识体系的延伸来说，当我们进入一个新的知识领域的时候，我们会不可避免地问自己一个问题，就是研究这个问题的motivation是什么？——高斯分布有何奇特之处？以下将从三个不同的方面来说明：为什么高斯分布生来就是做概率统计的老大。

1. Motivation

1.1 中心极限定理

再说中心极限定理之前，先说一说大数定律：

大数定律：

$$\frac{X_1+X_2+\cdot \cdot \cdot +X_N}{N}=E(X_1)X_i\sim i.i.d$$

这个极限起到的作用就是把$X_i$的随机性通过叠加（想象正负相交有这么一种感觉）把随机起伏的效应涨落全部都通过平均消除掉，把确定性的部分能够浮出水面。而这确定性的部分恰好就是期望。

中心极限定理：

$$\frac{X_1+X_2+\cdot \cdot \cdot +X_N}{\sqrt{N}}\sim N(0,1)E(X_i)=0,Var(X_i)=1$$

中心极限并没有把它的随机性全部消除掉，而是留下了一些公共部分，即这些随机变量都拥有的、非常能够反应随机本质的部分。这是一个随机性规律非常确定的随机变量：就是高斯。

由此可见，高斯在随机变量之间起着一个核心的作用，因为各个随机变量之间都多多少少含有高斯的成分，当你约束了之后，高斯的成分就凸显出来了。

证明：特征函数

$${\Phi }_X(w)={\int }_R{f}_X(x)exp(jwx)dx=F^{-1}(f_X(x))$$

特征函数是概率密度的傅里叶反变换，$指数里面-jwx$是傅里叶变换，特征函数是作为随机变量的特征性质出现的，每一个随机变量都有自己的概率密度，而特征函数与概率密度之间是傅里叶变换对，1:1的。

特征函数最重要的性质是可加性：
$$\begin{gathered} Y=X_1+\cdot \cdot \cdot +X_n{X}_i\sim independent \\ {\Phi }_Y(w)=\prod _{k=1}^n{\Phi }_{X_K}(w) \end{gathered}$$
随机变量的和，原本是会让随机性增强（方差变大），让复杂度增加。但是有了特征函数，处理起来就得心应手。

我们研究概率论，一半以上的工作是在做积分，因为我们总得求和，概率最重要的特性就在于他是可加的，即概率最重要的理念，就在于他认为不确定度是可以加在一起的，我们算的所有的概率理论上都是在做加法，即积分。

中心极限定理告诉我们：大量微小的随机因素叠加在一块的时候，呈现的整体的统计效应是高斯。因此，高斯无处不在。噪声为什么经常假设为高斯？电子设备的热噪声很多是来自“霰弹效应”，阴极射线板之间有很多电子挣脱束缚，在电场的作用下运动，从一个射线板到达另外一个射线板，会有一个冲击。这个冲击作为一个电子而言效应非常微小。但是有大量这样的冲击，叠加在一起，总体的效应就很可观。你很难仔细地去研究这个冲击本身特性是什么，不过已经不必要了，原因在于大量的冲击叠加在一起，总体的效应一定是高斯。

1.2 分子运动

1.3 最大熵原理

高斯是最随机的随机变量，因为它又最大熵，随机性最强，最具典型意义。最值得研究，最好研究，最有解析解。

以上我们从不同的角度认识了我们为什么要学高斯，motivation非常的重要。为什么中国人民志愿军能够在那么艰苦的条件下，能够在武器存在代差的条件下可以和当时世界上最强的军队打成平手，就是因为我们解决了为什么要打仗的问题，我们的士气，我们的意志力是绝对超过美军的。这绝对是当时世界上最强的轻武兵，没有之一，就因为我们解决了为什么打仗的问题。

---

现在我们回到多元高斯分布：
$$f_X(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}(det\Sigma {)}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$
首先我们来检查一下这的确是一个概率密度。我们在检查这样一个显然是事实的过程中，我们可以体会在多元高斯的学习过程中，我们需要去经理哪些困难，以及我们需要去掌握的哪些手段。

我们再来看特征函数从一维延伸到多维：

1. 多元高斯的线性不变性：

2. 边缘分布仍然是高斯的：

直观的想象：多元高斯已经是一个钟型了。从联合分布求边缘分布不是在切，而是在挤。钟型挤成一片还是钟型。但是反过来就不一定了。挤出来是个钟型，还原回去还真不一定就是钟型。

2. 联合高斯

对于一组随机变量，我们是否有办法能够判断它的联合高斯性？有没有一种办法，它不仅仅是看每一个分量，他的看法应当是更加的宏观，且更加的有控制力。利用这样的方法。我们能够去判断联合高斯性：

2.1 判断多元高斯的充要条件

$$X\in R^{n}X\sim N\iff \forall \alpha \in R^n{\alpha }^{T}X\sim N$$

这是我们联合高斯的特征性质。X的分量之间的任意的线性组合都是高斯的。

2.2 相关性和独立性

不相关不等于独立，这说明两个随机变量的关系已经有点远了，在两阶上已经是没有关系了。但是它并不是独立的，因为他们可能存在更高阶的关联。用二阶矩没有办法描绘的关联。回到高斯，我们不禁会产生这样的疑问，既然高斯是完全由一阶矩和二阶矩可以确定下来，那么两个高斯的随机变量不相关是否能推得独立呢？不能，得要联合高斯。

对于多元高斯，不相关性和独立性存在这等价关系。
$$\begin{gathered} X=(X_1,\cdot \cdot \cdot ,X_n)\sim N \\ E(X_i{X}_j)=E(X_i)E(X_j),\forall i,j\Rightarrow (X_i,\cdot \cdot \cdot ,X_n)IsMutuallyIndependent \end{gathered}$$
我们也不是完全不能由边缘推出联合高斯。**条件就是分量之间相互独立。**即独立的情况下，边缘是高斯，联合也是高斯。
$$\begin{gathered} (X_i,\cdot \cdot \cdot ,X_n)IsMutuallyIndependent \\ {X}_k\sim N,(k=1,2,\cdot \cdot \cdot ,n)\Rightarrow X=(X_1,\cdot \cdot \cdot ,X_n)\sim N \end{gathered}$$

2.3 Cochran Theorem

如果样本是高斯分布，那么样本均值和样本方差就是独立的

3. 条件期望

$$E(X_1|X_2)={\mu }_1+\frac{{\sigma }_{12}}{{\sigma }_{22}}(X_2-{\mu }_2)$$

条件期望意味着我这时知道了关于X2的信息，这一部分知识，换句话讲，我对于X1而言不是一无所知，至少X2里头和X1相关的这部分信息已经被我把握住了。所以在这种情况下，我对于X1的认识势必要进行一下更改，我的更改要基于我所知道的知识。X1 X2相关性越强，做出的调整就越大。
$${\Sigma }_{1|2}={\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}$$
方差一定是变小的，因为我们获得了X2关于X1的部分知识，而熵一定是减小的。

而我对于X1和X2的认识是从相关的角度，只在线性的程度上进行认识，但是在这个程度上认识就够了。因为这是高斯，这就是最优，我这个调整是能够做出来的最优的调整。因为他是条件期望。条件期望是均方意义下的最优。

3.1 条件期望是均方意义下的最优

对于高斯分布，它的条件期望是线性的，所以最优线性估计和最有估计是相等的。

4. 非线性

我们希望研究非线性操作下，高斯具有什么样的性态。

4.1 多项式

1. 一维高斯的高阶矩：

$E(X^n)=-\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\infty }^{+\infty }{x}^n{e}^{-\frac{x^2}{2{\sigma }^2}}$

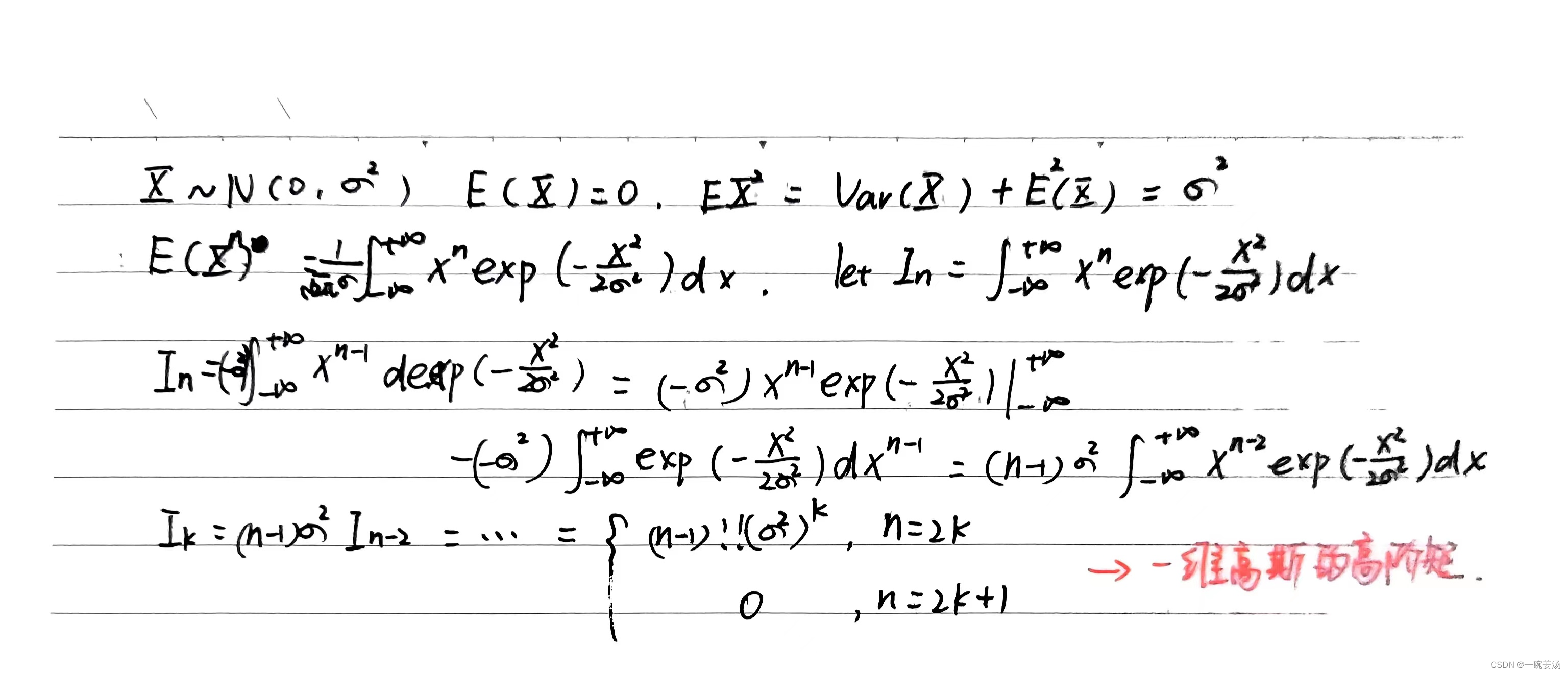
可以看到奇数阶矩留不下来，如果高斯的均值是零。偶数阶矩不管多高的阶数都可以表示成二阶矩。

2. 平方器->卡方分布

$Y(t)=X^2(t)$

3. 平方器相关函数

高斯过程，平方器输出的相关涉及到的相关是自身的四阶矩的计算。
$$R_Y(t,s)=E(X^2(t)X^2(s))=R_X^2(0)+R_X^2(t-s)+R_X^2(t-s)=R_X^2(0)+2R_X^2(t-s)$$
搞清楚平方器后，多项式就对我们没有本质性的难度了。剩下的只是一些繁琐的计算。

4.2 分段线性

1. 硬限幅器->相关函数

$$\begin{gathered} P(X(t)X(s)\ge 0)=\frac{1}{2}+\frac{1}{\pi }si{n}^{-1}(\frac{R_X(t-s)}{R_X(0)}) \\ P(X(t)X(s)<0)=\frac{1}{2}-\frac{1}{\pi }si{n}^{-1}(\frac{R_X(t-s)}{R_X(0)})\text{\hspace{1em}(13)} \end{gathered}$$
公式（13）揭示了：随着$\rho$慢慢由0向非零转变，第一象限的概率是如何变化的。

2. 反正弦定理

最终得出相关函数，有个名字叫反正弦定理（Arcsin Law）：
$$R_Y(t,s)=\frac{2}{\pi }si{n}^{-1}(\frac{R_X(t-s)}{R_X(0)})$$
这个结论得出的过程其实不难，因为都是恒等式，恒等式就意味着你要过河的话，那个石头都给你摆好了，只不过因为天有些黑，所以你看不太见，并不等于那儿没有，如果你眼力好，或者打上一个火把，你就蹭蹭蹭过去了，真正难的是前边根本没石头，往前一迈就掉进去了，你得自己弄一块石头往前一拽，走一步，再拿块石头往前一拽，再走一步。这才是难的。

3. Price 定理

$$\begin{gathered} (X_1,X_2)\sim N(0,0,{\sigma }_1^2,{\sigma }_2^2,\rho ) \\ E(g(X_1,X_2))\Rightarrow \frac{\partial E(g(X_1{X}_2))}{\partial \rho }=({\sigma }_1{\sigma }_2)E(\frac{\partial g^2(X_1{X}_2)}{\partial X_1\partial X_2}) \end{gathered}$$

price定理三部曲：

1. 指示函数

2. ReLU函数

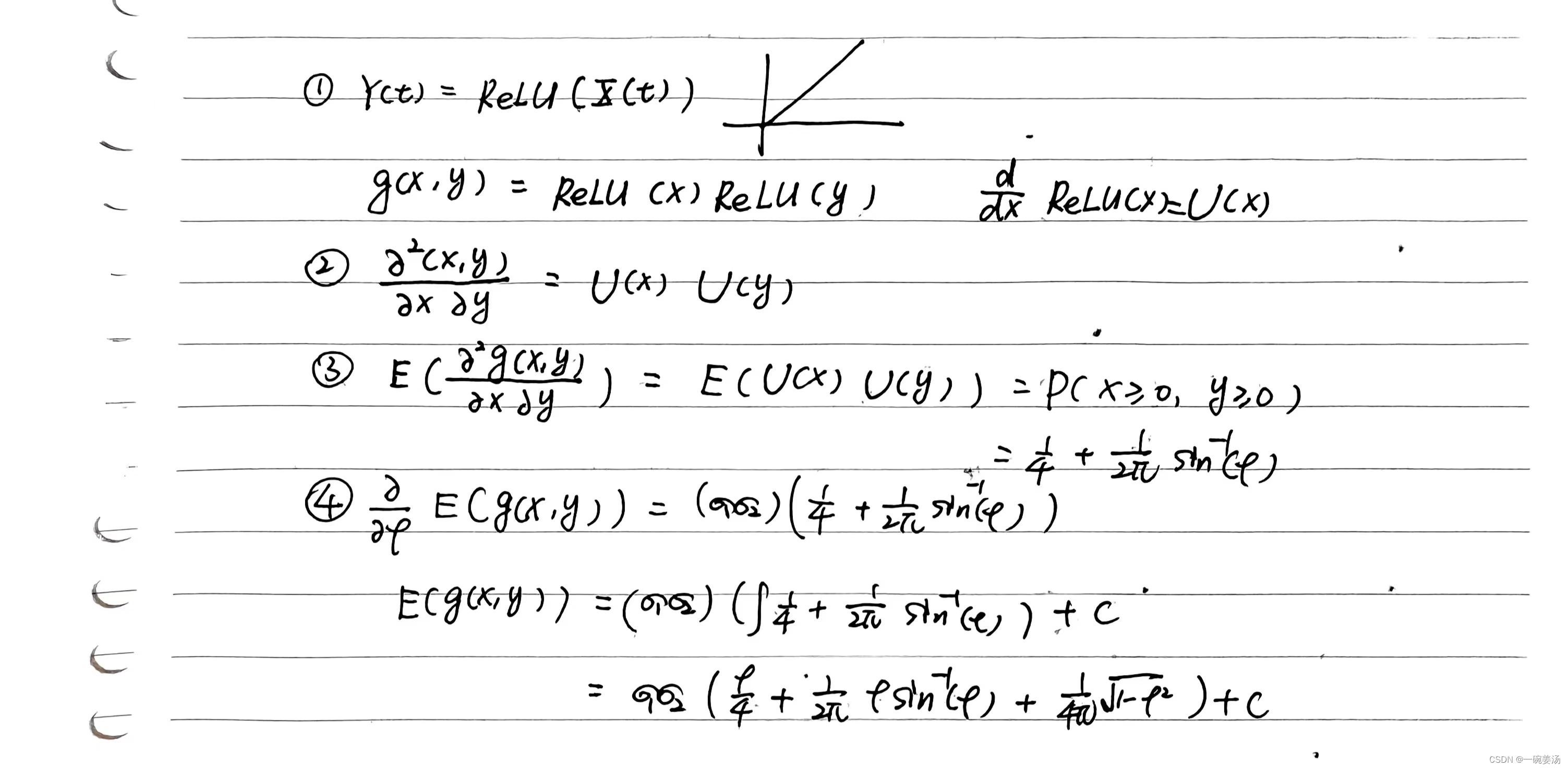
3. 平方器

4.3 指数函数

1. 对数正态：特征函数

4.4 三角函数

积分是积不出来的，Price定理看上去也有些艰险：$\frac{d^2}{d{\rho }^2}z(\rho )=z(\rho )$

但是注意到：因为三角函数和指数函数是一回事，所以特征函数又可以拥用上去了，我们有欧拉公式：
$$cos\theta =\frac{1}{2}(exp(j\theta )+exp(-j\theta ))$$

4.5 总结

处理非线性问题，我们一共有三招：

1.积分（一般不要用）

2.Price定理（一般情况下很好用）

3.特征函数（指数函数的情况下特别好用）

三角函数和指数函数是一个意思。我们中学给大家打下的烙印不太对，把这两者生生地割裂开，这是因为我们没有强调复平面的核心作用，所以应当先教复数，建立起平面、矢量的概念，把二维平面的矢量与复数能够建立起联系，随后诸如什么三角变换，旋转，平移等等一系列问题都迎刃而解了，你想想旋转不就是乘上一个复因子嘛，到线性代数就是乘上一个矩阵了，事实上，矩阵$\left(\begin{array}{cc}C& -S\\ S& C\end{array}\right)\sim C+jS$ 是同构。$\left(\begin{array}{cc}{C}^{(\theta )}& -S^{(\theta )}\\ S^{(\theta )}& C^{(\theta )}\end{array}\right)\sim e^{j\theta }$

从历史上来看，复数的出现和直角坐标系的出现是同时的。笛卡尔创立直角坐标系，几乎同一年莱布尼兹在考虑-1的开方。

非线性这一部分知识研究的热潮是在五六十年代，当时的电子信息系统，特别是对电路的研究很盛行，电路的核心因素是算噪声特性。通常都把噪声假设为高斯，所以就意味着高斯通过非线后的性态是我们必须要面对的课题。输入是个白噪声，输出是什么谱，要随着噪声在电路里头一级一级的变化，做很多的操作，让这个噪声的性质在他的把控之中。

非线性也就高斯背景下能玩一玩，别的都是瞎掰。

现在的所谓智能主要来自于非线性，卷积层是用一个个pattern去卷这个输入，为什么现在越来越流行用小pattern了，其实刚一开始5x5、7x7的很多人用，为什么现在都落到3x3了？因为用小pattern，这个维度下降的不是那么快，而我们可以有更多的非线性可以介入进来，为什么人们喜欢用更深的网络，其实原因也在于我们要有更多的非线性要接入进来，线性能够产生的故事和产生的现象，太过有限了。只有更多地非线性介入进来之后，我们才能有一个更好地智能的基础。