NSGAII算法和MOEAD算法是多目标优化领域的两大经典算法。相较于NSGAII算法,MOEAD算法更难理解,主要难点在不能很好理解三种分解方法(尤其是后两种)。本文旨在通过对等高线的分析来帮助理解三种分解策略。为便于理解,本文的目标函数数量均为2。
为方便分析,本文采用改进的切比雪夫分解法。(其实道理类似)
改进的切比雪夫(Modified Tchebycheff)分解法的数学表达式为:
$$
\begin{align*}
min \;\; g^{mtch}(x | \lambda,z^{*}) = \max_{1\le i\le m} \left \{ \frac{f_{i}(x)-z^{*}_{i}}{\lambda_{i}} \right \}
\tag{1}
\end{align*}
$$
不妨令\( f_{i} = f_{i}-z^{*}_{i} \)(这边的式子不太严谨,其实就是把目标函数空间平移一下,意思懂就行)。那么MTCH分解法的数学表达式就变成了:
$$
\begin{align*}
min \;\; g^{mtch}(x | \lambda,z^{*}) = \max_{1\le i\le m} \left \{ \frac{f_{i}(x)}{\lambda_{i}} \right \}
=\max \left \{ \frac{f_{1}(x)}{\lambda_{1}} ,\frac{f_{2}(x)}{\lambda_{2}} \right\}
\tag{2}
\end{align*}
$$
此时就有两种情况:1)向量\( \overrightarrow{f} \)在向量\( \overrightarrow{\lambda} \)下方;2)向量\( \overrightarrow{f} \)在向量\( \overrightarrow{\lambda} \)上方。
1)向量\( \overrightarrow{f} \)在向量\( \overrightarrow{\lambda} \)下方
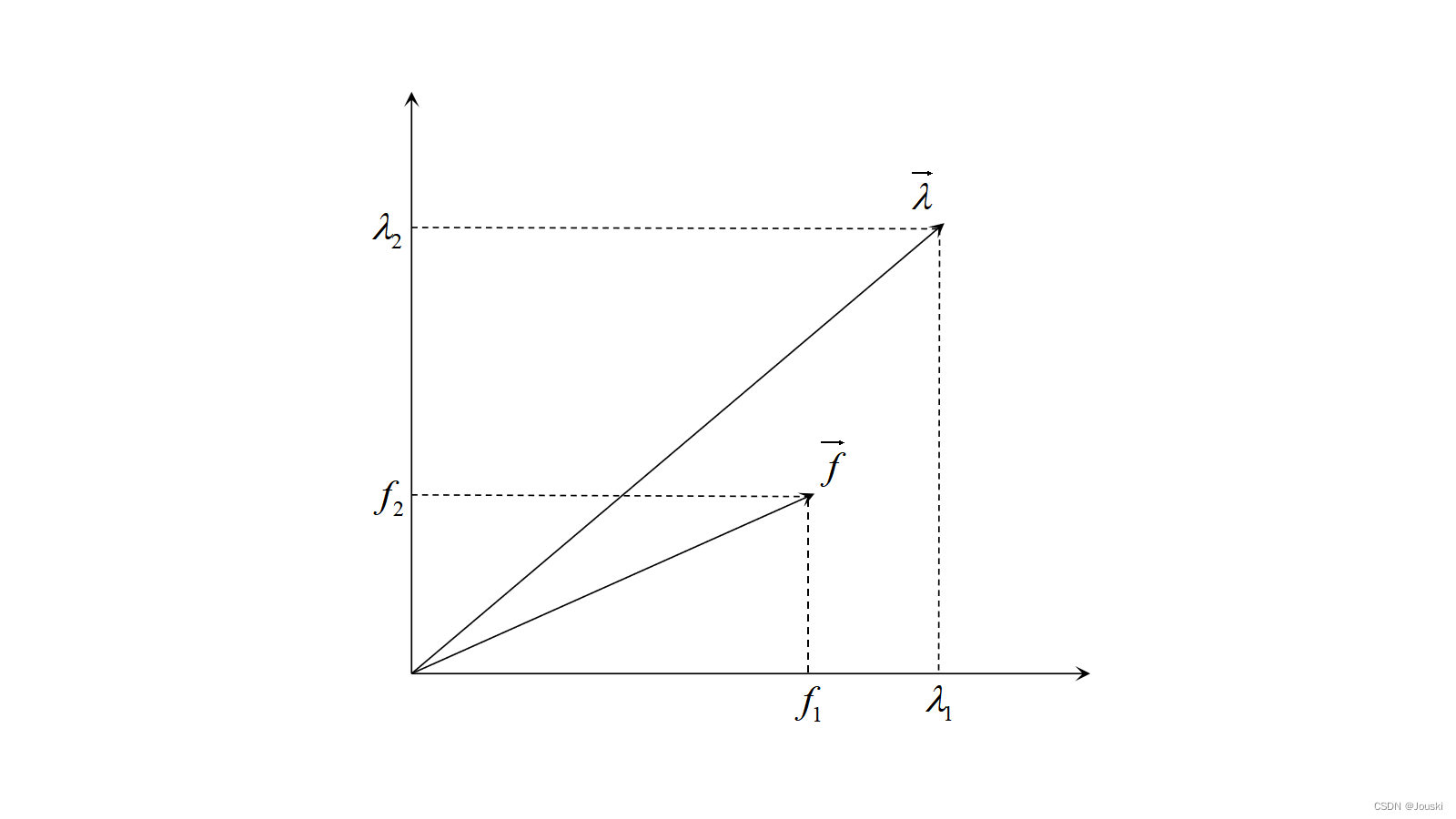
图1
由图1可以看出,向量\( \overrightarrow{\lambda} \)方向的直线斜率大于向量\( \overrightarrow{f} \)方向的直线斜率,所以有:
$$
\begin{align*}
\frac{\lambda_{2}}{\lambda_{1}} > \frac{f_{2}}{f_{1}}
\tag{4}
\end{align*}
$$
简单变换一下,可以得出:
$$
\begin{align*}
\frac{f_{1}}{\lambda_{1}} > \frac{f_{2}}{\lambda_{2}} \Rightarrow
max \left \{ \frac{f_{1}}{\lambda_{1}},\frac{f_{2}}{\lambda_{2}} \right \}
=\frac{f_{1}}{\lambda_{1}}
\tag{5}
\end{align*}
$$
将(5)代入(2),可以得到
$$
\begin{align*}
g^{mtch}(x | \lambda,z^{*}) = \frac{f_{1}}{\lambda_{1}}
\tag{6}
\end{align*}
$$
由于\( \lambda_{1} \)是定值,所以可以认为\( g^{mtch}(x | \lambda,z^{*}) \)仅取决于\( f_{1} \)。如图2所示,显然线段\( l \)上的点与向量\( \overrightarrow{\lambda} \)的\( g^{mtch} \)值相同,因此线段\( l \)是一条等高线。

图2
2)向量\( \overrightarrow{f} \)在向量\( \overrightarrow{\lambda} \)上方
 图3
图3
由图1可以看出,向量\( \overrightarrow{f} \)方向的直线斜率大于向量\( \overrightarrow{\lambda} \)方向的直线斜率,所以有:
$$
\begin{align*}
\frac{f_{2}}{f_{1}} > \frac{\lambda_{2}}{\lambda_{1}}
\tag{7}
\end{align*}
$$
简单变换一下,可以得出:
$$
\begin{align*}
\frac{f_{2}}{\lambda_{2}} > \frac{f_{1}}{\lambda_{1}} \Rightarrow
max \left \{ \frac{f_{1}}{\lambda_{1}},\frac{f_{2}}{\lambda_{2}} \right \}
=\frac{f_{2}}{\lambda_{2}}
\tag{8}
\end{align*}
$$
将(8)代入(2),可以得到
$$
\begin{align*}
g^{mtch}(x | \lambda,z^{*}) = \frac{f_{2}}{\lambda_{2}}
\tag{9}
\end{align*}
$$
由于\( \lambda_{2} \)是定值,所以可以认为\( g^{mtch}(x | \lambda,z^{*}) \)仅取决于\( f_{2} \)。如图4所示,显然线段\( l \)上的点与向量\( \overrightarrow{\lambda} \)的\( g^{mtch} \)值相同,因此线段\( l \)是一条等高线。

图4
对于某个向量\( \overrightarrow{\lambda} \),个体在2维目标函数空间的分布有如下4种情况。
1)两个体都在向量\( \overrightarrow{\lambda} \)上方,如图5中的\( x_{1} \)和\( x_{2} \)。由于\( f_{2}(x_{2}) < f_{2}(x_{1}) \),所以\( g^{mtch}(x_{2}|\lambda,z^{*}) = \frac{f_{2}(x_{2})}{\lambda_{2}} < g^{mtch}(x_{1}|\lambda,z^{*}) = \frac{f_{2}(x_{1})}{\lambda_{2}} \),因此可以认为个体\( x_{2} \)优于个体\( x_{1} \)。
2)两个体都在向量\( \overrightarrow{\lambda} \)下方,如图5中的\( x_{3} \)和\( x_{4} \)。同理可以得出个体\( x_{3} \)优于个体\( x_{4} \)。
3)两个体都在向量\( \overrightarrow{\lambda} \)上,如图5中的\( x_{5} \)和\( x_{6} \)。此时对于\( x_{5} \)有\( g^{mtch}(x_{5}|\lambda,z^{*}) = \frac{f_{1}(x_{5})}{\lambda_{1}} = \frac{f_{2}(x_{5})}{\lambda_{2}} \);对于\( x_{6} \)有\( g^{mtch}(x_{6}|\lambda,z^{*}) = \frac{f_{1}(x_{6})}{\lambda_{1}} = \frac{f_{2}(x_{6})}{\lambda_{2}} \)。而\( \frac{f_{1}(x_{5})}{\lambda_{1}} < \frac{f_{1}(x_{6})}{\lambda_{1}} \)、\( \frac{f_{2}(x_{5})}{\lambda_{2}} < \frac{f_{2}(x_{6})}{\lambda_{2}} \),所以\( g^{mtch}(x_{5}|\lambda,z^{*}) < g^{mtch}(x_{6}|\lambda,z^{*}) \),因此可以认为个体\( x_{5} \)优于个体\( x_{6} \)。
4)两个体在向量\( \overrightarrow{\lambda} \)的两侧,如图5中的\( x_{7} \)和\( x_{8} \)。此时不能确定哪个个体更优。
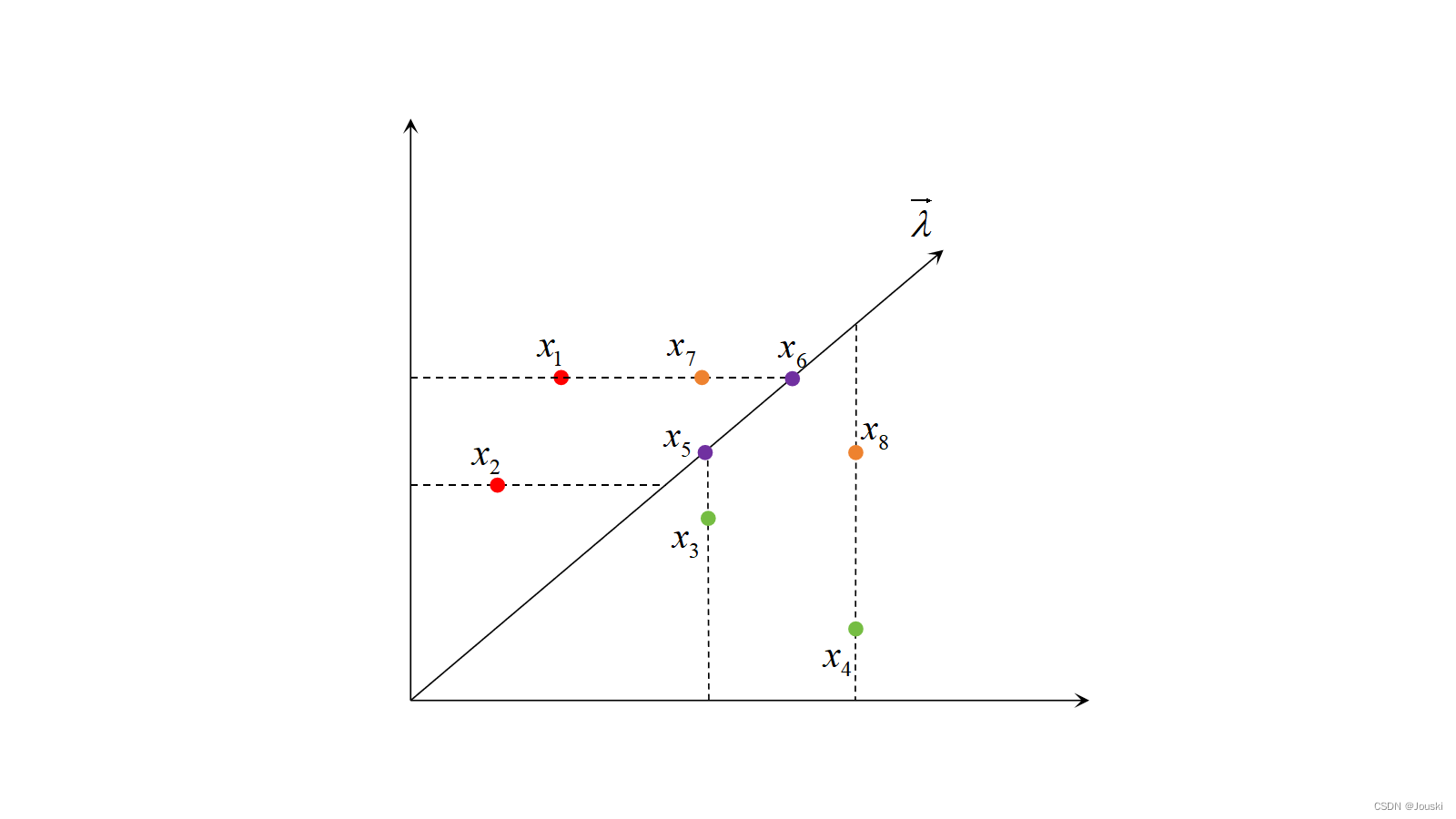
图5
综上分析,可以认为,MTCH分解法的进化方向为垂直两个坐标轴方向指向原点,如图6所示。

图6
往期内容:
基于分解的多目标进化算法MOEAD:基于分解的多目标优化算法MOEAD(一):加权和分解法的等高线理解和分析
外罚函数法:外罚函数法(一):外罚函数的构造
多目标粒子群算法:智能优化算法:多目标粒子群优化算法(MOPSO)
创作不易,点个赞再走








 本文聚焦多目标优化领域的NSGAII和MOEAD算法,着重探讨较难理解的MOEAD算法的三种分解方法。采用改进的切比雪夫分解法,通过对等高线的分析,分情况讨论向量位置关系,得出个体优劣判断及MTCH分解法的进化方向,助力理解分解策略。
本文聚焦多目标优化领域的NSGAII和MOEAD算法,着重探讨较难理解的MOEAD算法的三种分解方法。采用改进的切比雪夫分解法,通过对等高线的分析,分情况讨论向量位置关系,得出个体优劣判断及MTCH分解法的进化方向,助力理解分解策略。
















 3187
3187

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








