多目标优化算法:基于分解的多目标进化算法 MOEA/D
相关概念
- MOP-多目标优化
多目标优化问题(MOP):
m a x F ( x ) = ( f 1 ( x ) , , , f m ( x ) ) T max F(x) = (f_1(x),,,f_m(x))^T maxF(x)=(f1(x),,,fm(x))T
s u b j e c t t o x ∈ Ω subject\ to\ x \in \varOmega subject to x∈Ω
Ω \varOmega Ω是决策空间, F : Ω → R m F: \varOmega \to R^m F:Ω→Rm包含m个实数值目标函数, R m R^m Rm被称为目标空间,{ F ( x ) ∣ x ∈ Ω F(x)|x \in \varOmega F(x)∣x∈Ω}为可得到目标集合
if x ∈ R n x \in R_n x∈Rn,所有的连续目标和 Ω \varOmega Ω被描述为
Ω = { x ∈ R n ∣ h j ( x ) ≤ 0 , j = 1 , . . . , m } \varOmega =\{x \in R^n|h_j(x) \le 0,j=1,...,m\} Ω={x∈Rn∣hj(x)≤0,j=1,...,m}
MOEA/D的特点
- 将多目标问题分解成一定数量N的子问题,再同时进行优化每个子问题,简单但是有效
- 由于MOEA/D算法利用相邻子问题的解同时优化多个子问题而不是优化整体,MOEA/D对保持多样性和降低适应度分配的难度都有很好的表现
- 当MOEA/D算法当遇到种群数量较小时,也可以产生分步均匀的解。
- T为最接近的相邻子问题的数量,当T太小时,搜索域太小;当T太大时,产生的解质量会下降。
- 相比于NSGA-II和MOGLS,MOEA/D有较好的计算复杂度,MOGLS和MOEA/D在解决0-1背包问题时,使用相同的分解方法,MOEA/D的解更优。在有个3目标连续测试中,使用一个先进分解方法的MOEA/D算法的表现比NSGA-II优秀许多。
MOEA/D的分解策略
-
权重求和法(Weighted Sum Approach)
使 λ = ( λ 1 , . . . . . . , λ m ) T \lambda = (\lambda_1,......,\lambda_m)^T λ=(λ1,......,λm)T为一个权重向量,对所有的 i = 1 , . . . , m i=1,...,m i=1,...,m有 λ i ≥ 0 \lambda_i \geq 0 λi≥0且 ∑ i = 1 m = 1 \sum_{i=1}^m=1 ∑i=1m=1.对于优化问题:
m a x g w s ( x ∣ λ ) = ∑ i = 1 m λ i f i ( x ) max \ g^{ws}(x|\lambda) = \sum_{i=1}^m \lambda_if_i(x) max gws(x∣λ)=i=1∑mλifi(x)
s u b j e c t t o x ∈ Ω subject \ to \ x \in \varOmega subject to x∈Ω
当 x x x是需要被优化的变量时, λ \lambda λ在目标函数中是一个系数向量。在上面标量化的问题中,我们可以使用不同权重的 λ \lambda λ以生成一组不同的Pareto最优向量。不是每个Pareto最优向量可以通过这种方法获得非凹PFs.。 -
切比雪夫法(Tchebycheff Approach)
标量优化问题如下:
m i n g t e ( x ∣ λ , z ∗ ) = max 1 ≤ i ≤ m { λ i ∣ f i ( x ) − z i ∗ ∣ } min \ g^{te}(x|\lambda,z^*) = {\ \max_{1 \leq i \leq m}}\ \{\lambda_i|f_i(x)-z_i^*|\} min gte(x∣λ,z∗)= 1≤i≤mmax {λi∣fi(x)−zi∗∣}
s u b j e c t t o x ∈ Ω subject \ to\ x \in \varOmega subject to x∈Ω
其中 z ∗ = ( z 1 ∗ , . . . , z m ∗ ) T z^* = (z_1^*,...,z_m^*)^T z∗=(z1∗,...,zm∗)T是参照点,对于每个 i = 1 , , , m i=1,,,m i=1,,,m, z i ∗ = m a x { f i ( x ) ∣ x ∈ Ω } 3 z_i^*=max\{f_i(x)|x \in \varOmega\}^3 zi∗=max{fi(x)∣x∈Ω}3。一个能够获得不同Pareto最优解的方式是交换权重向量。一个缺点是,对于连续的MOP,使用这种方法的聚合函数不平滑。然而这种方法仍然可以使用在我们提出的EA框架中,因为我们不需要计算该聚合函数的倒数。 -
边界交叉法(Boundary Intersection)

m
i
n
g
b
i
(
x
∣
λ
,
z
∗
)
=
d
min \ g^{bi}(x|\lambda,z^*) = d
min gbi(x∣λ,z∗)=d
s
u
b
j
e
c
t
t
o
z
∗
−
F
(
x
)
=
d
λ
,
x
∈
Ω
subject\ to\ z^*-F(x) = d\lambda, \ x \in \varOmega
subject to z∗−F(x)=dλ, x∈Ω
当
λ
\lambda
λ和
z
∗
z^*
z∗分别是权重向量和参考点时,上图中约束
z
∗
−
F
(
x
)
=
d
λ
z^*-F(x)=d\lambda
z∗−F(x)=dλ保证
F
(
x
)
F(x)
F(x)这个点总是在方向为
λ
\lambda
λ且穿过
z
∗
z^*
z∗的直线L上。优化的目标是尽可能高的将F(x)推至可达到目标集合的边界上。
上述方法其中有个最大的缺点是处理相等约束。我们可以使用罚函数来解决约束问题,具体如下:

m
i
n
g
b
i
p
(
x
∣
λ
,
z
∗
)
=
d
1
+
θ
d
2
min \ g^{bip}(x|\lambda,z^*)=d_1+\theta d_2
min gbip(x∣λ,z∗)=d1+θd2
s
u
b
j
e
c
t
t
o
x
∈
Ω
subject \ to\ x \in \varOmega
subject to x∈Ω
where
d
1
=
∥
(
z
∗
−
F
(
x
)
)
T
λ
∥
∥
λ
∥
d_1 = \frac {\lVert (z^* - F(x))^T \lambda \rVert} {\lVert \lambda \rVert}
d1=∥λ∥∥(z∗−F(x))Tλ∥
a
n
d
d
2
=
∥
F
(
x
)
−
(
z
∗
−
d
1
λ
)
∥
and \ d_2 = \lVert F(x) - (z^* - d_1\lambda) \rVert
and d2=∥F(x)−(z∗−d1λ)∥
θ
>
0
\theta > 0
θ>0是一个预设的惩罚参数。
y
y
y是F(x)在直线L上的投影,
d
1
d_1
d1是
z
∗
z^*
z∗和y的距离,
d
2
d_2
d2是F(x)和L的距离。当
θ
\theta
θ去适当的值时,两种边界交叉法的结果会非常接近。
MOEA/D的算法步骤(Tchebycheff Approach)
令
λ
j
=
(
λ
1
j
,
.
.
.
,
λ
m
j
)
T
\lambda^j = (\lambda_1^j,...,\lambda_m^j)^T
λj=(λ1j,...,λmj)T为一组均匀分布的权重向量,
z
∗
z^*
z∗为参考点,第j个问题的目标函数为:
g
t
e
(
x
∣
λ
j
,
z
∗
)
=
max
1
≤
i
≤
m
{
λ
i
j
∣
f
i
(
x
)
−
z
i
∗
∣
}
g^te(x|\lambda^j,z^*)= \max_{1 \leq i \leq m}\{\lambda_i^j | f_i(x) - z_i^*|\}
gte(x∣λj,z∗)=1≤i≤mmax{λij∣fi(x)−zi∗∣}
MOEA/D可以在一次运行中,同时优化所有这N个子问题目标函数。
在MOEA/D中,权重向量的邻居中取几个最接近的权重向量,每一代的种群由每个子问题的最优解组成。只有相邻子问题可以进行优化当前的解。
每一代(t),MOEA/D(Techebycheff)包括:
- x 1 , . . . , x N ∈ Ω x^1,...,x^N \in \varOmega x1,...,xN∈Ω由N个点组织成的种群, x i x^i xi是第i个问题的当前解
- F V i , . . . , F V N FV^i,...,FV^N FVi,...,FVN, F V i = F ( x i ) FV^i = F(x^i) FVi=F(xi)
- z = ( z 1 , . . . , z m ) T z = (z_1 , ... ,z_m)^T z=(z1,...,zm)T, z i z_i zi是目标 f i f_i fi中已发现最好的值。
- EP用来存储咋搜索过程中的非支配解
Input:
- MOP(1);
- 算法停止条件
- N:分解成的子问题的个数
- N个分布均匀的权重向量
- T:每个权重向量相邻的权重向量的个数
Output:EP
Step 1) 初始化:
Step 1.1) Set EP =
∅
\empty
∅。
Step 1.2) 计算任意两个权重向量的欧氏距离,找出每个权重向量最近邻的T个权重向量,对每一个 i = 1 , . . . , N i = 1,...,N i=1,...,N,设$B(i) = {i_1,…,i_T}, 其 中 其中 其中 \lambda{i1},…,\lambda{iT} 是 最 接 近 是最接近 是最接近\lambda^i$的N个权重向量。
Step 1.3) 随机或者使用特定方法生成一个初始化种群 x 1 , . . . , x N x^1,...,x^N x1,...,xN。设 F V i = F ( x i ) FV^i = F(x^i) FVi=F(xi)。
Step 1.4) 根据特定的问题初始化 z = ( z 1 , . . . , z m ) T z = (z_1,...,z_m)^T z=(z1,...,zm)T。
Step 2) 更新:
循环对
i
=
1
,
.
.
.
,
N
i=1,...,N
i=1,...,N做以下操作
Step 2.1)繁殖: 从
B
(
i
)
B(i)
B(i)中随机选择两个索引
k
,
l
k,l
k,l,
x
k
x^k
xk和
x
l
x^l
xl使用遗传算子生成新的解
y
y
y。
Step 2.2)改善: 根据特定问题,使用启发式方法改进 y y y生成 y ′ y' y′。
Step 2.3)更新z: 对于每一个$j = 1 , …,m , 如 果 ,如果 ,如果z_j < f_i(y’) , 使 ,使 ,使z_j = f_j(y’)$。
Step 2.4)更新邻域解: 对每个属于 B ( i ) B(i) B(i)的索引j,如果 g t e ( y ′ ∣ λ j , z ) ≤ g t e ( x j ∣ λ j , z ) g^{te}(y'|\lambda^j,z) \leq g^{te}(x^j|\lambda^j,z) gte(y′∣λj,z)≤gte(xj∣λj,z),则令 x j = y ′ x^j = y' xj=y′ , F V j = F ( y ′ ) FV^j = F(y') FVj=F(y′)。
Step 2.5)更新EP:
1.删除EP中所有被
F
(
y
′
)
F(y')
F(y′)支配的向量。
2.如果EP中没有向量支配
F
(
y
′
)
F(y')
F(y′),则将
F
(
y
′
)
F(y')
F(y′)加入到EP中。
Step 3)停止条件: 如果满足停止条件,停止并且输出EP,否则则跳转至Step 2。
MOEA/D与NSGA-II的对比
- 评价准则
1.1 C-Metric
A和B是MOP问题的两个接近的PF集合
C
(
A
,
B
)
=
∣
{
u
∈
B
∣
∃
v
∈
A
:
v
d
o
m
i
n
a
t
e
s
u
}
∣
∣
B
∣
C(A,B) = \frac {\lvert \{u \in B | \exist v \in A: v dominates \ u \} \rvert} {\lvert B \rvert}
C(A,B)=∣B∣∣{u∈B∣∃v∈A:vdominates u}∣
C
(
A
,
B
)
C(A,B)
C(A,B)不等于
1
−
C
(
B
,
A
)
1-C(B,A)
1−C(B,A)。
C
(
A
,
B
)
=
1
C(A,B) = 1
C(A,B)=1表示B中所有的解都被A中的一些解支配。当
C
(
A
,
B
)
=
0
C(A,B)=0
C(A,B)=0表示B中没有解被A中支配。
1.2 D-Metric
令
P
∗
P^*
P∗为沿着PF的一组分布均匀的点,令A为接近PF的集合,
P
∗
P^*
P∗和A的平均距离定义如下:
D
(
A
,
P
∗
)
=
∑
v
∈
P
∗
d
(
v
,
A
)
∣
P
∗
∣
D(A,P^*) = \frac {\displaystyle\sum_{v \in P^*}d(v,A)} {\lvert P^* \rvert}
D(A,P∗)=∣P∗∣v∈P∗∑d(v,A)
d
(
v
,
A
)
d(v,A)
d(v,A)是
v
v
v和A中的点之间的最小欧氏距离。如果
∣
P
∗
∣
\lvert P^* \rvert
∣P∗∣足够大,说明集合很好的代表了PF,
D
(
A
,
P
∗
)
D(A,P^*)
D(A,P∗)可以一定程度上评估A的多样性和收敛性。
- MOEA/D与NSGA-II的对比
2.1 时间复杂度对比
采用改良的MOEA/D进行实验,去掉了额外种群EP,因此去掉步骤2.5,去掉了启发式优化过程,因此删去了步骤2.2,所以时间复杂度主要在步骤2部分。步骤2.3进行了
O
(
m
)
O(m)
O(m)次比较,步骤2.4部分的时间复杂度为
O
(
m
T
)
O(mT)
O(mT),由于分成了N个子问题,所以改良的MOEA/D的时间复杂度为
O
(
m
T
N
)
O(mTN)
O(mTN)。而NSGA-II的时间复杂度为
O
(
m
N
2
)
O(mN^2)
O(mN2)。因为N为权重向量的个数,而T为一个权重向量相邻的权重向量的个数,所以
T
<
N
T < N
T<N,故而MOEA/D的时间复杂度比NSGA-II要小,但时间复杂度的优势不是非常明显。
2.2 空间复杂度对比
改良后的MOEA/D没有EP,只有m个参照点z需要存储,但是与一代种群大小相比,所占空间非常小,我觉得两者是空间复杂度上没有特别大的差别。
2.3 测试函数及实验结果
根据论文中,针对2个目标问题将NSGA-II和MOEA/D的种群大小都100。针对3目标问题,种群数都设为300,都采用模拟二进制的交叉变异和多项式变异,
p
c
=
1.0
,
p
m
=
1
/
n
,
T
=
20
p_c=1.0,p_m=1/n,T=20
pc=1.0,pm=1/n,T=20
- ZDT1
f
1
(
X
)
=
x
1
f_1(X) = x_1
f1(X)=x1
f
2
(
X
)
=
g
(
X
)
[
1
−
x
1
/
g
(
X
)
]
f_2(X) = g(X)[1-\sqrt{x_1/g(X)}]
f2(X)=g(X)[1−x1/g(X)]
g
(
X
)
=
1
+
9
(
∑
i
=
2
n
x
i
)
/
(
n
−
1
)
g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1)
g(X)=1+9(i=2∑nxi)/(n−1)
n
=
30
,
n=30,
n=30,
x
1
∈
[
0
,
1
]
,
x
i
=
0
x_1\in[0,1],x_i = 0
x1∈[0,1],xi=0
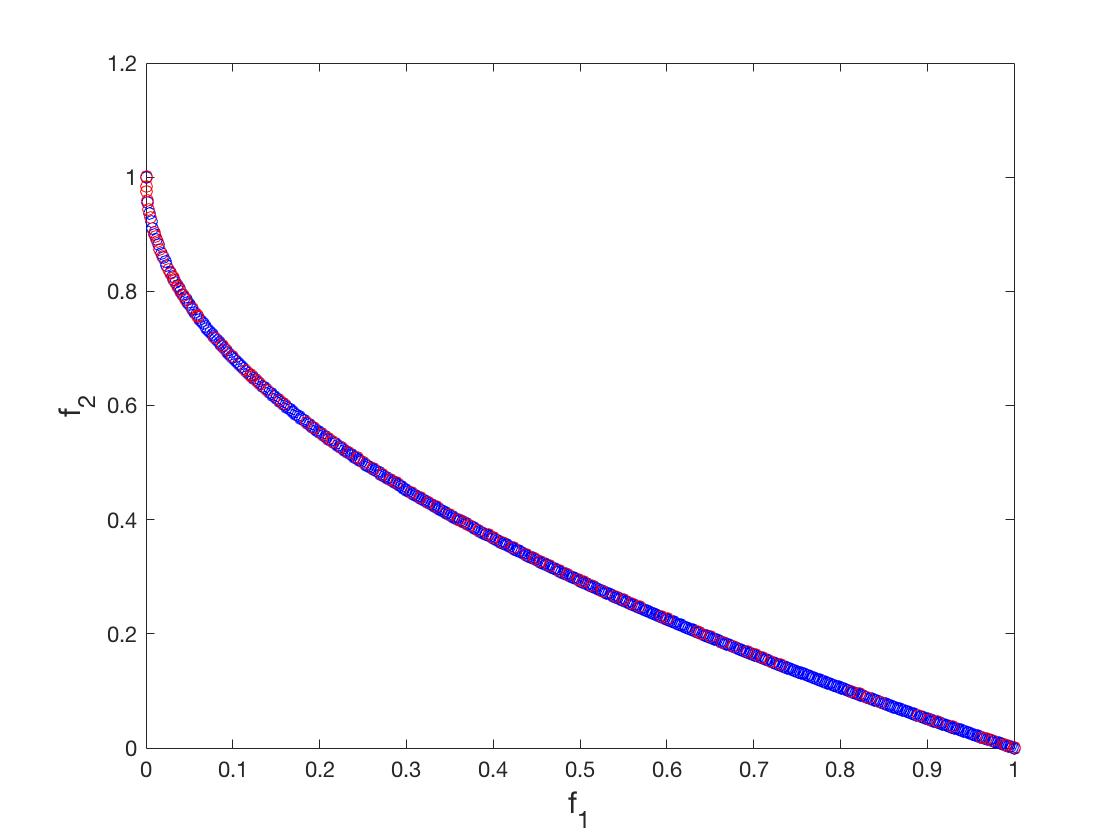
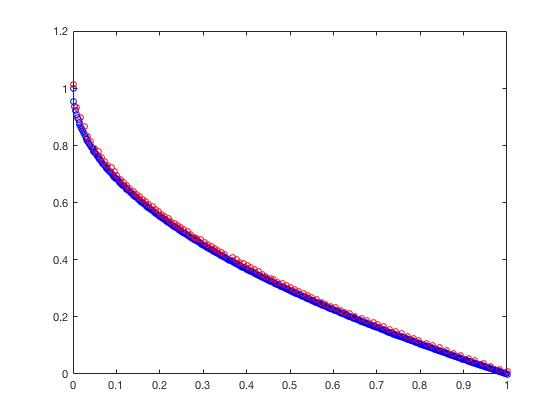
- ZDT2
f
1
(
X
)
=
x
1
f_1(X) = x_1
f1(X)=x1
f
2
(
X
)
=
g
(
X
)
[
1
−
(
x
1
/
g
(
X
)
)
2
]
f_2(X) = g(X)[1-(x_1/g(X))^2]
f2(X)=g(X)[1−(x1/g(X))2]
g
(
X
)
=
1
+
9
(
∑
i
=
2
n
x
i
)
/
(
n
−
1
)
g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1)
g(X)=1+9(i=2∑nxi)/(n−1)
n
=
30
,
n=30,
n=30,
x
1
∈
[
0
,
1
]
,
x
i
=
0
x_1\in[0,1],x_i = 0
x1∈[0,1],xi=0
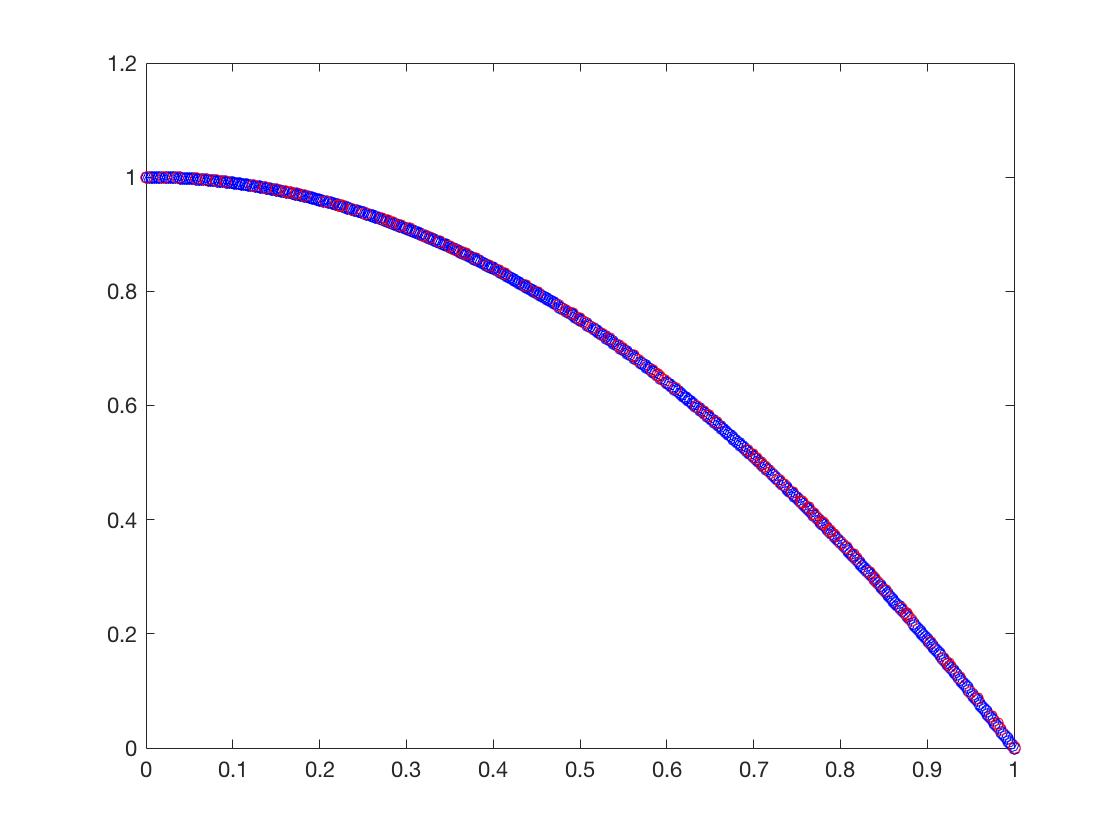
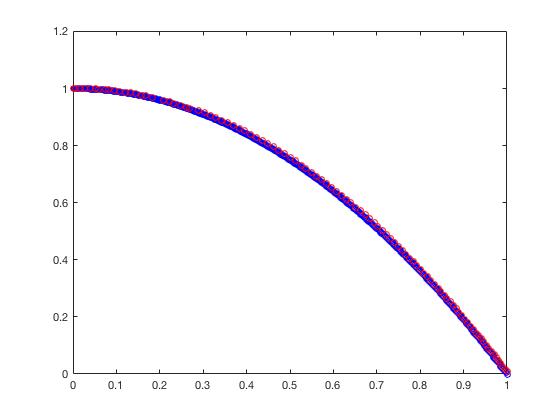
- ZDT3
f
1
(
X
)
=
x
1
f_1(X) = x_1
f1(X)=x1
f
2
(
X
)
=
g
(
X
)
[
1
−
x
1
/
g
(
X
)
−
x
1
g
(
X
)
sin
(
10
π
x
1
)
]
f_2(X) = g(X)[1-\sqrt{x_1/g(X)}-{\frac{x_1}{g(X)}}\sin(10\pi x_1)]
f2(X)=g(X)[1−x1/g(X)−g(X)x1sin(10πx1)]
g
(
X
)
=
1
+
9
(
∑
i
=
2
n
x
i
)
/
(
n
−
1
)
g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1)
g(X)=1+9(i=2∑nxi)/(n−1)
n
=
30
,
n=30,
n=30,
x
1
∈
[
0
,
1
]
,
x
i
=
0
x_1\in[0,1],x_i = 0
x1∈[0,1],xi=0
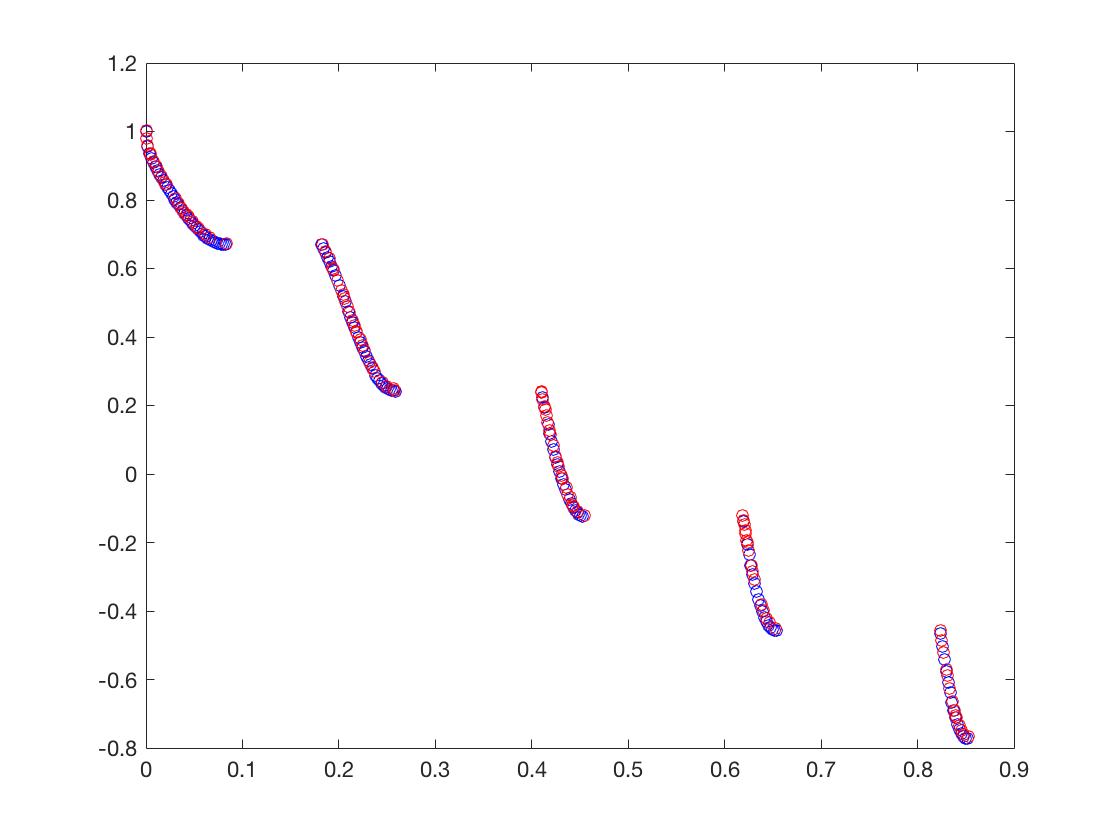
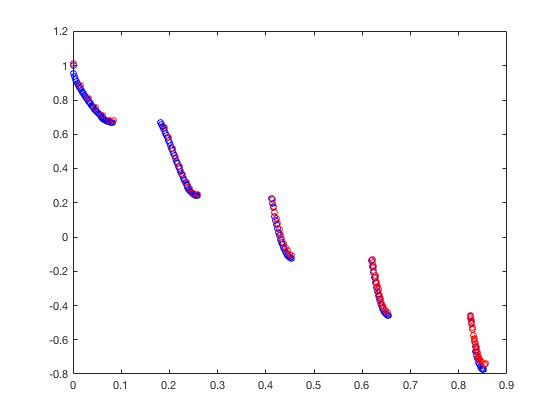
- ZDT4
f
1
(
X
)
=
x
1
f_1(X) = x_1
f1(X)=x1
f
2
(
X
)
=
g
(
X
)
[
1
−
x
1
/
g
(
X
)
]
f_2(X) = g(X)[1-\sqrt{x_1/g(X)}]
f2(X)=g(X)[1−x1/g(X)]
g
(
X
)
=
1
+
10
(
n
−
1
)
+
∑
i
=
2
n
[
x
i
2
−
10
cos
(
4
π
x
i
)
]
g(X) = 1+10(n-1)+\sum_{i=2}^n[x_i^2-10\cos(4\pi x_i)]
g(X)=1+10(n−1)+i=2∑n[xi2−10cos(4πxi)]
n
=
10
,
n=10,
n=10,
x
1
∈
[
0
,
1
]
,
x
i
=
0
x_1\in[0,1],x_i = 0
x1∈[0,1],xi=0
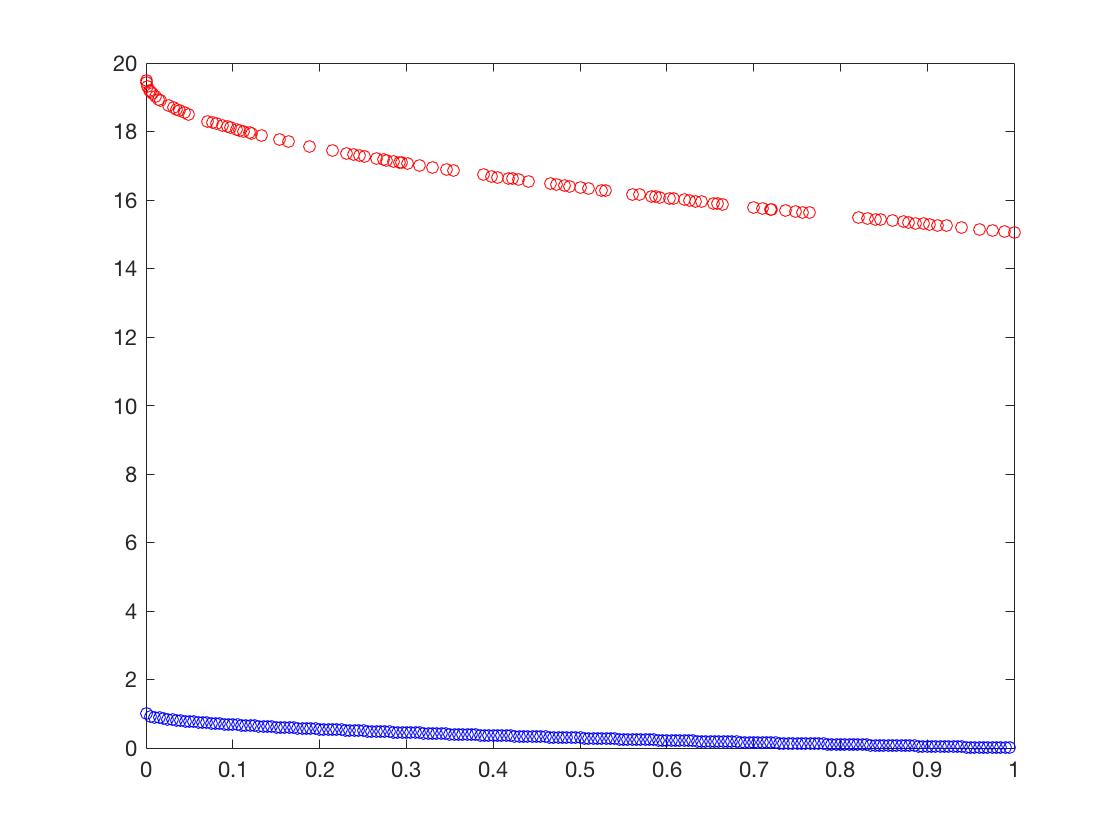
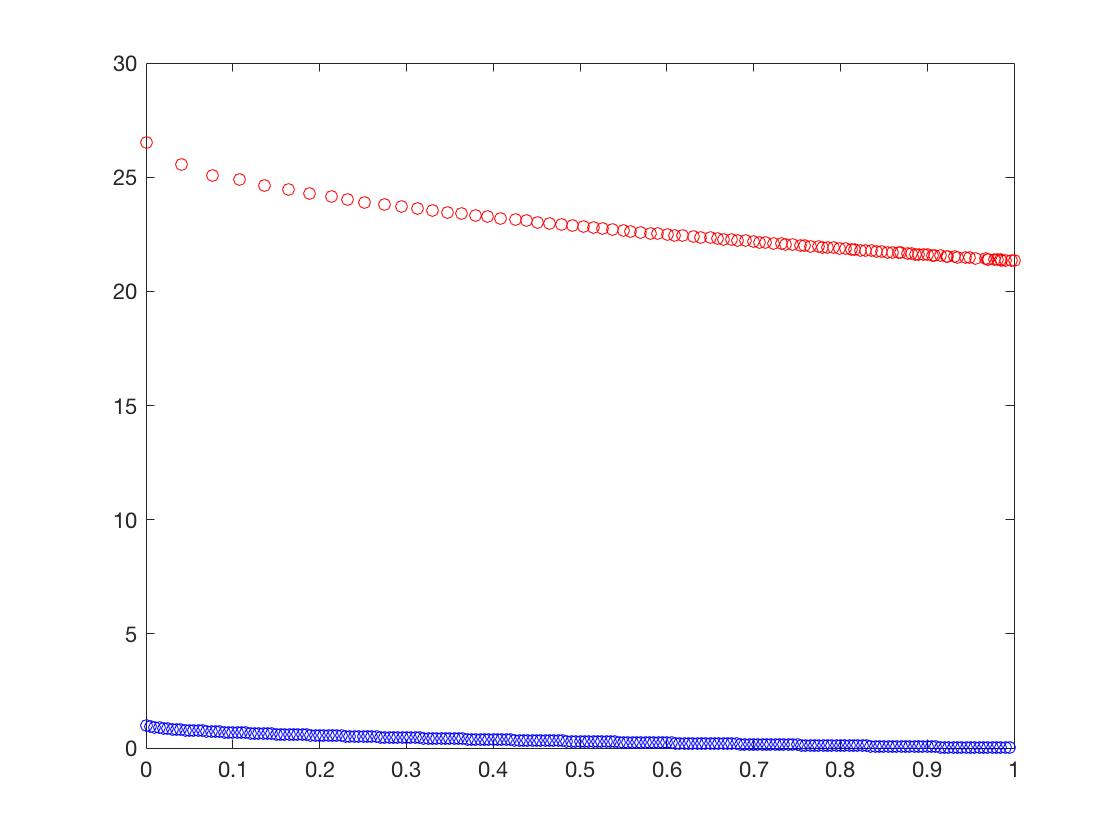
- ZDT6
f
1
(
X
)
=
1
−
e
x
p
(
−
4
π
x
1
)
sin
6
(
6
π
x
1
)
f_1(X)= 1-exp(-4\pi x_1)\sin^6(6\pi x_1)
f1(X)=1−exp(−4πx1)sin6(6πx1)
f
2
(
X
)
=
g
(
X
)
[
1
−
(
f
1
(
X
)
/
g
(
X
)
)
2
]
f_2(X)= g(X)[1-(f_1(X)/g(X))^2]
f2(X)=g(X)[1−(f1(X)/g(X))2]
g
(
X
)
=
1
+
9
[
(
∑
n
i
=
2
x
i
)
/
(
n
−
1
)
]
0.25
g(X) = 1+9[(\sum_n^{i=2}x_i)/(n-1)]^{0.25}
g(X)=1+9[(n∑i=2xi)/(n−1)]0.25
n
=
10
,
n=10,
n=10,
x
1
∈
[
0
,
1
]
,
x
i
=
0
x_1\in[0,1],x_i = 0
x1∈[0,1],xi=0
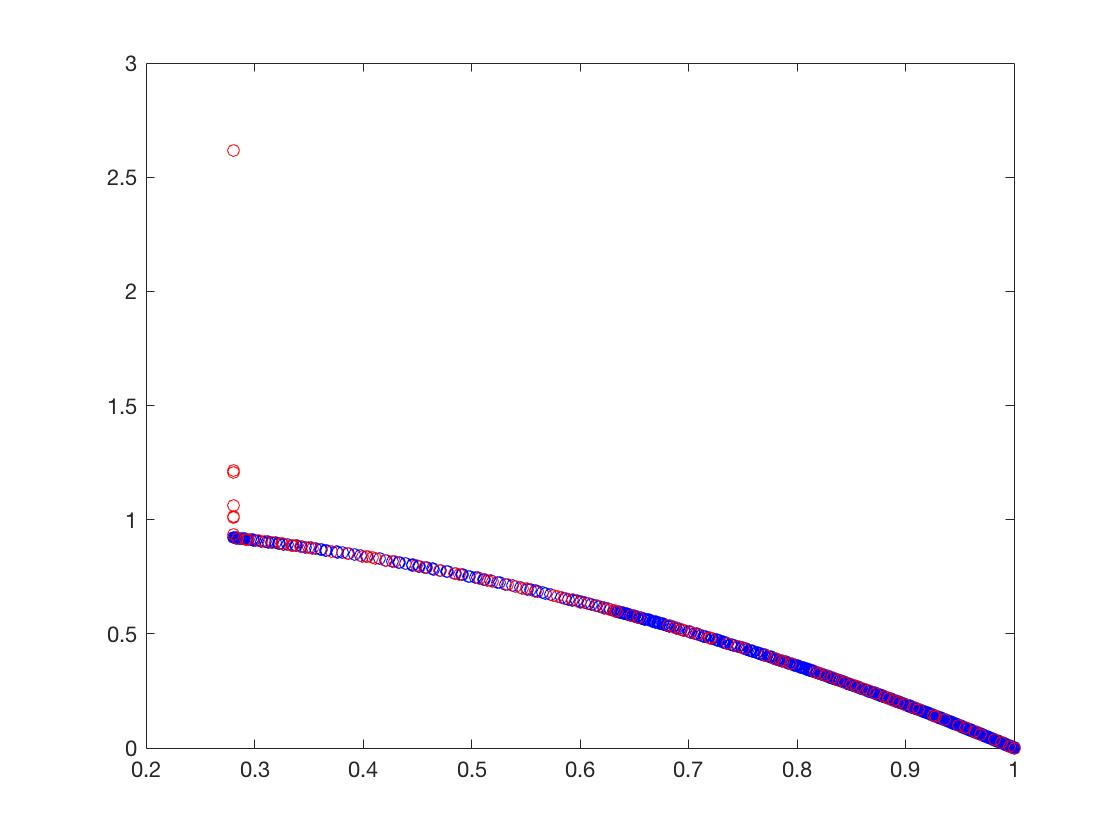
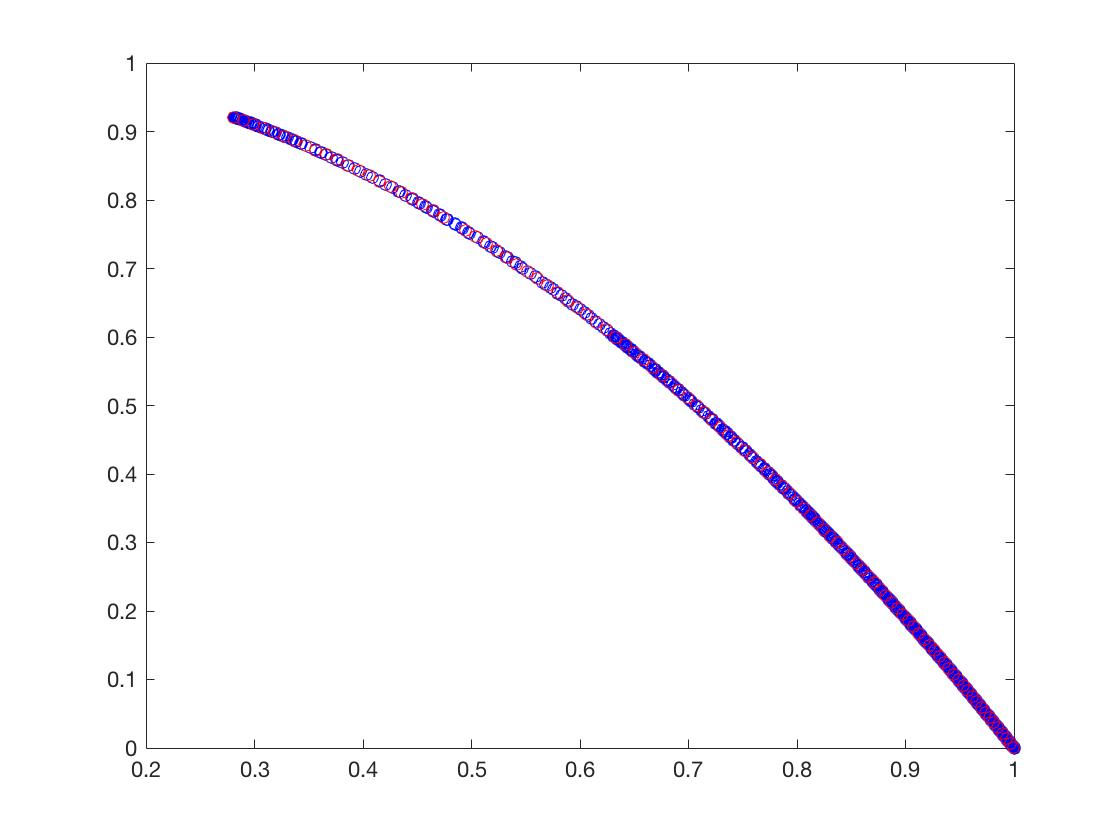
- DTLZ1
f 1 ( X ) = ( 1 + g ( X ) ) x 1 x 2 f_1(X) = (1+g(X))x_1x_2 f1(X)=(1+g(X))x1x2
f 2 ( X ) = ( 1 + g ( X ) ) x 1 ( 1 − x 2 ) f_2(X) = (1+g(X))x_1(1-x_2) f2(X)=(1+g(X))x1(1−x2)
f 3 ( X ) = ( 1 + g ( X ) ) ( 1 − x 1 ) f_3(X) = (1+g(X))(1-x_1) f3(X)=(1+g(X))(1−x1)
g ( X ) = 100 ( n − 2 ) + 100 ∑ i = 3 n { ( x i − 0.5 ) 2 − cos [ 20 π ( x i − 0.5 ) ] } g(X) = 100(n-2)+100\sum_{i=3}^n\{(x_i-0.5)^2-\cos[20\pi(x_i-0.5)]\} g(X)=100(n−2)+100i=3∑n{(xi−0.5)2−cos[20π(xi−0.5)]}
x = ( x 1 , . . . , x n ) T ∈ [ 0 , 1 ] n x = (x_1,...,x_n)^T \in [0,1]^n x=(x1,...,xn)T∈[0,1]n
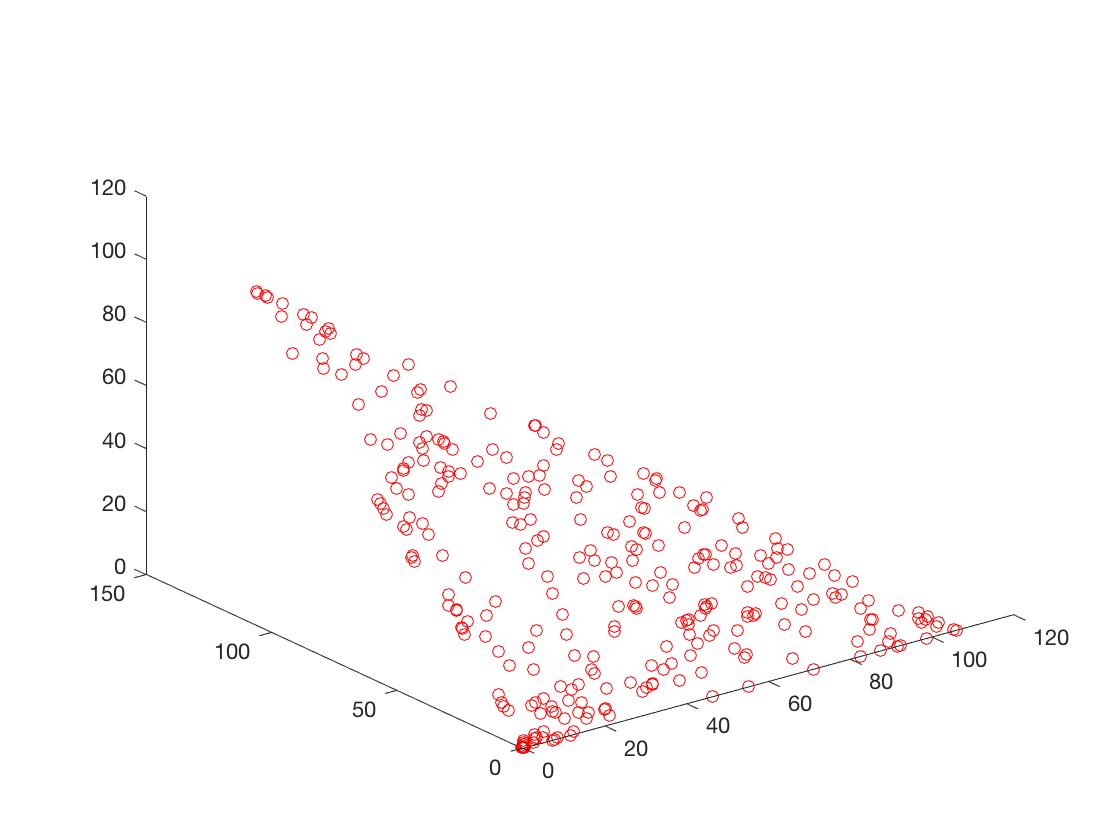
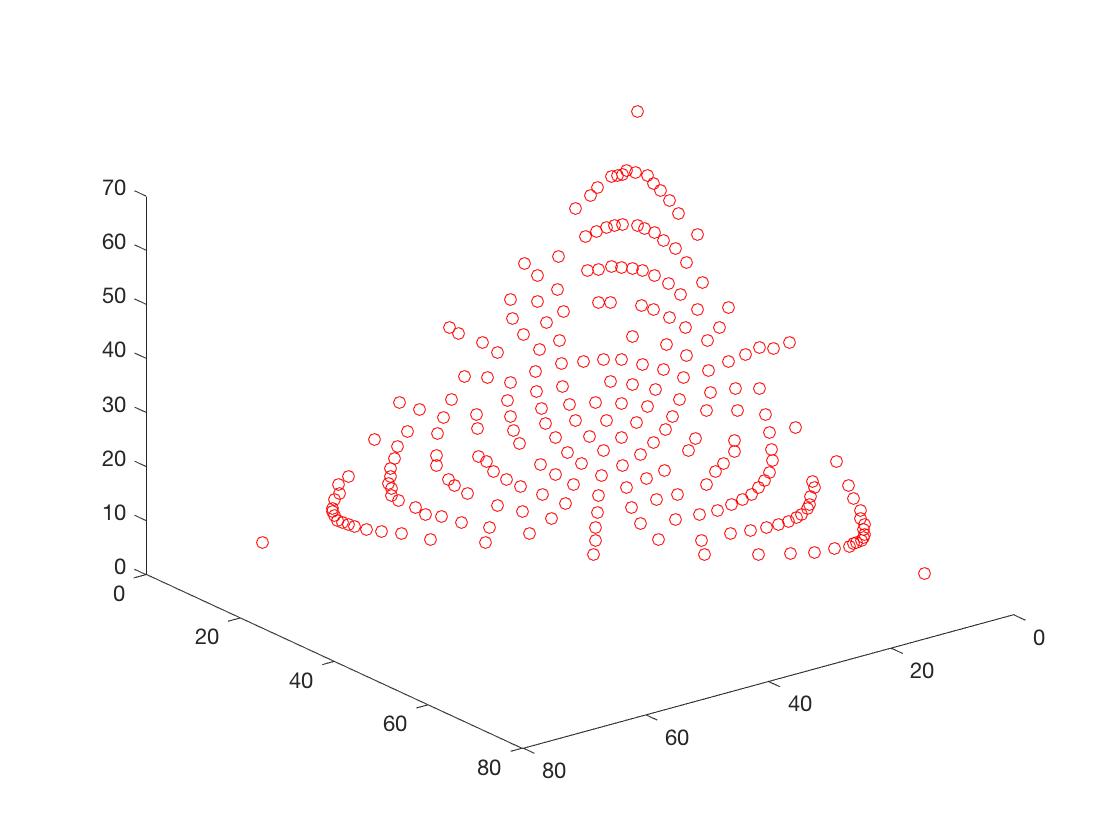
- DTLZ2
f 1 ( X ) = ( 1 + g ( X ) ) cos ( x 1 π 2 ) cos ( x 2 π 2 ) f_1(X) = (1+g(X))\cos(\frac {x_1\pi} {2})\cos(\frac {x_2\pi} {2}) f1(X)=(1+g(X))cos(2x1π)cos(2x2π)
f 2 ( X ) = ( 1 + g ( X ) ) cos ( x 1 π 2 ) sin ( x 2 π 2 ) f_2(X) = (1+g(X))\cos(\frac {x_1\pi} {2})\sin(\frac {x_2\pi} {2}) f2(X)=(1+g(X))cos(2x1π)sin(2x2π)
f 3 ( X ) = ( 1 + g ( X ) ) sin ( x 1 π 2 ) f_3(X) = (1+g(X))\sin(\frac {x_1\pi} {2}) f3(X)=(1+g(X))sin(2x1π)
g ( X ) = ∑ i = 3 n x i 2 g(X)=\sum_{i=3}^nx_i^2 g(X)=i=3∑nxi2
x = ( x 1 , . . . , x 2 ) T ∈ [ 0 , 1 ] 2 ∗ [ − 1 , 1 ] n − 2 x = (x_1,...,x_2)^T \in [0,1]^2*[-1,1]^{n-2} x=(x1,...,x2)T∈[0,1]2∗[−1,1]n−2
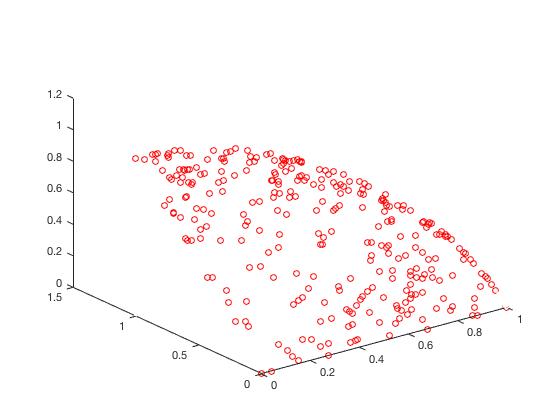
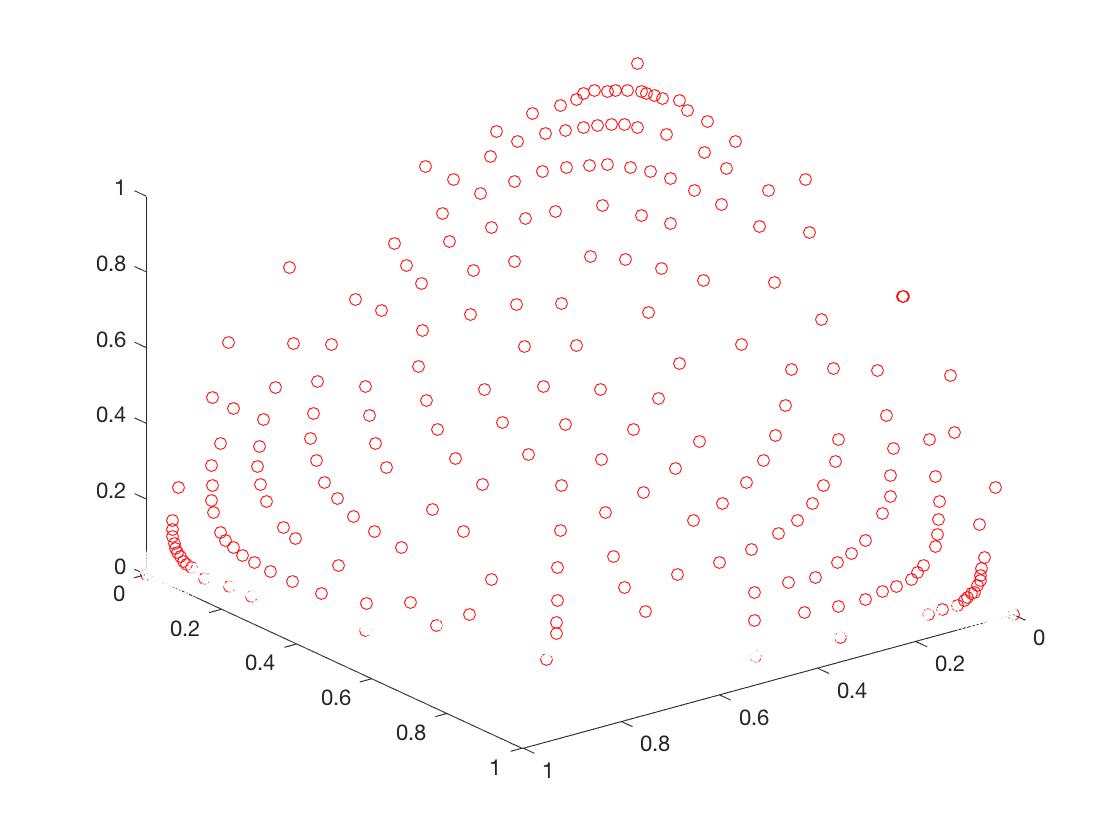
Δ \Delta Δ的Mean
| Problem | ZDT1 | ZDT2 | ZDT3 | ZDT4 | ZDT6 | DTLZ1 | DTLZ2 |
|---|---|---|---|---|---|---|---|
| NSGA-II | 0.642 | 0.706 | 0.425 | 1.00 | 0.610 | 0.945 | 0.0323 |
| MOEA/D | 1.00 | 1.00 | 0.931 | 1.00 | 0.041 | 0.830 | 0.0281 |
γ \gamma γ的Mean
| Problem | ZDT1 | ZDT2 | ZDT3 | ZDT4 | ZDT6 | DTLZ1 | DTLZ2 |
|---|---|---|---|---|---|---|---|
| NSGA-II | 0.00574 | 0.0662 | 0.00614 | 29.299 | 0.00397 | 72.558 | 0.07819 |
| MOEA/D | 0.0177 | 0.4017 | 0.0135 | 15.672 | 0.00635 | 44.726 | 0.4634 |
可以从图的对比和表中 Δ \Delta Δ与 γ \gamma γ两个参数的对比看出,在两目标问题上,两者算法相差不多,甚至在ZDT1、ZDT2、ZDT3等问题上NSGA-II更优一些,但是在ZDT6上MOEA/D表现的更好,MOEA/D的主要优势在算法的计算速度上,在面对三目标问题时,MOEA/D比NSGA-II要优秀很多。
























 1852
1852

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








