如何增加无人机的飞行时间和升力？

目录

1. 介绍和假设。
2. 无人机是如何飞行的？
3. 什么是螺旋桨的效率？
4. 如何为四旋翼无人机选择最高效的螺旋桨？
5. 如何选择最高效的电机？
6. 如何选择电调？
7. 如何计算无人机飞行时间（带计算器）？

介绍和假设

无人机的设计优化是一个循环往复的过程，为了方便描述上述过程，我们假设已经拥有了一台成功起飞的无人机，并获知了无人机的重量和电池尺寸，另外说明下假定的这台多旋翼无人机不是竞速类或是竞技类的无人机。

为了更详细具体的描述优化过程，我们将以代表绝大多数无人机的Otus Quadcopter为例。

图1

 我们初步选定的四旋翼无人机主要技术配置如下：

• 4个螺旋桨：Gemfan 5040
• 4台电机：Hypetrain 2207-2450Kv 电机
• 4台电调：Afro 20A Race Spec Mini ESC with BEC
• 1节电池：Turnigy nano-tech 1300mAh 4S 45~90C Lipo Pack
• 无人机框架和净载荷

基于上述技术配置，上述无人机当前的飞行时间是4分钟。

无人机是如何飞行的？

第一步我们需要了解无人机如何才能起飞和航行。无人机起飞需要克服自身的重力和空气阻力，其重力是自身质量和重力加速度（g）的乘积，空气阻力则取决于无人机自身的参考面积、空气密度和风速等综合条件因素。

螺旋桨的旋转产生拉力使得无人机上升并保持飞行状态，当无人机悬停时，我们可以假设此时螺旋桨的总拉力等于无人机的重力。

依据上述假设和无人机总重量，如果要保持无人机的悬停状态，我们可以计算出每个螺旋浆需要提供的拉力。已知无人机的质量是777g，因此我们需要7.6N的总拉力，即单个螺旋桨为1.9N。

图2：无人机重量和悬停拉力要求

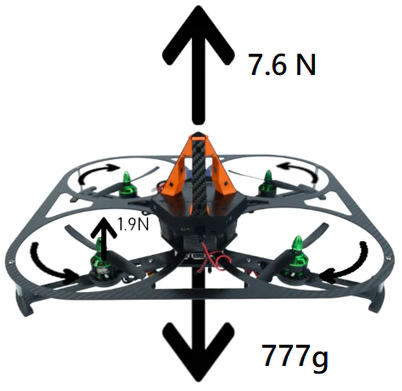
为确保无人机有更好的操控性，理论上螺旋桨提供的最大拉力应至少为悬停时拉力的两倍左右。以上建议仅供参考，因为竞速类四旋翼无人机会要求有更高的推重比。

我们开始选择具有最高效率的螺旋桨，可以提供1.9N的拉力，最大尺寸6英寸，可提供最大3.8N的峰值拉力。

我们可以根据螺距、尺寸、材料和品牌等变量因素选择螺旋桨，以此最终选定最高效的推进系统。

什么是螺旋浆的效率？

螺旋桨的作用是将电机输出的机械能转化为拉力，其效率是螺旋桨的输出（主要是拉力）与输入（电机的机械功率）的比值。

正如之前文章的介绍，电机输出的机械功率是扭矩和转速的乘积。

如何为四旋翼无人机选择最高效的螺旋桨？

依据螺旋桨技术规格数据初步选定螺旋桨，但由于目前螺旋桨的测试缺乏统一标准，用户无法有效比对不同厂商提供的技术规格。制造商通常会提供最简要的技术规格，因此建议用户在购买前应多了解下螺旋桨的预期性能。为此我们编制了无人机电机、螺旋桨和ESC的数据库帮助用户在购买螺旋桨前轻松地评估其性能。

同时用户可使用我们的1780系列测试台和相同的无人机电机去测试所有的螺旋桨，并记录其拉力、扭矩、电压、电流、电机转速和振动等测量参数。用户还可以使用测试脚本文件借助测试台软件的数据库上传功能完成螺旋桨的自动化测试过程。

我们需要测量拉力、扭矩和转速等性能，当系统的控制变量是扭矩和转速时，螺旋桨测试的数据变化往往独立于电机的数据变化。因为螺旋桨的拉力取决于螺旋桨的转速和空气流速，而不是单取决于提供动力的电机。所以无论用户选取哪款电机，螺旋桨在特定转速下产生的拉力都是相同的。我们可以根据上述规律检查测试过程是否正确。当使用多台电机测试单个螺旋桨产生的拉力和转速的对应数据都应该非常接近下图中的同一条曲线。

图3

当用户确定了无人机悬停时所需的最高效螺旋桨的扭矩和转速后，即可搜索上述扭矩和转速条件下最高效率的电机。首先第一步我们需要先选定我们需要的螺旋桨。

为了简化测试过程，我们只选择其中的3款螺旋桨，并使用1580系列测试台进行测试。

• 6030R Gemfan =>直径：6英寸，节距：3英寸，重量2.22克
• 6040R King Kong =>直径：6英寸，节距：4英寸，重量3.38克
• 5040R Gemfan =>直径：5英寸，间距：4英寸，重量3.00克

图4：我们的3个候选螺旋桨

用户可以手动测试上述测试过程，还可以使用我们的脚本文件进行自动化测试。我们在测试过程中使用了脚本文件，并将测量结果与我们无人机动力数据库中的数据进行了对比分析。以下是螺旋桨机械效率（N/W）相对于拉力（N）的函数变化。

图5

如图5所示，拉力在1.9N时效率最高的螺旋桨是Gemfan 6030，效率值为0.077N/W。据此我们可以排除另外两款螺旋桨。

图6：Gefman 6030的拉力和扭矩与转速的关系

当拉力为1.9N时，Gemfan 6030的运行转速达到1300rad/s，同时产生的扭矩为0.0184Nm。（图6） 

如何选择最高效的电机？

当确定螺旋桨的选型后，我们接下来可以选定扭矩为0.0184 Nm和转速为1300 rad/s时效率最高的电机。同样为了简化过程，我们只选用2款不同的电机用以测试，在现实过程中我们会在多款电机中选定最优款。

图7：Gefman 6030螺旋桨和我们的2个候选电机

图8中显示了待测电机在配备Gemfan 6030螺旋桨时的机械效率，当拉力为1.9N时，Multistar的效率为68%，而EMAX的效率为60%。据此我们得出结论，无人机配备上述特定螺旋桨时最高效的电机是Multistar Elite 2306。

图8：悬停拉力为1.9 N时的电机效率比较

通过上图我们可直观的发现两个电机在扭矩-转速上的效率差异，但并不意味着Multistar是更好的电机，只能代表对于这款螺旋桨性能更好。若更换其他的螺旋桨，有可能Emax电机具备优的性能。

另外我们还需要确认的是Multistar电机提供的峰值拉力可以满足对无人机较好的操控性要求。正如我们起初假设的需求，要求提供的持续拉力为1.9N，同时还可以达到3.8N的峰值拉力。

图9：验证电机是否满足拉力和扭矩要求

我们通过图表直观的表现形式确认选定电机可以满足3.8N的峰值拉力要求。当达到3.8N的峰值拉力时的转速为1783rad/s，扭矩为0.035Nm。

如何选择电调？

当确定好电机和螺旋桨的选型后，我们开始选定合适的电调。目前看来，能够提供电机峰值电流为7安培且具有安全系数的ESC即可满足我们的要求。于是我们决定选择支持20安培的Afro Race Spec Mini ESC。关于电调我们也可以进行一些优化设计，相关内容本文在这里不做进一步说明。

图10

如何计算无人机的续航时间？

最后我们可以通过收集到的信息来计算无人机的续航时间。无人机的电池容量（Ebattery in Wh）等于续航时间（FT）和功率（单位：W）的乘积：

电池容量（Ebattery）等于电池质量（Wbattery，单位为克）和能量密度（sigmabattery，单位为Wh/g）的乘积：

系统总功率（Power in Watt）等于无人机的质量（Wdrone (g) = Wframe (g) + Wbattery (g)）除以螺旋桨效率（propefficiency in g/W）：

螺旋桨效率是无人机的总质量除以螺旋桨数量的一个相关计算方程。

综合上述所有方程，我们可以计算得到无人机的飞行时间如下：

不难发现，螺旋桨的效率会随着电池质量的增加而减小。而电池对飞行时间的影响是双向的，一方面电池容量更大会增加飞行时间，另一方面确使得无人机总质量增加，需要提供更大的拉力，从而又减少了飞行时间。图11直观地显示了如何在电池容量和质量间找到最佳平衡点。 

图11：无人机飞行时间与电池容量的关系

结论

在本文中，我们介绍了如何为我们的无人机选择螺旋桨、电机、电调和电池，并研究了如何比较效率、分析数据和计算续航时间。

所有这些修改都会改变无人机的总重量，尤其是在您选择其他电池的情况下。如果您明显改变无人机的重量，您可能需要重新开始分析。

正如我们在文章开头提到的，无人机的设计优化是一个循环往复的过程，需要不断重复测试了解我们的组件和性能：先做出假设，根据这些假设选择零件，测试系统，更换零件并不断重复该过程。

图12