1. 什么是BA优化
BA优化,全称Bundle Adjustment,是一种在视觉重建
中提炼出最优的3D模型和相机参数(包括内参数和外参数)的技术。它通过调整相机姿态和特征点的空间位置,使得从每一个特征点反射出的光线(bundles of lightrays)在调整后能够汇聚到相机光心,从而实现对多段相机的位姿和位姿下的路标点的空间坐标进行优化。
2. 问题背景
首先我们已经通过了pnp等方法得到了第
k
k
k帧相机到第
k
+
1
k+1
k+1帧相机的
R
R
R和
t
t
t,但是呢,我并没有安于现状,我就在想这个结果能不能再精确一点,于是我就通过第
k
k
k帧的相机坐标系结合之前求的
R
R
R和
t
t
t求出了第
k
+
1
k+1
k+1帧的相机坐标,再根据第
k
+
1
k+1
k+1帧的相机坐标解出了像素坐标,最后我用这个解出的像素坐标和真正的第
k
+
1
k+1
k+1帧相机观测到的像素坐标做差值,我希望可以通过让这个差值尽可能小来优化我的
R
R
R和,这种情况也叫重投影误差,这么长的一段话可以用个公式来表达:
e
=
p
2
−
1
z
c
2
K
P
c
2
=
p
2
−
1
z
c
2
T
P
c
1
(1)
e=p_2-\frac{1}{z_{c2}}KP_{c2}=p_2-\frac{1}{z_{c2}}TP_{c1}\tag{1}
e=p2−zc21KPc2=p2−zc21TPc1(1)
其中:
- p 2 p_2 p2:第 k + 1 k+1 k+1帧的像素坐标
- z c 2 z_{c2} zc2:第 k + 1 k+1 k+1帧的特征点深度
- P c 1 P_{c1} Pc1:第 k k k帧的特征点在相机坐标系的坐标
- T T T:第 k + 1 k+1 k+1帧和第 k k k帧之间的变换矩阵
- 题外话: R R R和 t t t不就是根据像素点 p 1 p_1 p1和 p 2 p_2 p2所求得的吗,如果是这样的话,那么(1)式不就始终为0了吗?
- 实际上, R R R和 t t t确实是根据 p 1 p_1 p1和 p 2 p_2 p2所求得的,但是又不止它们一对特征点,由pnp的知识可知至少需要三对特征点,如果是根据包含 p 1 p_1 p1和 p 2 p_2 p2这一对特征点在内的三对特征点所求的的 R R R和 t t t,那么(1)式就不是始终为0了。
3. 最小化误差
3.1. 对误差求导
3.1.1. 误差对位姿求导
观察(1)式,其中有旋转矩阵,对旋转矩阵直接求导是非常困难的,所以有必要将其转换成李代数,即 将(1)化为:
e
=
p
2
−
1
z
c
2
K
P
c
2
=
p
2
−
1
z
c
2
e
x
p
(
ξ
)
P
c
1
(2)
e=p_2-\frac{1}{z_{c2}}KP_{c2}=p_2-\frac{1}{z_{c2}}exp(\xi)P_{c1}\tag{2}
e=p2−zc21KPc2=p2−zc21exp(ξ)Pc1(2)
根据李代数的求导扰动模型

T T T代表变换矩阵, ξ \xi ξ代表李代数也就是旋转向量, p p p代表的是像素坐标, δ \delta δ則表示扰动系数,这个求导式子的意义是,对 T T T做一次扰动,那么这个式子表示 T T T对扰动的变化率,要是变化率小,则表示 T T T的置信度高
所以考虑误差 e e e的扰动模型
∂ e ∂ δ ξ = ∂ e ∂ P c 2 ∂ P c 2 ∂ δ ξ = ∂ e ∂ P c 2 ∂ T P c 1 ∂ δ ξ (3) \frac{\partial e}{ \partial \delta \xi} = \frac{\partial e}{\partial P_{c2}}\frac{\partial P_{c2}}{\partial \delta\xi} = \frac{\partial e}{\partial P_{c2}}\frac{\partial TP_{c1}}{\partial \delta\xi}\tag{3} ∂δξ∂e=∂Pc2∂e∂δξ∂Pc2=∂Pc2∂e∂δξ∂TPc1(3)
接下里李群与李代数的结论就其作用了,
∂
T
P
c
1
∂
ξ
\frac{\partial TP_{c1}}{\partial \xi}
∂ξ∂TPc1的结果不就是李群与李代数最终的结论吗
∂
T
P
c
1
∂
δ
ξ
=
(
I
−
(
P
c
2
)
∧
0
T
0
T
)
=
(
1
1
1
0
−
Z
c
2
Y
c
2
1
1
1
Z
c
2
0
X
c
2
1
1
1
−
Y
c
2
X
c
2
0
)
(4)
\frac{\partial TP_{c1}}{\partial\delta\xi} = \left(\begin{matrix}I&-(P_{c2})^{\wedge}\\0^ T&0^T\end{matrix}\right)\\=\left(\begin{matrix}1&1&1&0&-Z_{c2}&Y_{c2}\\1&1&1&Z_{c2}&0&X_{c2}\\1&1&1&-Y_{c2}&X_{c2}&0\end{matrix}\right)\tag{4}
∂δξ∂TPc1=(I0T−(Pc2)∧0T)=
1111111110Zc2−Yc2−Zc20Xc2Yc2Xc20
(4)
假设 a a a表示一个向量,那么 a ∧ a^{\wedge} a∧就是 a a a的反对称矩阵
a ∧ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] (5) a^{\wedge} = \left[\begin{matrix} 0&-a_3&a_2\\a_3 &0&-a_1\\-a_2&a_1&0 \end{matrix} \right]\tag{5} a∧= 0a3−a2−a30a1a2−a10 (5)
那么 ∂ e ∂ P c 2 \frac{\partial e}{\partial P_{c2}} ∂Pc2∂e怎么求解呢:
首先我们把(2)展开,熟悉相机模型的展开应该很容易
(
e
u
e
v
)
=
(
u
2
v
2
)
−
1
z
c
2
(
f
x
0
c
y
0
f
y
c
x
0
0
1
)
(
x
c
2
y
c
2
z
c
2
)
=
(
u
2
−
f
x
X
c
2
Z
c
2
+
c
y
v
2
−
f
y
Y
c
2
Z
c
2
+
c
x
)
(6)
\left(\begin{matrix} e_u\\e_v\end{matrix}\right) = \left(\begin{matrix} u_2\\v_2\end{matrix}\right)-\frac{1}{z_{c2}}\left(\begin{matrix} f_x&0&c_y\\0&f_y&c_x\\0&0&1\end{matrix}\right)\left(\begin{matrix} x_{c2}\\y_{c2}\\z_{c2}\end{matrix}\right)=\left(\begin{matrix}u_2 -\frac{f_xX_{c2}}{Z_{c2}}+c_y\\v_2 -\frac{f_yY_{c2}}{Z_{c2}}+c_x\end{matrix}\right)\tag{6}
(euev)=(u2v2)−zc21
fx000fy0cycx1
xc2yc2zc2
=(u2−Zc2fxXc2+cyv2−Zc2fyYc2+cx)(6)
∂ e ∂ P c 2 = ( ∂ e u ∂ X c 2 ∂ e u ∂ Y c 2 ∂ e u ∂ Z c 2 ∂ e v ∂ X c 2 ∂ e v ∂ Y c 2 ∂ e v ∂ Z c 2 ) = − ( f x Z c 2 0 − f x X c 2 Z c 2 2 0 f y Z c 2 − f y Z c 2 2 Y c 2 ) (7) \frac{\partial e}{\partial P_{c2}}= \left(\begin{matrix} \frac{\partial e_u}{\partial X_{c2}}&\frac{\partial e_u}{\partial Y_{c2}}&\frac{\partial e_u}{\partial Z_{c2}}\\\frac{\partial e_v}{\partial X_{c2}}&\frac{\partial e_v}{\partial Y_{c2}}&\frac{\partial e_v}{\partial Z_{c2}} \end{matrix}\right)=-\left(\begin{matrix} \frac{f_x}{Z_{c2}}&0&-\frac{f_xX_{c2}}{Z_{c2}^2}\\0&\frac{f_y}{Z_{c2}}&-\frac{f_y}{Z_{c2}^2Y_{c2}}\end{matrix}\right) \tag{7} ∂Pc2∂e=(∂Xc2∂eu∂Xc2∂ev∂Yc2∂eu∂Yc2∂ev∂Zc2∂eu∂Zc2∂ev)=−(Zc2fx00Zc2fy−Zc22fxXc2−Zc22Yc2fy)(7)
将(4)(7)相乘可以得到最终的求导结果:
J
∂
ξ
=
∂
e
∂
δ
ξ
=
−
[
f
x
z
c
2
0
−
f
x
x
c
2
z
c
2
2
−
f
x
x
c
2
y
c
2
z
c
2
2
f
x
+
f
x
x
c
2
2
z
c
2
2
−
f
x
y
c
2
z
c
2
2
0
f
y
z
c
2
−
f
y
y
c
2
z
c
2
2
−
f
y
−
f
y
y
c
2
2
z
c
2
2
f
y
x
c
2
y
c
2
z
c
2
2
f
y
x
c
2
z
c
2
]
(8)
J_{\partial \xi} = \frac{\partial e}{ \partial \delta \xi} = -\left[\begin{matrix} \frac{f_x}{z_{c2}}&0&-\frac{f_xx_{c2}}{z_{c2}^2}&-\frac{f_xx_{c2}y_{c2}}{z_{c2}^2}&f_x+\frac{f_xx_{c2}^2}{z_{c2}^2}&-\frac{f_xy_{c2}}{z_{c2}^2}\\0&\frac{f_y}{z_{c2}}&-\frac{f_yy_{c2}}{z_{c2}^2}&-f_y-\frac{f_yy_{c2}^2}{z_{c2}^2}&\frac{f_yx_{c2}y_{c2}}{z_{c2}^2}&\frac{f_yx_{c2}}{z_{c2}}\end{matrix}\right]\tag{8}
J∂ξ=∂δξ∂e=−
zc2fx00zc2fy−zc22fxxc2−zc22fyyc2−zc22fxxc2yc2−fy−zc22fyyc22fx+zc22fxxc22zc22fyxc2yc2−zc22fxyc2zc2fyxc2
(8)
3.1.2. 误差对路标点求导
观察(7)式,(7)式是误差对特征点的相机坐标
P
c
2
P_{c2}
Pc2,现在要求是对误差对路标点求导,也就是
∂
e
∂
P
w
=
∂
e
∂
P
c
2
∂
P
c
2
∂
P
w
(9)
\frac{\partial e}{\partial P_{w}} = \frac{\partial e}{\partial P_{c2}} \frac{\partial P_{c2}}{\partial P_{w}} \tag{9}
∂Pw∂e=∂Pc2∂e∂Pw∂Pc2(9)
特征点在世界坐标系下和相机坐标系下的坐标转换如下:
P
c
2
=
e
x
p
(
ξ
∧
)
P
w
=
R
P
w
+
t
(10)
P_{c2} = exp(\xi \wedge)P_{w} = RP_{w}+t \tag{10}
Pc2=exp(ξ∧)Pw=RPw+t(10)
其中:
- R R R`:相机和世界坐标系下特征点之间的旋转矩阵
-
t
t
t:相机和世界坐标系下特征点之间的平移矩阵
todo这里的R和t真的是这个意思吗,那么这个R怎么求?pnp?
结合(7)(9)(10)可以得到误差对路标点求导
J
P
w
=
∂
e
∂
P
w
=
−
(
f
x
Z
c
2
0
−
f
x
X
c
2
Z
c
2
2
0
f
y
Z
c
2
−
f
y
Z
c
2
2
Y
c
2
)
R
(11)
J_{P_{w}}=\frac{\partial e}{\partial P_{w}} = -\left(\begin{matrix} \frac{f_x}{Z_{c2}}&0&-\frac{f_xX_{c2}}{Z_{c2}^2}\\0&\frac{f_y}{Z_{c2}}&-\frac{f_y}{Z_{c2}^2Y_{c2}}\end{matrix}\right)R\tag{11}
JPw=∂Pw∂e=−(Zc2fx00Zc2fy−Zc22fxXc2−Zc22Yc2fy)R(11)
4. BA的求解
4.1. 误差函数的构建
首先将待优化的相机位姿和路标点用变量
x
x
x来表示:
x
=
(
ξ
1
,
.
.
.
ξ
m
,
p
1
,
.
.
.
,
p
n
)
(12)
x = \left(\begin{matrix} \xi_1,...\xi_m,p_1,...,p_n \end{matrix}\right)\tag{12}
x=(ξ1,...ξm,p1,...,pn)(12)
Δ
x
=
(
Δ
ξ
1
,
.
.
.
Δ
ξ
m
,
Δ
p
1
,
.
.
.
,
Δ
p
n
)
(13)
\Delta x = \left(\begin{matrix} \ \Delta \xi_1,...\Delta \xi_m,\Delta p_1,...,\Delta p_n \end{matrix}\right)\tag{13}
Δx=( Δξ1,...Δξm,Δp1,...,Δpn)(13)
接着我们构建 e ( x + Δ x ) e(x+\Delta x) e(x+Δx)。它的意义是:根据非线性优化的思想,我们应该从某个初值开始,不断地寻找下降方向 Δ x \Delta x Δx来找到目标函数的最优解,不断地求解增量方程中的增量 Δ x \Delta x Δx。即找到一个 Δ ξ m \Delta \xi_m Δξm让每一个 ξ m + Δ ξ m \xi_m + \Delta \xi_m ξm+Δξm所对应的重投影误差最小;找到一个 Δ P w \Delta P_w ΔPw让每一个 P w + Δ P w P_w + \Delta P_w Pw+ΔPw所对应的重投影误差最小
误差函数
e
(
x
+
Δ
x
)
e(x+\Delta x)
e(x+Δx)是非线性函数,现在将其线性近似:
e
(
x
+
Δ
x
)
=
e
(
x
)
+
J
∂
ξ
Δ
ξ
+
J
P
w
Δ
p
(14)
e(x+\Delta x) = e(x)+J_{\partial \xi}\Delta\xi+J_{P_w}\Delta p\tag{14}
e(x+Δx)=e(x)+J∂ξΔξ+JPwΔp(14)
当然BA优化考虑的不是单一的位姿点和路标点,而是m个位姿和n个空间坐标,即对(14)求和。
所以这里重新定义误差函数:
∥
f
(
x
+
Δ
x
)
∥
=
1
2
∑
i
=
1
m
∑
j
=
1
n
∥
e
(
x
)
+
J
∂
ξ
i
j
Δ
ξ
i
j
+
J
P
w
i
j
Δ
p
∥
2
(15)
\|f(x+\Delta x)\| = \frac{1}{2}\sum \limits _{i=1} ^{m}\sum \limits _{j=1} ^{n}\|e(x)+J_{\partial \xi}^{ij} \Delta\xi_{ij}+J_{P_w}^{ij}\Delta p\|^2 \tag{15}
∥f(x+Δx)∥=21i=1∑mj=1∑n∥e(x)+J∂ξijΔξij+JPwijΔp∥2(15)
为了简化计算,现在定义:
E
=
∑
i
=
1
m
J
∂
ξ
i
j
(16)
E = \sum \limits _{i=1} ^{m}J_{\partial \xi}^{ij} \tag{16}
E=i=1∑mJ∂ξij(16)
F
=
∑
j
=
1
n
J
P
w
i
j
(17)
F = \sum \limits _{j=1} ^{n}J_{P_w}^{ij} \tag{17}
F=j=1∑nJPwij(17)
J
=
(
E
F
)
(18)
J = \left(\begin{matrix}E&F\end{matrix}\right)\tag{18}
J=(EF)(18)
那么误差函数可以修改为
∥
f
(
x
+
Δ
x
)
∥
=
1
2
∥
e
(
x
)
+
J
Δ
x
∥
2
(19)
\|f(x+\Delta x)\| = \frac{1}{2}\|e(x)+J\Delta x\|^2 \tag{19}
∥f(x+Δx)∥=21∥e(x)+JΔx∥2(19)
4.2. 非线性优化(G-N法)
对(19)式进行展开得到:
f
(
x
+
Δ
x
)
=
1
2
∥
e
(
x
)
2
+
2
e
(
x
)
J
Δ
x
+
Δ
x
T
J
J
T
Δ
x
∥
(20)
f(x+\Delta x) = \frac{1}{2}\|e(x)^2+2e(x)J\Delta x+\Delta x^TJJ^T\Delta x\|\tag{20}
f(x+Δx)=21∥e(x)2+2e(x)JΔx+ΔxTJJTΔx∥(20)
对(20)式进行求导得到并令其等于0,得到误差函数的梯度:
∂
f
(
x
+
Δ
x
)
∂
Δ
x
=
1
2
∥
2
e
(
x
)
J
+
2
J
J
T
Δ
x
∥
=
0
(21)
\frac{\partial f(x+\Delta x)}{\partial\Delta x} = \frac{1}{2}\|2e(x)J+2JJ^T\Delta x\| = 0\tag{21}
∂Δx∂f(x+Δx)=21∥2e(x)J+2JJTΔx∥=0(21)
e ( x ) J + J J T Δ x = 0 (22) e(x)J+JJ^T\Delta x = 0\tag{22} e(x)J+JJTΔx=0(22)
J
J
T
Δ
x
=
−
e
(
x
)
J
(23)
JJ^T\Delta x = -e(x)J\tag{23}
JJTΔx=−e(x)J(23)
令
H
=
J
J
T
(24)
H = JJ^T\tag{24}
H=JJT(24)
g
=
−
e
(
x
)
J
(25)
g = -e(x)J\tag{25}
g=−e(x)J(25)
所以误差函数的梯度就为:
Δ
x
=
−
H
−
1
g
(26)
\Delta x = -H^{-1}g\tag{26}
Δx=−H−1g(26)
这时只需要根据(26)多轮迭代更新计算梯度就可以得到让误差函数 f ( x + Δ x ) f(x+\Delta x) f(x+Δx)最小的最优解。
5. 稀疏矩阵
观察(24)式, H H H矩阵是一个高维矩阵,它的维数就是此时优化窗口的帧数,非常大,求逆非常复杂。
若有10个相机同时看到100个路标点,BA雅各比矩阵有多少维?
SLAM中相机姿态用李代数(SE3)表示, SE3是6维的,路边点的位置是三维的(X,Y,Z),因此状态矩阵的维度是1x(10x6+100x3)
一个路标点的误差的维度为2,误差即为实际像素坐标 ( u ^ , v ^ ) (\hat{u},\hat{v}) (u^,v^)与观测的路标点的像素 ( u , v ) (u,v) (u,v)之间的误差。一个相机中100个点的误差维度为200,5个相机5x200。
所以雅克比矩阵的维度即为误差矩阵维度x状态矩阵维度
对(18)式进行展开
J
=
(
0
,
.
.
.
,
0
,
∂
e
∂
ξ
i
,
.
.
.
0
,
0
,
∂
e
∂
P
w
i
,
0...
,
0
)
(27)
J = (0,...,0,\frac{\partial e}{\partial \xi_i},...0,0,\frac{\partial e}{\partial P_w^i},0...,0)\tag{27}
J=(0,...,0,∂ξi∂e,...0,0,∂Pwi∂e,0...,0)(27)
可以看到
J
J
J只跟当前帧的位姿和路标点有关,为稀疏矩阵,对稀疏矩阵特殊处理可以优化计算过程
通过(24)式可以观察到单应矩阵
H
H
H是一个矩阵的转置乘于该矩阵得到的结果
现在令
H
=
[
B
E
E
T
C
]
(28)
H = \begin{bmatrix}B&E\\E^T&C\end{bmatrix}\tag{28}
H=[BETEC](28)
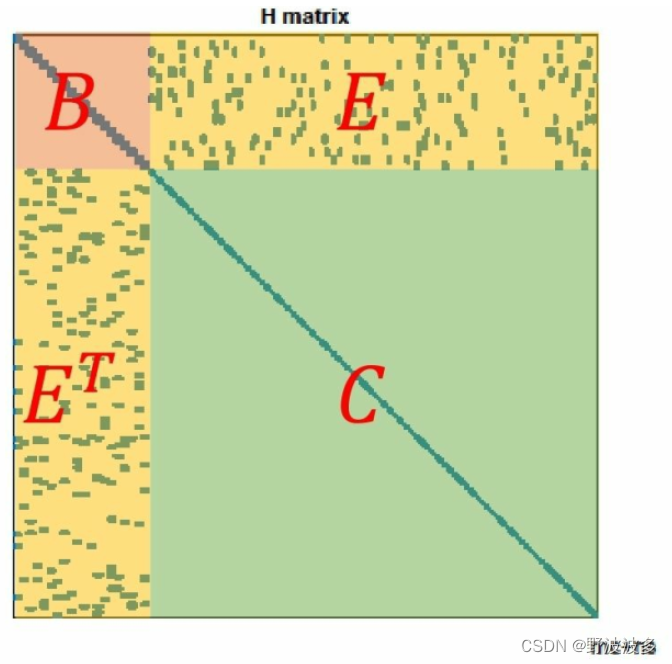
B
B
B:对角块矩阵,每个对角块的维度和相机参数的维度相同(6x6),对角块的个数是相机变量的个数。
C
C
C:对角块矩阵,每个对角块的维度和路标参数的维度相同(3x3),对角块的个数是路标变量的个数(非常多)。
如果直接对
H
H
H求逆会非常复杂,这里利用舒尔补对
H
Δ
x
=
g
H\Delta x = g
HΔx=g进行处理:
[
I
−
E
C
−
1
0
1
]
[
B
E
E
T
C
]
[
Δ
x
c
Δ
x
p
]
=
[
I
−
E
C
−
1
0
1
]
[
v
w
]
(29)
\begin{bmatrix}I&-EC^{-1}\\0&1\end{bmatrix}\begin{bmatrix}B&E\\E^T&C\end{bmatrix}\begin{bmatrix}\Delta x_c\\\Delta x_p\end{bmatrix} =\begin{bmatrix}I&-EC^{-1}\\0&1\end{bmatrix}\begin{bmatrix}v\\w\end{bmatrix} \tag{29}
[I0−EC−11][BETEC][ΔxcΔxp]=[I0−EC−11][vw](29)
整理得到
[
B
−
E
C
−
1
E
T
]
Δ
x
c
=
v
−
E
C
−
1
w
(30)
[B-EC^{-1}E^T]\Delta x_c = v-EC^{-1}w\tag{30}
[B−EC−1ET]Δxc=v−EC−1w(30)
Δ
x
p
=
C
−
1
(
w
−
E
T
Δ
x
c
)
(31)
\Delta x_p = C^{-1}(w-E^T\Delta x_c)\tag{31}
Δxp=C−1(w−ETΔxc)(31)
因为C是对角块矩阵,所以 C − 1 C^{-1} C−1非常容易求得,(30)(31)就避免了直接求解 H − 1 H^{-1} H−1的难题。
6. Eigen库构建雅克比矩阵
#include <iostream>
#include <vector>
#include <random>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>
struct Pose
{
Pose(Eigen::Matrix3d R, Eigen::Vector3d t):Rwc(R),qwc(R),twc(t) {};
Eigen::Matrix3d Rwc;
Eigen::Quaterniond qwc;
Eigen::Vector3d twc;
};
int main()
{
int featureNums = 20;
int poseNums = 10;
int diem = poseNums * 6 + featureNums * 3;
double fx = 1.;
double fy = 1.;
Eigen::MatrixXd H(diem,diem);
H.setZero();
std::vector<Pose> camera_pose;
double radius = 8;
for(int n = 0; n < poseNums; ++n ) {
double theta = n * 2 * M_PI / ( poseNums * 4); // 1/4 圆弧
// 绕 z轴 旋转
Eigen::Matrix3d R;
R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());
Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));
camera_pose.push_back(Pose(R,t));
}
// 随机数生成三维特征点
std::default_random_engine generator;
std::vector<Eigen::Vector3d> points;
for(int j = 0; j < featureNums; ++j)
{
std::uniform_real_distribution<double> xy_rand(-4, 4.0);
std::uniform_real_distribution<double> z_rand(8., 10.);
double tx = xy_rand(generator);
double ty = xy_rand(generator);
double tz = z_rand(generator);
Eigen::Vector3d Pw(tx, ty, tz);
points.push_back(Pw);
for (int i = 0; i < poseNums; ++i) {
Eigen::Matrix3d Rcw = camera_pose[i].Rwc.transpose();
Eigen::Vector3d Pc = Rcw * (Pw - camera_pose[i].twc);
double x = Pc.x();
double y = Pc.y();
double z = Pc.z();
double z_2 = z * z;
Eigen::Matrix<double,2,3> jacobian_uv_Pc;
jacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,
0, fy/z, -y * fy/z_2;
Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw;
Eigen::Matrix<double,2,6> jacobian_Ti;
jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,
-(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2;
H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;
H.block(j * 3 + 6 * poseNums, j * 3 + 6 * poseNums, 3, 3) += jacobian_Pj.transpose() * jacobian_Pj;
H.block(i * 6, j * 3 + 6 * poseNums, 6, 3) += jacobian_Ti.transpose() * jacobian_Pj;
H.block(j*3 + 6*poseNums,i*6 , 3,6) += jacobian_Pj.transpose() * jacobian_Ti;
}
}
}





















 9461
9461

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








