目录
一、各种系统
1、因果系统
输出不发生在输入之前,即n<0时 h(n)=0
(1)线性时不变系统是因果系统的充要条件
(2)因果系统收敛域在某圆外侧
2、稳定系统
有界输入产生有界输出,即 n=-∞+∞hn<∞![]() (充分必要条件)
(充分必要条件)
3、有记忆系统&无记忆系统
有记忆系统:系统中具有保留或储存不是当前时刻输入信息的功能。
无记忆系统:对于自变量得每一个值,一个系统的输出仅仅取决于该时刻得输入。
4、线性系统
线性系统(连续时间或离散时间)具有的一种重要性质就是叠加性质。即如果一个输入由几个信号的加权和组成,那么输出也就是系统对这组信号中每一个的响应的加权和。
![]()
5、时不变系统(移不变系统)
若系统的特性和行为不随时间而变,该系统就是时不变的。如果再输入信号上有一个时移,而在输出信号中产生同样的时移,那么这个系统就是时不变的,确认系统是时不变,需要判定对于任何输入与任何时移 t0时不变性。
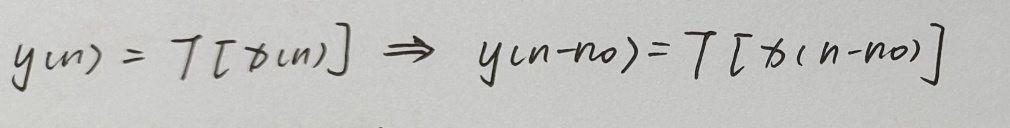
二、收敛域与因果性的关系
 z变换大家肯定都知道,最终不要的一点在z变换的定义中,除了表达式外,还要指定收敛域。z变换的定义为
z变换大家肯定都知道,最终不要的一点在z变换的定义中,除了表达式外,还要指定收敛域。z变换的定义为
收敛域是使X(z)的值为有限的所有z值的集合,所以收敛域肯定不包含极点,是极点之外的地方。
结论一:因果信号的收敛域是某个半径r的圆的外部;
非因果信号的收敛域是某个半径r的内部。
举个例题——因果系统

非因果系统:

双变系统分情况讨论:

三、收敛域与稳定性的关系

记住一点:
如果线性不变系统是稳定的,那么单位圆包含于H(z)的收敛域内
总结:线性时不变因果稳定系统的极点都在单位圆内
单位圆上的z变换就是傅里叶变换
四、零极点和频率响应的关系
在说零极点和频率响应的关系前,我必须提一下z变换的z域和拉普拉斯变换的s域的关系,因为看频率响应的话,都是转换到s域来看。s平面的左半平面映射到z平面的单位圆内;s平面的右半平面映射到单位圆外部;s平面的jw轴映射到z平面的单位圆。因此,线性时不变因果稳定的系统,其极点都在s平面的左半平面。
五、最小相位系统
1、什么是最小相位系统?
![]()
2、FIR、IIR的最小相位系统
FIR(无极点):如果系统函数的所有零点都位于单位圆内,则称该系统为最小相位系统;如果系统函数的所有零点都位于单位圆外,则称该系统为最大相位系统;如果一部分零点位于单位圆内,一部分零点位于单位圆外,则称该系统为混合相位系统或非最小相位系统。
IIR(有极点):如果系统函数的所有零点和极点都在单位圆内,则称该系统为最小相位系统。
3、特点
- 最小相位系统是因果且稳定的;
- 其逆系统也是因果且稳定的;
- 在所有具有相同幅频响应的零-极点系统中,最小相位系统的群时延最小。
六、全通系统
1、什么是全通系统?
顾名思义,全通系统通俗点讲就是能让所有信号通过的系统,所以这就要求:

2、全通系统极零点分布的显著特点
每一个极点都对应一个互为共轭倒数零点
3、性质
群时延具有正值性以及连续相位具有非正值性!所以在实际应用中,全通系统可以作为相位失真的补偿!








 本文详细探讨了IT技术中的各种系统,包括因果性、稳定性、有记忆与无记忆系统、线性系统特性、时不变系统、收敛域与因果性和稳定性的关系、零极点与频率响应、最小相位系统定义及其特点,以及全通系统的概念和性质。
本文详细探讨了IT技术中的各种系统,包括因果性、稳定性、有记忆与无记忆系统、线性系统特性、时不变系统、收敛域与因果性和稳定性的关系、零极点与频率响应、最小相位系统定义及其特点,以及全通系统的概念和性质。

















 837
837

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










