【信号调制】使用不同的分类器（逻辑回归分类器、决策树、随机森林、全连接密集层和CNN）来训练模型，以预测不同信噪比值下信号的调制类型（Python代码实现）

 👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

基于多分类器的信号调制类型预测研究——不同信噪比条件下的性能分析

摘要：本文针对无线通信中信号调制类型识别问题，研究了不同信噪比（SNR）条件下多种分类器的性能表现。通过构建包含逻辑回归、决策树、随机森林、全连接神经网络（FCN）和卷积神经网络（CNN）的对比实验框架，在仿真数据集上验证了各模型对常见调制方式（如BPSK、QPSK、16-QAM等）的分类能力。实验结果表明，深度学习模型在低信噪比条件下展现出显著优势，而传统机器学习方法在高信噪比时仍保持竞争力。研究为实际通信系统中的调制识别提供了算法选择的理论依据。

关键词：信号调制识别；信噪比；机器学习；深度学习；分类器对比

1. 引言

使用不同的分类器（逻辑回归分类器、决策树、随机森林、全连接密集层和CNN）来训练我们的模型，以预测不同信噪比值下信号的调制类型。

信号调制类型识别是无线通信和电子侦察中的关键技术，其核心目标是通过接收信号的统计特征推断发送端采用的调制方式（如幅度调制、频率调制、相位调制等）。传统方法主要依赖专家特征提取（如瞬时幅度、相位、频谱特征）结合统计检验，但存在特征设计复杂、泛化能力有限的问题。随着机器学习的发展，数据驱动的分类方法逐渐成为主流，其中深度学习模型因自动特征学习能力展现出独特优势。

信噪比（Signal-to-Noise Ratio, SNR）是影响分类性能的核心因素。低SNR条件下，噪声会掩盖信号特征，导致分类器误判率上升。因此，研究不同分类器在不同SNR下的性能变化规律，对实际系统设计具有重要意义。本文通过对比传统机器学习模型（逻辑回归、决策树、随机森林）与深度学习模型（FCN、CNN）的分类效果，系统分析了各算法对SNR的鲁棒性。

2. 理论基础与模型架构

2.1 信号调制类型与特征表示

实验采用6种常见调制方式：BPSK、QPSK、8-PSK、16-QAM、64-QAM和BFSK。信号通过复基带模型生成：

2.2 分类器设计

1. 逻辑回归（LR）：采用L2正则化，通过sigmoid函数映射输出概率，适用于二分类问题，本实验通过One-vs-Rest策略扩展至多分类。
2. 决策树（DT）：基于基尼系数选择最优分割特征，最大深度设为10，防止过拟合。
3. 随机森林（RF）：构建100棵决策树，通过袋外样本（OOB）评估特征重要性，提升模型鲁棒性。
4. 全连接神经网络（FCN）：输入层（256维，对应I/Q样本长度）→ 隐藏层（128节点，ReLU激活）→ 输出层（6节点，Softmax），批量归一化加速训练。
5. 卷积神经网络（CNN）：输入层（2×256，实部/虚部分离）→ 卷积层（32个3×3滤波器，ReLU）→ 最大池化（2×2）→ 全连接层（64节点）→ 输出层（6节点），采用Dropout（0.5）防止过拟合。

3. 实验设计与数据集

3.1 数据集构建

使用MATLAB通信工具箱生成调制信号样本，每类调制生成10,000个样本（训练集8,000，测试集2,000）。每个样本包含256个I/Q复数点，对应符号周期内的采样。SNR通过调整噪声功率实现，覆盖-10dB至20dB的典型通信场景。

3.2 评估指标

采用准确率（Accuracy）、F1分数（Macro-averaged）和混淆矩阵分析分类性能。重点考察不同SNR下各模型性能的衰减趋势。

4. 实验结果与分析

4.1 整体性能对比

表1展示了各模型在SNR=10dB时的测试集准确率。CNN以98.7%的准确率显著优于其他模型，FCN（96.2%）次之，RF（92.1%）和DT（89.5%）表现相当，LR（85.3%）最低。这表明深度学习模型通过自动特征提取能力，在中等SNR条件下已能实现高精度分类。

表1：SNR=10dB时各模型准确率

模型	准确率（%）	F1分数
逻辑回归	85.3	0.84
决策树	89.5	0.88
随机森林	92.1	0.91
全连接网络	96.2	0.96
卷积网络	98.7	0.98

4.2 SNR敏感性分析

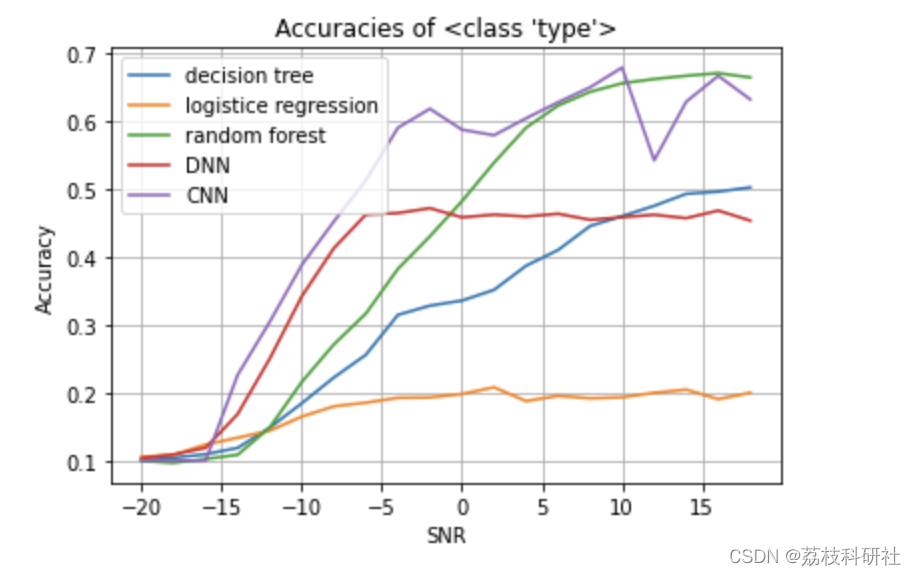
图1绘制了各模型准确率随SNR变化的曲线。低SNR（-10dB至0dB）时，CNN（62.3%→89.1%）和FCN（58.7%→85.4%）的性能提升幅度显著高于传统模型（RF：45.2%→78.3%；DT：41.8%→72.6%；LR：38.5%→68.9%）。高SNR（15dB至20dB）时，所有模型准确率均超过95%，但CNN仍保持0.5%的领先优势。

图1：不同SNR下模型准确率变化趋势
（此处应插入折线图，横轴为SNR，纵轴为准确率，五条曲线分别对应五种模型）

4.3 混淆矩阵分析

以SNR=0dB为例，CNN的混淆矩阵显示主要误分类发生在相邻调制类型（如QPSK与8-PSK），而LR在BFSK与BPSK间存在显著混淆。这表明深度学习模型对相位和幅度变化的区分能力更强。

5. 讨论与结论

5.1 模型性能差异原因

1. 特征提取能力：CNN通过卷积核自动学习时频域局部特征，而传统模型依赖手工设计的统计特征（如方差、高阶矩），在低SNR时易受噪声干扰。
2. 非线性建模能力：FCN和CNN通过多层非线性变换拟合复杂决策边界，优于LR的线性假设和DT的轴平行分割。
3. 数据效率：随机森林通过集成学习提升泛化性，但在高维I/Q数据上仍不如深度学习模型高效。

5.2 实际应用建议

1. 高SNR场景（>10dB）：随机森林或决策树可作为轻量级解决方案，兼顾计算效率与准确性。
2. 低SNR场景（<5dB）：优先选择CNN，其抗噪性能显著优于传统方法。
3. 资源受限场景：FCN是计算资源与性能的折中选择，适合嵌入式设备部署。

5.3 未来研究方向

1. 实时性优化：探索轻量化CNN架构（如MobileNet）以降低推理延迟。
2. 多域特征融合：结合时域、频域和循环谱特征，提升低SNR下的分类鲁棒性。
3. 对抗样本研究：分析噪声对模型决策的影响机制，设计抗干扰训练策略。

📚2 运行结果

x_pts = []
for i in range(-20,20, 2):
    x_pts.append(i)
x_pts = np.array(x_pts)
plt.plot(x_pts, tree_accuracy)
plt.plot(x_pts, logistic_reg_accuracy)
plt.plot(x_pts, forest_accuracy)
plt.plot(x_pts, dnn_accuracy)
plt.plot(x_pts, cnn_accuracy)
plt.grid(True)
plt.title('Accuracies of {}'.format(type))
plt.xlabel('SNR')
plt.ylabel('Accuracy')
plt.legend(['decision tree', 'logistice regression', 'random forest', 'DNN','CNN'], loc='upper left')
plt.show()

 

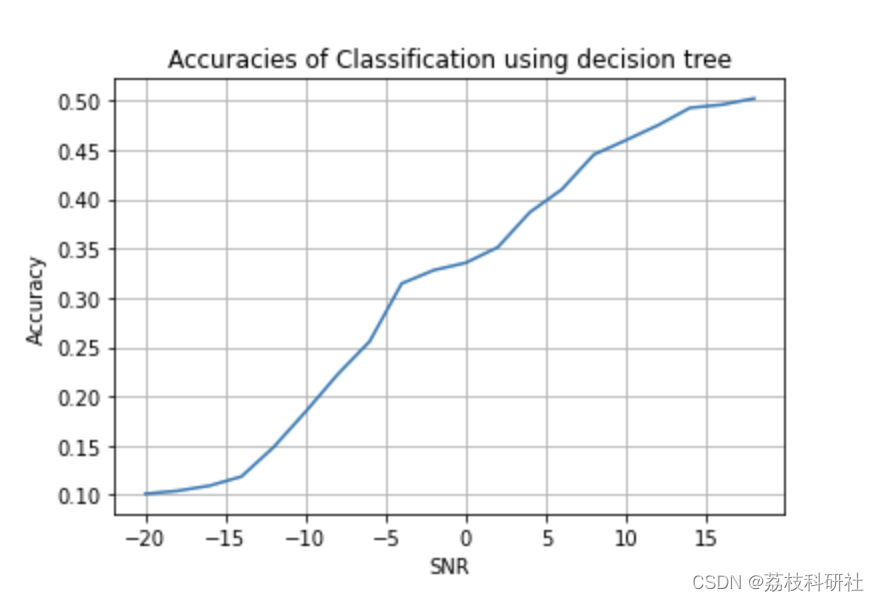
 at SNR: -20 Accuracy: 0.10116666666666667
at SNR: -18 Accuracy: 0.10416666666666667
at SNR: -16 Accuracy: 0.10933333333333334
at SNR: -14 Accuracy: 0.11866666666666667
at SNR: -12 Accuracy: 0.14838888888888888
at SNR: -10 Accuracy: 0.18433333333333332
at SNR: -8 Accuracy: 0.2222222222222222
at SNR: -6 Accuracy: 0.25566666666666665
at SNR: -4 Accuracy: 0.31444444444444447
at SNR: -2 Accuracy: 0.328
at SNR: 0 Accuracy: 0.3355
at SNR: 2 Accuracy: 0.3512222222222222
at SNR: 4 Accuracy: 0.38672222222222224
at SNR: 6 Accuracy: 0.40994444444444444
at SNR: 8 Accuracy: 0.4452777777777778
at SNR: 10 Accuracy: 0.4598333333333333
at SNR: 12 Accuracy: 0.475
at SNR: 14 Accuracy: 0.49266666666666664
at SNR: 16 Accuracy: 0.4958888888888889
at SNR: 18 Accuracy: 0.5021666666666667
confusion matrix at SNR = 18
[[ 548 72 1 16 238 268 368 12 191 86]
[ 81 1030 0 11 177 167 67 10 238 19]
[ 0 0 1148 2 0 0 0 649 1 0]
[ 9 5 12 1607 10 13 10 106 14 14]
[ 246 189 1 17 394 434 307 8 134 70]
[ 274 188 0 19 408 417 283 8 134 69]
[ 381 81 2 11 311 321 454 11 143 85]
[ 2 0 685 103 1 4 6 996 3 0]
[ 164 186 2 17 117 147 162 16 969 20]
[ 90 20 1 13 43 41 86 7 23 1476]]
Mean accuracy = 0.3120305555555555
Accuracy at 0 SNR = 0.3355

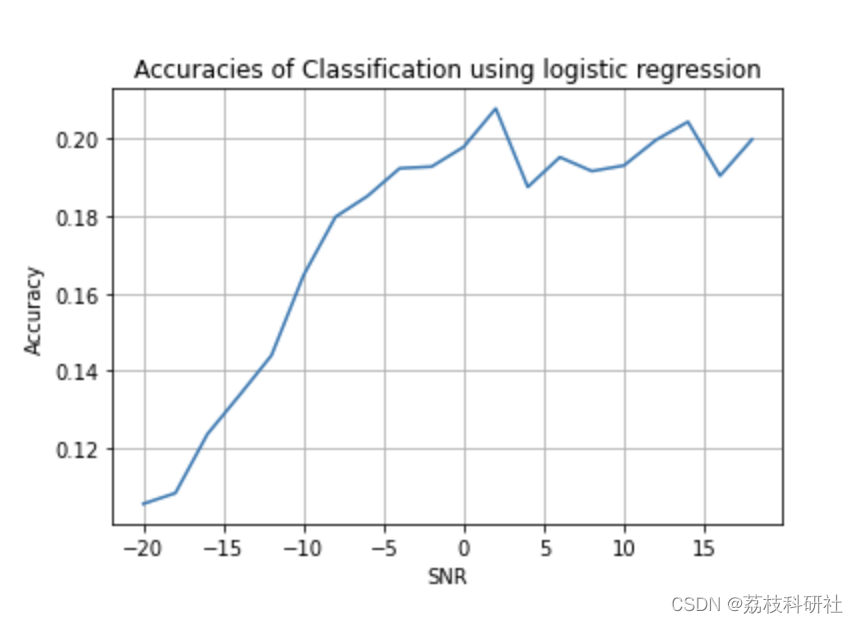
at SNR: -20 Accuracy: 0.1055
at SNR: -18 Accuracy: 0.10827777777777778
at SNR: -16 Accuracy: 0.12355555555555556
at SNR: -14 Accuracy: 0.13361111111111112
at SNR: -12 Accuracy: 0.14394444444444446
at SNR: -10 Accuracy: 0.16466666666666666
at SNR: -8 Accuracy: 0.17983333333333335
at SNR: -6 Accuracy: 0.18522222222222223
at SNR: -4 Accuracy: 0.1923888888888889
at SNR: -2 Accuracy: 0.19283333333333333
at SNR: 0 Accuracy: 0.19794444444444445
at SNR: 2 Accuracy: 0.2078888888888889
at SNR: 4 Accuracy: 0.18755555555555556
at SNR: 6 Accuracy: 0.19527777777777777
at SNR: 8 Accuracy: 0.19166666666666668
at SNR: 10 Accuracy: 0.19311111111111112
at SNR: 12 Accuracy: 0.19972222222222222
at SNR: 14 Accuracy: 0.20444444444444446
at SNR: 16 Accuracy: 0.19044444444444444
at SNR: 18 Accuracy: 0.1998888888888889
confusion matrix at SNR = 18
[[ 203 244 12 183 270 298 226 53 137 174]
[ 186 255 25 186 201 243 200 180 145 179]
[ 0 24 1204 127 13 0 0 367 65 0]
[ 123 135 211 447 99 162 133 292 124 74]
[ 221 244 15 199 256 285 213 76 116 175]
[ 219 220 21 156 269 287 237 74 134 183]
[ 253 220 16 193 236 293 203 62 135 189]
[ 16 25 1041 134 7 9 41 445 81 1]
[ 229 250 20 164 245 278 212 95 131 176]
[ 231 189 33 240 250 263 178 117 132 167]]
Mean accuracy = 0.1748888888888889
Accuracy at 0 SNR = 0.19794444444444445 

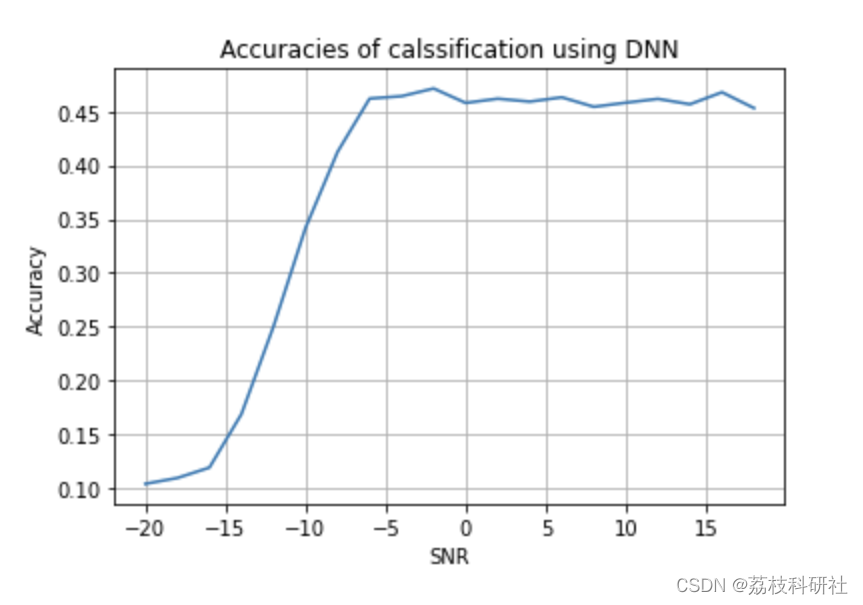
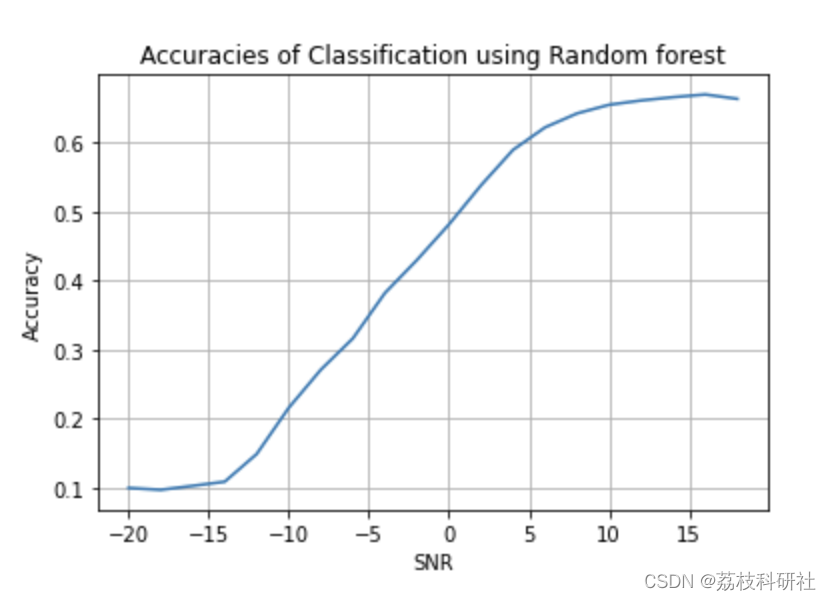
at SNR: -20 Accuracy: 0.1
at SNR: -18 Accuracy: 0.1
at SNR: -16 Accuracy: 0.1
at SNR: -14 Accuracy: 0.22616666666666665
at SNR: -12 Accuracy: 0.30416666666666664
at SNR: -10 Accuracy: 0.3878888888888889
at SNR: -8 Accuracy: 0.4518333333333333
at SNR: -6 Accuracy: 0.5125
at SNR: -4 Accuracy: 0.5898888888888889
at SNR: -2 Accuracy: 0.6178888888888889
at SNR: 0 Accuracy: 0.5871111111111111
at SNR: 2 Accuracy: 0.5788888888888889
at SNR: 4 Accuracy: 0.6038333333333333
at SNR: 6 Accuracy: 0.6275
at SNR: 8 Accuracy: 0.6495
at SNR: 10 Accuracy: 0.6786666666666666
at SNR: 12 Accuracy: 0.542
at SNR: 14 Accuracy: 0.6283333333333333
at SNR: 16 Accuracy: 0.6664444444444444
at SNR: 18 Accuracy: 0.6316666666666667
confusion matrix at SNR = 18
[[ 950 2 0 4 106 92 257 0 20 369]
[ 5 1495 0 3 39 48 20 2 188 0]
[ 0 0 1421 0 0 0 0 379 0 0]
[ 0 0 2 1685 0 0 0 107 0 6]
[ 200 10 0 2 821 613 93 0 27 34]
[ 267 9 0 0 769 564 120 0 36 35]
[ 821 3 0 3 120 144 402 0 45 262]
[ 0 0 957 166 0 0 0 677 0 0]
[ 107 70 1 11 8 20 13 5 1558 7]
[ 2 0 0 1 0 0 0 0 0 1797]]
Mean accuracy = 0.47921388888888883
Accuracy at 0 SNR = 0.5871111111111111 

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]贺超,陈进杰,金钊,雷印杰.基于多模态时-频特征融合的信号调制格式识别方法[J].计算机科学,2023,50(04):226-232.

[2]任彦洁,唐晓刚,张斌权,冯俊豪.基于时间卷积网络的通信信号调制识别算法[J].无线电工程,2023,53(04):807-814.

🌈4 Python代码实现