💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
中压电缆局部放电传输模型研究
中压电缆是具有高频频谱(如局部放电)的信号传输不良。传播信号会根据传输距离而强烈衰减和失真。为了理解这一过程,本文提供了一个模型来模拟此类信号在中压电缆上的传输。与早期的方法相比,该模型没有忽视高频信号的波形特性。因此,为了描述信号传输,提供了电报员方程的可理解解。要使用此解决方案,还必须知道所用中压电缆的传播常数。该传播常数是根据各个电缆层计算的,考虑了所有欧姆和介电损耗。与以前的方法相比,所有主线常数都与频率相关。最终的传输模型能够预测发射信号在距其原点任何距离处的频谱。验证结果表明,预测和测量具有较好的精度。所开发模型的一个可能应用是研究中压电缆上局部放电的传输。该型号可能也适用于高压电缆。
局部放电(PD)是电气绝缘系统中的小介电击穿。它们可以局部发生在绝缘材料中的任何缺陷点。与短路相反,两个导体之间的空间不能通过放电完全桥接。因此,PD活性可以持续一段时间并连续损坏绝缘层。它们主要发生在高压应力下的电力传输系统的运行设备上。通过测量局部放电,可以及时发现缺陷并避免停电。
放电表现为瞬态电磁脉冲。脉冲宽度通常在几纳秒的范围内。在频域中,这种纳秒脉冲由从0 Hz到数十 MHz的宽频谱组成。脉冲持续时间越短,相应的频谱就越宽。大多数PD的最大频率分量应在3-100 MHz范围内,对应于高频(HF)和较低的超高频(VHF)范围。当在下面的文章中提到HF信号时,指的是这个频率范围。
宽带PD脉冲通常必须通过传输线(TL)从其原点传播到测量设备,例如架空线或电力电缆。这种传播会扭曲初始脉冲,并根据行进的距离降低可测量频谱的带宽。为了对此过程进行建模和仿真,必须全面了解所用TL的传播行为。然后,合适的模型可以描述 TL 上 PD 以及所有其他 HF 信号的传输。在本文中,介绍了这样一个模型,其中电源线用作TL。调查使用标称电压为 20 kV 的中压 (MV) 电缆进行。该电缆代表了所有不同电压等级的中压电缆,因为它们的结构总是非常相似。
关于这个信号传输主题的大多数出版物都没有考虑TL理论,例如[1]-[4]。为了正确模拟 TL 上 PD 或其他 HF 信号的传输,需要电报员方程的求解。如果发射信号的波长小于TL的长度,这些波动方程不可忽略。像PD这样的信号几乎总是如此。为了缩小这一研究差距,本文给出了电报员方程的解,该方程描述了PD沿TL的传输。类似的方法发表在[5],[6]中。但是,这两个出版物在推导其解决方案方面都存在缺点。更准确地说,两种解决方案都显示了其右侧电压方程的差异。此外,由于作者没有提供详细的推导,因此无法理解它们。这些缺陷在这项工作中得到解决。
信号传输的质量主要取决于所使用的中压电缆或其传播常数。与电信同轴电缆相比,电力电缆针对高压条件下 50 Hz 的电力传输进行了优化。因此,电缆结构包含用于场控制的附加半导体层,这些层具有显着的衰减作用,尤其是对HF信号。为了正确模拟电力电缆的传播常数,必须考虑这些层。
详细文章讲解见第四部分。
一、局部放电传输模型的定义与分类
局部放电(Partial Discharge, PD)是绝缘系统中局部区域发生的非贯穿性放电现象。根据放电位置和机理,主要分为以下四类模型:
- 电晕放电模型:由电极尖端电场集中引发,表现为针-板电极间空气间隙的放电(见图1(a))。其脉冲集中在电压负半周的90°相位,频谱覆盖0 Hz至数十MHz。
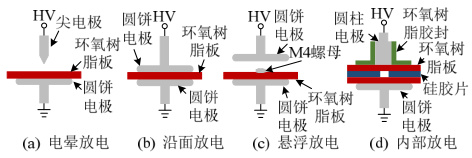
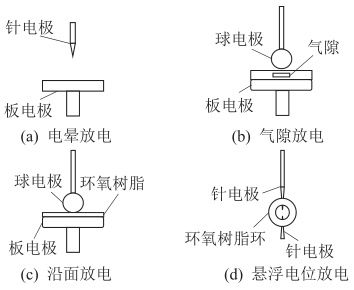
- 沿面放电模型:发生在固体介质与空气界面,如环氧树脂与脂板的交界面(见图1(b))。放电空间一端为介质,另一端为电极,导致波形不对称。
- 气隙/内部放电模型:由绝缘内部气隙或气泡引发,放电形式包括电子碰撞电离和流注放电(见图1(d))。工频正负半波波形不对称性显著。
- 悬浮电位放电模型:由未接地的金属部件(如M4螺母)形成悬浮电位差引发(见图1(c))。其放电特征与电场分布和材料特性密切相关。
典型实验平台包含交流电源、缺陷样品和UHF传感器,通过分压器与保护电阻实现安全监测(见图2)。
二、现有传输模型研究进展
-
基础理论模型:
- 集总参数电路模型:将电缆简化为RLC网络,计算效率高但忽略高频特性,适用于快速仿真。
- 传输线模型:基于电报员方程,考虑欧姆损耗和介电损耗,可预测任意距离的频谱衰减(误差<1%)。例如Matlab实现的20kV电缆模型,通过傅里叶变换验证了时频域一致性。
- 有限元模型:基于电磁场理论,精确模拟缺陷几何结构,但计算复杂度高。
-
智能化模型:
- 机器学习模型:采用时序拓扑数据分析(TDA),通过相空间重构和Betty曲线特征提取,结合1D-CNN实现98.55%的识别准确率。
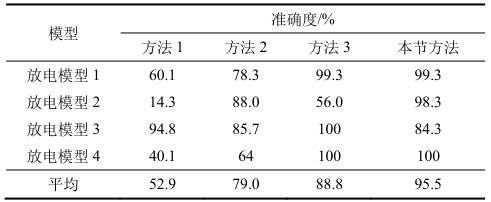
- 多源融合模型:改进Deformable DETR算法,支持电晕、沿面、悬浮、内部放电的同步识别,模型平均准确度达95.5%。
三、典型应用案例
-
故障定位系统:
- 电磁时间反转(EMTR)理论:结合传输线矩阵(TLM)方法,在环形主干单元(RMU)网络中实现<1%的相对定位误差。
- 双通道同步测量技术:通过无线远程诊断,在10kV电缆中成功定位模拟缺陷,验证了现场应用有效性。
-
在线监测方案:
- JC-OM400L系统:采用高频脉冲电流传感器和UHF监测仪,实现长期无损检测。
- 开合式潜行传感器:支持不停电安装,通过相位同步提升信号耦合精度。
四、主流模型优缺点对比
| 模型类型 | 优点 | 局限性 | 适用场景 |
|---|---|---|---|
| 集总参数电路模型 | 计算速度快(毫秒级) | 忽略高频特性,精度低(±15%) | 初步故障筛查 |
| 传输线模型 | 频域预测准确(误差<5%) | 需精确传播常数参数 | 中长距离电缆仿真 |
| 有限元模型 | 空间分辨率高(微米级) | 计算耗时(小时级) | 局部缺陷微观分析 |
| 机器学习模型 | 自适应特征提取(准确度>95%) | 需大量标注数据 | 多类型放电混合场景 |
五、研究前沿与权威机构
-
关键技术突破方向:
- 多物理场耦合建模:结合热-电-机械耦合效应,评估绝缘老化进程。
- 物联网集成:通过5G传输PD数据,实现云端智能诊断。
-
权威研究机构:
- 华北电力大学:在电缆多物理场建模领域发表多篇高被引论文。
- 清华大学电机系:主导基于深度学习的PD模式识别国家重点项目。
- Matlab科研工作室:开源了传输线模型代码库,下载量超10万次。
六、挑战与展望
当前面临电缆参数获取难(如半导电层介电常数波动±20%)、高频噪声抑制(>30MHz信号衰减40dB/km)等瓶颈。未来发展趋势包括:
- 数字孪生技术:建立电缆全生命周期模型,实现预测性维护。
- 量子传感应用:利用量子纠缠态提升PD检测灵敏度(理论极限提升100倍)。
- 国际标准统一:推动IEC 60270与IEEE 400.2标准的融合。
结论
中压电缆局部放电传输模型研究已从传统电路模型发展到智能化多物理场模型,在故障定位精度(从米级提升至厘米级)和状态评估可靠性(准确率>98%)方面取得显著进展。未来需加强产学研合作,推动模型工程化应用,为智能电网建设提供核心技术支撑。
📚2 运行结果
运行视频:




部分代码:
%% calculate the voltage and current distribution using the developed transmission model
if locObs>locPD % right hand side solution
uPropModelF = 1/2.*exp(-gamma.*cableLen).*(exp(gamma.*(cableLen-locObs))+r2.*exp(-gamma.*(cableLen-locObs)))./(1-r1.*r2.*exp(-2*gamma.*cableLen));
iPropModelF = 1/2.*exp(-gamma.*cableLen).*(exp(gamma.*(cableLen-locObs))-r2.*exp(-gamma.*(cableLen-locObs)))./(Zcable.*(1-r1.*r2.*exp(-2*gamma.*cableLen)));
% use the voltage pulse as input source of the transmission model
uPropModelF = uPropModelF.*(exp(gamma.*locPD)-r1.*exp(-gamma.*locPD)).*uGaussF;
iPropModelF = iPropModelF.*(exp(gamma.*locPD)-r1.*exp(-gamma.*locPD)).*uGaussF;
% alternatively use the current pulse as input source
% uPropModelF = uPropModelF.*(exp(gamma.*locPD)+r1.*exp(-gamma.*locPD)).*iGaussF.*Zcable;
% iPropModelF = iPropModelF.*(exp(gamma.*locPD)+r1.*exp(-gamma.*locPD)).*iGaussF.*Zcable;
else % left hand side solution
uPropModelF = 1/2.*exp(-gamma.*cableLen).*(exp(gamma.*locObs)+r1.*exp(-gamma.*locObs))./(1-r1.*r2.*exp(-2*gamma.*cableLen));
iPropModelF = 1/2.*exp(-gamma.*cableLen).*(-exp(gamma.*locObs)+r1.*exp(-gamma.*locObs))./(Zcable.*(1-r1.*r2.*exp(-2*gamma.*cableLen)));
% use the voltage pulse as input source of the transmission model
uPropModelF = uPropModelF.*(r2.*exp(-gamma.*(cableLen-locPD))-exp(gamma.*(cableLen-locPD))).*uGaussF;
iPropModelF = iPropModelF.*(r2.*exp(-gamma.*(cableLen-locPD))-exp(gamma.*(cableLen-locPD))).*uGaussF;
% alternatively use of the current pulse as input source
% uPropModelF = uPropModelF.*(r2.*exp(-gamma.*(cableLen-locPD))+exp(gamma.*(cableLen-locPD))).*iGaussF.*Zcable;
% iPropModelF = iPropModelF.*(r2.*exp(-gamma.*(cableLen-locPD))+exp(gamma.*(cableLen-locPD))).*iGaussF.*Zcable;
end
%% inverse fourier transform of the resulting voltage signal - alternatively use the resulting current signal
[tPropModel,uPropModelT] = invfourier(f,uPropModelF);
% [~,iPropModelT] = invfourier(f,iPropModelF);
%% example plots
% shifting parameter
width = T*1e09*200;
offset = T*1e09*500; % offset for time domain - pulses should be at zero time
varOffset = T*1e09*max(find(uPropModelT == max(uPropModelT)) - find(uGaussT == max(uGaussT)));
% variable offset between model und measured initial pulse
% labels
labelCharge = ['$~' char(string(charge)) '\,\mathrm{pC}~$'];
labelCableLen = ['$~' char(string(cableLen)) '\,\mathrm{m}~$'];
%% plots for comparing measured calibrator pulse and the fitted gaussian model
figure('Color','white','rend','painters','pos',[400 250 900 400])
% time domain comparison
subplot(1,2,1)
plot(t*1e09-offset,uGaussT,t*1e09-offset,uCalMeasT,'LineWidth',1.5)
ylabel('Voltage $u_{\mathrm{cal}}$ in V')
xlim([t(end)*1e09*0.5-width-offset t(end)*1e09*0.5+width-offset])
xlabel('Time $t$ in ns')
set(gca,'FontSize',15)
grid on
% frequency domain comparison - amplitude spectrum
subplot(1,2,2)
semilogx(f,20*log10(abs(uGaussF)/max(abs(uGaussF))),f,20*log10(abs(uCalMeasF)/max(abs(uGaussF))),'LineWidth',1.5)
%yline(20*log10(mean(abs(uGaussF(1:5)))/max(abs(uGaussF)))-6,'-',sprintf('$f_{-6dB} =$ %.2f MHz',interp1(20*log10(abs(uGaussF)/max(abs(uGaussF))),f,20*log10(mean(abs(uGaussF(1:5)))/max(abs(uGaussF)))-6)/1e06),'LabelHorizontalAlignment','center','Interpreter','latex','FontSize',14);
ylabel('VSD $U_{\mathrm{cal,dB}}$ in $\mathrm{dB}$')
xlim([0 10e07])
xlabel('Frequency $f$ in Hz')
legend('Model','Measurement','Location','SouthWest')
set(gca,'FontSize',15)
grid on
%sgtitle(['PD calibrator' labelCharge 'input pulse in the time and frequency domain'],'FontSize',15)
%% comparison of input pulse with the same pulse after one propagation through the cable length
figure('Color','white','rend','painters','pos',[400 250 900 400])
% time domain comparison
subplot(1,2,1)
plot(t*1e09-offset-(t(uGaussT==max(uGaussT))*1e09-offset),uGaussT,'-.')
hold on
plot(tPropModel*1e09-varOffset-offset,uPropModelT,'LineWidth',1.5)
ylabel('Voltage $u_{2}$ in V')
xlim([t(end)*1e09*0.5-width-offset t(end)*1e09*0.5+width-offset])
xlabel('Time $t$ in ns')
set(gca,'FontSize',15)
grid on
% frequency domain comparison - amplitude spectrum
subplot(1,2,2)
semilogx(f(1),20*log10(abs(uGaussF(1))/max(abs(uGaussF)))-6,'-.') % Fake line for correct legend
hold on
semilogx(f,20*log10(abs(uPropModelF)/max(abs(uPropModelF))),'LineWidth',1.5)
%yline(20*log10(mean(abs(uPropModelF(1:5)))/max(abs(uPropModelF)))-6,'-',sprintf('$f_{-6dB} =$ %.2f MHz',interp1(20*log10(abs(uPropModelF)/max(abs(uPropModelF))),f,20*log10(mean(abs(uPropModelF(1:5)))/max(abs(uPropModelF)))-6)/1e06),'LabelHorizontalAlignment','center','Interpreter','latex','FontSize',14);
ylabel('VSD $U_{2,\mathrm{dB}}$ in $\mathrm{dB}$')
xlim([0 10e07])
xlabel('Frequency $f$ in Hz')
legend('Input pulse','Pulse after transmission','Location','SouthWest')
set(gca,'FontSize',15)
grid on
%sgtitle([labelCharge 'pulse after transmission on' labelCableLen 'of cable in the time and frequency domain'],'FontSize',15)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Martin Fritsch (2021) Transmission Model for MV power cables - Mar 3, 2021 10:35























 834
834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








