基于径向基函数 （RBF） 神经网络的麦基格拉斯时间序列预测（Matlab代码实现）

 💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

基于径向基函数（RBF）神经网络的麦基格拉斯时间序列预测研究

一、麦基格拉斯时间序列的定义与特性

二、径向基函数（RBF）神经网络的基本原理

三、RBF神经网络在MG时间序列预测中的应用

1. 传统RBF方法

2. 改进型RBF方法

四、实验性能与对比分析

1. 评估指标

2. 参数敏感性

3. 与其他模型的对比

五、研究趋势与挑战

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

基于径向基函数（RBF）神经网络的麦基格拉斯时间序列预测研究

在本文中，实现了一个径向基函数（RBF）神经网络，用于预测混沌时间序列预测。特别是设计了一种麦基格拉斯时间序列预测模型，该模型可以使用过去的时间样本预测前进几步的值。RBF 使用传统的梯度下降学习算法进行训练，核函数是从 K 均值聚类算法获得的中心和扩散的高斯核。

一、麦基格拉斯时间序列的定义与特性

麦基格拉斯（Mackey-Glass, MG）时间序列是一种经典的混沌动力学模型，由Michael Mackey和Leon Glass于1977年提出，最初用于模拟血液中白细胞数量的动态调节过程。其数学模型为一阶非线性时滞微分方程：

其中，参数通常取值为 c1=0.1, c2=0.2， p=10，而时延参数 ττ 决定系统的动力学行为：当 τ>16.8 时，系统进入混沌状态，表现出对初始条件的高度敏感性和长期不可预测性。MG时间序列因其复杂的非线性特性，被广泛用于评估时间序列预测模型的性能，尤其在神经形态计算、深度学习等领域作为标准基准。

二、径向基函数（RBF）神经网络的基本原理

RBF神经网络是一种三层前馈网络，由输入层、隐含层和输出层构成：

1. 输入层：接收低维时间序列数据（如历史时间步的MG序列值）。
2. 隐含层：通过径向基函数（如高斯函数将输入映射到高维空间，解决低维空间中的线性不可分问题。
3. 输出层：对隐含层输出进行线性加权组合，生成预测值。

训练过程包括两个阶段：

• 无监督学习：通过K均值聚类确定隐含层中心 cici​ 和宽度 σiσi​；
• 监督学习：使用最小二乘法或梯度下降法优化输出层权重。

优势：

• 全局逼近能力，无局部极小问题；
• 训练速度快，适用于实时预测；
• 对噪声数据具有鲁棒性。

三、RBF神经网络在MG时间序列预测中的应用

1. 传统RBF方法

• 模型构建：以历史时间序列片段（如 x(t),x(t−Δt),…x(t),x(t−Δt),…）作为输入，预测未来单步或多步值。例如，文献[34]采用嵌入维数 m=4m=4、延迟时间 τ=6τ=6 重构相空间，输入向量为 Xi=(xi,xi−6,xi−12,xi−18)Xi​=(xi​,xi−6​,xi−12​,xi−18​)，输出为 xi+kxi+k​（kk 为预测步长）。
• 训练优化：利用梯度下降算法调整权重，结合K均值聚类初始化隐含层参数。

2. 改进型RBF方法

为提升预测精度，研究者提出了多种优化策略：

• 参数优化算法：
  • 粒子群优化（PSO） ：优化隐含层中心和宽度。例如，文献[46]采用混合PSO算法，相比标准K均值和遗传算法，预测误差降低15%以上。
  • 量子粒子群优化（QPSO） ：在混沌时间序列预测中，QPSO训练的RBF网络收敛速度更快，精度更高。
• 结构改进：
  • 梯度RBF（GRBF） ：通过检测时间序列的梯度变化，增强对非平稳数据的适应性。实验表明，GRBF在MG序列的多步预测中误差显著低于传统RBF。
  • 自适应RBF（ROLS-RRBF） ：结合递推正交最小二乘法（ROLS），动态调整网络结构，测试误差较标准RBF减少30%。

    

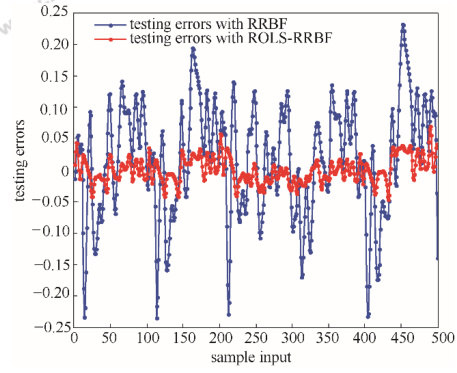
• 混合模型：
  • RBF与模糊逻辑结合：利用模糊规则库优化输入特征，适用于高噪声环境下的MG序列预测。
  • RBF与长短期记忆网络（LSTM）结合：通过LSTM捕捉长期依赖关系，RBF处理局部非线性，提升复杂混沌模式的预测能力。

四、实验性能与对比分析

1. 评估指标

常用指标包括均方根误差（RMSE）、平均绝对百分比误差（MAPE）和相关系数。例如：

• 文献[29]对比了神经网络（NN）、预测增强权重神经网络（PEC-WNN）等模型，在MG序列的 x+84x+84 步预测中，PEC-WNN的MAPE为4.872%，显著优于传统NN的15.263%。

  

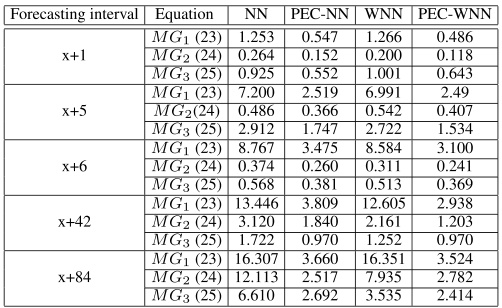
• 文献[46]显示，混合PSO-RBF的RMSE为0.021，而标准RBF为0.035。

2. 参数敏感性

• 时延参数 ττ ：τ=17 时序列呈现典型混沌特性，预测难度显著高于 τ<16.8τ<16.8 的周期状态。
• 隐含层节点数：节点过少导致欠拟合，过多则增加计算复杂度。文献[34]建议节点数大于输入变量数，并通过交叉验证确定最优值。

3. 与其他模型的对比

• 与BP神经网络对比：RBF的训练速度更快，且对初值不敏感。文献[32]在噪声水平为10%时，RBF的RMSE较BP低22%。
• 与LSTM对比：RBF在短期预测（如 k=1k=1）中表现更优，但LSTM在长期预测（k>10k>10）中因记忆门机制更具优势。

五、研究趋势与挑战

1. 趋势：

   • 神经形态硬件加速：利用忆阻器（Memristor）实现RBF网络的硬件化，提升实时预测效率。
   • 多模态数据融合：结合外部环境变量（如温度、压力）扩展MG模型，增强现实适用性。
   • 可解释性增强：通过可视化隐含层激活模式，解析RBF网络的决策逻辑。

2. 挑战：

   • 长期预测精度：混沌系统的内在不稳定性导致多步预测误差累积，需结合混沌控制理论改进模型。
   • 小样本学习：数据不足时，RBF易过拟合，需引入迁移学习或数据增强技术。

六、结论

RBF神经网络凭借其局部逼近特性和快速训练能力，在MG混沌时间序列预测中展现出显著优势。通过优化算法改进网络参数、结合混合模型增强泛化能力，RBF在短期预测任务中表现卓越。未来研究需进一步探索其在复杂动态系统和大规模时序数据中的适用性，并推动硬件实现与理论创新的深度融合。

📚2 运行结果

部分代码：

%%  Results
% Input and output signals (training phase)
figure
plot(indt,f_train,'k','linewidth',lw);
hold on;
plot(indt,y_train,'.:b','linewidth',lw);
xlim([start_of_series_tr+time_steps end_of_series_tr]);
h=legend('Actual Value (Training)','RBF Predicted (Training)','Location','Best');
grid minor
xlabel('Sample #','FontSize',fsize);
ylabel('Magnitude','FontSize',fsize);
set(h,'FontSize',12)
set(gca,'FontSize',13)
saveas(gcf,strcat('Time_SeriesTraining.png'),'png')

% Input and output signals (test phase)
figure
plot(indts,f_test,'k','linewidth',lw);
hold on;
plot(indts,y_test,'.:b','linewidth',lw);
xlim([start_of_series_ts+time_steps end_of_series_ts]);
h=legend('Actual Value (Testing)','RBF Predicted (Testing)','Location','Best');
grid minor
xlabel('Sample #','FontSize',fsize);
ylabel('Magnitude','FontSize',fsize);
set(h,'FontSize',12)
set(gca,'FontSize',13)
saveas(gcf,strcat('Time_SeriesTesting.png'),'png')

% Objective function (MSE) (training phase)
figure
plot(start_of_series_tr:end_of_series_tr-1,10*log10(I(1:end_of_series_tr-start_of_series_tr)),'+-b','linewidth',lw)
h=legend('RBF (Training)','Location','North');
grid minor
xlabel('Sample #','FontSize',fsize);
ylabel('MSE (dB)','FontSize',fsize);
set(h,'FontSize',12)
set(gca,'FontSize',13)
saveas(gcf,strcat('Time_SeriesTrainingMSE.png'),'png')

% Objective function (MSE) (test phase)
figure
plot(start_of_series_ts+time_steps:end_of_series_ts,10*log10(I(end_of_series_tr-start_of_series_tr+1:end)),'.:b','linewidth',lw+1)
h=legend('RBF (Testing)','Location','South');
grid minor
xlabel('Sample #','FontSize',fsize);
ylabel('MSE (dB)','FontSize',fsize);
set(h,'FontSize',12)
set(gca,'FontSize',13)
saveas(gcf,strcat('Time_SeriesTestingMSE.png'),'png')

% Mean square error
10*log10(((f_train'-y_train)*(f_train'-y_train)')/length(y_train))
10*log10(((f_test'-y_test)*(f_test'-y_test)')/length(y_test))

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现