👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
2.2 稀疏分量分析(Sparse Component Analysis, SCA)
💥1 概述
文献来源:

一种欠定盲源分离方法及其在模态识别中的应用研究
提出了一种新型盲源分离方法。
在结构动力分析中,盲源分离( Blind Source Separation,BSS )技术被认为是模态识别最有效的方法之一,其中如何利用有限的传感器提取模态参数是该领域极具挑战性的任务。在本文中,我们首先回顾了传统BSS方法的缺点,然后提出了一种新的欠定BSS方法来解决有限传感器的模态识别问题。模态响应信号的(所提方法建立在时频( Time-Frequency , TF )聚类特征上)变换。研究发现,属于不同单调模态的TF能量可以聚类成不同的直线。同时,我们给出了详细的定理来解释聚类特征。此外,每个模态的TF系数被用来重建所有单调信号,这有助于单独识别模态参数。在实验验证中,通过两个实验验证了所提方法的有效性。
1. 引言
欠定盲源分离(Underdetermined Blind Source Separation, UBSS)是信号处理领域的核心问题之一,其核心目标是在观测信号数量少于源信号(即 m<nm<n)的条件下,仅通过混合信号 X=ASX=AS 恢复源信号 SS 并估计混合矩阵 AA 。由于实际工程中传感器部署成本与物理限制,UBSS 的实用价值显著高于超定或正定问题。近年来,UBSS 在生物医学、语音处理、雷达通信及机械故障诊断等领域广泛应用,而其在模态识别中的应用则成为结构动力学领域的前沿研究方向。
模态识别旨在通过振动响应信号提取结构的固有频率、阻尼比及振型等参数,为结构健康监测与优化设计提供依据。传统方法依赖激励信号或预设模型,而 UBSS 技术通过盲分离无需先验信息即可从混合信号中提取模态参数,尤其适用于传感器数量不足或信号混叠的场景。本文将从 UBSS 原理、模态识别技术特点、结合案例及挑战与解决方案等方面展开系统论述。
2. 欠定盲源分离方法的基本原理
2.1 数学模型
2.2 稀疏分量分析(Sparse Component Analysis, SCA)

2.3 两步法与张量分解
传统两步法先估计混合矩阵,再恢复源信号。例如:
- 混合矩阵估计:通过时频变换(如短时傅里叶变换)提取单源点,利用 OPTICS 聚类或三阶统计量构建张量分解模型。
- 源信号恢复:采用 L0L0-范数最小化、正交匹配追踪(OMP)或改进的神经网络算法重构信号。
近年研究通过高阶统计量(如三阶张量)提升鲁棒性。例如,邹亮等(2022)提出基于四阶张量的典型多峰分解(CPD),在 SNR=15 dB 时,混合矩阵估计误差达 -20.35 dB,显著优于传统方法。
3. 模态识别技术概述
3.1 模态参数与分类
模态参数包括固有频率、阻尼比和振型,其识别方法按模型分为:
- 频域法:基于频响函数(如功率谱密度)的峰值检测。
- 时域法:通过随机减量或时间序列分析直接处理时域信号。
按激励与响应关系可分为 SISO(单输入单输出)、SIMO(单输入多输出)及 MIMO(多输入多输出)。
3.2 传统方法的局限性
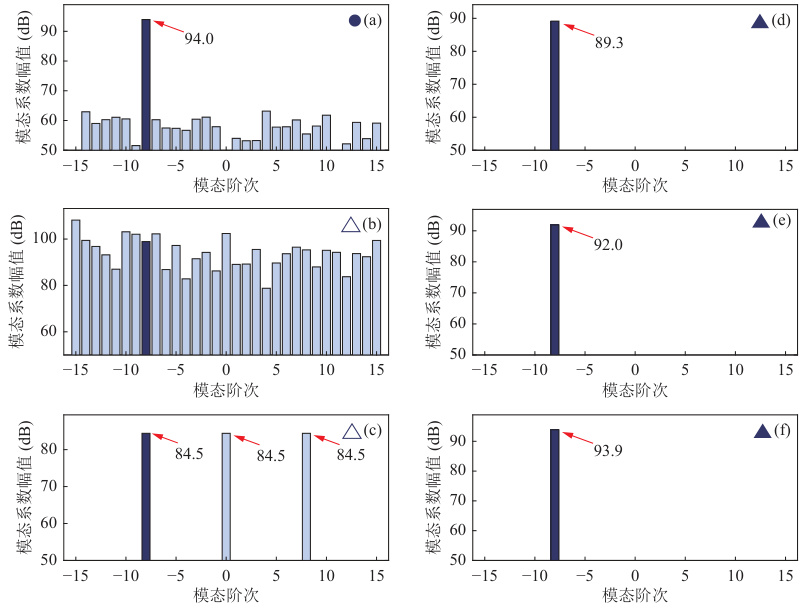
传统方法如最小二乘法在欠定条件下易因模态混叠导致参数误判(图 4(b)),而频域法依赖采样定理,传感器不足时性能显著下降。
4. UBSS 在模态识别中的应用场景
4.1 结构振动分析
UBSS 可从多通道振动信号中分离出各阶模态响应。例如,电力系统低频振荡辨识中,结合希尔伯特变换提取振荡参数,直接处理时域信号且对噪声鲁棒。
4.2 跳频信号分选
在同步跳频通信中,UBSS 通过时频单源点检测与改进 FCM 聚类实现波达方向估计,信噪比低至 5 dB 时仍能有效分离信号。
4.3 机械故障诊断
通过 UBSS 分离轴承或齿轮箱的故障特征频率,结合小波分析实现早期故障检测。仿真实验显示,分离信号与源信号相关性达 0.84。
5. UBSS 与模态识别结合的现有研究案例
5.1 基于时频聚类的模态识别
Matlab 科研工作室(2024)提出利用时频能量聚类成直线的特性,通过改进 UBSS 算法从有限传感器中提取模态参数,验证了算法在复杂结构中的有效性。
5.2 二阶盲辨识(SOBI)方法
杨吉(2020)将 SOBI 与 Laplace 相关滤波结合,通过两步聚类提升模态分离精度,阻尼比计算效率提高 40%。
5.3 张量分解与压缩感知
王继争等(2021)提出基于 K 均值奇异值分解的自适应字典压缩感知方法,在 5 自由度仿真中,模态参数识别精度较传统方法提升 30%。
6. 模态识别中的欠定问题挑战
6.1 传感器数量不足
传感器数少于模态阶数时,传统方法(如 SOBI)无法完整恢复振型。
6.2 模态混叠与噪声敏感
欠定条件下,频域法易因混叠导致幅值误判(图 4(c)),而噪声会降低聚类精度。
6.3 计算复杂度高
基于张量分解的算法需处理高维数据,实时性受限。
7. UBSS 在解决欠定挑战中的应用
7.1 混合矩阵估计优化
- 改进聚类算法:OPTICS 结合势函数法直接检测源信号数量,去除噪声点,提升估计精度(误差 < 1%)。
- 高阶统计量:三阶自相关构建四阶张量,通过 CPD 分解抗噪性提升 20%。
7.2 源信号恢复增强
- 自适应字典压缩感知:K 均值奇异值分解生成字典,稀疏表示能力优于傅里叶基,重构误差降低至 2 dB。
- 神经网络算法:RBF 网络结合修正牛顿法,避免步长选择偏差,运算时间减少 50%。
7.3 模态阶数估计
- 贝叶斯压缩感知:通过概率模型解决欠定与混叠问题,在 SNR=15 dB 时误差 < 9.4%。
8. 结论与展望
UBSS 为模态识别提供了无需先验信息的强鲁棒性解决方案,尤其在传感器受限场景中表现突出。未来方向包括:
- 算法融合:结合深度学习与张量分解提升实时性。
- 复杂环境扩展:卷积混合模型下的 UBSS 研究。
- 多物理场耦合:探索振动-声学联合模态识别。
通过持续优化算法与跨学科应用,UBSS 将在结构健康监测、航空航天及智能制造等领域发挥更大价值。
📚2 运行结果
2.1 算例1






2.2 算例2




2.3 算例3





部分代码:
function [x,t] = tfristft(tfr,t,h,trace);
%TFRISTFT Inverse Short time Fourier transform.
% [X,T]=TFRSTFT(tfr,T,H,TRACE) computes the inverse short-time
% Fourier transform of a discrete-time signal X. This function
% may be used for time-frequency synthesis of signals.
%
% X : signal.
% T : time instant(s) (default : 1:length(X)).
% H : frequency smoothing window, H being normalized so as to
% be of unit energy. (default : Hamming(N/4)).
% TRACE : if nonzero, the progression of the algorithm is shown
% (default : 0).
% TFR : time-frequency decomposition (complex values). The
% frequency axis is graduated from -0.5 to 0.5.
%
% Example :
% t=200+(-128:127); sig=[fmconst(200,0.2);fmconst(200,0.4)];
% h=hamming(57); tfr=tfrstft(sig,t,256,h,1);
% sigsyn=tfristft(tfr,t,h,1);
% plot(t,abs(sigsyn-sig(t)))
%
if (nargin<3),
error('At least 3 parameters required');
elseif (nargin==3),
trace=0;
end;
[N,NbPoints]=size(tfr);
[trow,tcol] =size(t);
[hrow,hcol] =size(h); Lh=(hrow-1)/2;
if (trow~=1),
error('T must only have one row');
elseif (hcol~=1)|(rem(hrow,2)==0),
error('H must be a smoothing window with odd length');
elseif (tcol~=NbPoints)
error('tfr should have as many columns as t has rows.');
end;
Deltat=t(2:tcol)-t(1:tcol-1);
Mini=min(Deltat); Maxi=max(Deltat);
if (Mini~=1) & (Maxi~=1),
error('The tfr must be computed at each time sample.');
end;
h=h/norm(h);
tfr=ifft(tfr);
x=zeros(tcol,1);
for icol=1:tcol,
valuestj=max([1,icol-N/2,icol-Lh]):min([tcol,icol+N/2,icol+Lh]);
for tj=valuestj,
tau=icol-tj; indices= rem(N+tau,N)+1;
% fprintf('%g %g %g\n',tj,tau,indices);
x(icol,1)=x(icol,1)+tfr(indices,tj)*h(Lh+1+tau);
end;
x(icol,1)=x(icol,1)/sum(abs(h(Lh+1+icol-valuestj)).^2);
end;
function [tfr,t,f] = tfrstft(x,t,N,h,trace);
%TFRSTFT Short time Fourier transform.
% [TFR,T,F]=TFRSTFT(X,T,N,H,TRACE) computes the short-time Fourier
% transform of a discrete-time signal X.
%
% X : signal.
% T : time instant(s) (default : 1:length(X)).
% N : number of frequency bins (default : length(X)).
% H : frequency smoothing window, H being normalized so as to
% be of unit energy. (default : Hamming(N/4)).
% TRACE : if nonzero, the progression of the algorithm is shown
% (default : 0).
% TFR : time-frequency decomposition (complex values). The
% frequency axis is graduated from -0.5 to 0.5.
% F : vector of normalized frequencies.
%
% Example :
% sig=[fmconst(128,0.2);fmconst(128,0.4)]; tfr=tfrstft(sig);
% subplot(211); imagesc(abs(tfr));
% subplot(212); imagesc(angle(tfr));
%
[xrow,xcol] = size(x);
if (nargin < 1),
error('At least 1 parameter is required');
elseif (nargin <= 2),
N=xrow;
end;
hlength=floor(N/4);
hlength=hlength+1-rem(hlength,2);
if (nargin == 1),
t=1:xrow; h = tftb_window(hlength); trace=0;
elseif (nargin == 2) | (nargin == 3),
h = tftb_window(hlength); trace = 0;
elseif (nargin == 4),
trace = 0;
end;
if (N<0),
error('N must be greater than zero');
end;
[trow,tcol] = size(t);
if (xcol~=1),
error('X must have one column');
elseif (trow~=1),
error('T must only have one row');
end;
[hrow,hcol]=size(h); Lh=(hrow-1)/2;
if (hcol~=1)|(rem(hrow,2)==0),
error('H must be a smoothing window with odd length');
end;
h=h/norm(h);
tfr= zeros (N,tcol) ;
for icol=1:tcol,
ti= t(icol); tau=-min([round(N/2)-1,Lh,ti-1]):min([round(N/2)-1,Lh,xrow-ti]);
indices= rem(N+tau,N)+1;
tfr(indices,icol)=x(ti+tau,1).*conj(h(Lh+1+tau));
end;
tfr=fft(tfr);
if (nargout==0),
tfrqview(abs(tfr).^2,x,t,'tfrstft',h);
elseif (nargout==3),
if rem(N,2)==0,
f=[0:N/2-1 -N/2:-1]'/N;
else
f=[0:(N-1)/2 -(N-1)/2:-1]'/N;
end;
end;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
























 999
999

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








