数量关系：高频考点常用解题方法（一）

请点击↑关注、收藏，本博客免费为你获取精彩知识分享！有惊喜哟！！

数量关系 1.高频考点常用解题方法-代入法

测查报考者理解、把握事物间量化关系和解决数量关系问题的能力，主要涉及数据关系的分析、推理、判断、运算等。

其中：

理解把握量化关系：即从题干中找是否有等量关系或者其他可以量化的关系，将文字语言尽量转化为数字语言；

解决数量关系问题：即在把握了题干中数量之间的关系的基础上，解决设问中所提出的问题；

那怎么解决呢？

对给定的数据关系进行分析、推理、判断、运算等。

总结一下：

所谓数量关系：

就是给定一些量，比如涉及年龄、数字、行程、工程、溶液等；

给定这些量之间存在的关联关系，这些关系表现为数据之间关联，找到数据之间的关联之后，用对方法将其解出来。

所以我们将数量关系的学习，拆解为两大块：

一块是解什么，一块是怎么解；

鉴于数量关系中出现的题型非常之多，当然有高频考点，也有非高频考点；但是无论什么考点，涉及的解题方法却存在共性；

所以我们先来介绍数量关系涉及的解题方法。

常用解题方法：

一般而言，常用到的方法有如下几种：

代入法、数字特性法、方程法。

代入法说来我们并不陌生，在资料分析中我们也介绍过，也用过，还挺好用～

那在数量关系中，它就更好用啦～

代入法，顾名思义，就是将选项中的数据代入题干，验证是否符合题干给定的“关联”，不符合即验证失败，转换目标验证下一个。

那什么时候用代入法？

记住以下情形：

第一类：固定题型

涉及年龄、多位数、余数、不定方程等；

第二类：不知所措型

(1)看完题干不知道从哪里入手，观察选项，选项如果有两个以上的数，那抓紧从题干找两组数之间的关系，验证该关系；

(2)如果通过其他方法剩下了2个选项，那也赶紧代入验证，可能就出答案了；

(3)那如果什么都没有呢？

代入试试，不行拉倒，换个题目还是条好汉。

第一个代入谁验证？

观察是否有这些特殊字眼：最大、最小、至多、至少；

如果问最大或至多，那咱从选项中的大数字开始验证，为啥？

那你要是验证小的验证通过了，能保证更大的数据就不会验证通过么？

难不成从小到大验证出4个、3个、2个了，再选个大的么？

所以问最大，从最大开始验证；

问最小，从最小开始验证。

例1：某食品厂速冻饺子的包装有大盒和小盒两种规格，现生产了11000 只饺子，恰好装满 100 个大盒和 200 个小盒。若 3 个大盒与 5 个小盒装的饺子数量相等，则每个小盒与每个大盒装入的饺子数量分别是：

A.24 只、40 只 B. 30 只、50 只 C. 36 只、60 只 D. 27 只、45 只

解析：

选项均为2个数字，考虑代入法；

回题干找数据和关系：

根据圈画可推知大盒、小盒可装入饺子的数量比例关系为5:3，验证发现都符合；

那就一一代入试算，A选项24*200+40*100=8800，排除；

B选项，30*200+50*100=11000，正确，当选。

答案选B。

例2：一个五位数，左边三个数是右边两位数的5倍，如果把右边的两个数移到前面，则所得新的五位数要比原来的五位数的2倍还多 75，则原来的五位数是（）

A.13527 B.18036 C.12525 D.27545

解析：

题干给定多位数之间的关系，考虑代入法；

根据圈画，验证后两位的5倍是否与前三位相同，据此排除D选项；

继续看题干，找数据之间的关系：

根据条件：

新的五位数比原来的五位数的2倍还多75，那我们来验证原来的数的2倍加上75的末位，是否与第三位相同，验证可知A、B均不同，故答案选C。

例3：某汽车厂商生产甲、乙、丙三种车型，其中乙型产量的3 倍与丙型产量的 6 倍之和等于甲型产量的 4 倍，甲型产量与乙型产量的 2 倍之和等于丙型产量 7 倍。则甲、乙、丙三型产量之比为（ ）

A．5∶4∶3 B．4∶3∶2 C．4∶2∶1 D．3∶2∶1

解析：

选项均为3个数字，考虑代入法；

回题干找数据和对应关系：

根据题干中的条件对选项进行对应验证，可知A、B、C都错，答案选D。

例4：在一堆桃子旁边住着5 只猴子。深夜，第一只猴子起来偷吃了一个，剩下的正好平均分成 5 份，它藏起自己的一份，然后去睡觉。过了一会儿，第二只猴子起来也偷吃了一个，剩下的也正好平均分成 5 份，它也藏起自己的一份，然后去睡觉，第三、第四、第五只猴子也都依次这样做。

问那堆桃子最少有多少个？（ ）

A．4520 B．3842 C．3121 D．2101

解析：

设问问“最少”，尝试代入法；

先看题干中的数据和关系：

首先判定总数尾数为1，排除A和B；

代入验证，因问“最小”，则从小的开始验证，即根据剩下的条件先验证D选项：

条件为：被藏起1份后，还余4份，故4份总和尾数为1或6；

(2101-1)/5=2100/5=420,其中一份为420，4份总和为420*4=8400，不满足条件，排除，答案为C。

以上就是代入法的应用；

记住适用情形，找准数量关系，看清设问对象，代入速速排除。

数量关系 2.高频考点常用解题方法-数字特性法

常用解题方法-数字特性法：

什么是数字特性？

所谓数字特性，实际上就是数字本身的性质和数字之间的运算关系；

那有哪些常见的数字特性？

奇偶、质数合数、整除、余数、倍数及数列等；

数字特性如何应用？

数字特性，归根到底是一种特殊的代入法，即通过为选项数字找特征，将其与题干给定的条件进行匹配，匹配失败即验证失败，转换目标验证下一个。

接下来我们就对几种常见的数字特性展开介绍，本篇先看奇偶、质数合数和整除；

1.奇偶性：

奇数和偶数相信小伙伴们一定不陌生，无非就是这个自然数2不2的问题；

奇数不2，偶数2；（奇数不能被2整除、偶数能被2整除）。

那奇数和偶数有什么特性？

什么时候考虑奇偶性呢？

2.质数和合数

首先明确自然数存在这样一种分类：质数、合数和1；

其中：

质数定义：在大于1的自然数中，除了1和它本身以外不再有其他因数的数，又称为素数。

如：2、3、5、7、11、13、17、19、23.....

合数定义：自然数中除了能被1和本身整除外，还能被其他数（0除外）整除的数；

如：4、6、8、9、12、14、15....

而1：既不是质数和不是合数。

质数和合数的考查并不多，但要明确概念，以免看到质数、素数、合数的时候慌慌张张。

3.整除

注意上式中，只有B不能为0，A和C均可以为0；

也就是说，0能被任何非0的整数整除。

在整除特性中，我们需要掌握常见的整除判定法则：

能被2整除的数：末位可以被2整除；

能被3整除的数：各位数字之和能被3整除；

能被4（或25）整除的数：末二位可以被4（或25）整除；

能被5整除的数：末位可以被5整除（即末位为0或5）；

能被8（或125）整除的数：末三位可以被8（或125）整除；

能被9整除的数：各位数字和能被9整除；

且有：

所以当题干中出现各个位数之和、

出现2、3、4、5、8、9等的倍数、平均分配等，

记得使用判定法则哟。

了解了以上特性，我们一起来看例题，把特性们拉出来遛遛。

例1：一个人到书店购买了一本书和一本杂志，在付钱时，他把书的定价中的个位上的数字和十位上的看反了，准备付21 元取货。售货员说:“您应该付39 元才对。”

请问书比杂志贵多少钱？（ ）

A. 20 B. 21 C. 23 D. 24

解析：

题干出现两本书的价格之和，考虑奇偶性；

两数和为奇数，则差亦为奇数；

看选项，排除A和D；

剩下2个选项咋办？别忘了代入呐；

代入B选项试算，书+杂志=39，书-杂志=21，

则书=（39+21）／2=30；

书的个位和十位被看反，则被看成了03元？

...先不嘲笑他，继续验证：

杂志没看错，价格为21-03=18元，杂志+书=48元，与题干条件不符，排除。

答案选C。

例2：四年级有4 个班，不算甲班其余三个班的总人数是 131 人；不算丁班其余三个班的总人数是 134 人；乙、丙两班的总人数比甲、丁两班的总人数少1 人。

问这四个班共有多少人？（ ）

A. 177 B. 178 C. 264 D. 265

解析：

题干中出现三个班级的和，人数之差，考虑奇偶性；

（乙+丙）-（甲+丁）=1；

则（乙+丙）+（甲+丁）亦应为奇数；

看选项，排除B、C；

剩下两个选项怎么办？代入验证呐：

一看题中：

乙+丙=丁=131，甲+乙+丙=134，131+134=265....，

感谢出题人给了这么好的一个选项，排除D，答案选A。

例3：为响应国家“做好重点群体就业工作”的号召，某企业扩大招聘规模，计划在年内招聘高校毕业生 240 名，但实际招聘的高校毕业生数量多于计划招聘的数量。已知企业将招聘到的高校毕业生平均分配到 7 个部门培训，并在培训结束后将他们平均分配到 9 个分公司工作。

问该企业实际招聘的高校毕业生至少比计划招聘数多多少人（ ）：

A.6 B.12 C.14 D.28

解析：

题干出现平均分配，考虑整除；

看题干的条件，实际招聘人数为240+某个自然数，且实际招聘人数应为7和9的倍数；

我们对于9的倍数很熟，可以被9整除的数，其各位数之和相加可以被9整除；

将选项代入验证：

A选项：240+6=246，位数之和为14，排除；

B选项：240+12=252，位数之和为9，保留；

并验证252/7=36，验证通过，答案选B。

例4：小李某月请了连续5天的年假，这5天的日期数字相乘为7893600，问他最后一天年假的日期是：

A.25日 B.26日 C.27日 D.28日

解析：

题干出现数字相乘，考虑整除；

看数字7893600，试算位数和为：7+8+9+3+6=33，可知该乘积可以被3整除，不能被9整除。

将选项代入验证：

通过以上例题和解析，希望大家能建立起来对数量关系的信心，给自己一个信念：

一定能找到内在逻辑和解决办法，助我们快速找出那几道容易的题，并且快速选出答案！

数字特性法-倍数：

提到倍数，我们一定能匹配到这样的描述：

A是B的m倍、A是C的n倍还余z等；

用列式描述即为：

A=Bm，A=Cn+z;

可推知：A同是B和m的倍数；A-z为C和n的倍数。

以上是普通的倍数表达，从文字出发很容易找到答案或者转换为列式后找到答案；

除此之外，还有一些倍数的关系是不那么明显被识别的，比如以下描述，你是否能找到其中的倍数关系呢？

我们一起来分析：

先看1，我们将其写作分数的形式，即有：

其中，m和n互质；

也就是需要对A和B进行约分，约分至m和n后，即不能再继续约分了；

假设被约掉的数为k；

则有：A=mk，B=nk；

可知A为m的倍数、B为n的倍数；

此为倍数关系①。

我们继续看：

根据倍数关系①可知，A+B应为m+n的倍数。

同理可推知，A-B应为m-n的倍数。

再看2:

根据倍数关系①可知，B为m的倍数。

继续看3:

球的总数为A，分为若干组，每组有m个黑n个白；

假设将球分为了k组：

则有黑球总数为mk，白球总数为nk；

则有球的总数A=mk+nk=（m+n）k，推知A为（m+n）的倍数。

最后来看4:

A比B多m%，则有：A=B(1+m%),

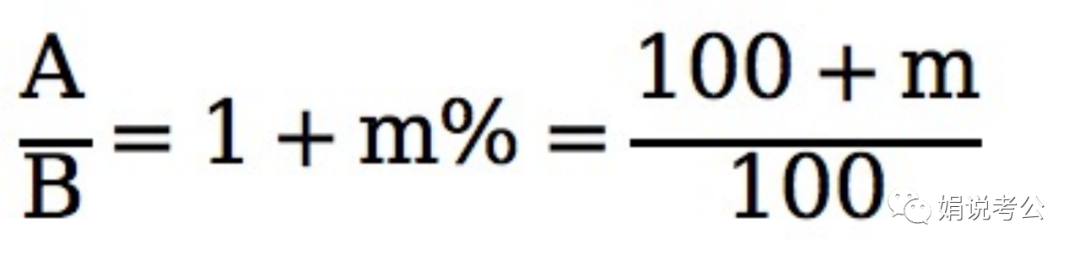
这里要注意了，根据上式我们可以得到的结论是否为：

A为（100+m）的倍数，B为100的倍数？

错错错，非也非也！

还记得分析推导结论①的过程中，对A和B进行过约分么？要约到不能再约的时候，才可以得出倍数关系！

所以涉及到百分数的结论是：

有倍数关系存在，但务必记得要约分到底之后，才能得到倍数关系！！

举个例子：

同理若表达为A比B少m%，则有：A=B(1-m%)；

依然存在倍数关系，但同样要约分到底之后才能得出倍数关系结论。

理清楚上述过程之后，我们一起来看例题。

例1：举办排球比赛，选男员工的1/11 和 12 名女员工，剩余男员工是剩余女员工的2 倍，总员工人数 156 人；

问：男员工有多少人？（ ）

A．100 B．99 C．111 D．121

解析：

题干中出现分数，考虑是否存在倍数关系：

从“选男员工的1/11”，可知男员工的人数应为11的倍数，看选项，排除A、C；

继续看题干剩余条件：

考虑代入法，代入B选项：

男员工为99人，其1/11为9人，即剩余男员工数为90人，则剩余女员工数为45人，女员工总人数为45+12=57人；

总人数为99+57=156人，验证无误，当选；

答案为B。

例2：两个派出所某月内共受理案件160 起，其中甲派出所受理的案件中17%是刑事案件，乙派出所受理的案件中有 20%是刑事案件，问乙派出所在这个月中共受理多少起非刑事案件？

A．48 B．60 C．72 D．96

解析：看题干，出现百分数，考虑是否存在倍数关系：

翻译百分数，即有：

则有甲刑事为17的倍数，甲总数为100的倍数；

由于甲乙案件总量为160，推知甲为100，乙为60；

而乙的案件中并非全部为刑事案件；

看选项，非刑事案件数量只能选A。

例3：甲、乙两个班各有40 多名学生，男女生比例甲班为 5：6，乙班为5：4。则这两个班的男生人数之和比女生人数之和（ ）。

A．多 1 人 B．多 2 人 C．少 1 人 D．少 2 人

解析：

例4：某市服务行业举行业务技能大赛，其中东区参赛人数占总人数的1／5，西区参赛人数占总人数的2／5，南区参赛人数占总人数的 1/4，其余的是北区的参赛人员。结果东区参赛人数的 1/3获奖，西区参赛人数的 1／12获奖，南区参赛人数的1/ 9获奖。

已知参赛总人数超过100 人，不到 200 人，则参赛总人数为（ ）。

A．120 B．140 C．160 D．180

解析：

题干出现分数，考虑利用倍数关系：

整理条件：

参赛总人数应为5的倍数、4的倍数、3的倍数、9的倍数；

看选项：

B和C为5和4的倍数，但并非3的倍数，排除；

A为5、4、3的倍数，但并非9的倍数，排除；

答案选D。

以上就是倍数的相关内容；

在理解了基本逻辑的基础上，通过例题的练习，快速的锁定题干关键信息，利用倍数关系直达正确答案；

在此基础上，大家一定要多多练习，熟悉数量的特性，练就火眼金睛！

数字特性法-余数、数列：

4.余数

在上一篇的倍数中，我们提到过有这种描述：

A是C的n倍还余z，即A=Cn+z；

如果又已知：A是B的m倍还余k，即有A=Bm+k；

在这两个条件基础上，需要选出正确答案；

我们通过倍数的学习知道了可以这样来判断：

判断选项是否满足：

A-z为C、n的倍数，A-k是否为B、m的倍数；

那还有没有别的方法呢？

答案是有！

看下表：

有同学会疑惑这是为什么，娟姐一一举个例子：

(1)余数相同型

例：一个正数A除5余1，除4余1，除9余1；

则该数A满足：

A=5a+1，A=4b+1，A=9c+1，其中（a,b,c均为正整数）；

即有：A-1为5、4、9的倍数；

而5、4、9的最小公倍数为5x4x9=180，

则有：A-1=180n，

则A=180n+1，即A为除数的最小公倍数的n倍+余。

(2)除数与余数之和相同型

例：一个正数A除6余1，除5余2，除4余3；

则该数A满足：

A=6a+1，A=5b+2，A=4c+3，其中（a,b,c均为正整数）；

A=6(a-1)+7，A=5(b-1)+7，A=4(c-1)+7,

即：A-7为6、5、4的倍数；

而6、5、4的最小公倍数为60，则有：A-7=60n，

则A=60n+7，即A为除数的最小公倍数的n倍+和。

(3)除数与余数之差相同型

例：一个正数A除6余5，除5余4，除4余3；

则该数A满足：

A=6a+5，A=5b+4，A=4c+3，其中（a,b,c均为正整数）；

A=6(a+1)-1，A=5(b+1)-1，A=4(c+1)-1,

即：A+1为6、5、4的倍数；

而6、5、4的最小公倍数为60，则有：A+1=60n，

则A=60n-1，即A为除数的最小公倍数的n倍-差。

理解了吧，所以请小伙伴记住表格中的结论，遇到此类题型时即可快速找到答案；

有同学可能会有疑问，那难道余数类的问题就一定是余数相同、和相同和差相同么？万一都不相同呢？咋办？

还能咋办？倍数能用吧？代入能用吧？

不能学僵了哈，一个方法并非只适用一个题目，一个题目并非只能用到一种方法，结合起来，融合起来，去做题练题，让你的思维跑起来！

例1：三位运动员跨台阶，台阶总数在100-150 级之间，第一位运动员每次跨 3 级台 阶，最后一步还剩 2 级台阶。第二位运动员每次跨 4 级台阶，最后一步还剩 3 级台阶。第三 位运动员每次跨 5 级台阶，最后一步还剩 4 级台阶。

则这些台阶总共有多少级（ ）：

A.119 B.121 C．129 D．131

解析：

翻译题干给定条件，即有：

总台阶数满足，除3余2，除4余3，除5余4；

除数与余数之差相同，即：差同减差；

则有：

总台阶数为：60n-1，即总台阶数+1为60的倍数；

看选项：秒A。

例2：某市场调查公司3 个调查组共 40 余人，每组都有 10 余人且人数各不相同。 2017 年重新调整分组时发现，若想分为 4 个人数相同的小组，至少需要新招 1 人；若想分为 5 个人数相同 的小组，至少还需要新招 2 人。

问原来3 个组中人数最多的组比人数最少的组至少多几人？

A. 2 B. 3 C. 4 D. 5

解析：

翻译题干给定条件即有：

总人数满足：除4余3，除5余3；

没问题吧？

除4还缺1，就说明除4的最后一组，是3个呐，不就是除4余1么？

或者除4余（-1），除5余（-2），也是一样可以得到结果的哈；

不信的话我们分别来看：

除4余3，除5余3，则除数和余数满足余数相同，余同加余，总人数为20n+3；

除4余（-1），除5余（-2），则除数和余数满足和相同，和同加和，总人数为20n+3。

题干说明总数为40余人，可知n只能取2，即总数为43人；

最初分组满足“每组都有10 余人且人数各不相同”，问最多比最少至少多几人？

那我们让最少的组尽量人多，如何分配呢？

有：43/3=14...2，若最少为14，则其余两组为15、15，不满足条件；

最少为13，其余两组为14、16，那么最多比最少至少多16-13=3人，答案选B。

例3：某次比赛报名参赛者有213 人，但实际参赛人数不足 200。主办方安排车 辆时，每 5 人坐一辆车，最后多 2 人；安排就餐时，每 8 人坐一桌，最后多 7 人；分组比赛时，每 7 人一 组，最后多 6 人。

问未参赛人数占报名人数的比重在以下哪个范围内？

A.低于 20% B.20%-25%之间

C.25%-30%之间 D.高于 30%

解析：

翻译题干所给条件：

实际参赛人数满足：除5余2，除8余7，除7余6；

由“除8余7、除7余6”可知，差同减差，则，实际参赛人数为：56n-1,且除5余2；

即56n-1-2为5的倍数，即56n-3的末位为0或5，则56n的末位为3或8；

又实际参赛人数不足200人，则n只能取3；

即实际参赛人数为：56x3-1=167人；

则未参赛人数占比为：

（213-167）／213=46/213，截位为46／21=2.1，答案选B。

发现了么？

本题用到了余数、倍数、整除判定和截位直除；

所以学好基础方法，打遍天下都不怕！铁子，加油哦！

到这里，数字特性就还有最后一个内容了，那就是数列；

数列我们都不陌生，最重要的是记住数列的公式和性质，列表如下：

我们一起来看个例题；

例：某成衣厂对9 名缝纫工进行技术评比，9 名工人的得分正好成等差数列，9 人的平均得分是 86 分，前 5 名工人的得分之和是 460 分，那么前 7 名工人的得分之和是多少? （ ）

A．602 B．623 C．627 D．631

解析：

题干出现关键词“等差数列”，考虑可以用等差数列的公式和性质求解：

该数列是奇数数列，平均数即为等差中项，即第5名工人得分为86分；

同理，第3名工人得分为460/5=92分；

可知第4名工人得分为(86+92)／2=89分；

则前7名工人总分应为89x7，末位为3，答案选B。

有同学可能从题干中看出了倍数关系，我们尝试用倍数求解：

前7名工人得分之和一定为7的倍数；

看选项，A选项602/7=86，B选项623/7=89，C和D除不尽，先排除C和D；

而A选项前7名的平均分为86，但题干说9人的平均分为86，所以A选项排除；

答案选B。

以上就是数字特性中的余数和数列，记住结论，尝试推导加深对结论的印象；

在此基础上，做题，总结，尝试用不同的方法去做你所遇到的每一道题，题目是会变的，但是方法是永恒的，熟悉它，用好它，它一定会对你有所回报。

数量关系 3.高频考点常用解题方法-方程法

方程法：

说起来方程法，我们一定都很熟悉很熟悉了，从小学开始就不停的列方程，不停的求解；

一定是什么孽缘，到现在居然又要列方程！

但是在数量关系中，我们列的方程不一定要求解，也不一定能解出来；

一是因为我们所说的方程有一元一次方程及方程组，还有不定方程和方程组；

二是因为方程列好后，我们可以情形利用代入法、倍数关系、奇偶性等快速找到答案。

那什么情形考虑方程法呢？

当题干中具有明显的等量关系时，我们可以用方程法；

当遇到固定题型，如：和差倍比、工程、行程、最值、容斥、比赛、盈亏、年龄等问题时，可以用方程法。

那如何列方程能使我们离答案更近呢？

这就需要我们注意列方程的技巧：

1.优先设所求的量；

2.设未知数可以视给定中间量、分数、百分数、比例等特征倍数放大，避免出现分数、小数点等不甚好算的式子；

3.利用题干给定的关系，尽量减少未知数的个数。

那方程列好了，如何快狠准的利用方程？

1.结合我们的代入法、数字特性、倍数关系等；

2.对于多元方程组，要用好消元法：

当未知数系数倍数关系较明显时，优先考虑加减消元法；

当未知数系数代入关系较明显时，有限考虑代入消元法。

3.也可以采用赋值法，特殊情况如：不定方程组最后问题是求n(x+y+z)时，即可赋值其中任何一个未知数为0进行求解。

理论理顺了，我们一起来看例题，试着列一列方程，找一找答案。

例1：假设空气质量可按良好、轻度污染和重度污染三类划分。一环境监测单位在某段时间对63 个城市的空气质量进行了监测，结果表明：空气质量良好城市数是重度污染城市数的 3 倍还多 3 个，轻度污染城市数是重度污染城市数的 2 倍。

那么，空气质量良好的城市个数是：

A.33 B.31 C.23 D.27

解析： 题干中出现3个未知量之间的等量关系，考虑利用方程法列式；

看设问，求“良好”；

看条件：良好=3被重度+3，轻度=2倍重度；

可知最好假设重度的个数为x，则有：

63=良好+轻度+重度=（3x+3）+2x+x=6x+3，

可求得x=10;

则良好=3x+3=33，答案选A。

例2：甲、乙两个学校的在校生人数之比为5∶3，甲学校如果转入 30 名学生，再将85 名学生转到乙学校，则两个学校在校生人数相同。

则此时乙学校学生人数在以下哪个范围内?

A.不到 200 人 B.在 200—240 人之间 C.在 241—280 人之间 D.超过 280 人

解析：

题干出现未知量之间的比例关系和等量关系，考虑方程法求解；

假设甲校在校生人数为5x，乙校在校人数为3x，

则根据等量关系有列式为：

5x+30-85=3x+85；

移项，合并同类项有：

2x=170-30=140，则x=70；

此时乙校在校生人数为70x3+85=295，答案选D。

例3：某单位组织参加理论学习的党员和入党积极分子进行分组讨论，如果每组分配7 名党员和 3 名入党积极分子，则还剩下 4 名党员未安排；如果每组分配 5 名党员和 2 名入党积极分子，则还剩下 2 名党员未安排。

问参加理论学习的党员比入党积极分子多多少人?

A．16 B．20 C．24 D．28

解析： 题干中出现了2个未知数之间的等量关系，考虑方程法列式；

看设问：问两个未知数之差；

如何假设未知数呢？

从题干中分不同的组，但是总人数相同，我们可以考虑假设两次分组的组数分别为x和y，则有：

可知党员与入党积极分子人数之差为：

7x+4-3x=4x+4=20

答案选B。

有小伙伴可能发现了，题干的表述是一种分组关系，也可以用倍数法来判断，我们一起尝试下：

依然假设两次分组的组数分别为x和y，则有：

则党员与入党积极分子人数之差为：4x+4=3y+2；

可知人数之差满足：是4的倍数，减去2为3的倍数；

看选项，都满足是4的倍数；

但只有B选项满足减2为3的倍数，答案选B。

例4：某部门正在准备会议材料，共有153 份相同的文件，需要装到大小两种文 件袋里送至会场，大的每个能装 24 份文件，小的每个能装 15 份文件。如果要使每个文件袋都正好装满， 则需要大文件袋（ ）个。

A.2 B.3 C.5 D.7

解析： 题干中出现等量关系，考虑方程法列式；

假设需要大文件袋x个，小文件袋y个，则有：

24x+15y=153，

化简得：8x+5y=51，为不定方程，考虑代入法：

代入x的值，得到51-8x的值应为5的倍数，即末位应为0或5；

那么倒推可知：8x的末位应为1或6；排除B、C；

又7代入太大，排除；答案选A。

例5：木匠加工2 张桌子和 4 张凳子共需要 10 个小时，加工 4 张桌子和 8 张椅子需要22 个小时。问如果他加工桌子、凳子和椅子各10 张，共需要多少小时？

A．47.5 B．50 C．52.5 D．55

解析：

题干中出现3个量之间的等量关系，假设加工一张桌子、一张凳子和一张椅子所需时间分别为x、y、z，则有：

求：10（x+y+z）的值，而不定方程组中①+②得：

4x+4y+4z=21,

则有10（x+y+z）=21/4x10=52.5，答案选C。

以上就是我们常用解题方法之方程法；

相信从例题可以看出，方法并非独立的，一定是融合变通的；

所以务必要多刷题，多总结，看到题干中条件的时候可以迅速匹配最佳方法，且在求解的过程中可以快速找到突破。

数量关系 4.高频考点常用解题方法-工程问题

工程问题

1.明确什么样的题是工程问题？

题干中出现“完成一件事／一项工程等...给出了时间或者效率...”

2.核心公式

工程总量=工作时间x工作效率

合作完成时，则有：

工程总量 = 工作效率之和x工作时间

或工程总量 = A工作效率x工作时间 + B工作效率x工作时间

3.解题方法

工程问题类题型中，题干可能出现以下几种条件：

已知工作时间；

已知工作效率之比；

已知不同安排下不同的完成情况；

已知合作完成，但中途出现不同的人不同的参与情况；

......

面对不同的条件，我们都需要从给定的条件出发，寻找最佳的解题途径；

我们为每种条件匹配最佳解题方法如下表：

具体如何求解呢，带着解法，我们一起来看例题；

例1：一项工程，甲、乙合作12 天完成，乙、丙合作 9 天，丙、丁合作 12 天完成。

如果甲、丁合作，则完成这项工程需要的天数是？（ ）

A．16 B．18 C．24 D．26

解析： 题干中只给出了工作时间，考虑赋值工程总量；

工作时间分别为12、9、12，最小公倍数为36；

故赋值工作总量为36，则有：

12（甲+乙）=36，则甲+乙=3①；

9（乙+丙）=36，则乙+丙=4②；

12（丙+丁）=36，则丙+丁=3③。

由此可知，我们得到的是一个不定方程组，4个未知数，但只有3个等式；

再看设问，求甲+丁；

那可以考虑对不定方程进行加减消元，消掉乙、丙，留下甲、丁，即：

①-②+③，则有：

甲+乙-（乙+丙）+丙+丁=甲+乙-乙-丙+丙+丁=甲+丁=3-4+3=2；

则有甲、丁合作时的工作时间为：

工程总量／工作效率之和=36/2=18，答案选B。

例2：有A 和 B 两个公司想承包某项工程，A 公司需要 300 天才能完工，费用为 1.5 万元/天，B 公司需要 200 天就能完工，费用为 3 万元/天，综合考虑时间和费用问题，在 A 公司开工 50 天后，B 公司才加入工程，按以上方案，该项工程的费用为多少？

A.475 万元 B.500 万元 C.525 万元 D.615 万元

解析： 题干为工程问题，在总量、效率和时间中，只出现了工作时间，考虑赋值工作总量；

工作时间分别为：300天和200天，最小公倍数为600天；

则赋值工作总量为600，则有：

A公司的工作效率为600/300=2，B公司的工作效率为600/200=3；

根据题干条件：

A公司开工50天后，完成工程量为50x2=100；

剩余工程量为600-100=500；

A、B两公司合作需要时间为：500/（2+3）=100天；

则该工程产生的费用为：

1.5x（50+100）+3x100=525，答案选C。

例3：某浇水装置可根据天气阴晴调节浇水量，晴天浇水量为阴雨天的2.5 倍。灌满该装置的水箱后，在连续晴天的情况下可为植物自动浇水 18 天。小李 6 月 1 日 0：00 灌满水箱后，7 月 1 日 0：00 正好用完。

问 6 月有多少个阴雨天？（ ）

A．10 B．16 C．18 D．20

解析： 题干出现时间和工作效率之比，考虑赋值工作效率；

根据“晴天浇水量为阴雨天的2.5倍”，赋值阴雨天的浇水量为2，晴天浇水量为5；

则有工作总量为：18x5=90；

6月共有30天，假设阴雨天为x，则有晴天为30-x天；

则有工作总量为：

2x+5（30-x）=90，化简为：150-3x=90，x=20；

答案选D。

例4：甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5:4:6 。先由甲、乙两人合做 6 天，再由乙单独做 9 天，完成全部工程的 60%。若剩下的工程由丙单独完成，则丙所需要的天数是（ ）。

A.9 B.11 C.10 D.15

解析： 题干中出现工作效率之比，考虑赋值工作效率；

将效率之比直接视为工作效率，则甲、乙、丙的工作效率分别为：5、4、6；

则有：

【6x（5+4）+4x9】／60%=工作总量；

工作总量x40%=剩余工作量；

剩余工作量／6=丙所需要的天数；

即：

例5：某件刺绣产品，需要效率相当的三名绣工8 天才能完成；绣品完成50%时，一人有事提前离开，绣品由剩下的两人继续完成；绣品完成 75%时，又有一人离开，绣品由最后剩下的那个人做完。

那么，完成该件绣品一共用了（）天。

A．10 天 B．11 天 C．12 天 D．13 天

解析： 题干中出现工作效率和工作时间，考虑赋值工作效率，求得工作总量；

由于三名绣工效率相当，考虑每人的效率都为1，

则工作总量为3x8=24；

绣品完成50%，即12，耗费工作时间为4天；

绣品完成75%，即18，其中由2个人完成的工作量为6，工作效率为2，耗费工作时间为3天；

剩余工作量为25%，即6，工作效率为1，耗费工作时间为6天；

故完成该绣品共需：4+3+6=13天，答案选D。

以上就是工程问题，从核心公式出发，明确给定不同条件的情况下的最佳解题方法；

在此基础上，不要忘记有关数字特性的内容，不要忘记万能的方程，多多去练题，提高对于特定概念，特定题型和数字的敏感性，快狠准的拿分！

数量关系 5.高频考点常用解题方法-利润问题

利润问题

利润问题非常容易识别，涉及到成本、售价、盈利、折扣等与金钱有关的题目即为利润问题。

●在利润问题的考查中常涉及到如下名词：

成本：进价、支出、其他成本；

售价：原售价、定价；

利润：盈利、收益；

折扣：实际售价与原定价之间的比例关系，

折=实际售价／原定价；

如：打三折，即实际售价=原定价x30%；

折扣率：折扣与原定价之间的比例关系，

折扣率=1-折扣；

利润率：利润与成本之间的比例关系，

即利润率=利润／成本。

●核心公式拓展公式：

售价=成本+利润；

售价=原定价x折扣；

总成本／总利润／总销售额=单个成本／单个利润／单个销售额x数量；

期望利润=原定价-成本；

实际利润=售价-成本。

●常考查题型：

(1)一般利润问题

即考查成本、售价、利润、折扣、折扣率等问题；

(2)分批销售问题

因销售过程中出现售价、折扣、销售量等的调整，致使一个销售过程中出现的不同的售价、折扣、利润和数量的组合；

相较于一般利润问题而言，分批销售稍显复杂，但只要抓住一条主线，总=部分之和；

即：

总销售收入=第一部分销售收入+第二部分销售收入；

总利润=第一部分销售利润+第二部分销售利润；

总销售量=第一部分销售量+第二部分销售量；

...

或根据题干给定的等量关系列式，很容易求得答案。

(3)分段计价问题

常涉及水电费燃气费、奖金提成、出租车计价等资费问题，重点和关键在于找准分段的节点，分不同的区间计算费用。

●常用解题方法：

(1)方程法：

利润问题中涉及的概念较多，考法也较多样；

尽管如此，但是却很容易能找到等量关系；

利用等量关系列方程对于利润问题的求解是最直观最稳妥的；

(2)赋值法：

但在方程法的基础上，也常用到赋值法；

什么时候用到？在题干中只给定的比例关系时～

明确了以上，我们一起来看例题。

例1：超市采购一批食用油，其中玉米油每桶进价比花生油低20％，若花生油利润定为进价的 24％，玉米油利润定为进价的 30％，则花生油比玉米油每桶售价高 10 元。

问玉米油每桶比花生油进价低多少元？

A.10 B.15 C.24 D.25

解析： 题干出现百分数，即出现比例关系；

在假设未知数时，要注意根据比例关系尽量将未知数设为好算的数字；

翻译比例关系：

例2：某产品售价为67.1 元，在采用新技术生产节约 10%成本之后，售价不变，利润可比原来翻一番。则该产品最初的成本为______元。

A.51.2 B.54.9 C.61 D.62.5

解析：题干出现百分数，即比例关系；

考虑假设最初成本为10x，则采用新技术节约成本x，现成本为9x；

列式为：

67.1-9x=2（67.1-10x）

整理方程则有：

67.1=11x，x=6.1

则最初成本10x=61，答案选C。

例3：商店采购了一种水果，第一天在进货成本基础上加价40%销售，从第二天开始，每天的销售价格都比前一天低 10%。已知第三天这种水果的售价比第一天降低了 13.3元/千克。

问这种水果的进货成本为多少元/千克？

A.35 B.40 C.45 D.50

解析： 题干出现百分数，且出现了不同的售价，即考查分批销售；

考虑根据百分数的比例关系假设未知数；

假设水果进货成本为5x，则第一天售价为5x（1+40%）=7x；

第二天比第一天低10%，即低0.7x,售价为6.3x；

第三天比第二天低10%，即低0.63x；

根据等量关系列式有：

0.7x+0.63x=1.33x=13.3，则x=10；

进货成本为5x=50，答案选D。

例4：某商场开展购物优惠活动：一次购买300 元及以下的商品九折优惠；一次购买超过 300 元的商品，其中 300 元九折优惠，超过 300 元的部分八折优惠。小王购物第一次付款 144 元，第二次又付款 310 元。

如果他—次购买并付款，可以节省多少元？（ ）

A. 16 B. 22.4 C. 30.6 D. 48

解析： 题干出现分段计价，务必找准分段节点；

根据题意，活动分为2个区间：

未超过300的部分，折扣为9折；

若正好为300，则需支付300x0.9=270；

超过300的部分，折扣为8折；即可推知，若支付总价超过270，则原价一定超过300元。

小王第一次付款144元，低于270，可知在第一区间，原价为144/0.9=160元；

第二次付款310元，超过270元，可知超过300元的部分为：（310-270）／0.8=40/0.8=50元；

故若一次购买并付款，总价为160+300+50=510元；

需实际支付：

270+210x0.8=270+168=438；

可节省144+310-438，尾数应为6，答案选A。

例5：小王从甲公司跳槽到乙公司，年工资总额增长25%，乙公司的工资总额包括现金部分和股票部分，现金总额和股票价值总额比例为 3:1，股票价值按照签订合同当日股票收盘价计算。一年后公司由于重大变动股价比小王入职时下跌 48%，如果按此时股价计算，小王在乙公司工作一年获得的实际工资总额与在甲公司相比：

A.下降 10% B.下降 15% C.增长 10% D.增长 15%

解析： 题干中只出现了比例关系，同时选项亦为比例关系，考虑为题干中的变量赋值；

翻译比例关系：

以上就是利润问题；

熟知名词概念，记住核心公式，明确等量关系，根据不同的条件利用方程法或赋值法，求得相应答案；

多多去练题，提高对于特定概念，特定题型和数字的敏感性，快狠准的拿分！

数量关系6. 高频考点常用解题方法-行程问题

行程问题

行程问题是数量关系考查的重点题型之一，几乎年年考，卷卷考～～

考的频率高，考查的方式也多变，总体来说，难度稍大；

但形式虽多，也依然可以被整理被总结：

1.题型特征：涉及路程、速度和时间的关系；

2.常考查的题型：

一般行程问题、相遇追及问题、直线单端or两端出发相遇问题、环形相遇追及问题、流水行船、过桥、等距离平均速度等其他行程问题。

行程问题核心公式：

我们说但凡是行程问题，无论题型如何变形考查，其涉及的变量都是路程、速度和时间；

三者之间形成如下等量关系：

路程=速度x时间，即：s=vt，这也就是行程问题的核心公式。

●一般行程问题

故对于一般行程问题，只要找对了数据或比例关系，根据核心公式，即可找到答案；

单位换算：

需要注意的是：

一般行程问题中，常出现单位的换算，即：

千米／时（km／h）和米／秒（m／s），甚至米／分钟（m/min）之间的换算关系；

如何换算呢？

举个例子：

而米／秒和米／分钟之间就简单很多，从秒变分，乘以60即可；从分变秒，除以60即可。

●相遇追及问题：

(1)相遇问题

即：两个人、物从两地同时出发，面对面相向而行，经过一段时间，二者必然在途中相遇；

即有：相遇距离=速度和x相遇时间；

(2)追及问题

即：两个人、物同时出发同向而行，一个速度快，一个速度慢；当速度慢的走在前，经过一段时间，速度快者必然会追上速度慢者；

即有：追及距离=速度差x追及时间。

理解过程，记住结论，读清题干，可画图模拟整个过程；

现在一起来看例题咯。

例1：甲、乙两人从湖边某处同时出发，沿两条环湖路各自匀速行走。甲恰好用2 小时回出发点，比乙晚到 20 分钟，多走了 2800 米。若甲每分钟比乙多走 10 米，则甲行走的速度是：

A.4.2 千米/小时 B.4.5 千米/小时 C.4.8 千米/小时 D.5.4 千米/小时

解析：

根据题干，甲乙两人走不同的路，给定了甲乙走完全程的时间、速度差和路程差，求速度；

假设甲的速度为v，则乙的速度为v-10，单位为米／分钟；

根据题干条件可知：

甲走完自己的路用时120分钟，乙走完自己的路用时100分钟；

列式有： 120v-100(v-10)=2800,

整理可得：

20v=1800，v=90米／分钟，单位为米／分，从小变大，需要乘以0.06，即甲的速度为：

v=90x0.06=5.4千米／小时，答案选D。

例2：小赵骑车去医院看病，父亲在发现小赵忘带医保卡时以60 千米/小时的速度开车追上小赵，把医保卡交给他并立即返回。小赵拿到医保卡后又骑了 10 分钟到达医院，小赵父亲也同时到家。假如小赵从家到医院共用时 50 分钟，则小赵的速度为多少千米/小时？（假定小赵及其父亲全程都匀速行驶，忽略父子二人交接卡的时间）

A．10 B．12 C．15 D．20

解析：

题干出现追及关键词，辅助画图来理清整个过程：

根据题干条件：

赵父从红色虚线处返回家用时=小赵从红线虚线处到达医院用时=10min；

同样的路程，小赵用时50-10=40分钟；

路程一定的情况下，速度和时间成反比，则有：

赵速度：赵父=1:4，

可知小赵速度为60/4=15，答案选C。

例3：甲从邮局出发去图书馆，乙从图书馆出发去邮局。两人12 点同时出 发，相向而行。12 点 40 分两人相遇并继续以原速度前行。13 点 12 分甲到达图书馆后立刻返回邮局。假定 两人速度不变，甲返回邮局时，乙已到邮局多长时间了？

A.40 分钟 B.50 分钟 C.54 分钟 D.64 分钟

解析：

题干出现相遇问题，辅助画图来理清整个过程：

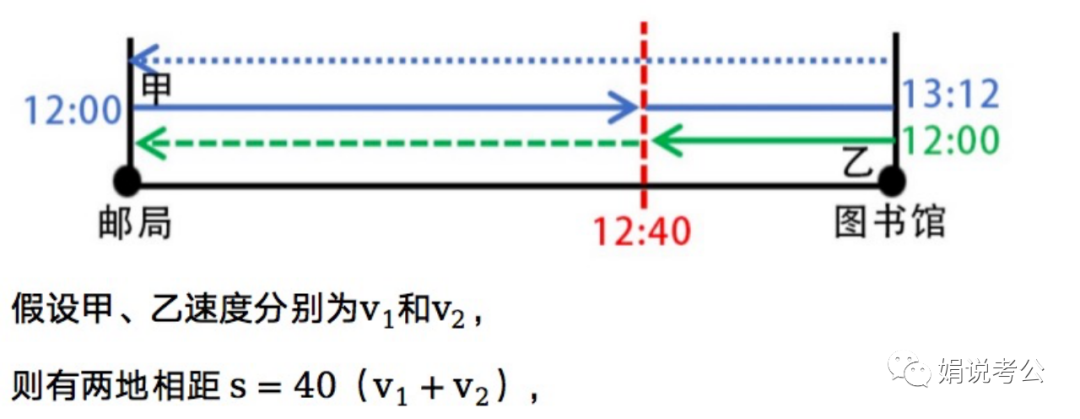
根据条件和图示可知：

红色虚线到图书馆之间的距离是乙花40分钟走过的，也是甲花32分钟走过的；

可知，路程一定的情况下，时间和速度成反比：

且有甲走完单程用时为72分钟，则乙走完单程需要：

72/4x5=90分钟，

而甲从邮局到图书馆，再返回邮局共用时：2x72=144分钟；

相差144-90=54分钟；

答案选C。

通过例2和例3，我们可以看出画图的重要性，题干中虽然提到了“追”、“相遇”，但整个解题过程并未涉及到相遇追及问题的距离公式，而是仅仅围绕核心公式：路程=速度x时间，及三者之间的比例关系，快速求得答案；

所以提醒大家，不要偏离核心，核心永远是最重要的。

毕竟即便是我们的相遇追及公式，也是从核心公式出发，通过画图辅助推导而得出的，不是么？

例4：甲、乙各自驾驶汽车匀速相向行驶，且同时进入双向公路隧道的两端，30 秒后两车相遇。甲车继续行驶 20 秒到达隧道出口时，乙车距离出口还有 200 米。问隧道的长度为多少米？

A.450 B.500 C.600 D.800

解析：

题干出现相遇问题，辅助画图来理清整个过程：

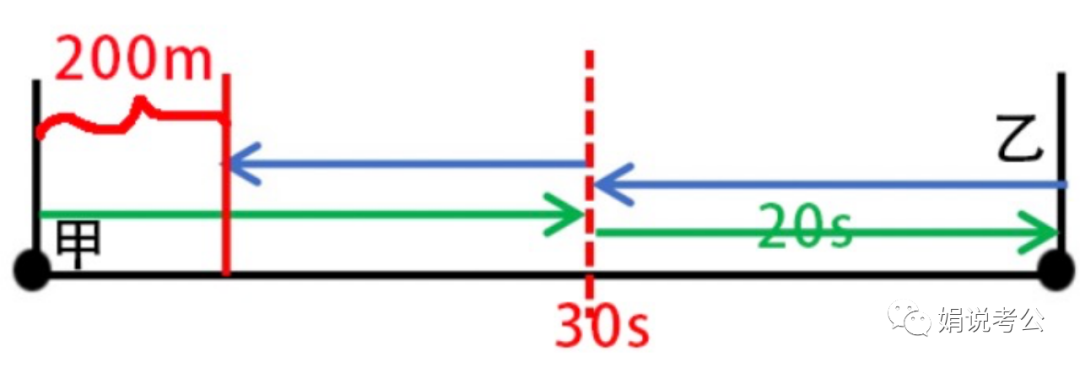
由题干条件可知：

从红色虚线到右侧的距离，甲用时20s，乙用时30s；

路程一定的情况下，速度和时间成反比，可知：

甲速度：乙速度=3:2，假设乙速度为2v，则甲速度为3v；

则有：50x2v+200=50x3v，则v=4，

隧道总长度为50x3x4=600米，答案选C。

例5：某清晨，爷爷、爸爸和小磊在同一条笔直跑道上朝同一方向匀速晨跑，某一时刻，爷爷在前，爸爸在中，小磊在后，且三人之间的间距正好相等。跑了12 分钟后小磊追上了爸爸，又跑了 6 分钟后小磊追上了爷爷，则再过（ ）分钟，爸爸可追上爷爷。

A.12 B.15 C.18 D.36

解析：

题干中出现追及问题，考虑利用追及距离公式：

假设“某一时刻”，三人之间的间距为s，即爷爷和爸爸间距为s，爸爸与小磊间距为s，爷爷与小磊间距为2s；

假设三人的速度分别为：

以上是行程问题中的一般行程问题和相遇追及问题；

在核心公式的基础上，画图辅助理清整个过程，找准比例关系或等量关系，快狠准找到答案。

●直线型单端出发n次相遇问题：

拆解一下：

直线、单端出发、n次相遇：

要同时满足这3个条件，必然是速度一快一慢，快的返回途中和慢的相遇，相遇后继续出发，再返回再次相遇;

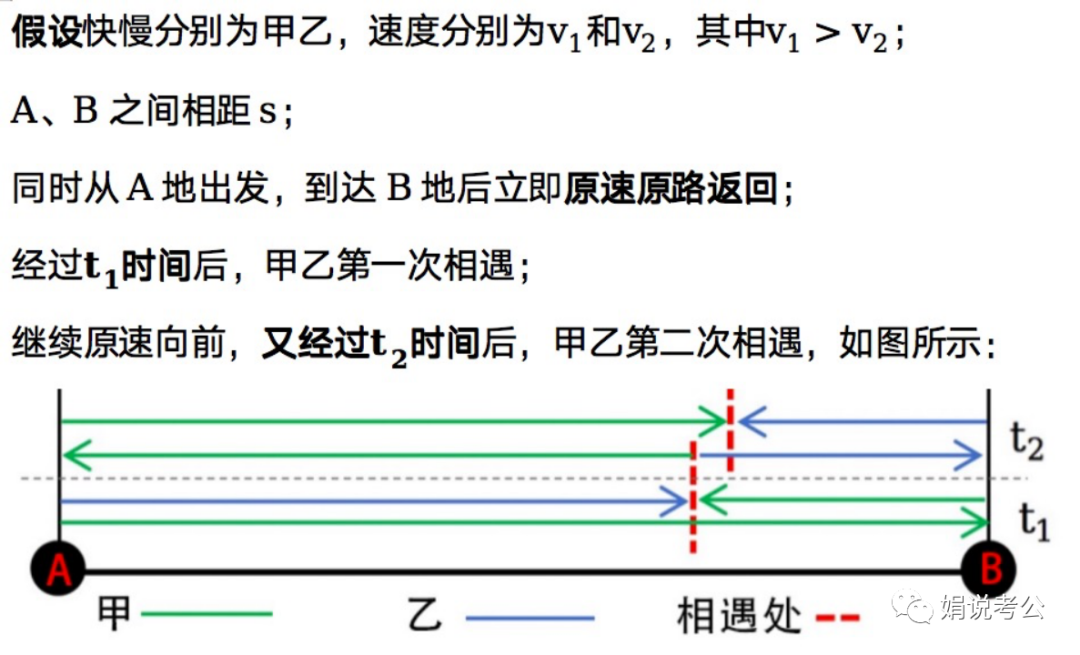
且有：每一次相遇甲和乙走过的距离都与上一次相遇走过的距离相同，为什么？

因为路程=速度x时间呐；

甲一直匀速，那相同的时间一定走出相同的距离；乙亦如是。

●直线型两端出发n次相遇问题

两端出发与单端出发的区别在哪里？

就是少了一个快的超过慢的然后返回才能相遇的过程，两端出发中，相向而行第一次相遇，返回途中或者返回又返回的途中再次相遇，然后一直循环下去～

且有：从每二次起，每一次相遇甲和乙走过的距离都与上一次相遇走过的距离相同，为什么？

因为路程=速度x时间呐；

甲一直匀速，那相同的时间一定走出相同的距离；乙亦如是。

且第一次相遇时二者分别走过的距离为其他次相遇时二者分别走过距离的一半！

为什么？

依然因为路程=速度x时间！

理解了么？一起来看例题醒醒脑呐～

例1：小张、小王二人同时从甲地出发，驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快，两人出发后第一次和第二次相遇都在同一地点，那么小张的车速是小王的（ ）倍。

A．1.5 B．2 C．2.5 D．3

解析：

根据题干，两人同时同向出发往返行驶，即直线单端出发相遇问题；

根据题意，辅助画图理清整个过程：

根据单端出发的理论，两次相遇用时t是一样的，

每次相遇小张走过的路程相同，小王走过的路程相同；

根据图示可知，第二次相遇小张走过的路是第一次相遇小王走过的路的2倍；

根据路程时间和速度之间的比例关系；

在时间一定的情况下，路程与速度成正比，可知小张的速度是小王的2倍，答案选B。

例2：甲、乙两人在长30 米的泳池内游泳，甲每分钟游 37.5 米，乙每分钟游 52.5米。两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。如果不计转向的时间，则从出发开始计算的 1 分 50 秒内两人共相遇了多少次？（ ）

A．2 B．3 C．4 D．5

解析：

根据题干，甲乙二人从直线两端出发往返，即直线两端出发n次相遇问题；

根据结论：

相遇距离=速度和x相遇时间=（2n-1）s；

则1分50秒内，两人游过的距离和为：

例3：甲从A 地，乙从 B 地同时以均匀的速度相向而行，第一次相遇离 A 地 6 千米，继续前进，到达对方起点后立即返回，在离 B 地 3 千米处第二次相遇，则 A、B 两地相距多少千米？

A.10 B. 12 C. 18 D. 15

解析：

根据题干，甲乙从两地出发相向而行往返，即直线两端出发n次相遇问题；

根据结论，即有：

相遇距离=（2n-1）s=速度和x相遇时间；

但题目中没有给有关速度的条件，辅助画图来理清一下整个过程：

前面我们说，

在两端相遇问题中，第一次相遇时间为t，则第一次到第二次相遇经过的时间为2t；

根据图示可知：

甲从出发至第一次相遇所走过的路程6km，则甲从第一次相遇到第二次相遇之间所走过的距离应为12km；

可推知：两条红色虚线之间的距离为：12-2x3=6；

则A、B两地相距应为6+6+3=15km，答案选D。

以上是行程问题中的直线n次相遇问题；

理解过程中的走向，根据核心公式及路程、速度、时间三者之间的比例关系，尝试去画图，去推导，去分析整个过程；不用每次都分析，甚至只需要分析一次，带你的脑细胞去体验一下整个过程，就一定会印象深刻的；

行程问题中的环形n次相遇追及问题；

●环形n次相遇问题：

我们将熟悉的直线型相遇问题转化为环形相遇，即将直线两端连接起来变成环形，如下图所示：

假设二者为甲乙，同时从黑点处向相反的方向出发；

很显然，甲乙第一次相遇时走过的路程和为一个周长；

如果继续原速向前，下一次遇见的时候二者又一起走了一圈；

即：

第一次相遇的相遇路程为周长；

第一次相遇到第二次相遇又走过一个周长，从出发到第二次相遇共2个周长；

同样，从出发到第三次相遇共走过3个周长；

...

可推知，从出发到相遇n次，共走过的路程为n个周长；

即有：

同时同地出发，相遇距离=n周长=速度和x相遇时间。

那如果并非从同一个地点出发，会是什么情况？

依然看图示：

甲乙二人同时分别从A、B向相反的方向出发，则第一次相遇时走过的路程和为周长减去A、B之间的距离AB；

相遇之后继续原速出发，下一次遇见的时候二者一起走了一圈；

即：

第一次相遇的相遇路程为周长-AB；

第一次相遇到第二次相遇走过一个周长，从出发到第二次相遇共2个周长-AB；

同样，从出发到第三次相遇共走过3个周长-AB；

...

可推知，从出发到相遇n次，共走过的路程为n个周长-AB；

即有：

同时同地出发，相遇距离=n周长-AB=速度和x相遇时间。

●再来看环形n次追及问题：

我们依然用熟悉的直线型追及问题来转化为环形追及，即将直线两端连接起来变成环形，则同样存在两种情况，一种是同时同地出发，一种是同时异地出发，分别来看；

同时同地出发图示如下：

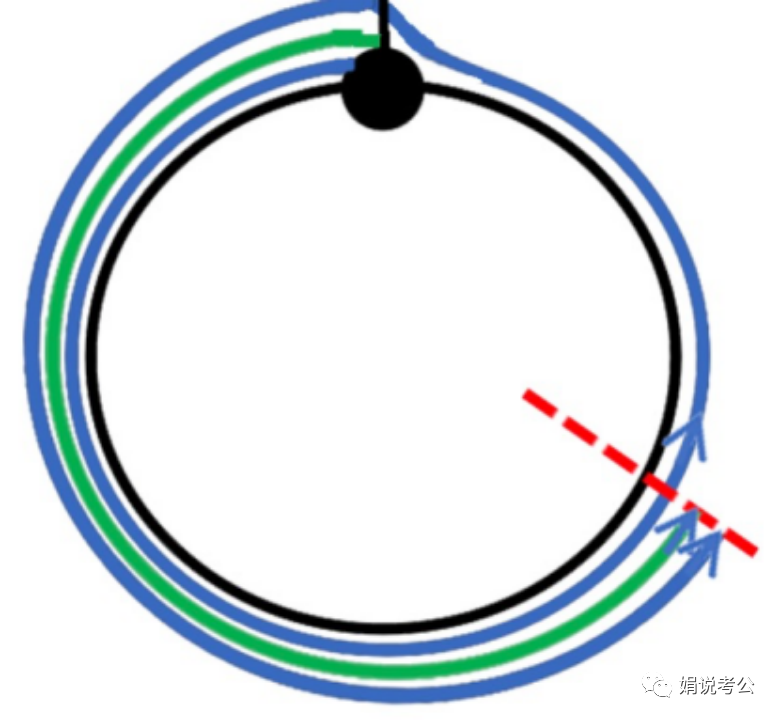
甲乙从同一起点同向出发，甲速度比乙快，则在甲走第一圈并不能与乙相遇，甲走第二圈的过程中会追上乙；此时，甲比乙多走出了一圈的距离；

则有：

甲第一次追上乙，追及距离为一个周长；

甲乙继续原速出发，相当于二者又从同一起点同时出发，甲再次追上乙时，又追及了一个周长；

...

可知，同时同地出发时，甲追上n次乙，追及距离为n个周长；

即有：

同时同地出发，追及距离=n周长=速度差x追及时间；

那如果是异地出发呢？图示如下：

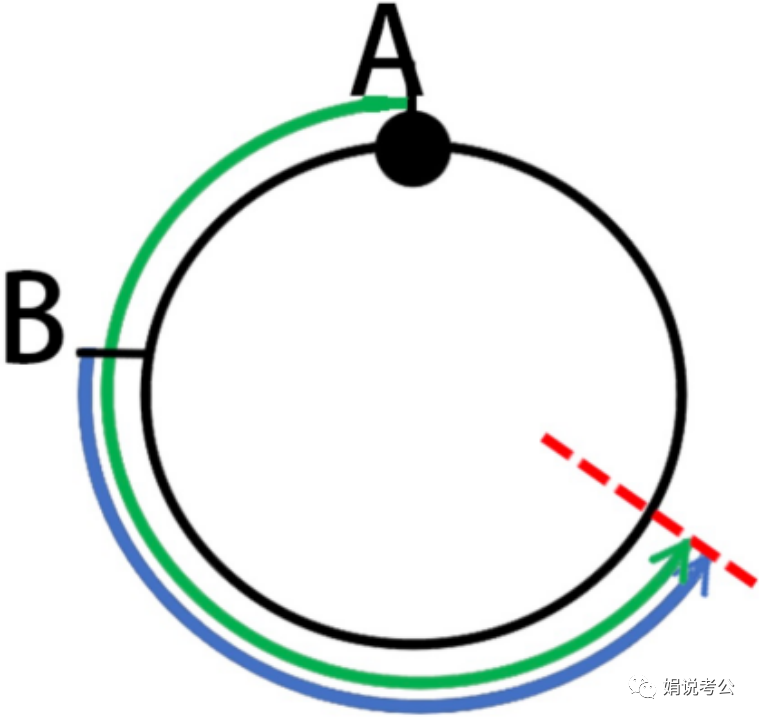
甲从A点出发，乙从B点出发，甲的速度比乙快，则第一次追上乙时，追及距离为：

速度差x追及时间=AB（AB两点之间的距离）；

继续原速出发，即此时甲乙从同一个起点同时出发，那再次追上是，甲又追及的距离为一个周长；

...

以此类推：

可知，同时异地出发，甲追上乙n次，追及距离=n周长+AB。

理解了么？

一起来看例题醒醒脑呐～

例1：甲、乙、丙、丁四人同时同地出发，沿一椭圆形环湖栈道行走。甲顺时针行走，其余三人逆时针行走，已知乙的行走速度为60 米/分钟，丙的速度为 48 米/分钟，甲在出发 6、7、8 分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少？（ ）

A．31 米/分钟 B．36 米/分钟 C．39 米/分钟 D．42 米/分钟

解析：

根据题干，四个人同时同地走同一个环形，甲分别与乙、丙、丁相遇；

考查环形相遇问题；

可知，甲与每个人相遇时，该两人走过的路程和为一个周长；

题干中已知了乙和丙的速度，假设甲的速度为a，丁的速度为b，根据题干条件有：

6(a+60)=7(a+48),

则有：a=360-7x48=360-336=24；

又：8(a+b)=8(24+b)=6x84,

则有：

24+b=3x21，则b=63-24=39，答案选C。

例2：老林和小陈绕着周长为720 米的小花园匀速散步，小陈比老林速度快。若两人同时从某一起点同向出发，则每隔 18 分钟相遇一次；若两人同时从某一起点相反方向出发，则每隔 6 分钟相遇一次。由此可知，小陈绕小花园散步一圈需要多少分钟？

A．6 B．9 C．15 D．18

解析：

题干已知周长、相遇和追及时间，假设小陈和老林的速度分别为a和b，

根据环形相遇和追及公式，即有：

18(a-b)=6(a+b)=720

易求得，a=80，b=40；

则小陈绕一圈时间为720/80=9，答案选B。

例3：如图，在长方形的跑道上，甲、乙两人分别从A 处和 C 处同时出发，均按顺时针方向沿跑道匀速奔跑。已知甲的速度为 5 米/秒，且甲第一次追上乙时，甲恰好跑了 5圈回到 A 处，则乙的速度为（ ）。

A. 4.8 米/秒 B. 4.5 米/秒 C. 4 米/秒 D. 5 米/秒

解析：

根据题干可知，甲乙二人同时异地出发，考查环形异地追及问题；

假设乙的速度为a，则有：

甲第一次追上乙时，追及的距离为甲乙起点之间的距离，即：20+12=32；

且甲用时为5x64（周长）／5=64秒；

根据追及公式：追及距离=速度差x时间，

则有：

32=64x(5-a)，求得a=4.5，答案选B。

例4：一条圆形跑道长500 米，甲、乙两人从不同起点同时出发，均沿顺时针方向匀速跑步。已知甲跑了 600 米后第一次追上乙，此后甲加速 20%继续前进，又跑了 1200 米后第二次追上 乙。

问甲出发后多少米第一次到达乙的出发点？

A. 180 B. 150 C. 120 D. 100

解析：

根据题意，甲乙同时异地出发，沿环形跑道追及；

根据环形追及公式：

第一次甲追上乙，追及距离为二者起点距离；

从第一次甲追上乙到第二次甲追上乙，追及距离为一个周长；

根据题干条件可知：

从第一次甲追上乙到第二次甲追上乙，甲跑的路程为1200米，乙跑的路程为1200-一个周长，即700米；

根据路程、速度和时间之间的比例关系，可知：

时间一定的情况下，速度和路程成正比，即甲乙速度之比为12:7；

为甲的速度赋值为12，乙的速度赋值为7；

则甲加速之前的速度为12/（1+20%）=10；

根据题干条件：

第一次甲追上乙时，甲跑了600米，可知用时为600/10=60，

则该追及时间内，乙跑的路程为7x60=420；

则追及距离=600-420=180；

答案选A。

以上是行程问题中的环形n次相遇、追及问题；

同直线型一样：

需要理解过程中的走向，尝试去分析整个过程，记住结论；

根据题干条件列方程或利用比例关系，即可快速求得答案。

●流水行船：

流水行船我们应该不陌生，甚至是很熟悉；

还记得公式是顺水=船速+水速，逆水=船速-水速；

没问题吧？

这里之所以存在加和减，是因为船速和水速相互作用，是典型的相对速度，相对于谁呢？

当然是相对于岸呐；

假设水速为0，是不是相对于岸来说，水是静止的？

那此时船在水中行驶，体现的就是真正的自己，水不帮忙也不捣乱，这叫静水行船；

那水不静止的时候，相对于岸来说，水是动的，速度就是水速；

假设此时船在水上，但是船自身速度为0，那相对于岸来说，船是动是静？

当然也是动的，水带着船走，走的速度=水速，这叫顺水漂流；

假设此时船动起来了，顺着水流的方向行驶，此时水顺推着船走，对船的行驶提供了帮助，这时的速度=船速+水速，这叫顺水行船；

那船突然掉头行驶，水怎么办？水也不能逆流而上，水依然按照自己的路线去走，对船的行驶就不再帮忙了，而是给了一个阻力，这是的速度=船速-水速，这叫逆水行船。

所以，在流水行船中，我们整理出现以下概念和公式：

理解过程，熟记公式，简单，很简单！

●过桥问题：

过桥问题与我们一般的行程问题的区别在哪里呢？

就是这个过桥指的是火车或者汽车，其车身有一定的长度，而这个“过桥”的“过”又解读为，从车头上到车尾下，所以必然就比一个人过桥多出了一个长度，我们用图示标明：

从图示可以看出，当具有一定长度的火车要过桥时，从车头上到车尾下，火车走过的路程为多少呢？

看车头：

从红色虚线到红色虚线，走过的路程为桥长+车身长；

看车尾：

从蓝色虚线到蓝色虚线，走过的路程为桥长+车身长。

得出结论：

过桥问题中，火车完全过桥走过的路程为桥长+车身长；

那完全过桥是从车头上到车尾下，那假设从一开始火车就在桥上了呢？

依然盯着头或尾，如果一开始火车在桥上，车尾在桥一端，那火车完全下桥，则走过的路程为桥长；

如果火车没有完全下桥，而是车头走到桥另一端就停了，那走过的距离就是桥长-车身长。

●等距离平均速度：

什么是等距离平均速度呢？

顾名思义，就是用不同的速度走过相等的距离，求该过程的平均速度；

常见的等距离有：往返、上坡下坡等；

举个例子：

小明出门去公园，匀速走到公园，速度为a；返回时匀速跑回家，速度为b；若求小明往返公园的平均速度为多少？

这怎么求？没有时间没有路程的？

以上就是流水行船、过桥和等距离平均速度了，理解了么？

一起来看例题～

例1：某公路铁路两用桥，一列动车和一辆轿车均保持匀速行驶，动车过桥只需35秒，而轿车过桥的时间是动车的 3 倍，已知该动车的速度是每秒 70 米，轿车的速度是每秒21 米，这列动车的车身长是（轿车车身长忽略不计）

A．120 米 B．122.5 米 C．240 米 D．245 米

解析：

根据题干，已知过桥时间和速度，求动车车身长，即过桥问题；

假设桥长为x，动车车身长为y，则有：

35x70=x+y；

3x35x21=x；

则有y=35x70-35x3x21=35x7=245，答案选D。

例2：一艘轮船先顺水航行40 千米，再逆水航行 24 千米，共用了 8 小时。若该船先逆水航行 20 千米，再顺水航行 60 千米，也用了 8 小时。

则在静水中这艘船每小时航行（）千米。

A．11 B．12 C．13 D．14

解析：

题干已知顺水和逆水，求静水中速度，即求船速，可先求出顺水和逆水速度；

假设顺水速度为a，逆水速度为b，根据题干条件则有：

例3：某旅游部门规划一条从甲景点到乙景点的旅游线路，经测试，旅游船从甲到乙顺水匀速行驶需3 小时；从乙返回甲逆水匀速行驶需 4 小时。假设水流速度恒定，甲、乙之间的距离为y公里，旅游船在静水中匀速行驶y公里需要x小时，则x满足的方程为（ ）。

解析：

根据题干，已知逆水行驶时间和顺水行驶时间，并给定了未知数路程和船速，

到这里有同学可能没看出来在考查什么，我们来分析下：

设问问满足的方程；

方程是什么？是一个等量关系，那题干中能找到什么等量关系是与给定条件和未知数有关的？

只有水速了！

所以，其实就是在考查顺水、逆水、船速和水速之间的等量关系；

我们知道船速+水速=顺水速度，船速-水速=逆水速度；

可知水速=顺水速度-船速=船速-逆水速度。

根据题干条件列式：

例4：从甲地到乙地111 千米，其中有 1/4 是平路，1/2 是上坡路，1/4 是下坡路。假定一辆车在平路的速度是 20 千米/小时，上坡的速度是 15 千米/小时，下坡的速度是 30 千米/小时。则该车由甲地到乙地往返一趟的平均速度是多少千米/小时？

A．19 B．20 C．21 D．22

解析：

根据题意，已知平路、上坡、下坡速度，求往返的平均速度；

看到平均速度，会想到我们的等距离平均速度，那这道题中有等距离么？

当然，去时的上坡路即为回时的下坡路，去时的下坡路即为回时的上坡路；

即往返中的上下坡对应为等距离；

可以试求上下坡路段的平均速度：

等距离平均速度=2速度积／速度和=2x15x30/45=20；

又平路的速度亦为20；

故全程往返的平均速度为20，答案选B。

有同学可能还没有理清楚，我们补个图示来看一下：

两个红色虚线框是两组等距离，由于上坡速度不变，下坡速度不变，故两个虚线框中的平均速度是一样的，都为同一个等距离平均速度；

理解了么？

以上是行程问题中的流水行船、过桥和等距离平均速度；

至此，我们的行程问题就介绍完了；

题型较多，但是理解了过程之后，会发现我们的解析都很简单，也就是这类题型基本上都可以简单列式或分析，秒出正确答案。