算法笔记-卡尔曼滤波器简单解释

本文为转载，原博客地址：http://blog.csdn.net/raym0ndkwan/article/details/50031729

算法笔记-卡尔曼滤波器简单解释

动态时间规整/规划(Kalman Filter, 又称linear quadratic estimation)也是一个比较老的算法，大概在1960年左右被提出来，算法的名字来自算法早期的一个提出者Rudolf E. Kálmán。卡尔曼滤波器至今还是十分常用的一种滤波算法，并且在此基础上发展出了很多种延伸的算法。卡尔曼滤波器算法的核心可由几道简洁的公式表示，但对于刚刚接触的人来说可能比较难以彻底理解这些公式，这篇笔记尝从一个实际的运动场景出发，具体解释卡尔曼滤波器的核心算法。

1.简介

卡尔曼滤波器在监控、导航和控制系统上有大量的运用。在这些系统里面，系统的观测量和这些被观测量的真实值往往是有细微差异的，基于我们对这些系统的认识（例如已有的描述系统的模型）和观测值，我们能够更好地推测系统的真实状态。这也是卡尔曼滤波器的核心思路，下面会先从公式出发，然后到一个简单的例子，进一步介绍这个思想是如何体现的。

2.公式

首先，假设一个系统在t时刻的状态是跟t-1时刻的状态是有关的：

xt=Ftxt−1+Btut+wt(1)

其中各项的意义如下： 
xt 是一个代表系统在t时刻的真实状态向量，该向量可以包含着例如位置，速度等信息； 
Ft 是t时刻的状态转换矩阵，代表着系统状态在t-1时刻对系统t时刻的影响，例如t-1时没有速度和加速度，那么在t时位置应该不变； 
ut 是t时刻的控制输入向量,例如是否有踩油门和转方向盘等； 
Bt 是t时刻的输入转换矩阵，即量化了输入对状态的影响； 
wt 是t时刻的过程噪声，我们假设该噪声服从均值为0的多变量正态分布，其协方差矩阵我们标记为 Qt 。

然后，我们要留意到，我们观察或测量的值往往不能直接反应我们关心的状态值，而且测量也存在测量误差，我们用下面这一式子反应这些： 

zt=Htxt+vt(2)

其中各项的意义如下： 
zt 代表系统在t时刻的观察值向量，该向量包含着系统测量的结果； 
Ht 是t时刻的测量转换矩阵，这个矩阵表示状态向量和观察值向量之间的关系，当观察值就是状态时，该矩阵为单位矩阵； 
vt 是t时刻的测量误差，类似过程噪声，我们假设该误差服从均值为0的多变量正态分布，其协方差矩阵我们标记为 Rt 。

卡尔曼滤波器要解决的问题，或者说将式子(1)和(2)简单概括一下，就是已知 Ft ， ut ， Bt ， zt ， Ht ， xt−1 并且 wt 与 vt 服从已知的正态分布1，求解 xt 。 
我们首先假设所求状态服从一个多变量的正太分布,即 x∼N(μ,Σ) 。然后卡尔曼滤波器是通过一个迭代的过程解决这个问题的，每一次迭代包含两步，分别是预测和观测两步。

第一步预测：

x^t|t−1=Ftx^t−1|t−1+Btut(3)

Pt|t−1=FtPt−1|t−1FTt+Qt(4)

此处出现的几个新的项： 
首先是带帽的状态量 x^ ，主要用于与真实值区分开，这个值是卡尔曼滤波器的运算结果，即我们的对状态量的估计值。从另一个角度讲，这个就是我们估测的 μ 。 
而 P 是一个协方差矩阵，也就是我们估计的 Σ 。 
其中 t|t−1 指的是 t 时刻的预测步的结果，而 t−1|t−1 指的是 t−1 时刻的观测步的结果。

第二步观测： 

x^t|t=x^t|t−1+Kt(zt−Htx^t|t−1)(5)

Pt|t=Pt|t−1−KtHtPt|t−1(6)

其中 Kt 是卡尔曼增益： 

Kt=Pt|t−1HTt(HtPt|t−1HTt+Rt)−1(7)

以上就是卡尔曼滤波器的核心公式（式子(3)至式子(7)），注意，尽管对于标量问题也适用，这里讨论的变量大多是向量或者矩阵，而非标量。简单说来就是，每一次迭代分两步，在预测步状态(可用一个正态分布描述)的均值和协方差根据系统的模型更新，在观察步状态的均值和协方差根据观察值更新。

3.例子

光看公式可能会比较难以理解，我们现在考虑一个具体的例子。

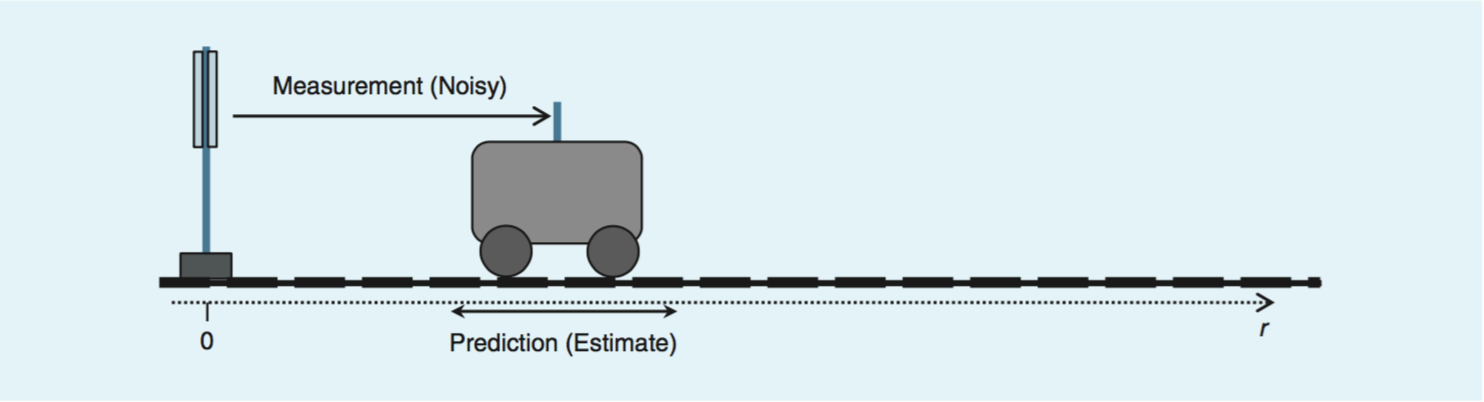
假设一辆列车在一维的铁轨上运动，如上图。假设我们关心的是列车相对于0点的位置和其速度，那么 xt 可以表示为： 

xt=[xtx˙t]

其中 xt 为位置， x˙t w为速度。

假设 t 时刻，我们已知火车的推进力为 ft 且火车的质量为 m ，那么控制输入向量为：

ut=ftm

同时，用 Δt 表示 t 时刻与 t−1 时刻间的时间差，由经典力学(对于这个系统的模型)我们可以知道：

xt=xt−1+(x˙t−1×Δt)+ft(Δt)22m

x˙t=x˙t−1+ftΔtm

以上只是简单的标量物理运算，我们可以整理为矩阵的形式：

[xtx˙t]=[10Δ11][xt−1x˙t−1]+⎡⎣⎢(Δt)22Δt⎤⎦⎥

将上式与式子(3)比较，可以看到: 

Ft=[10Δ11]

Bt=⎡⎣⎢(Δt)22Δt⎤⎦⎥

式子(3)实际上就表达了以上过程，所以式子(3)并没有什么神奇，只是基于系统模型的状态的均值的更新。但是，跟式子(1)相比，我们忽略了过程噪声项，因为这个会在式子(4)里面有所体现。式子(4)更新了协方差，协方差代表着我们对我们当前的预测的信心。

按照定义，协方差是：

Pt|t−1=E[(xt−x^t|t−1)(xt−x^t|t−1)T]

上式中E代表求均值运算。对比式子(3)和式子(1)，我们有： 

xt−x^t|t−1=Ft(xt−1−x^t−1|t−1)+wt

将上式代入协方差的定义中：

Pt|t−1=E[(Ft(xt−1−x^t−1|t−1)+wt)(Ft(xt−1−x^t−1|t−1)+wt)T]

并化简，得：

Pt|t−1=FtE[(xt−1−x^t−1|t−1)×(xt−1−x^t−1|t−1)T]FTt+FtE[(xt−1−x^t−1|t−1)wTt]+E[wt(xt−1−x^t−1|t−1)T]FTt+E[wtwTt]

这里面有四项均值，由于过程噪声和状态预估误差不相关，所以其中两项为0：

E[(xt−1−x^t−1|t−1)wTt]=E[(wt(xt−1−x^t−1|t−1)T]=0

又因为 E[wtwTt] 实际上是过程误差的协方差的定义，所以上式可以被进一步化简为：

Pt|t−1=FtE[(xt−1−x^t−1|t−1)×(xt−1−x^t−1|t−1)T]FTt+Qt

上式即是式子(4)。

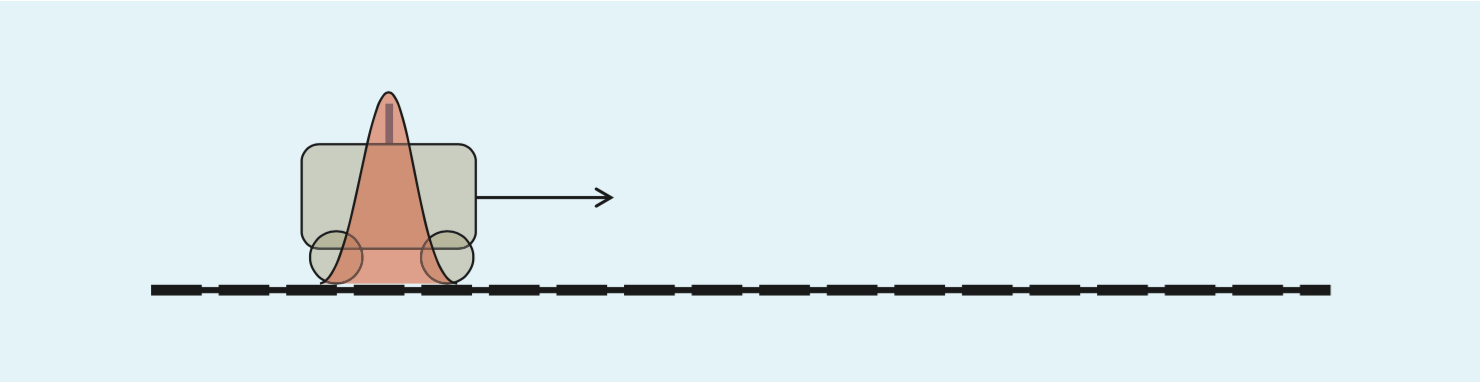
如果只有这一步，而没有第二步(即没有实时测量数据)，那么我们对状态预估的信息也会下降（因为有过程噪声）。如下两图所示，其中红色的分布代表着我们预测的位置的分布，在火车运行一段时间后，我们对其位置估测会更加分散扁平在均值的周围。

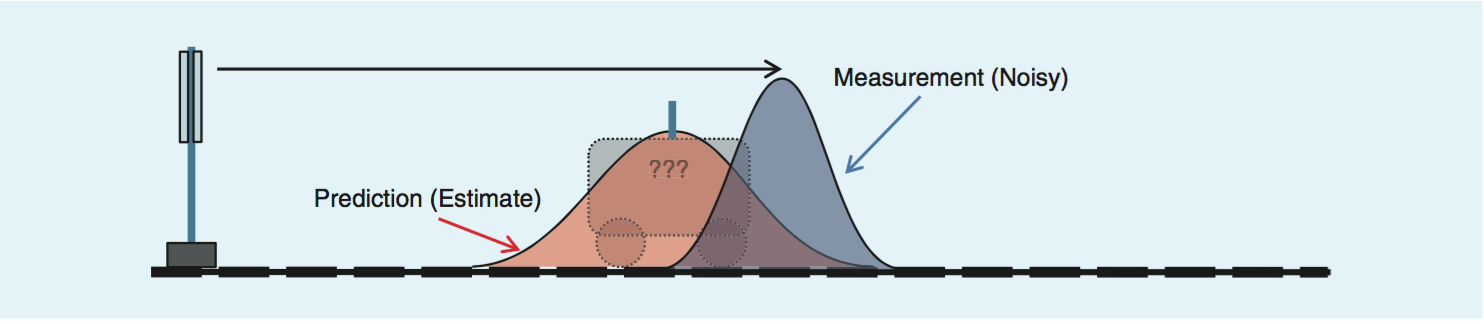
要使用卡尔曼滤波器，必须得有观测输入，例如下图： 

假设给定两个序列，样本序列 X=(x1,...,xN) 和测试序列 Y=(y1,...,yN) ，同时给定一个序列中点到点的距离函数 d(i,j)=f(xi,yj)≥0 (一般为欧氏距离，实际上也可以是别的函数)。蓝色的分布表示着我们用激光测距仪测出的列车的位置，同时它的扁平程度也代表了我们对测量结果的信心。

卡尔曼滤波器的测量步实际上把上图的两个分布结合起来，换句话说，将观测值和预测值结合起来才是一个更好的结果。由于预测和测量都服从正态分布，卡尔曼滤波器可以进一步利用这一点。下面用位置状态作为例子来解释算法的观测步的式子(5)(6)(7)。

如果我们只考虑位置而不考虑速度，将预测和测量正太分布的相乘，仍然会得到正太分布。例如 xp 代表着图中红色的预测， xm 代表着图中蓝色的观测，那么我们有：

xp(r;μ1,σ1)=12πσ21−−−−√e−(r−μ1)22σ21

xm(r;μ2,σ2)=12πσ22−−−−√e−(r−μ2)22σ22

将两者融合：

xfused(r;μ1,σ1,μ2,σ2)=12πσ21−−−−√e−(r−μ1)22σ21×12πσ22−−−−√e−(r−μ2)22σ22

=12πσ22σ21−−−−−−√e−((r−μ1)22σ21+(r−μ2)22σ22)

将其整理一下，可以看到：

xfused(r;μfused,σfused)=12πσ2fused−−−−−−−√e−(r−μfused)22σ2fused

且: 

μfused=μ1σ22+μ2σ21σ21+σ22

=μ1+σ21(μ2−μ1)σ21+σ22

又： 

σfused=σ21σ22σ21+σ22

=σ21−σ41σ21+σ22

下图绿色部分就是融合后的位置的分布： 

如果我们将融合后的分布的均值和方差与式子(5)(6)(7)对比，可以发现卡尔曼增益在这个例子里就是 σ21σ21+σ22 (此处测量的目标即为观测的状态所以测量转换矩阵为单位矩阵，可以忽略)。

至此，卡尔曼滤波器的基本推导已经完成。

4.简单讨论

这个只是一个非常简化的例子，有很多问题没有展开，例如何时卡尔曼滤波器给出的结果才是最优的和为什么是最优的。这里只讨论几个简单的问题。

卡尔曼增益的意义

在上面的例子中， σ21σ21+σ22 是卡尔曼增益，我们可以看到它其实是对预测和测量准确性的一个比重。如果我们对于预测的信心相对大，卡尔曼增益就会偏小(接近0)，反之，如果我们对于观测的信心相对大，卡尔曼增益就会相对偏大(接近1)。

观察式子(5)和(6)可以发现，当卡尔曼增益偏小时，观测步的结果偏向于接近预测步的结果(观测结果被更大程度地忽略)，而卡尔曼增益偏大时，观测步的结果则更多取信于观测到的距离。

简单说来，卡尔曼滤波器会选择性地考虑预测和观测的可信程度，并会体现在观测步的输出上。

协方差/方差

实际上，在很多情况下，我们并不能确定观测或者预测的协方差。例如在上面这个例子里面，如何知道蓝色分布(观测)的方差？也许可以通过信号的噪声和浮动的幅度来确定，但在很多场景里，这个不见得很容易，我们需要有一些合理的假设。

效果

整体说来，卡尔曼滤波器的效果是能够使观测的状态更加平滑，去除毛刺。

---

References 
1.Faragher, Ramsey. “Understanding the basis of the Kalman filter via a simple and intuitive derivation.” IEEE Signal processing magazine 29.5 (2012): 128-132.

---

1. 这个其实并不必要，但为了简化模型可以先这样假设。 ↩