看完了sparse coding,开始看ICA模型,本来ng的教程上面就只有一个简短的介绍,怎奈自己有强迫症,爱钻牛角尖,于是乎就搜索了一些ICA的介绍文章(都是从百度文库中搜来的),看完之后感觉这个略懂一二,遂写文以记之,一为加深印象,二为分享交流。
一:引言
ICA IndependentComponent Analysis 又名独立分量分析。
ICA是20世纪90年代发展起来的一种新的信号处理技术,它是从多维统计数据中找出隐含因子或分量的方法。从线性变换和线性空间角度,源信号为相互独立的非高斯信号,可以看作线性空间的基信号,而观测信号则为源信号的线性组合,ICA就是在源信号和线性变换均不可知的情况下,从观测的混合信号中估计出数据空间的基本结构或者说源信号。
二:ICA模型介绍
2.1.Blind Signal Separation, BSS问题
BSS问题,即盲信号分离问题,是信号处理中一个传统而又极具挑战性的课题。BSS是指仅从观测的混合信号(通常是多个传感器的输出)中恢复独立的源信号,这里的“盲”是指:1.源信号是不可观测的;2.混合系统是事先未知的。在科学研究和工程应用中,很多观测信号都可以假设成是不可见的源信号的混合。所谓的“鸡尾酒会”问题就是一个典型的例子,简单说就是当很多人(作为不同的声音源)同时在一个房间里说话时,声音信号由一组麦克风记录下来,这样每个麦克风记录的信号是所有人声音的一个混合,也就是通常所说的观测信号。问题是:如何只从这组观测信号中提取每个说话者的声音信号,即源信号。如果混合系统是已知的,则以上问题就退化成简单的求混合矩阵的逆矩阵。但是在更多的情况下,人们无法获取有关混合系统的先验知识,这就要求人们从观测信号来推断这个混合矩阵,实现盲源分离。
经典的鸡尾酒宴会问题(cocktail party problem)。假设在party中有n个人,他们可以同时说话,我们也在房间中一些角落里共放置了n个声音接收器用来记录声音。宴会后,从n个麦克风中得到一组数据Xi(Xi1,Xi2,……Xin)i=1,2……m,i表示采样的时间顺序,也就是说共得到了m组采样,每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
问题总结:
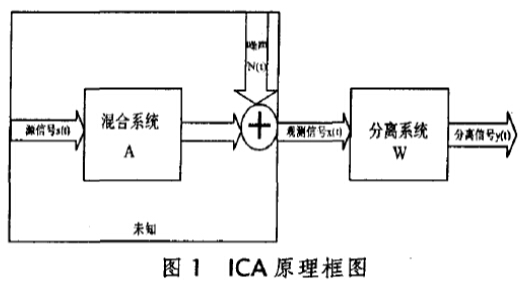
ICA的目的是对任何t,根据已知X(t)的在A未知的情况下求未知的S(t),ICA的思路是设置一个n*n维反混合阵W,经过变换后得到n维输出列向量Y(t)=[y1(t),y2(t),……y3(t)],即有 :





 本文介绍了ICA的基本概念,包括独立分量分析的目标是寻找观测信号的线性组合,以恢复出源信号。通过盲信号分离(BSS)问题阐述了ICA的应用背景,并以鸡尾酒宴会问题为例进行解释。文章还探讨了如何通过优化目标函数来度量分离信号的独立性,并介绍了概率论和信息论的基础知识,如熵、负熵和互信息在ICA中的作用。
本文介绍了ICA的基本概念,包括独立分量分析的目标是寻找观测信号的线性组合,以恢复出源信号。通过盲信号分离(BSS)问题阐述了ICA的应用背景,并以鸡尾酒宴会问题为例进行解释。文章还探讨了如何通过优化目标函数来度量分离信号的独立性,并介绍了概率论和信息论的基础知识,如熵、负熵和互信息在ICA中的作用。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 7365
7365

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








