人工智能/机器学习基础知识——聚类（原型聚类、密度聚类、层次聚类）

聚类

Clustering

原型聚类

Prototype-based Clustering

k均值

k-means

• Key Idea

  • 随机选择$k$个样本作为簇中心（簇均值向量），分别计算其余样本与$k$个簇中心的距离进而确定样本的簇标记，接着重新根据当前划分结果计算新的簇中心，迭代直至收敛

  • 聚簇中心不一定为数据样本点

• k-means目标：最小化平方误差

  $$E=\sum _{i=1}^k\sum _{\mathbf{x}\in C_i}{\Vert \mathbf{x}-{\mathbf{\mu }}_i\Vert }_2^2$$

  

学习向量量化

Learning Vector Quantization，LVQ

• LVQ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类

  

高斯混合聚类

Mixture-of-Gaussian

密度聚类

Density-based Clustering

Canopy

Canopy

• Overview

  • Canopy属于一种粗粒度（Coarse-grained）的聚类算法，它使用一种简单、快捷的距离计算方式将数据集分为若干可重叠的子集，这种算法不需要指定$k$值、但精度较低，可以结合K-means算法一起使用：先由Canopy算法进行粗聚类得到$k$个质心，再使用K-means算法进行聚类

  • 聚簇中心一定为数据样本点

• 算法

  • 将原始数据组织成列表$L=[x_1,x_2,x_3,...,x_n]$，设定超参数$T_1$和$T_2$且$T_1>T_2$

  • 从列表$L$中随机选取一个样本作为第一个Canopy的质心，并将其从列表$L$中删除

  • 从列表$L$中随机选取一个样本$Q$，计算其到所有质心的距离，考察其中的最小距离$D$（重复执行该步）

    • 若$T_2<D<=T_1$，则给$Q$一个弱标记，表示$Q$属于该Canopy，并将$Q$加入其中（不从$L$中删除$Q$）

    • 若$D<=T_2$，则给$Q$一个强标记，表示$Q$属于该Canopy，且和质心非常接近，所以将该Canopy的质心设为所有强标记样本的中心位置，并将$Q$从列表$L$中删除

    • 若$D>T_1$，则$Q$形成一个新的聚簇，并将$Q$从列表$L$中删除

  

DBSCAN

CSDN

Density-Based Spatial Clustering of Applications with Noise

• Overview

  • 相对于K-means类算法来说，DBSCAN无需预先指定簇个数

  • 最终聚类簇个数不确定

  • 聚簇中心一定为数据样本点

  

• 两个超参数

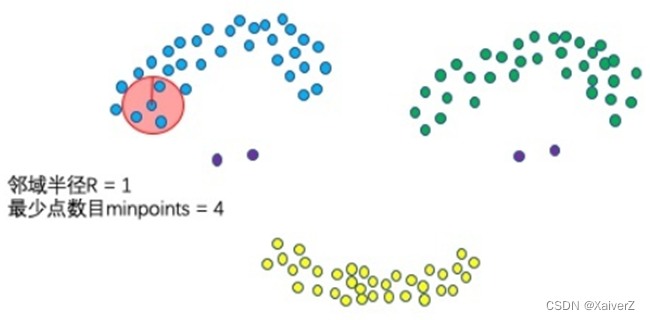
  • 邻域半径：Eps

  • 最少点数目：MinPts

  

• 三种点类别

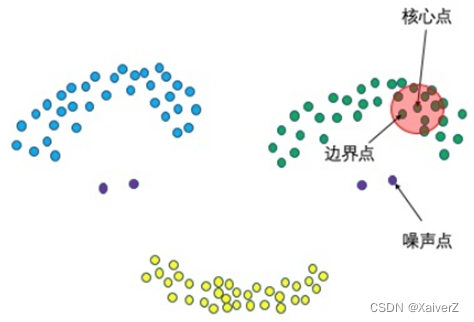
  • 核心点：邻域范围内点数量大于最少点数目（Minpoints）

  • 边界点：不属于核心点但在某个核心点的邻域内

  • 噪声点：其余点

  

• 四种点关系

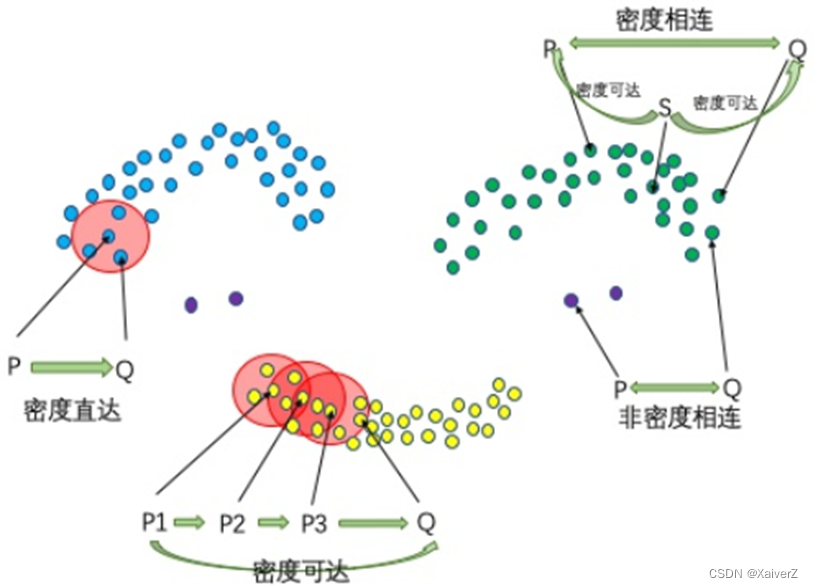
  • 密度直达：核心点到其邻域范围内的任意点是密度直达的

    • 不对称（$P$密度直达$Q$，但$Q$不一定密度直达$P$，因为密度直达要求密度直达发起者必须为核心点，到达点为其邻域内一点，而$Q$不一定为核心点）

  • 密度可达：由多个链式密度直达定义（$P_1$密度直达$P_2$，$P_2$密度直达$P_3$，$P_3$密度直达$Q$，则$P_1$密度可达$Q$）

    • 不对称

  • 密度相连：若存在一个核心点$S$，使$S$到$P$和$Q$都密度可达，则$P$与$Q$密度相连

    • 对称

  • 非密度相连：除了上述三种关系之外

  

• 算法

  • 从数据集中任意选取一个数据对象点$p$

  • 如果对于参数Eps和MinPts，所选取的数据对象点$p$为核心点，则找出所有从$p$密度可达的数据对象点，形成一个簇

  • 如果选取的数据对象点$p$不是核心点，则选取另一个数据对象，回到上一步

  • 重复前两步，直到所有点都被处理

  

• 伪码

  

• 优势

  • 无需指定聚类簇数

  • 对异常点不敏感（一些扰动包可丢弃）

• 缺陷

  • 对密度敏感。若数据密度分布不均匀效果差

OPTICS

CSDN

CSDN

CSDN

知乎

Ordering Point To Idenfy the Cluster Structure

• Key Insight

  • 针对DBSCAN无法适应数据密度不均匀的情况进行了改进，在DBSCAN的基本概念中又扩充了一些概念

• 两个距离

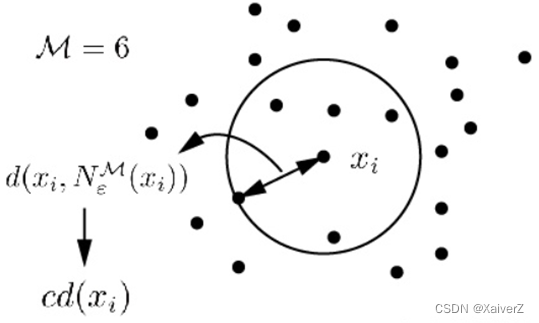
  • 核心距离：对于给定的最少点个数，使某个数据点$x_i\in X$成为核心点的最小邻域半径为$x_i$的核心距离

    $$cd\left(x_i\right)=\{\begin{array}{ll}\text{ UNDEFINED, }& \text{ if }\left|N_{\epsilon }\left(x_i\right)\right|<\mathcal{M}\\ d\left(x_i,N_{\epsilon }^{\mathcal{M}}\left(x_i\right)\right),& \text{ otherwise }\end{array}$$

    

  • 可达距离

    r d ( x j , x i ) = {  UNDEFINED,   if  ∣ N e ( x i ) ∣ < M max ⁡ { c d ( x i ) , d ( x i , x j ) } ,  otherwise  r d\left(x_{j}, x_{i}\right)= \begin{cases}\text { UNDEFINED, } & \text { if }\left|N_{e}\left(x_{i}\right)\right|<\mathcal{M} \\ \max \left\{c d\left(x_{i}\right), d\left(x_{i}, x_{j}\right)\right\}, & \text { otherwise }\end{cases} rd(xj​,xi​)={ UNDEFINED, max{cd(xi​),d(xi​,xj​)},​ if ∣Ne​(xi​)∣<M otherwise ​
    $N_e(x_i)$为$x_i$在邻域半径$e$范围内的点集合

    

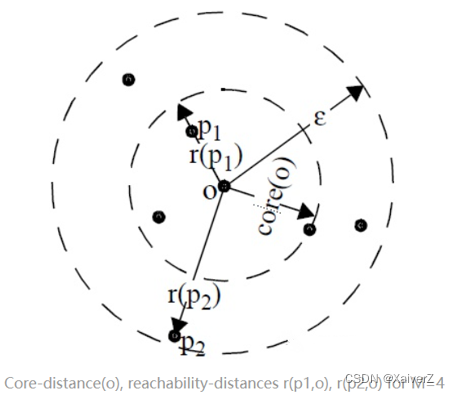
• 算法

  已知原始数据队列$D$，创建两个新队列：有序队列和结果队列。有序队列用来存储核心点的密度直达对象，并按其与核心点的可达距离升序排列；结果队列用来存储样本点的输出次序。可以把有序队列里面存放的数据点理解为待处理数据，而结果队列里放的是已经处理完的数据

  • 若样本集$D$中所有数据均处理完毕，则算法结束。选择一个未处理（即不在结果队列中）且为核心点的样本，找到其所有密度直达的点，如果这些密度直达的样本点不存在于结果队列中，则将其放入有序队列中，并按与核心点的可达距离排序

  • 若有序队列为空，则返回上一步重新选取数据点。否则，从有序队列中取出第一个样本点（即可达距离最小的样本点）进行进一步处理，并将取出的样本点保存至结果队列中（如果它不存在于结果队列当中的话），进行下述处理

    • 判断取出的点是否为核心点，若不是，返回上一步重新从有序队列中选取数据点；若为核心点，则继续找到该点的所有密度直达点，进行处理

      • 若密度直达点已存在于结果队列中，则不处理；否则下一步

      • 如果有序队列中已经存在该密度直达点，若此时新的可达距离小于旧的可达距离（注意此处的可达距离指的是某点相对于两个核心点的可达距离），则用新可达距离取代旧可达距离，并将有序队列重新排序（因为一个对象可能由多个核心点密度直达，因此，可达距离近的肯定是更好的选择）

      • 如果有序队列中不存在该密度直达点，则插入该点，并对有序队列重新排序

  • 迭代上述两步

  • 算法结束，输出结果队列中的有序样本点

• 核心思想

  若一个点可由多个核心点密度直达，那么这个点更应该属于可达距离更近的那个核心点

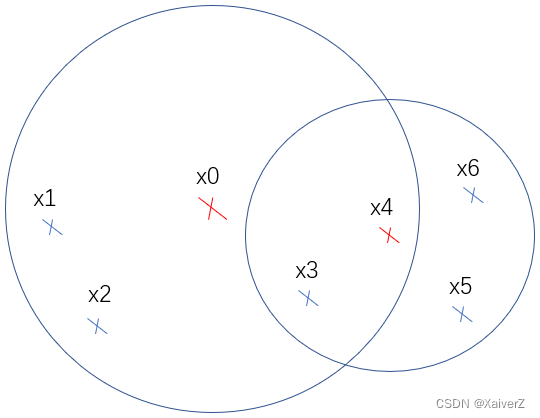
  • 假设算法开始，选中$x_0$核心点，找出其所有密度直达的点并加入有序队列排序$$[x_4,x_1,x_2,x_3]$$

  • 接下来取出有序列表第一个点$x_4$。由于$x_4$也为核心点，故找出其所有密度直达的点$x_3,x_5,x_6$，并对其进行处理

  • 选中$x_3$，不存在结果队列，但已存在于有序队列中。假设$rd(x_3,x_0)>rd(x_3,x_4)$，即新的可达距离小于旧的可达距离，故使用新距离替代旧距离，重新对有序列表排序$$[x_4,x_3,x_1,x_2]$$

  • 有序列表的这种变化说明了OPTICS的核心思想，若一个样本点可由多个核心点密度直达，那么这个点更应该属于可达距离更近的那个核心点。表现在有序列表上就是$x_3$更靠近$x_4$了，在输出时两者自然更靠近，属于同一簇的概率更大

  

• Example

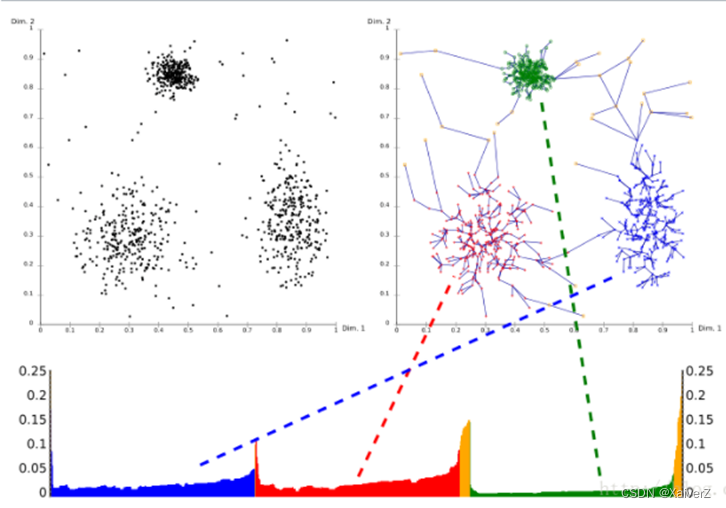
  横坐标为输出样本点的次序，纵坐标为可达距离

  • “凹陷”越深，说明该聚簇越紧密

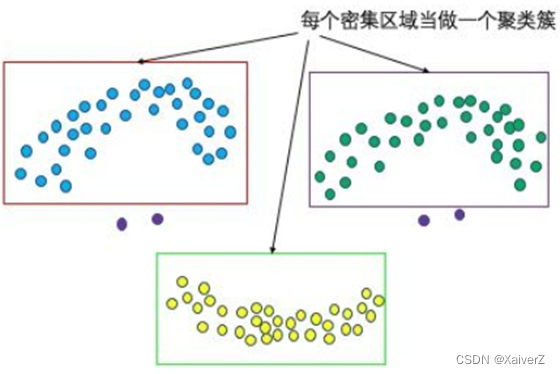
  • 从下图可以看出，三个聚簇的密度分布不均匀，上方聚簇的密度比下方两个聚簇的密度要大。若使用DBSCAN算法进行聚类，采用和上方聚簇密度相当的邻域半径与最小点数目设置，则在聚类是虽然对上方聚簇的效果较好，但对下方两个聚簇的效果就很差（甚至很难找到核心点，因为密度比上方聚簇小很多）

  

层次聚类

Hierarchical Clustering

• 自底向上 or 自顶向下

AGNES

自底向上层次聚类

• 先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直到达到预设的聚类簇个数

• 簇间度量

  • 最小距离

    $$d_{\min }\left(C_i,C_j\right)=\underset{\mathbf{x}\in C_i,\mathbf{z}\in C_j}{\min }\mathrm{dist}(\mathbf{x},\mathbf{z})$$
    单链接（Single-linkage）

  • 最大距离

    $$d_{\max }\left(C_i,C_j\right)=\underset{\mathbf{x}\in C_i,\mathbf{z}\in C_j}{\max }\mathrm{dist}(\mathbf{x},\mathbf{z})$$
    全链接（Complete-linkage）

  • 平均距离

    $$d_{\mathrm{avg}}\left(C_i,C_j\right)=\frac{1}{\left|C_i\right|\left|C_j\right|}\sum _{\mathbf{x}\in C_i}\sum _{z\in C_j}\mathrm{dist}(\mathbf{x},\mathbf{z})$$
    均链接（Average-linkage）