CS224W: Machine Learning with Graphs
Stanford / Winter 2021
13-communities
-
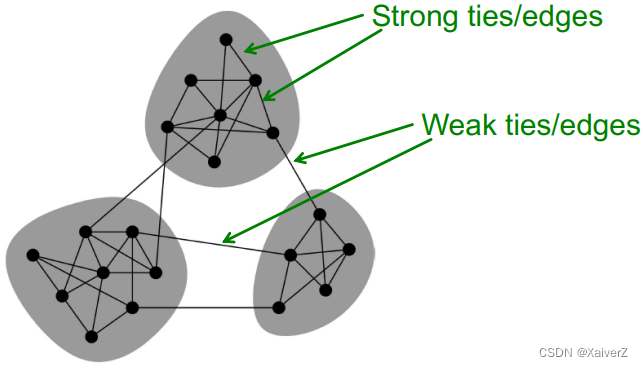
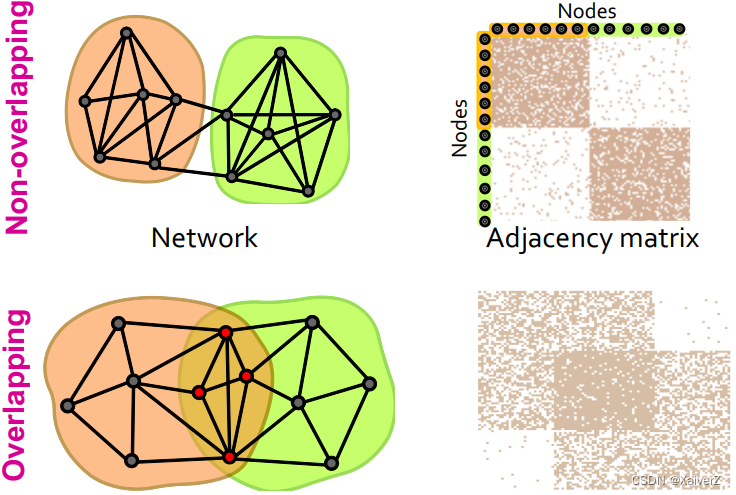
Network communities
- Sets of nodes with lots of internal connections and few external ones (to the rest of the network) (内部连边多,与网络其余部分连边少)
-
Null Model: Configuration Model
Given real G G G on n n n nodes and m m m edges, construct rewired network G ′ G' G′. Consider G ′ G' G′ as a multigraph (multiple edges exist between nodes)
-
Same degree distribution but uniformly random connections (节点度分布相同,连边随机)
-
The expected number of edges between nodes i i i and j j j of degrees k i k_i ki and k j k_j kj equals (两节点间期望连边数量)
k i ⋅ k j 2 m = k i k j 2 m k_{i} \cdot \frac{k_{j}}{2 m}=\frac{k_{i} k_{j}}{2 m} ki⋅2mkj=2mkikj
-
There are 2 m 2m 2m directed edges (counting i → j i \rightarrow j i→j and j → i j \rightarrow i j→i) in total
-
For each of k i k_i ki out-going edges from node i i i, the chance of it landing to node j j j is k j / 2 m k_j/2m kj/2m, hence k i k j / 2 m k_ik_j/2m kikj/2m
-
-
The expected number of edges in (multigraph) G ′ G' G′ (随机图 G ′ G' G′的总期望边数)
1 2 ∑ i ∈ N ∑ j ∈ N k i k j 2 m = 1 2 ⋅ 1 2 m ∑ i ∈ N k i ( ∑ j ∈ N k j ) = 1 4 m 2 m ⋅ 2 m = m \begin{aligned} &\frac{1}{2} \sum_{i \in N} \sum_{j \in N} \frac{k_{i} k_{j}}{2 m}=\frac{1}{2} \cdot \frac{1}{2 m} \sum_{i \in N} k_{i}\left(\sum_{j \in N} k_{j}\right)= \\ &\frac{1}{4 m} 2 m \cdot 2 m=m \end{aligned} 21i∈N∑j∈N∑2mkikj=21⋅2m1i∈N∑ki j∈N∑kj =4m12m⋅2m=m
-
所以,使用null model,图的节点分布与边总数都被保留
-
-
Modularity Q Q Q
-
A measure of how well a network is partitioned into communities
-
Given a partitioning of the network into groups disjoint s ∈ S s \in S s∈S
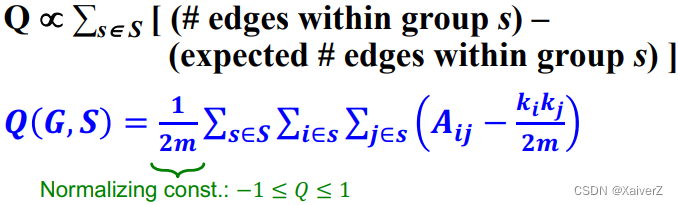
-
Modularity values take range [ − 1 , 1 ] [-1,1] [−1,1]
-
It is positive if the number of edges within groups exceeds the expected number
-
Q Q Q greater than 0.3-0.7 means significant community structure
-
-
Louvain Algorithm
Louvain Algorithm
-
Overview
-
For community detection
- O ( n l o g n ) O(nlogn) O(nlogn) run time
-
Supports weighted graphs
-
Can detect hierarchical communities
-
-
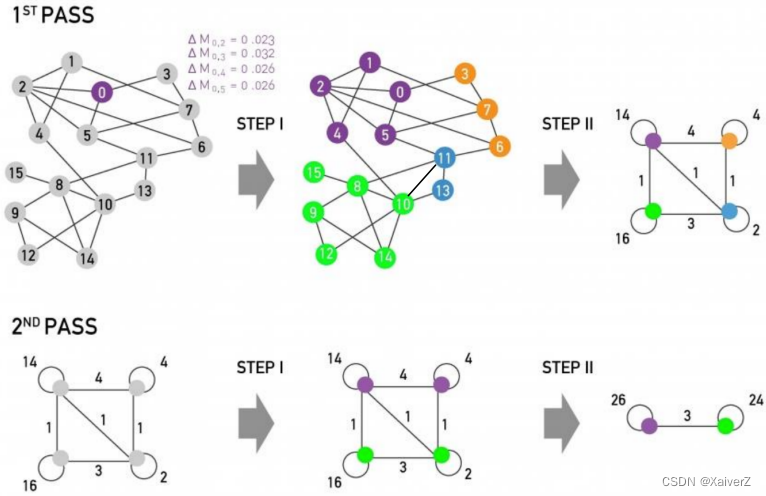
Louvain: 1 s t 1^{st} 1st phase (Partitioning)
-
Put each node in a graph into a distinct community (one node per community) (将每个点都划分进一个单独的社区)
-
For each node i i i, the algorithm performs two calculations (处理节点的顺序影响最后的结果,但研究表明这种影响程度不大,可以忽略)
-
Compute the modularity delta ( Δ Q \Delta Q ΔQ) when putting node i i i into the community of some neighbor j j j (计算把节点 i i i放入其他社区的 Δ Q \Delta Q ΔQ)
-
Move i i i to a community of node j j j that yields the largest gain in Δ Q \Delta Q ΔQ (将节点 i i i移入产生最大 Δ Q \Delta Q ΔQ的社区)
-
-
Phase 1 runs until no movement yields a gain (直到移动节点不产生任何的 Δ Q \Delta Q ΔQ变化)

-
-
Louvain: 2 n d 2^{nd} 2nd phase (Restructuring)
-
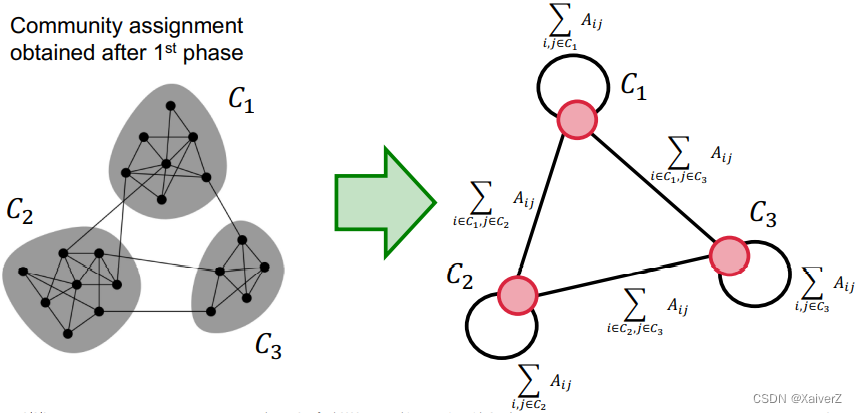
The communities obtained in the first phase are contracted into super-nodes, and the network is created accordingly (第一阶段检测出的每个社区都被转换成超级节点)
-
Super-nodes are connected if there is at least one edge between the nodes of the corresponding communities (如果超级节点所属的社区之间至少有一条连边,那么对应的超级节点之间也有连边)
-
The weight of the edge between the two super-nodes is the sum of the weights from all edges between their corresponding communities (超级节点之间连边的权重为对应的社区之间的所有连边权重之和)
-
-
Phase 1 is then run on the super-node network (第一阶段继续在超级节点上进行,因此自底层向高层产生层次聚类的结果)
-
Modularity Gain
Modularity Gain
-
将节点 i i i从社区 D D D移动到社区 C C C所产生的 Δ Q \Delta Q ΔQ是多少?
Δ Q ( D → i → C ) = Δ Q ( D → i ) + Δ Q ( i → C ) \Delta Q(D \rightarrow i \rightarrow C)=\Delta Q(D \rightarrow i)+\Delta Q(i \rightarrow C) ΔQ(D→i→C)=ΔQ(D→i)+ΔQ(i→C)
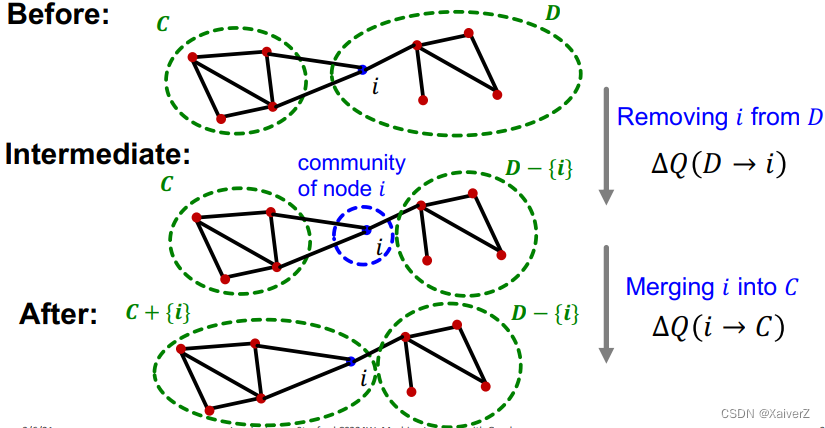
-
Deriving Δ Q ( i → C ) \Delta Q(i \rightarrow C) ΔQ(i→C)
-
First, we derive modularity within C C C, i.e., Q ( C ) Q(C) Q(C)
-
Σ i n ≡ ∑ i , j ∈ C A i j \boldsymbol{\Sigma}_{\boldsymbol{i n}} \equiv \sum_{i, j \in C} A_{i j} Σin≡∑i,j∈CAij: sum of link weights between nodes in C C C
-
Σ tot ≡ ∑ i ∈ C k i \boldsymbol{\Sigma}_{\text {tot }} \equiv \sum_{i \in C} k_{i} Σtot ≡∑i∈Cki: sum of all link weights of nodes in C C C
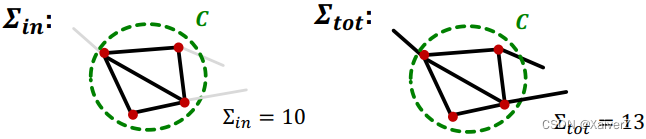
Q ( C ) ≡ 1 2 m ∑ i , j ∈ C [ A i j − k i k j 2 m ] = ∑ i , j ∈ C A i j 2 m − ( ∑ i ∈ C k i ) ( ∑ j ∈ C k j ) ( 2 m ) 2 = Σ i n 2 m − ( Σ t o t 2 m ) 2 Q(C) \equiv \frac{1}{2 m} \sum_{i, j \in C}\left[A_{i j}-\frac{k_{i} k_{j}}{2 m}\right]=\frac{\sum_{i, j \in C} A_{i j}}{2 m}-\frac{\left(\sum_{i \in C} k_{i}\right)\left(\sum_{j \in C} k_{j}\right)}{(2 m)^{2}} = \frac{\Sigma_{i n}}{2 m}-\left(\frac{\Sigma_{t o t}}{2 m}\right)^{2} Q(C)≡2m1i,j∈C∑[Aij−2mkikj]=2m∑i,j∈CAij−(2m)2(∑i∈Cki)(∑j∈Ckj)=2mΣin−(2mΣtot)2
-
-
Second, further define something useful
-
k i , i n ≡ ∑ j ∈ C A i j + ∑ j ∈ C A j i \boldsymbol{k}_{i, i n} \equiv \sum_{j \in C} A_{i j}+\sum_{j \in C} A_{j i} ki,in≡∑j∈CAij+∑j∈CAji: sum of link weights between node i i i and C C C
-
k i \boldsymbol{k}_{\boldsymbol{i}} ki: sum of all link weights (i.e., degree) of node i i i

-
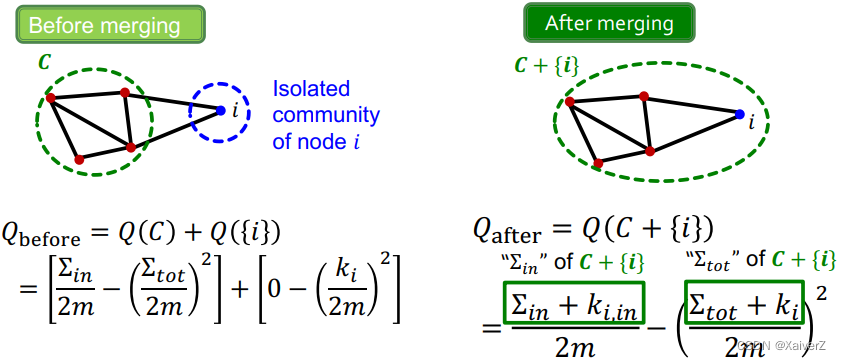
Q before = Q ( C ) + Q ( { i } ) = [ Σ in 2 m − ( Σ tot 2 m ) 2 ] + [ 0 − ( k i 2 m ) 2 ] \begin{aligned} &Q_{\text {before }}=Q(C)+Q(\{i\}) \\ &\quad=\left[\frac{\Sigma_{\text {in }}}{2 m}-\left(\frac{\Sigma_{\text {tot }}}{2 m}\right)^{2}\right]+\left[0-\left(\frac{k_{i}}{2 m}\right)^{2}\right] \end{aligned} Qbefore =Q(C)+Q({i})=[2mΣin −(2mΣtot )2]+[0−(2mki)2]
Q a f t e r = Q ( C + { i } ) = ∑ i n + k i , i n 2 m − ( ∑ t o t + k i 2 m ) 2 \begin{aligned} &Q_{\mathrm{after}}=Q(C+\{i\}) \\ &\quad=\frac{\sum_{i n}+k_{i, i n}}{2 m}-\left(\frac{\sum_{t o t}+k_{i}}{2 m}\right)^{2} \end{aligned} Qafter=Q(C+{i})=2m∑in+ki,in−(2m∑tot+ki)2
Δ Q ( i → C ) = Q a f t e r − Q b e f o r e = [ Σ i n + k i , i n 2 m − ( Σ t o t + k i 2 m ) 2 ] − [ Σ i n 2 m − ( Σ t o t 2 m ) 2 − ( k i 2 m ) 2 ] \begin{aligned} \Delta Q(i \rightarrow C)=& Q_{\mathrm{after}}-Q_{\mathrm{before}} \\ =& {\left[\frac{\Sigma_{i n}+k_{i, i n}}{2 m}-\left(\frac{\Sigma_{t o t}+k_{i}}{2 m}\right)^{2}\right] } \\ &-\left[\frac{\Sigma_{i n}}{2 m}-\left(\frac{\Sigma_{t o t}}{2 m}\right)^{2}-\left(\frac{k_{i}}{2 m}\right)^{2}\right] \end{aligned} ΔQ(i→C)==Qafter−Qbefore[2mΣin+ki,in−(2mΣtot+ki)2]−[2mΣin−(2mΣtot)2−(2mki)2]
- Δ Q ( D → i ) \Delta Q(D \rightarrow i) ΔQ(D→i) can be derived similarly
Δ Q ( D → i → C ) = Δ Q ( D → i ) + Δ Q ( i → C ) \Delta Q(D \rightarrow i \rightarrow C)=\Delta Q(D \rightarrow i)+\Delta Q(i \rightarrow C) ΔQ(D→i→C)=ΔQ(D→i)+ΔQ(i→C)
-
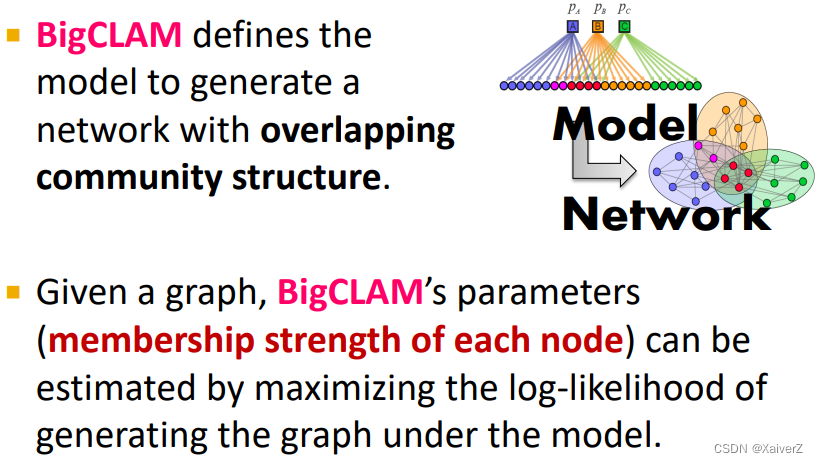
Detecting Overlapping Communities: BigCLAM
Detecting Overlapping Communities: BigCLAM
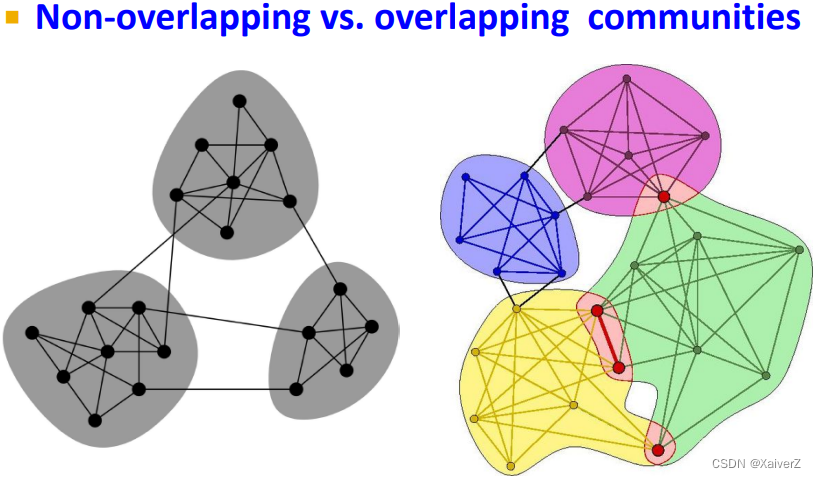
Community Affiliation Graph Model (AGM)
Community Affiliation Graph Model (AGM)
-
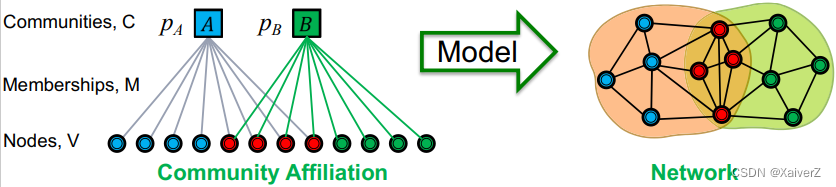
Key Insight: How is a network generated from community affiliations? (如何从社区的从属关系中生成出一个网络?)
Given parameters ( V , C , M , { p c } ) (V,C,M,\{p_c\}) (V,C,M,{pc})
-
Node in community c c c connect to each other by flipping a coin with probability p c p_c pc (同属同一个社区的两个节点之间有连边的概率为二项分布)
-
Nodes that belong to multiple communities have multiple coin flips (从属多个社区的节点有多次连边的机会,因为在每个社区内都会有一次机会)
p ( u , v ) = 1 − ∏ c ∈ M u ∩ M v ( 1 − p c ) p(u, v)=1-\prod_{c \in M_{u} \cap M_{v}}\left(1-p_{c}\right) p(u,v)=1−c∈Mu∩Mv∏(1−pc)
-
-
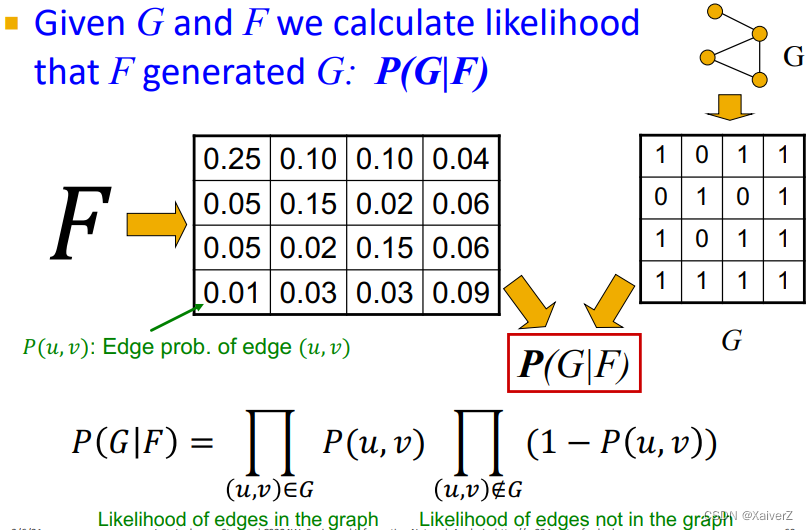
Key Insight: Detecting communities with AGM given a graph, find the model F F F (如何从生成的网络中倒推AGM模型的参数(BigCLAM Model))
Maximum likelihood estimation
-
Given real graph G G G
-
Find model/parameters F F F which

-
最大化Graph Likelihood P ( G ∣ F ) P(G|F) P(G∣F):最大化在图中连边的似然概率,最小化在图中没连边的似然概率
-
-
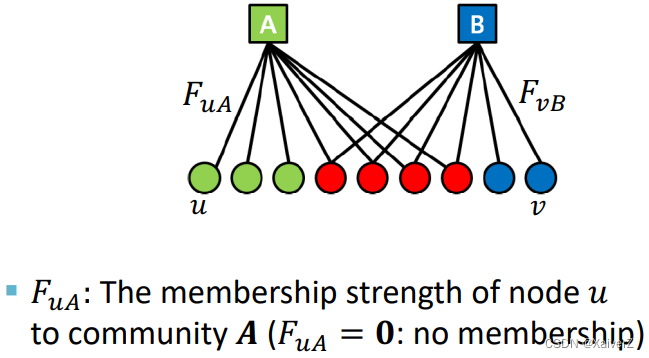
“Relax” the AGM: Memberships have strengths
-
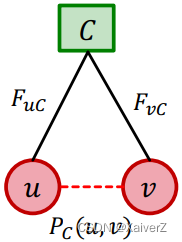
For community C C C, we model the probability of u u u and v v v being connected as
P C ( u , v ) = 1 − exp ( − F u C ⋅ F v C ) P_{C}(u, v)=1-\exp \left(-F_{u C} \cdot F_{v C}\right) PC(u,v)=1−exp(−FuC⋅FvC)
其中, F x x ≥ 0 F_{xx} \geq 0 Fxx≥0, 0 ≤ P C ( u , v ) ≤ 1 0 \leq P_{C}(u, v) \leq 1 0≤PC(u,v)≤1-
两个节点不相连,当且仅当双方至少有一个节点的 F C = 0 F_C = 0 FC=0
-
两个节点相连,当且仅当双方的 F C F_C FC都很大
-
-
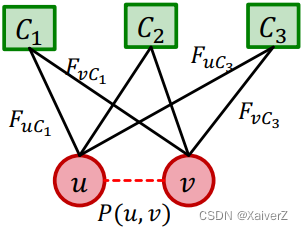
对于从属多个社区的节点 u u u和 v v v来说,两者相连的概率为
P ( u , v ) = 1 − ∏ C ∈ Γ ( 1 − P C ( u , v ) ) P(u, v)=1-\prod_{C \in \Gamma}\left(1-P_{C}(u, v)\right) P(u,v)=1−C∈Γ∏(1−PC(u,v))
-
-
BigCLAM Model

P ( u , v ) = 1 − exp ( − F u T F v ) \mathrm{P}(u, v)=1-\exp \left(-F_{u}^{T} F_{v}\right) P(u,v)=1−exp(−FuTFv)
-
Given a network G ( V , E ) G(V,E) G(V,E), we maximize the likelihood (probability) of G G G under our model
P ( G ∣ F ) = ∏ ( u , v ) ∈ E P ( u , v ) ∏ ( u , v ) ∉ E ( 1 − P ( u , v ) ) = ∏ ( u , v ) ∈ E ( 1 − exp ( − F u T F v ) ) ∏ ( u , v ) ∉ E exp ( − F u T F v ) \begin{aligned} P(G \mid \boldsymbol{F}) &=\prod_{(u, v) \in E} P(u, v) \prod_{(u, v) \notin E}(1-P(u, v)) \\ &=\prod_{(u, v) \in E}\left(\mathbf{1}-\exp \left(-\boldsymbol{F}_{u}^{\boldsymbol{T}} \boldsymbol{F}_{v}\right)\right) \prod_{(u, v) \notin E} \exp \left(-\boldsymbol{F}_{u}^{\boldsymbol{T}} \boldsymbol{F}_{v}\right) \end{aligned} P(G∣F)=(u,v)∈E∏P(u,v)(u,v)∈/E∏(1−P(u,v))=(u,v)∈E∏(1−exp(−FuTFv))(u,v)∈/E∏exp(−FuTFv)
-
Likelihood involves a product of many small probabilities -> Numerically unstable (似然概率包含很多小概率值的相乘->数值不稳定)
-
We consider the log likelihood (所以考虑最大化对数似然函数)
log ( P ( G ∣ F ) ) = log ( ∏ ( u , v ) ∈ E ( 1 − exp ( − F u T F v ) ) ∏ ( u , v ) ∉ E exp ( − F u T F v ) ) = ∑ ( u , v ) ∈ E log ( 1 − exp ( − F u T F v ) ) − ∑ ( u , v ) ∉ E F u T F v ≡ ℓ ( F ) \begin{aligned} &\log (P(G \mid \boldsymbol{F})) \\ &=\log \left(\prod_{(u, v) \in E}\left(1-\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right) \prod_{(u, v) \notin E} \exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right) \\ &=\sum_{(u, v) \in E} \log \left(1-\exp \left(-\boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v}\right)\right)-\sum_{(u, v) \notin E} \boldsymbol{F}_{u}^{T} \boldsymbol{F}_{v} \\ &\equiv \ell(\boldsymbol{F}) \end{aligned} log(P(G∣F))=log (u,v)∈E∏(1−exp(−FuTFv))(u,v)∈/E∏exp(−FuTFv) =(u,v)∈E∑log(1−exp(−FuTFv))−(u,v)∈/E∑FuTFv≡ℓ(F)
-
Optimizing ℓ ( F ) \ell(\boldsymbol{F}) ℓ(F)
-
Start with random membership F F F and Iterate until convergence
-
For u ∈ V u \in V u∈V
-
Update membership F u F_u Fu for node u u u while fixing the memberships of all other nodes
-
Specifically, we do gradient ascent, where we make small changes to F u F_u Fu that lead to increase in log-likelihood
∇ ℓ ( F ) = ∑ v ∈ N ( u ) ( exp ( − F u T F v ) 1 − exp ( − F u T F v ) ) ⋅ F v − ∑ v ∉ N ( u ) F v \nabla \ell(F)=\sum_{v \in \mathcal{N}(u)}\left(\frac{\exp \left(-F_{u}^{T} F_{v}\right)}{1-\exp \left(-F_{u}^{T} F_{v}\right)}\right) \cdot F_{v}-\sum_{v \notin \mathcal{N}(u)} F_{v} ∇ℓ(F)=v∈N(u)∑(1−exp(−FuTFv)exp(−FuTFv))⋅Fv−v∈/N(u)∑Fv
-
-
-
-
Time complexity of BigCLAM gradient ascent






















 601
601











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








