模式识别/机器学习百题（含大部分答案）

最新推荐文章于 2025-04-10 16:10:39 发布

withchris

最新推荐文章于 2025-04-10 16:10:39 发布

阅读量10w+

点赞数 45

分类专栏：机器学习文章标签：矩阵论

本文链接：https://blog.csdn.net/withchris/article/details/62419295

版权

一、概论

1、简述模式的概念和它的直观特性，解释什么是模式识别，同时绘出模式识别系统的组成框图，并说明各部分的主要功能特性。

对于存在于时间和空间中，可观察的物体，如果我们可以区分它们是否相同或相似，都可以称之为“模式”（或“模式类”）。

模式所指的不是事物本身，而是从事物中获得的信息。因此，模式常常表现为具有时间和空间分布的信息。

模式的直观特性包括：可观察性，可区分性，相似性。

模式识别就是对模式的区分和认识，把对象根据其特征归到若干类别中的适当一类。

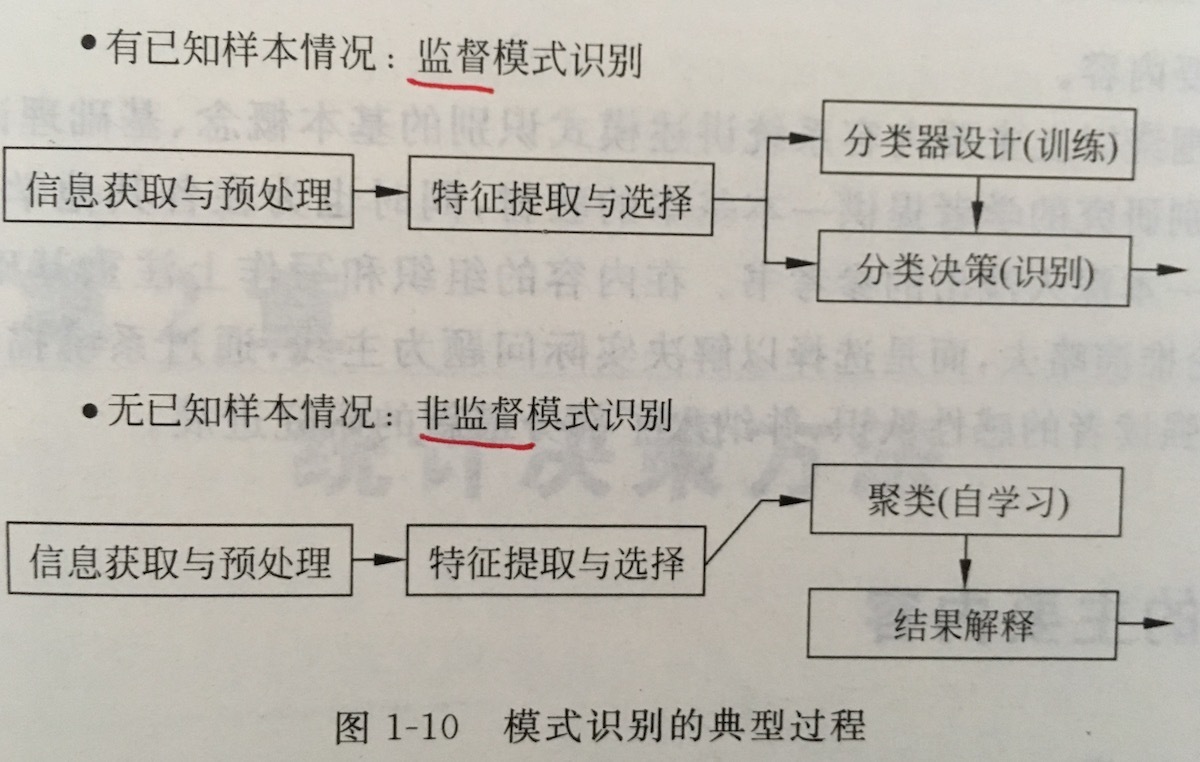
模式识别系统的组成框图如下图所示。一个模式识别系统通常包括：原始数据获取与预处理、特征提取与选择、分类或聚类、后处理四个步骤。

这里写图片描述

监督模式识别过程可归纳为五个基本步骤：分析问题、原始特征获取、特征提取与选择、分类器设计、分类决策。

非监督模式识别过程可归纳为五个基本步骤：分析问题、原始特征获取、特征提取与选择、聚类分析、结果解释。

每部分说明略。

2、简述模式识别系统中模式处理的完整过程，和一个分类器的设计过程。

模式处理的完整过程可归纳为：数据/信息获取与预处理、特征提取与选择、分类或聚类、后处理四个步骤。

在统计决策中，分类器设计的过程包括：样本（类条件）概率密度形式假定、参数或非参数密度估计、确定准则函数、确定决策规则。

在基于样本直接设计的分类器中，分类器设计过程包括：确定判别函数类型（线性、二次、决策树、神经网络等）、确定学习目标（准则函数）、确定优化算法，在训练数据上学习分类器、在测试数据上评价分类器、解释分析。

3、给出机器学习问题的形式化表示，并解释学习机器的推广能力。

（1）机器学习的形式化表示

已知变量 $y$ 与输入 $x$ 之间存在一定的未知依赖关系，即存在一个未知的映射 $F(x,y)$ 。

机器学习就是根据 $n$ 个独立同分布的观测样本 $\\{(x_1,y_1), \cdots, (x_n,y_n)\\}$ ，在一组函数 $\\{f(x,\omega)\\}$ 中求一个最优的函数，使预测的期望风险 $R(\omega) = L(y,f(x,\omega)) \text{d} F(x,y)$ 最小。

其中 $F(x,y)$ 表示所有可能出现的输入 $x$ 与输出 $y$ 的联合概率模型。

$\\{f(x,\omega)\\}$ 被称为预测函数集， $\omega \in \Omega$ 为函数的广义参数，故 $\\{f(x,\omega)\\}$ 可以表示任意函数集。

$L(y,f(x,\omega))$ 是使用 $f(x,\omega)$ 对 $y$ 进行预测而造成的损失。

简而言之，机器学习，就是在一组设定的函数集中寻找使期望风险最小的最优函数。

（2）学习机器的推广能力

模式识别是一种基于数据的机器学习，学习的目的不仅是要对训练样本正确分类，而是要能够对所有可能样本都正确分类，这种能力叫做推广能力。

4、区别于基于模型的模式识别方法（统计决策原理），基于数据的模式识别方法直接从样本设计分类器。从样本直接设计分类器，需要确定哪些基本要素？

需要确定三个基本要素：① 判别函数类型（函数集），② 学习目标（准则函数），③ 优化算法。

5、给定一组有类别标号（ $M$ 类）的样本 $x_1,\cdots,x_N\ (x_i \in R^d)$ 。现有两种特征提取方法 $F_1$ 和 $F_2$ ，和两种分类方法 $C_1$ 和 $C_2$ 。请设计一个实验方案，分别比较特征提取方法和分类方法的性能。写出详细实验过程。

采用 5-fold 交叉验证来评估

二、统计决策方法

1、简述多分类问题的最小错误率贝叶斯决策过程，并给出相应的最小分类错误率。

2、阐述最小风险贝叶斯决策原理和决策步骤，说明在什么情况下最小风险决策等价于最小错误率决策，并证明之。

（1）决策原理

最小风险贝叶斯决策的目标是，针对决策规则 $\alpha(x)$ ，最小化期望风险：

$\min_{\alpha} R(\alpha) = \int R(\alpha|x) p(x) \text{d}x$ .

由于 $R(\alpha|x)$ 和 $p(x)$ 非负，且 $p(x)$ 已知，与 $\alpha$ 无关，因而最小风险贝叶斯决策就是：

若 $R(\alpha_i|x) = \min_{j=1,\cdots,k} R(\alpha_j|x)$ ，则 $\alpha = \alpha_i$ .

其中 $R(\alpha_i|x) = E[\lambda_{ij}|x] = \sum_{j=1}^c P(\omega_j|x),\ i=1,\cdots,k$ ， $\lambda_{ij} = \lambda(\alpha_i, \omega_j)$ 表示实际为 $\omega_j$ 的向量决策为 $\alpha_i$ 的损失，可从事先定义的决策表查得.

（2）决策步骤

① 计算后验概率： $P(\omega_j|x) = \frac{p(x|\omega_j)P(\omega_j)}{\sum_{i=1}^c p(x|\omega_i)P(\omega_i)}$ .

② 利用决策表，计算条件风险： $R(\alpha_i|x) = \sum_{j=1}^c \lambda_{ij} P(\omega_j|x)$ .

③ 决策： $\alpha = \arg \min_i R(\alpha_i |x)$ .

（3）等价关系

当 $\lambda_{ii} = 0$ 且 $\lambda_{ij} = C\ (i\neq j)$ ，其中 $C$ 为某一常数时，最小风险贝叶斯决策等价于最小错误率贝叶斯决策。

证明：

满足上述条件时，条件风险 $R(\alpha_i|x) = \sum_{j=1, j\neq i}^c C P(\omega_j|x)$ .

则决策规则 $\alpha = \arg \min_i R(\alpha_i |x)$ 等价于：

$\alpha = \arg \min_i \sum_{j\neq i} C P(\omega_j|x) = \arg \min_i C P(e|x) = \arg\max_i P(\omega_i| x)$ .

因此，最小风险贝叶斯决策等价于最小错误率贝叶斯决策。

3、简述 Neyman-Pearson 决策原理。

Neyman-Pearson 决策原理是希望在固定一类错误率时，使另一类错误率尽可能小。

记 $P_1(e) = \int_{R_2} p(x|\omega_1) \text{d}x$ 和 $P_2(e) = \int_{R_1} p(x|\omega_2) \text{d}x$ 分别表示第一类错误率（假阴性率）和第二类错误率（假阳性率），则上述要求可表述为：

$\min P_1(e)$
$\text{s.t.} P_2(e) - \epsilon_0 = 0$ .

用拉格朗日乘子法，得：

$\gamma = \sum_{R_2} p(x|\omega_1)\text{d}x + \lambda[\int_{R_1} p(x|\omega_2)\text{d}x - \epsilon_0] = (1 - \lambda\epsilon_0) + \int_{R_1} [\lambda p(x|\omega_2) - p(x|\omega_1)]\text{d}x$ .

分别对 $\lambda$ 和决策边界 $t$ 求导，可得：

① $\lambda = \frac{p(x|\omega_1)}{p(x|\omega_2)}$ ，② $\int_{R_1} p(x|\omega_2) \text{d}x$ .

要使 $\gamma$ 最小，应选择 $R_1$ 使积分项内全为负值（否则可划出非负区域使之更小）。因此决策规则是：

若 $l(x) = \frac{p(x|\omega_1)}{p(x|\omega_2)} ### \lambda$ ，则 $x\in \omega_1$ ，否则 $x\in \omega_2$ .

（通常 $\lambda$ 很难求得封闭解，需要用数值方法求解）

4、给出假阳性率、假阴性率、灵敏度 $S_n$ （sensitivity）、特异度 $S_p$ （specificity）、第一类错误率 $\alpha$ 、第二类错误率 $\beta$ 、漏报、误报的关系，并给出相应的公式。

假阳性率就是假阳性样本占总阴性样本的比例。

假阴性率就是假阴性样本占总阳性样本的比例。

有：

$\alpha$ = 假阳性率 = 第一类错误率 = 误报率 = $\frac{\text{FP}}{\text{FP} + \text{TN}}$ = $P_1(e)$ = $\int_{R_2} p(x|\omega_1) \text{d}x$ .

$\beta$ = 假阴性率 = 第二类错误率 = 漏报率 = $\frac{\text{FN}}{\text{FN} + \text{TP}}$ = $P_2(e)$ = $\int_{R_1} p(x|\omega_2) \text{d}x$ .

其中 $\omega_1, \omega_2$ 分别表示阴性和阳性两个类别。

5、ROC 的全称是什么？ROC 曲线的横轴和纵轴各是什么？如何根据 ROC 曲线衡量一个方法的性能？给出 ROC 曲线的绘制步骤。

ROC 全称是 Receiver Operating Characteristic。

ROC 曲线的横轴是假阳性率，纵轴是假阴性率。

可以根据 ROC 曲线的曲线下面积 AUC (Area Under Curve) 来衡量一个方法的性能。

对于统计决策方法，每确定一个似然比阈值就决定了决策的真、假阳性率。因此ROC 曲线绘制步骤为：

① 在 $[0,1]$ 上均匀采样 $N$ 个点；
② 以每个点的值作为似然比阈值，根据公式 $P_1(e) = \int_{R_2} p(x|\omega_1) \text{d}x$ 和 $P_2(e) = \int_{R_1} p(x|\omega_2) \text{d}x$ 计算两类错误率，对应 ROC 上某个点；
③ 把这些点连接起来得到 ROC 曲线。

对于基于样本直接设计分类器的方法，ROC 曲线绘制步骤类似。只需将似然比阈值改成归一化后的分类器得分阈值，把两类错误率的计算公式改成 $\frac{\text{FP}}{\text{FP} + \text{TN}}$ 和 $\frac{\text{FN}}{\text{FN} + \text{TP}}$ 即可。

6、设 $p(x|\omega_i) \sim N(\mu_i, \Sigma_i),\ i=1,\cdots,c$ ，给出各类别的判别函数和决策面方程并计算错误率。同时说明在各类别协方差矩阵相等和不等的情况下，决策面各是什么形态。

7、疾病检查， $\omega_1$ 代表正常人， $\omega_2$ 代表患病者。假设先验概率 $P(\omega_1) = 0.9$ , $P(\omega_2) = 0.1$ 。现有一被检查者，观察值为 $x$ ，查得 $p(x|\omega_1) = 0.2$ , $p(x|\omega_2) = 0.4$ ，同时已知风险损失函数为 $\begin{bmatrix} \lambda_{11} & \lambda_{12} \\\\ \lambda_{21} & \lambda_{22} \end{bmatrix} = \begin{bmatrix} 0 & 6 \\\\ 1 & 0 \end{bmatrix}$ . 分别基于最小错误率和最小贝叶斯进行决策，并给出计算过程。

8、设 $d$ 维随机变量 $x$ 各分量间相互独立，且 $d$ 足够大，试基于中心极限定理估计贝叶斯错误率。

9、什么是统计决策？比较基于模型的方法和基于数据的方法。

统计决策的基本原理就是根据各类特征的概率模型来估算后验概率，通过比较后验概率进行决策。而通过贝叶斯公式，后验概率的比较可以转化为类条件概率密度的比较。

基于模型的方法是从模型的角度出发，把模式识别问题转化成了概率模型估计的问题。如果能够很好地建立和估计问题的概率模型，那么相应的分类决策问题就能被很好地解决。

基于数据的方法不依赖样本概率分布的假设，而直接从训练样本出发训练分类器。

三、概率密度函数的估计

1、比较四种方法：参数统计方法、非参数统计方法、前馈神经网络、支持向量机各有什么优缺点？

（1）参数统计方法

（2）非参数统计方法

优点：假设条件少，运算简单，方法直观容易理解，能够适应名义尺度和顺序尺度等对象。

缺点：方法简单，检验功效差，计算和存储要求高。

（3）前馈神经网络

优点：分类的准确度高,并行分布处理能力强,分布存储及学习能力强，对噪声神经有较强的鲁棒性和容错能力，能充分逼近复杂的非线性关系，具备联想记忆的功能等。特别重要的是，神经网络可以用来提取特征，这是许多其他机器学习方法所不具备的能力（例如使用autoencoder，不标注语料的情况下，可以得到原始数据的降维表示）。

缺点：需要大量的参数，如网络拓扑结构、权值和阈值的初始值；不能观察之间的学习过程，输出结果难以解释，会影响到结果的可信度和可接受程度；学习时间过长,甚至可能达不到学习的目的。

（4）支持向量机

优点：能解决小样本问题，能处理非线性问题，无局部极小值问题，能很好地处理高维数据，泛化能力强。

缺点：对核函数的高维映射解释能力不强（尤其是径向基函数），对缺失数据敏感，难以处理大规模数据，难以解决多分类问题（常用一对多、一对一、SVM 决策树），对非线性问题没有通用解决方案（有时候很难找到一个合适的核函数）。

注：缺失数据？

这里说的缺失数据是指缺失某些特征数据，向量数据不完整。SVM没有处理缺失值的策略（决策树有）。而SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM的性能很重要。缺失特征数据将影响训练结果的好坏。