SciPy 1.12 中文文档（二十三）

原文：docs.scipy.org/doc/scipy-1.12.0/index.html

scipy.optimize.NonlinearConstraint

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.NonlinearConstraint.html#scipy.optimize.NonlinearConstraint

class scipy.optimize.NonlinearConstraint(fun, lb, ub, jac='2-point', hess=<scipy.optimize._hessian_update_strategy.BFGS object>, keep_feasible=False, finite_diff_rel_step=None, finite_diff_jac_sparsity=None)

变量的非线性约束。

约束具有一般的不等式形式：

lb <= fun(x) <= ub 

这里独立变量向量 x 作为形状为 (n,) 的 ndarray 传递，并且fun返回一个有 m 个分量的向量。

可以使用相等的边界来表示等式约束，或者使用无限边界来表示单边约束。

参数：

fun：可调用函数

定义约束的函数。签名是 fun(x) -> array_like, shape (m,)。

lb, ub：array_like

约束的下界和上界。每个数组必须具有形状 (m,) 或者是一个标量，后一种情况下约束对所有约束分量是相同的。使用 np.inf 与适当的符号指定单边约束。将 lb 和 ub 的分量设置为相等表示等式约束。注意，可以通过设置 lb 和 ub 的不同分量来混合不同类型的约束：区间、单边或等式。

jac：{可调用函数, ‘2-point’, ‘3-point’, ‘cs’}，可选

计算雅可比矩阵的方法（一个 m×n 矩阵，其中元素 (i, j) 是 f[i] 对 x[j] 的偏导数）。关键字 {‘2-point’, ‘3-point’, ‘cs’} 选择数值估计的有限差分方案。一个可调用对象必须具有以下签名：jac(x) -> {ndarray, sparse matrix}, shape (m, n)。默认为 ‘2-point’。

hess：{可调用函数, ‘2-point’, ‘3-point’, ‘cs’, HessianUpdateStrategy, None}，可选

计算 Hessian 矩阵的方法。关键字 {‘2-point’, ‘3-point’, ‘cs’} 选择数值估计的有限差分方案。或者，实现了 HessianUpdateStrategy 接口的对象可以用来近似 Hessian。当前可用的实现是：

• BFGS （默认选项）
• SR1

一个可调用对象必须返回 dot(fun, v) 的 Hessian 矩阵，并且必须具有以下签名：hess(x, v) -> {LinearOperator, sparse matrix, array_like}, shape (n, n)。这里 v 是形状为 (m,) 的 ndarray，包含拉格朗日乘数。

keep_feasible：bool 类型的数组，可选

决定在迭代过程中是否保持约束分量的可行性。一个单一的值设置该属性对所有分量生效。默认值为 False。对于等式约束没有影响。

finite_diff_rel_step：None 或者 array_like，可选

有限差分近似的相对步长。默认为 None，根据有限差分方案自动选择合理值。

finite_diff_jac_sparsity: {None, array_like, sparse matrix}, optional

定义了有限差分估计雅可比矩阵的稀疏结构，其形状必须为 (m, n)。如果雅可比矩阵每行只有少量非零元素，在提供稀疏结构的情况下将大大加快计算速度。零条目意味着雅可比矩阵中对应元素恒为零。如果提供，则强制使用 ‘lsmr’ 信赖区域求解器。如果为 None（默认值），则将使用稠密差分。

注意事项

可用于近似雅可比或海森矩阵的有限差分方案 {‘2-point’, ‘3-point’, ‘cs’}。然而，我们不允许同时用于两者的近似。因此，每当通过有限差分估计雅可比时，我们要求使用一种拟牛顿策略估计海森矩阵。

方案 ‘cs’ 可能是最准确的，但要求函数能正确处理复杂输入，并在复平面上解析延拓。方案 ‘3-point’ 比 ‘2-point’ 更精确，但操作数量是其两倍。

示例

约束条件 x[0] < sin(x[1]) + 1.9

>>> from scipy.optimize import NonlinearConstraint
>>> import numpy as np
>>> con = lambda x: x[0] - np.sin(x[1])
>>> nlc = NonlinearConstraint(con, -np.inf, 1.9) 

scipy.optimize.LinearConstraint

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.LinearConstraint.html#scipy.optimize.LinearConstraint

class scipy.optimize.LinearConstraint(A, lb=-inf, ub=inf, keep_feasible=False)

变量的线性约束。

约束具有一般不等式形式：

lb <= A.dot(x) <= ub 

这里作为独立变量向量 x 以形状为(m,)的 ndarray 传递，矩阵 A 的形状为(m, n)。

可以使用相等的边界来表示等式约束或无穷边界来表示单侧约束。

参数：

A{array_like, 稀疏矩阵}，形状为(m, n)

定义约束的矩阵。

lb, ub稠密的数组，可选

约束的下限和上限。每个数组必须具有形状(m,)或者是标量，在后一种情况下，约束的所有组件都将具有相同的边界。使用np.inf和适当的符号来指定单侧约束。将lb和ub的组件设置相等以表示等式约束。请注意，可以通过根据需要设置lb和ub的不同组件来混合不同类型的约束：区间约束、单侧约束或等式约束。默认为lb = -np.inf和ub = np.inf（无限制）。

keep_feasible稠密的布尔数组，可选

是否在迭代过程中保持约束组件的可行性。单个值设置此属性以适用于所有组件。默认为 False。对于等式约束没有影响。

方法

residual(x)	计算约束函数与限制之间的残差

scipy.optimize.Bounds

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.Bounds.html#scipy.optimize.Bounds

class scipy.optimize.Bounds(lb=-inf, ub=inf, keep_feasible=False)

变量的边界约束。

约束条件具有一般的不等式形式：

lb <= x <= ub 

可以使用相等的边界表示等式约束或无穷大的边界表示单侧约束。

参数：

lb, ub稠密的数组，可选

自变量的下限和上限。lb、ub和keep_feasible必须具有相同的形状或可广播。将lb和ub的组件设为相等以固定变量。使用np.inf和适当的符号禁用所有或部分变量的边界。请注意，可以通过必要时设置lb和ub的不同组件来混合不同类型的约束：区间约束、单侧约束或等式约束。默认为lb = -np.inf和ub = np.inf（无边界）。

keep_feasible稠密的 bool 数组，可选

是否在迭代过程中保持约束组件的可行性。必须与lb和ub进行广播。默认为 False。对于等式约束无影响。

方法

residual(x)	计算输入与边界之间的残差（松弛度）

scipy.optimize.BFGS

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.BFGS.html#scipy.optimize.BFGS

class scipy.optimize.BFGS(exception_strategy='skip_update', min_curvature=None, init_scale='auto')

Broyden-Fletcher-Goldfarb-Shanno (BFGS) Hessian 更新策略。

参数:

exception_strategy{‘skip_update’, ‘damp_update’}, 可选

定义在曲率条件违反时如何进行。将其设置为 ‘skip_update’ 以跳过更新。或者，将其设置为 ‘damp_update’ 以在实际的 BFGS 结果和未修改的矩阵之间插值。这两种异常策略在 [1]，p.536-537 中有解释。

min_curvaturefloat

该数字乘以归一化因子，定义了允许不受异常策略影响的最小曲率 dot(delta_grad, delta_x)。当 exception_strategy = 'skip_update' 时，默认为 1e-8，当 exception_strategy = 'damp_update' 时，默认为 0.2。

init_scale{float, ‘auto’}

矩阵在第一次迭代时的尺度。在第一次迭代中，Hessian 矩阵或其逆将初始化为 init_scale*np.eye(n)，其中 n 是问题的维度。将其设置为 ‘auto’ 可以使用自动启发式方法选择初始尺度。该启发式方法在 [1]，p.143 中描述。默认使用 ‘auto’。

注意事项

更新基于 [1]，p.140 中的描述。

参考文献

[1] (1,2,3)

Nocedal, Jorge, and Stephen J. Wright. “数值优化” 第二版 (2006)。

方法

dot§	计算内部矩阵与给定向量的乘积。
get_matrix()	返回当前内部矩阵。
initialize(n, approx_type)	初始化内部矩阵。
update(delta_x, delta_grad)	更新内部矩阵。

scipy.optimize.SR1

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.SR1.html#scipy.optimize.SR1

class scipy.optimize.SR1(min_denominator=1e-08, init_scale='auto')

对称秩 1 Hessian 更新策略。

参数：

min_denominator浮点数

此数字通过归一化因子缩放，定义了更新中允许的最小分母大小。当条件违反时，我们会跳过更新。默认使用1e-8。

init_scale{浮点数, ‘auto’}，可选

在第一次迭代中，Hessian 矩阵或其逆将用init_scale*np.eye(n)初始化，其中n是问题的维度。将其设置为’auto’，以便使用自动启发式方法选择初始规模。该启发式方法在[1]，p.143 中描述。默认情况下使用’auto’。

注意

更新基于描述[1]，p.144-146。

参考文献

[1] (1,2)

Nocedal, Jorge, and Stephen J. Wright. “Numerical optimization” Second Edition (2006).

方法

dot§	计算内部矩阵与给定向量的乘积。
get_matrix()	返回当前内部矩阵。
initialize(n, approx_type)	初始化内部矩阵。
update(delta_x, delta_grad)	更新内部矩阵。

scipy.optimize.basinhopping

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.basinhopping.html#scipy.optimize.basinhopping

scipy.optimize.basinhopping(func, x0, niter=100, T=1.0, stepsize=0.5, minimizer_kwargs=None, take_step=None, accept_test=None, callback=None, interval=50, disp=False, niter_success=None, seed=None, *, target_accept_rate=0.5, stepwise_factor=0.9)

使用盆地跳跃算法寻找函数的全局最小值。

盆地跳跃是一种两阶段方法，结合了全局步进算法和每步的局部最小化。设计用于模仿原子簇能量最小化的自然过程，适用于具有“漏斗形但崎岖”的能量景观的类似问题 [5]。

由于步骤采取、步骤接受和最小化方法都是可定制的，因此该函数也可以用于实现其他两阶段方法。

参数：

funccallable f(x, *args)

要优化的函数。args 可以作为字典 minimizer_kwargs 的可选项传递。

x0array_like

初始猜测。

niter整数，可选

盆地跳跃迭代次数。将有 niter + 1 次局部最小化运行。

T浮点数，可选

接受或拒绝标准的“温度”参数。较高的“温度”意味着将接受更大的函数值跳跃。为了获得最佳结果，T 应与局部最小值之间的分离（在函数值上）相当。

stepsize浮点数，可选

用于随机位移的最大步长。

minimizer_kwargsdict，可选

要传递给本地最小化器 scipy.optimize.minimize 的额外关键字参数。一些重要的选项可能包括：

methodstr

最小化方法（例如 "L-BFGS-B"）

argstuple

传递给目标函数 (func) 及其导数（Jacobian、Hessian）的额外参数。

take_stepcallable take_step(x)，可选

用此例程替换默认的步进例程。默认的步进例程是坐标的随机位移，但其他步进算法可能对某些系统更好。take_step 可以选择具有属性 take_step.stepsize。如果存在此属性，则 basinhopping 将调整 take_step.stepsize 以尝试优化全局最小搜索。

accept_testcallable，accept_test(f_new=f_new, x_new=x_new, f_old=fold, x_old=x_old)，可选

定义一个测试，用于判断是否接受该步骤。这将与基于“温度”T的 Metropolis 测试一起使用。可以接受的返回值为 True、False 或"force accept"。如果任何测试返回 False，则拒绝该步骤。如果是后者，则这将覆盖任何其他测试以接受该步骤。例如，可以强制性地从basinhopping被困住的局部最小值中逃脱。

callback可调用对象，callback(x, f, accept)，可选

一个回调函数，将为找到的所有最小值调用。x和f是试探最小值的坐标和函数值，accept表示是否接受该最小值。例如，可以使用此功能保存找到的最低的 N 个最小值。此外，callback可以用于通过可选地返回 True 来指定用户定义的停止标准，以停止basinhopping程序运行。

interval整数，可选

用于定期更新stepsize的间隔

disp布尔值，可选

设置为 True 以打印状态消息

niter_success整数，可选

如果全局最小候选在此迭代次数内保持不变，则停止运行。

seed{None, 整数, numpy.random.Generator, numpy.random.RandomState}，可选

如果seed为 None（或np.random），则使用numpy.random.RandomState单例。如果seed是整数，则使用一个新的RandomState实例，并使用seed进行种子化。如果seed已经是Generator或RandomState实例，则直接使用该实例。指定seed以进行可重复的最小化。使用此种子生成的随机数仅影响默认的 Metropolis accept_test和默认的take_step。如果您提供自己的take_step和accept_test，并且这些函数使用随机数生成，则这些函数负责其随机数生成器的状态。

target_accept_rate浮点数，可选

用于调整stepsize的目标接受率。如果当前接受率大于目标，则增加stepsize。否则，减少stepsize。范围为(0, 1)。默认值为 0.5。

自版本 1.8.0 新增。

stepwise_factor浮点数，可选

stepsize在每次更新时乘以或除以此步进因子。范围为(0, 1)。默认值为 0.9。

自版本 1.8.0 新增。

返回：

resOptimizeResult

优化结果表示为OptimizeResult对象。重要属性包括：x 解数组，fun 解处函数值，以及 message 描述终止原因。所选最小化器在最低最小值处返回的OptimizeResult对象也包含在此对象中，并可通过lowest_optimization_result属性访问。参见OptimizeResult获取其他属性的描述。

另见

minimize

局部最小化函数对每个 basinhopping 步骤调用。minimizer_kwargs 被传递给此例程。

注意事项

Basin-hopping 是一种随机算法，旨在找到一个或多个变量的光滑标量函数的全局最小值[1] [2] [3] [4]。该算法在目前的形式下由 David Wales 和 Jonathan Doye 描述[2] www-wales.ch.cam.ac.uk/。

算法是迭代的，每个周期由以下特征组成

1. 坐标的随机扰动

2. 局部最小化

3. 基于最小化函数值接受或拒绝新坐标

此处使用的接受测试是标准 Monte Carlo 算法的 Metropolis 标准，尽管还有许多其他可能性[3]。

已证明该全局最小化方法对物理和化学中的各种问题非常高效。当函数具有由大障碍物分隔的多个极小值时特别有用。请参见Cambridge Cluster Database以获取主要使用 basin-hopping 优化的分子系统数据库。该数据库包括超过 300 个自由度的最小化问题。

有关 basin-hopping 的 Fortran 实现请参见自由软件程序GMIN。该实现包括上述过程的许多变体，包括更高级的步骤算法和替代接受标准。

对于随机全局优化，无法确定是否实际上找到了真正的全局最小值。作为一致性检查，可以从多个不同的随机起始点运行算法，以确保每个示例中找到的最低最小值已收敛到全局最小值。因此，默认情况下，basinhopping 将仅运行 niter 次迭代，并返回找到的最低最小值。用户需要确保这实际上是全局最小值。

选择 stepsize：这是 basinhopping 中的关键参数，取决于正在解决的问题。步长在每个维度中均匀选择，从 x0-stepsize 到 x0+stepsize 的区域内。理想情况下，它应与被优化函数的局部极小值之间（在参数值上的）典型分离可比较。basinhopping 将默认调整 stepsize 以找到最优值，但这可能需要多次迭代。如果设置一个合理的初始值给 stepsize，则可以更快地获得结果。

选择 T：参数 T 是 Metropolis 准则中使用的“温度”。如果 func(xnew) < func(xold)，则 Basin-hopping 步骤始终被接受。否则，它们将以以下概率被接受：

exp( -(func(xnew) - func(xold)) / T ) 

因此，为了获得最佳结果，T 应与局部极小值之间（在函数值上的）典型差异可比较。（“墙”高度对局部极小值无关紧要。）

如果 T 为 0，则算法变为单调 Basin-Hopping，其中所有增加能量的步骤都被拒绝。

0.12.0 版本中的新内容。

参考文献

[1]

Wales, David J. 2003, 能量景观，剑桥大学出版社，剑桥，英国。

[2] (1,2)

Wales, D J 和 Doye J P K, Lennard-Jones 簇的基态结构的全局优化：通过 Basin-Hopping 和包含多达 110 个原子的结构。《物理化学学报》，1997 年，101，5111。

[3] (1,2)

Li, Z. 和 Scheraga, H. A., 蛋白质折叠中的多极小问题的蒙特卡洛-最小化方法，《美国国家科学院院刊》，1987 年，84，6611。

[4]

Wales, D. J. 和 Scheraga, H. A., 簇、晶体和生物分子的全局优化，《科学》，1999 年，285，1368。

[5]

Olson, B., Hashmi, I., Molloy, K., 和 Shehu1, A., Basin Hopping 作为生物大分子特征化的一般和多功能优化框架，《人工智能进展》，2012 年卷（2012），文章 ID 674832，DOI:10.1155/2012/674832

例子

下面的例子是一个一维最小化问题，在抛物线上叠加了许多局部极小值。

>>> import numpy as np
>>> from scipy.optimize import basinhopping
>>> func = lambda x: np.cos(14.5 * x - 0.3) + (x + 0.2) * x
>>> x0 = [1.] 

盆地跳跃内部使用局部最小化算法。我们将使用参数minimizer_kwargs告诉盆地跳跃使用哪种算法以及如何设置该最小化器。此参数将传递给scipy.optimize.minimize。

>>> minimizer_kwargs = {"method": "BFGS"}
>>> ret = basinhopping(func, x0, minimizer_kwargs=minimizer_kwargs,
...                    niter=200)
>>> print("global minimum: x = %.4f, f(x) = %.4f" % (ret.x, ret.fun))
global minimum: x = -0.1951, f(x) = -1.0009 

接下来考虑一个二维最小化问题。此外，这次我们将使用梯度信息来显著加速搜索。

>>> def func2d(x):
...     f = np.cos(14.5 * x[0] - 0.3) + (x[1] + 0.2) * x[1] + (x[0] +
...                                                            0.2) * x[0]
...     df = np.zeros(2)
...     df[0] = -14.5 * np.sin(14.5 * x[0] - 0.3) + 2. * x[0] + 0.2
...     df[1] = 2. * x[1] + 0.2
...     return f, df 

我们还将使用不同的局部最小化算法。此外，我们必须告诉最小化器，我们的函数同时返回能量和梯度（雅可比矩阵）。

>>> minimizer_kwargs = {"method":"L-BFGS-B", "jac":True}
>>> x0 = [1.0, 1.0]
>>> ret = basinhopping(func2d, x0, minimizer_kwargs=minimizer_kwargs,
...                    niter=200)
>>> print("global minimum: x = [%.4f, %.4f], f(x) = %.4f" % (ret.x[0],
...                                                           ret.x[1],
...                                                           ret.fun))
global minimum: x = [-0.1951, -0.1000], f(x) = -1.0109 

下面是一个使用自定义步进例程的示例。想象一下，你希望第一个坐标采取比其他坐标更大的步骤。可以这样实现：

>>> class MyTakeStep:
...    def __init__(self, stepsize=0.5):
...        self.stepsize = stepsize
...        self.rng = np.random.default_rng()
...    def __call__(self, x):
...        s = self.stepsize
...        x[0] += self.rng.uniform(-2.*s, 2.*s)
...        x[1:] += self.rng.uniform(-s, s, x[1:].shape)
...        return x 

由于MyTakeStep.stepsize存在，盆地跳跃将调整stepsize的大小以优化搜索。我们将使用与之前相同的二维函数。

>>> mytakestep = MyTakeStep()
>>> ret = basinhopping(func2d, x0, minimizer_kwargs=minimizer_kwargs,
...                    niter=200, take_step=mytakestep)
>>> print("global minimum: x = [%.4f, %.4f], f(x) = %.4f" % (ret.x[0],
...                                                           ret.x[1],
...                                                           ret.fun))
global minimum: x = [-0.1951, -0.1000], f(x) = -1.0109 

现在，让我们使用一个自定义回调函数的示例，该函数打印出每个找到的最小值的值。

>>> def print_fun(x, f, accepted):
...         print("at minimum %.4f accepted %d" % (f, int(accepted))) 

这次我们只运行 10 次盆地跳步。

>>> rng = np.random.default_rng()
>>> ret = basinhopping(func2d, x0, minimizer_kwargs=minimizer_kwargs,
...                    niter=10, callback=print_fun, seed=rng)
at minimum 0.4159 accepted 1
at minimum -0.4317 accepted 1
at minimum -1.0109 accepted 1
at minimum -0.9073 accepted 1
at minimum -0.4317 accepted 0
at minimum -0.1021 accepted 1
at minimum -0.7425 accepted 1
at minimum -0.9073 accepted 1
at minimum -0.4317 accepted 0
at minimum -0.7425 accepted 1
at minimum -0.9073 accepted 1 

在第 8 次迭代中已经找到的最小值为-1.0109，实际上是全局最小值。

scipy.optimize.brute

原文：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.brute.html#scipy.optimize.brute

scipy.optimize.brute(func, ranges, args=(), Ns=20, full_output=0, finish=<function fmin>, disp=False, workers=1)

通过蛮力法在给定范围内最小化一个函数。

使用“蛮力”方法，即在多维点网格的每个点计算函数的值，以找到函数的全局最小值。

函数在调用时以第一个调用函数的数据类型在范围内进行评估，由 vectorize NumPy 函数强制执行。当 full_output=True 时，函数评估的值和类型受 finish 参数的影响（详见 Notes）。

蛮力法是低效的，因为网格点的数量呈指数增长 - 要评估的网格点数量为 Ns ** len(x)。因此，即使是粗略的网格间距，中等规模的问题也可能需要很长时间运行，或者会遇到内存限制。

参数：

funccallable

要最小化的目标函数。必须是形式为 f(x, *args) 的函数，其中 x 是一个一维数组的参数，而 args 是一个元组，包含完全指定函数所需的任何额外固定参数。

rangestuple

ranges 元组的每个组件必须是“切片对象”或形如 (low, high) 的范围元组。程序使用这些来创建网格点，以便计算目标函数。详见 Note 2。

argstuple, optional

任何额外固定参数，以完全指定函数。

Nsint, optional

如果未另有说明，每个轴上的网格点数。详见 Note2。

full_outputbool, optional

如果为 True，则返回评估网格及其上的目标函数值。

finishcallable, optional

一个优化函数，它以蛮力最小化的结果作为初始猜测进行调用。finish 应将 func 和初始猜测作为位置参数，并将 args 作为关键字参数。它还可以作为关键字参数接受 full_output 和/或 disp。如果不使用“抛光”函数，则使用 None。详见 Notes 获取更多详情。

dispbool, optional

设置为 True 时，打印来自 finish 可调用的收敛消息。

workersint or map-like callable, optional

如果 workers 是一个整数，则将网格细分为 workers 部分，并并行评估（使用 multiprocessing.Pool）。提供 -1 使用所有可用的核心进程。或者提供一个类似映射的可调用对象，例如 multiprocessing.Pool.map 用于并行评估网格。此评估是作为 workers(func, iterable) 进行的。要求 func 可被 pickle。

自版本 1.3.0 起新增。

返回：

x0ndarray

包含目标函数取得其最小值的点的坐标的一维数组。（参见注 1，了解返回的是哪个点。）

fval浮点数

x0点处的函数值。（当full_output为 True 时返回。）

grid元组

评估网格的表示。它与x0的长度相同。（当full_output为 True 时返回。）

Jout数组

在评估网格的每个点处的函数值，即Jout = func(*grid)。（当full_output为 True 时返回。）

另请参见

basinhopping，differential_evolution

笔记

注 1：程序找到了目标函数取得最低值的网格点。如果finish为 None，则返回该点。当全局最小值出现在网格边界内（或者非常接近）且网格足够精细时，该点将位于全局最小值的邻近区域。

然而，用户通常使用其他优化程序来“磨光”网格点的值，即在brute的最佳网格点附近寻找更精确（局部）的最小值。brute函数的finish选项提供了一种方便的方法来实现此目的。使用的任何磨光程序必须将brute的输出作为其位置参数的初始猜测，并将brute的输入值作为关键字参数的args。否则将会引发错误。它还可以作为关键字参数接受full_output和/或disp。

brute假设finish函数返回OptimizeResult对象或形如(xmin, Jmin, ... , statuscode)的元组，其中xmin是参数的最小值，Jmin是目标函数的最小值，“…”可能是其他返回的值（brute不使用），而statuscode是finish程序的状态码。

注意，当finish不为 None 时，返回的值是finish程序的结果，而不是网格点的结果。因此，虽然brute限制其搜索在输入网格点上，但finish程序的结果通常不会与任何网格点重合，并且可能落在网格的边界之外。因此，如果仅需要在提供的网格点上找到最小值，请确保传入finish=None。

注 2：点的网格是一个numpy.mgrid对象。对于brute，ranges和Ns的输入具有以下效果。ranges元组的每个组件可以是一个切片对象或一个给定值范围的两元组，比如(0, 5)。如果组件是一个切片对象，brute直接使用它。如果组件是一个两元组范围，brute内部将其转换为一个切片对象，该对象从其低值到其高值插值出Ns个点，包括两端的值。

例子

我们演示了使用brute来寻找一个由正定二次型和两个深“高斯形”坑的函数的全局最小值。具体地，定义目标函数f为另外三个函数的和，f = f1 + f2 + f3。我们假设每个函数都有一个签名(z, *params)，其中z = (x, y)，而params和函数如下所定义。

>>> import numpy as np
>>> params = (2, 3, 7, 8, 9, 10, 44, -1, 2, 26, 1, -2, 0.5)
>>> def f1(z, *params):
...     x, y = z
...     a, b, c, d, e, f, g, h, i, j, k, l, scale = params
...     return (a * x**2 + b * x * y + c * y**2 + d*x + e*y + f) 

>>> def f2(z, *params):
...     x, y = z
...     a, b, c, d, e, f, g, h, i, j, k, l, scale = params
...     return (-g*np.exp(-((x-h)**2 + (y-i)**2) / scale)) 

>>> def f3(z, *params):
...     x, y = z
...     a, b, c, d, e, f, g, h, i, j, k, l, scale = params
...     return (-j*np.exp(-((x-k)**2 + (y-l)**2) / scale)) 

>>> def f(z, *params):
...     return f1(z, *params) + f2(z, *params) + f3(z, *params) 

因此，目标函数可能在由其组成的三个函数的最小值附近有局部极小值。为了使用fmin来优化其格点结果，我们可以继续如下操作：

>>> rranges = (slice(-4, 4, 0.25), slice(-4, 4, 0.25))
>>> from scipy import optimize
>>> resbrute = optimize.brute(f, rranges, args=params, full_output=True,
...                           finish=optimize.fmin)
>>> resbrute[0]  # global minimum
array([-1.05665192,  1.80834843])
>>> resbrute[1]  # function value at global minimum
-3.4085818767 

请注意，如果finish被设置为 None，我们将得到格点[-1.0 1.75]，其中四舍五入的函数值为-2.892。

scipy.optimize.differential_evolution

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.differential_evolution.html#scipy.optimize.differential_evolution

scipy.optimize.differential_evolution(func, bounds, args=(), strategy='best1bin', maxiter=1000, popsize=15, tol=0.01, mutation=(0.5, 1), recombination=0.7, seed=None, callback=None, disp=False, polish=True, init='latinhypercube', atol=0, updating='immediate', workers=1, constraints=(), x0=None, *, integrality=None, vectorized=False)

找到多元函数的全局最小值。

差分进化方法[1]具有随机性质。它不使用梯度方法来找到最小值，可以搜索候选空间的大面积，但通常需要比传统的基于梯度的技术更多的函数评估次数。

算法是由斯托恩和普赖斯[2]提出的。

参数：

func可调用

要最小化的目标函数。必须以 f(x, *args) 的形式存在，其中 x 是形式为 1-D 数组的参数，args 是任何额外的固定参数元组，用于完全指定函数。参数数量 N 等于 len(x)。

bounds序列或Bounds

变量的边界。有两种指定边界的方式：

1. Bounds 类的实例。
3. (min, max)对，用于定义 func 优化参数 x 的有限下限和上限。

使用总边界数来确定参数数量 N。如果有参数的边界相等，则自由参数的总数为 N - N_equal。

args元组，可选

用于完全指定目标函数的任何额外固定参数。

strategy{str, 可调用}，可选

使用的差分进化策略。应为以下之一：

• ‘best1bin’
• ‘best1exp’
• ‘rand1bin’
• ‘rand1exp’
• ‘rand2bin’
• ‘rand2exp’
• ‘randtobest1bin’
• ‘randtobest1exp’
• ‘currenttobest1bin’
• ‘currenttobest1exp’
• ‘best2exp’
• ‘best2bin’

默认为‘best1bin’。可以实施的策略在‘Notes’中有概述。另外，差分进化策略可以通过提供一个构建试验向量的可调用对象来进行定制化。该可调用对象必须具有形式strategy(candidate: int, population: np.ndarray, rng=None)，其中candidate是一个整数，指定要进化的种群条目，population是形状为(S, N)的数组，包含所有种群成员（其中 S 是总种群大小），rng是求解器内使用的随机数生成器。candidate的范围为[0, S)。strategy必须返回一个形状为*(N,)*的试验向量。将此试验向量的适应度与population[candidate]的适应度进行比较。

自版本 1.12.0 起更改：通过可调用对象定制进化策略。

maxiterint，可选

演化整个种群的最大代数。没有优化的最大函数评估次数为：(maxiter + 1) * popsize * (N - N_equal)。

popsizeint, optional

用于设置总种群大小的乘数。种群包含popsize * (N - N_equal)个个体。如果通过init关键字提供了初始种群，则此关键字将被覆盖。使用init='sobol'时，种群大小计算为popsize * (N - N_equal)后的下一个 2 的幂。

tolfloat, optional

收敛的相对容差，当np.std(pop) <= atol + tol * np.abs(np.mean(population_energies))时停止求解，其中atol和tol分别为绝对容差和相对容差。

mutationfloat or tuple(float, float), optional

变异常数。在文献中，这也被称为差分权重，用 F 表示。如果指定为浮点数，则应在[0, 2]范围内。如果指定为元组(min, max)，则采用抖动。抖动会随机地在每代基础上改变变异常数。该代的变异常数取自U[min, max)。抖动可以显著加快收敛速度。增加变异常数会增加搜索半径，但会减慢收敛速度。

recombinationfloat, optional

重组常数，应在[0, 1]范围内。在文献中，这也被称为交叉概率，用 CR 表示。增加此值允许更多的突变体进入下一代，但会有种群稳定性的风险。

seed{None, int, numpy.random.Generator, numpy.random.RandomState}, optional

如果seed为 None（或np.random），则使用numpy.random.RandomState单例。如果seed为整数，则使用一个新的RandomState实例，并用seed进行种子化。如果seed已经是Generator或RandomState实例，则使用该实例。为了重复最小化操作，请指定seed。

dispbool, optional

每次迭代时打印评估的func。

callbackcallable, optional

每次迭代后调用的可调用对象，具有以下签名：

callback(intermediate_result: OptimizeResult)。

其中intermediate_result是一个包含OptimizeResult属性x和fun的关键字参数，表示到目前为止找到的最佳解和目标函数值。请注意，回调函数必须传递一个名为intermediate_result的OptimizeResult。

回调还支持类似的签名：

callback(x, convergence: float=val)

val表示种群收敛的分数值。当val大于1.0时，函数停止。

使用内省来确定调用的签名之一。

全局最小化将在回调引发StopIteration或返回True时终止；仍会执行任何调整。

在版本 1.12.0 中更改：回调接受intermediate_result关键字。

polishbool，可选

如果为 True（默认），则最后使用L-BFGS-B方法的scipy.optimize.minimize来优化最佳种群成员，这可能会略微改善最小化。如果正在研究受约束问题，则改为使用trust-constr方法。对于具有许多约束的大问题，由于雅可比计算，优化可能需要很长时间。

initstr 或类数组，可选

指定执行的种群初始化类型。应为以下之一：

• ‘latinhypercube’
• ‘sobol’
• ‘halton’
• ‘random’
• 数组指定初始种群。数组应具有形状(S, N)，其中 S 为总种群大小，N 为参数数量。在使用之前，init将被剪辑到bounds内。

默认为‘latinhypercube’。拉丁超立方体采样试图最大化可用参数空间的覆盖。

‘sobol’和‘halton’是更优的选择，甚至更大程度地最大化参数空间。‘sobol’将强制初始种群大小计算为popsize * (N - N_equal)后的下一个 2 的幂。‘halton’没有要求，但效率稍低。有关更多详情，请参见scipy.stats.qmc。

‘random’随机初始化种群 - 这样做的缺点是可能会发生聚类，从而阻止参数空间的整体覆盖。例如，可以使用数组来指定种群，以在已知解存在的位置创建一组紧密的初始猜测，从而减少收敛时间。

atolfloat，可选

收敛的绝对容差，当np.std(pop) <= atol + tol * np.abs(np.mean(population_energies))时，求解停止，其中atol和tol分别是绝对容差和相对容差。

updating{‘immediate’, ‘deferred’}, optional

如果是'immediate'，则最佳解向量在单一生成过程中持续更新[4]。这可以加快收敛速度，因为试验向量可以利用最佳解的持续改进。如果是'deferred'，则最佳解向量每代更新一次。只有'deferred'与并行化或向量化兼容，且workers和vectorized关键字可以覆盖此选项。

自 1.2.0 版新增。

工作者int 或类似映射的可调用对象，可选

如果workers是整数，则将种群细分为workers部分，并并行评估（使用multiprocessing.Pool）。提供-1 以使用所有可用 CPU 核心。或者提供类似映射的可调用对象，例如multiprocessing.Pool.map以并行评估种群。此评估以workers(func, iterable)进行。如果workers != 1，此选项将覆盖updating关键字为updating='deferred'。如果workers != 1，此选项将覆盖vectorized关键字。要求func可 pickle 化。

自 1.2.0 版新增。

约束条件{非线性约束，线性约束，边界}

解算器的约束条件，除了bounds kwd 应用的约束外。使用 Lampinen 的方法[5]。

自 1.4.0 版新增。

x0None 或类似数组，可选

提供最小化的初始猜测。一旦种群被初始化，此向量替换第一个（最佳）成员。即使init给出了初始种群，也会进行此替换。x0.shape == (N,)。

自 1.7.0 版新增。

整数性1-D 数组，可选

对于每个决策变量，一个布尔值，指示决策变量是否约束为整数值。该数组广播到(N,)。如果有任何决策变量被约束为整数，则在精炼过程中它们不会改变。只使用介于下限和上限之间的整数值。如果在边界之间没有整数值，则会引发ValueError。

自 1.9.0 版新增。

向量化bool，可选

如果vectorized为 True，则将使用形状为(N, S)的x数组发送给func，并期望返回一个形状为(S,)的数组，其中S是要计算的解向量数量。如果应用了约束条件，则用于构建Constraint对象的每个函数应接受形状为(N, S)的x数组，并返回形状为(M, S)的数组，其中M是约束组件的数量。这个选项是workers提供的并行化的替代方案，并且可以通过减少从多个函数调用中的解释器开销来提高优化速度。如果workers != 1，则将忽略此关键字。此选项将覆盖updating关键字为updating='deferred'。有关何时使用'vectorized'和何时使用'workers'的进一步讨论，请参见备注部分。

新版本 1.9.0 中的更新。

返回：

resOptimizeResult

优化结果表示为OptimizeResult对象。重要属性包括：x解向量数组，success布尔标志，指示优化器是否成功退出，message描述终止原因，population种群中的解向量以及population_energies每个population条目的目标函数值。有关其他属性的描述，请参见OptimizeResult。如果使用了polish，并且通过打磨获得了更低的最小值，则 OptimizeResult 还包含jac属性。如果最终解决方案不满足应用的约束条件，则success将为False。

备注

差分进化是一种基于随机种群的方法，适用于全局优化问题。在每次种群遍历过程中，算法通过与其他候选解混合来生成一个试验候选解，对每个候选解进行突变。有几种策略[3]用于创建试验候选解，适用于不同的问题。"best1bin"策略对许多系统而言是一个良好的起点。在这种策略中，随机选择种群中的两个成员。他们的差异用于突变迄今为止最佳成员（"best"在"best1bin"中的意思），(x_0)：

[b’ = x_0 + mutation * (x_{r_0} - x_{r_1})]

然后构造一个试验向量。从随机选择的第 i 个参数开始，依次用来自b'或原始候选者的参数填充（取模）。使用b'或原始候选者的选择是通过二项分布（‘best1bin’中的’bin’）进行的 - 生成一个介于[0, 1)的随机数。如果此数小于recombination常数，则参数从b'加载，否则从原始候选者加载。最后一个参数始终从b'加载。构建完试验候选者后，评估其适应度。如果试验结果比原始候选者好，则替换它。如果它还优于整体最佳候选者，则也替换该候选者。

其他可用的策略见 Qiang 和 Mitchell（2014）[3]。

[ \begin{align}\begin{aligned}rand1* : b’ = x_{r_0} + mutation*(x_{r_1} - x_{r_2})\rand2* : b’ = x_{r_0} + mutation*(x_{r_1} + x_{r_2} - x_{r_3} - x_{r_4})\best1* : b’ = x_0 + mutation*(x_{r_0} - x_{r_1})\best2* : b’ = x_0 + mutation*(x_{r_0} + x_{r_1} - x_{r_2} - x_{r_3})\currenttobest1* : b’ = x_i + mutation*(x_0 - x_i + x_{r_0} - x_{r_1})\randtobest1* : b’ = x_{r_0} + mutation*(x_0 - x_{r_0} + x_{r_1} - x_{r_2})\end{aligned}\end{align} ]

其中整数(r_0, r_1, r_2, r_3, r_4)从区间[0, NP)随机选择，其中NP是总体大小，原始候选者索引为i。用户可以通过向strategy提供可调用对象来完全自定义试验候选者的生成方式。

要提高找到全局最小值的机会，可以使用更高的popsize值，更高的mutation值和（抖动），但更低的recombination值。这样做会扩大搜索半径，但会减慢收敛速度。

默认情况下，最佳解向量在单次迭代中持续更新（updating='immediate'）。这是对原始差分进化算法的修改[4]，可以使试验向量立即从改进的解决方案中获益。要使用斯托恩和普莱斯的原始行为，即每次迭代更新一次最佳解，设置updating='deferred'。'deferred'方法既兼容并行化和矢量化（'workers'和'vectorized'关键字）。这些方法可能通过更有效地利用计算资源来提高最小化速度。'workers'将计算分布到多个处理器上。默认情况下，Python 的multiprocessing模块用于此，但也可以使用其他方法，例如在集群上使用消息传递接口（MPI）[6] [7]。这些方法（创建新进程等）可能会带来一定的开销，这意味着计算速度并不一定随使用处理器数量的增加而线性扩展。并行化最适合计算密集型目标函数。如果目标函数较为简单，则'vectorized'可能会有所帮助，因为它每次迭代仅调用一次目标函数，而不是为所有种群成员多次调用；解释器开销减少。

0.15.0 版新增内容。

参考文献

[1]

差分进化，维基百科，en.wikipedia.org/wiki/Differential_evolution

[2]

斯托恩（Storn, R）和普莱斯（Price, K），差分进化 - 一种简单高效的连续空间全局优化启发式算法，全球优化期刊，1997 年，11，341 - 359。

[3] (1,2)

强（Qiang, J.），米切尔（Mitchell, C.），统一差分进化算法用于全局优化，2014 年，www.osti.gov/servlets/purl/1163659

[4] (1,2)

沃明顿（Wormington, M.），帕纳乔内（Panaccione, C.），马特尼（Matney, K. M.），鲍文（Bowen, D. K.），利用遗传算法从 X 射线散射数据中表征结构，伦敦皇家学会 A 类学报，1999 年，357，2827-2848

[5]

兰皮宁（Lampinen, J.），差分进化算法的约束处理方法。2002 年进化计算大会论文集。CEC’02（Cat. No. 02TH8600）。第 2 卷。IEEE，2002 年。

[6]

mpi4py.readthedocs.io/en/stable/

[7]

schwimmbad.readthedocs.io/en/latest/

例子

让我们考虑最小化 Rosenbrock 函数的问题。这个函数在 rosen 中实现于 scipy.optimize。

>>> import numpy as np
>>> from scipy.optimize import rosen, differential_evolution
>>> bounds = [(0,2), (0, 2), (0, 2), (0, 2), (0, 2)]
>>> result = differential_evolution(rosen, bounds)
>>> result.x, result.fun
(array([1., 1., 1., 1., 1.]), 1.9216496320061384e-19) 

现在重复，但使用并行化。

>>> result = differential_evolution(rosen, bounds, updating='deferred',
...                                 workers=2)
>>> result.x, result.fun
(array([1., 1., 1., 1., 1.]), 1.9216496320061384e-19) 

让我们进行有约束的最小化。

>>> from scipy.optimize import LinearConstraint, Bounds 

我们增加约束条件，即 x[0] 和 x[1] 的和必须小于或等于 1.9。这是一个线性约束，可以写成 A @ x <= 1.9，其中 A = array([[1, 1]])。这可以编码为 LinearConstraint 实例：

>>> lc = LinearConstraint([[1, 1]], -np.inf, 1.9) 

使用 Bounds 对象指定限制。

>>> bounds = Bounds([0., 0.], [2., 2.])
>>> result = differential_evolution(rosen, bounds, constraints=lc,
...                                 seed=1)
>>> result.x, result.fun
(array([0.96632622, 0.93367155]), 0.0011352416852625719) 

寻找 Ackley 函数的最小值（en.wikipedia.org/wiki/Test_functions_for_optimization）。

>>> def ackley(x):
...     arg1 = -0.2 * np.sqrt(0.5 * (x[0] ** 2 + x[1] ** 2))
...     arg2 = 0.5 * (np.cos(2. * np.pi * x[0]) + np.cos(2. * np.pi * x[1]))
...     return -20. * np.exp(arg1) - np.exp(arg2) + 20. + np.e
>>> bounds = [(-5, 5), (-5, 5)]
>>> result = differential_evolution(ackley, bounds, seed=1)
>>> result.x, result.fun
(array([0., 0.]), 4.440892098500626e-16) 

Ackley 函数以矢量化方式编写，因此可以使用 'vectorized' 关键字。请注意减少的函数评估次数。

>>> result = differential_evolution(
...     ackley, bounds, vectorized=True, updating='deferred', seed=1
... )
>>> result.x, result.fun
(array([0., 0.]), 4.440892098500626e-16) 

以下自定义策略函数模仿 ‘best1bin’：

>>> def custom_strategy_fn(candidate, population, rng=None):
...     parameter_count = population.shape(-1)
...     mutation, recombination = 0.7, 0.9
...     trial = np.copy(population[candidate])
...     fill_point = rng.choice(parameter_count)
...
...     pool = np.arange(len(population))
...     rng.shuffle(pool)
...
...     # two unique random numbers that aren't the same, and
...     # aren't equal to candidate.
...     idxs = []
...     while len(idxs) < 2 and len(pool) > 0:
...         idx = pool[0]
...         pool = pool[1:]
...         if idx != candidate:
...             idxs.append(idx)
...
...     r0, r1 = idxs[:2]
...
...     bprime = (population[0] + mutation *
...               (population[r0] - population[r1]))
...
...     crossovers = rng.uniform(size=parameter_count)
...     crossovers = crossovers < recombination
...     crossovers[fill_point] = True
...     trial = np.where(crossovers, bprime, trial)
...     return trial 

scipy.optimize.shgo

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.shgo.html#scipy.optimize.shgo

scipy.optimize.shgo(func, bounds, args=(), constraints=None, n=100, iters=1, callback=None, minimizer_kwargs=None, options=None, sampling_method='simplicial', *, workers=1)

使用 SHG 优化找到函数的全局最小值。

SHGO 代表“单纯同调全局优化”。

参数：

func可调用

要最小化的目标函数。必须以f(x, *args)形式，其中x是一个 1-D 数组的参数，而args是完全指定函数所需的额外固定参数的元组。

bounds序列或Bounds

变量的边界。有两种指定边界的方法：

1. Bounds类的实例。

2. x的每个元素的(min, max)对的序列。

args元组，可选

任何完全指定目标函数所需的额外固定参数。

constraints{约束，字典}或约束列表，可选

约束定义。仅适用于 COBYLA、SLSQP 和 trust-constr。参见教程[5]以了解有关指定约束的详细信息。

注意

目前仅 COBYLA、SLSQP 和 trust-constr 局部最小化方法支持约束参数。如果在本地优化问题中使用的constraints序列未在minimizer_kwargs中定义，并且使用了约束方法，则将使用全局的constraints（在minimizer_kwargs中定义了constraints序列意味着不会添加constraints，因此如果需要添加等式约束等等，则需要将约束函数添加到minimizer_kwargs中的不等式函数中）。COBYLA 仅支持不等式约束。

从版本 1.11.0 起：constraints接受NonlinearConstraint，LinearConstraint。

n整数，可选

在构建单纯复合物时使用的采样点数。对于默认的simplicial采样方法，生成 2**dim + 1 个采样点，而不是默认的n=100。对于所有其他指定的值，生成n个采样点。对于sobol、halton和其他任意的sampling_methods，生成n=100或另一个指定的采样点数。

iters整数，可选

用于构建单纯复合物的迭代次数。默认为 1。

callback可调用，可选

在每次迭代后调用，形式为callback(xk)，其中xk是当前参数向量。

minimizer_kwargs字典，可选

要传递给最小化器scipy.optimize.minimize的额外关键字参数。一些重要的选项可能是：

• methodstr

• 最小化方法。如果未指定，则根据问题是否有约束或边界选择为 BFGS、L-BFGS-B、SLSQP 之一。

• argstuple

• 传递给目标函数 (func) 及其导数（Jacobian、Hessian）的额外参数。

• 选项字典，可选

• 注意，默认情况下容差被指定为 {ftol: 1e-12}

选项字典，可选

解算器选项字典。许多指定给全局例程的选项也传递给 scipy.optimize.minimize 例程。传递给局部例程的选项标有“(L)”。

停止标准，如果满足任何指定的准则则算法将终止。但是，默认算法不需要指定任何准则：

• maxfevint (L)

  可行域内的最大函数评估次数。（注意，只有支持此选项的方法才会精确地在指定值处终止例程。否则，准则只会在全局迭代期间终止）

• f_min

  如果已知，指定最小目标函数值。

• f_tolfloat

  值 f 的停止准则的精度目标。请注意，如果全局例程中的采样点在此容差内，则全局例程也将终止。

• maxiterint

  执行的最大迭代次数。

• maxevint

  最大采样评估次数（包括在不可行点中的搜索）。

• maxtimefloat

  允许的最大处理运行时

• minhgrdint

  最小同调群秩差分。在每次迭代期间（大约）计算目标函数的同调群。该群的秩与目标函数中局部凸子域的数量具有一一对应关系（在足够的采样点后，这些子域包含唯一的全局最小值）。如果指定迭代的 maxhgrd 中 hgr 的差异为 0，则算法将终止。

目标函数知识：

• 对称性列表或布尔值

  指定目标函数是否包含对称变量。在完全对称的情况下，搜索空间（因此性能）最多减少 O(n!) 倍。如果指定为 True，则所有变量将被设置为相对于第一个变量对称。默认设置为 False。

  例如，f(x) = (x_1 + x_2 + x_3) + (x_4)**2 + (x_5)**2 + (x_6)**2

  在此方程中，x_2 和 x_3 对 x_1 对称，而 x_5 和 x_6 对 x_4 对称，可以指定给解算器如下：

  对称性 = [0, # 变量 1

  0, # 对变量 1 对称 0, # 对变量 1 3, # 变量 4 3, # 对变量 4 3, # 对变量 4 ]

• jacbool 或可调用，可选

  目标函数的 Jacobian（梯度）。仅适用于 CG、BFGS、Newton-CG、L-BFGS-B、TNC、SLSQP、dogleg 和 trust-ncg。如果jac为布尔值且为 True，则假定fun返回目标函数的梯度。如果为 False，则梯度将以数值方式估计。jac也可以是一个返回目标函数梯度的可调用对象。在这种情况下，它必须接受与fun相同的参数。（将自动传递给scipy.optimize.minimize）

• hess，hesspcallable，可选

  Hessian（二阶导数矩阵）的目标函数或者目标函数的 Hessian 乘以任意向量 p。仅适用于 Newton-CG、dogleg 和 trust-ncg。hessp或hess中只需提供一个。如果提供了hess，则将忽略hessp。如果hess和hessp都未提供，则将在jac上使用有限差分近似 Hessian 乘积。hessp必须计算 Hessian 乘以任意向量。（将自动传递给scipy.optimize.minimize）

算法设置：

• minimize_every_iterbool

  如果为 True，则有前景的全局采样点将传递给每次迭代的本地最小化程序。如果为 False，则仅运行最终的最小化池。默认为 True。

• local_iterint

  每次迭代仅评估少数最佳最小化候选点。如果为 False，则所有潜在点都将传递给本地最小化程序。

• infty_constraintsbool

  如果为 True，则生成的任何采样点超出可行域将被保存，并给予目标函数值inf。如果为 False，则这些点将被丢弃。使用此功能可以在找到全局最小值之前提高函数评估的性能。指定为 False 将以稍微降低性能的代价节省内存。默认为 True。

反馈：

• dispbool（L）

  设置为 True 以打印收敛消息。

sampling_methodstr 或函数，可选

当前内置的采样方法选项为halton、sobol和simplicial。默认的simplicial提供了有限时间内收敛到全局最小值的理论保证。halton和sobol方法在采样点生成方面更快，但失去了保证收敛性。对于大多数“较简单”的问题，这更为适用。用户定义的采样函数必须每次调用接受n个维度为dim的采样点，并输出形状为n x dim的采样点数组。

workersint 或类似映射的可调用对象，可选

并行地对样本进行本地串行最小化。提供-1 以使用所有可用的 CPU 核心，或提供一个整数以使用这么多进程（使用multiprocessing.Pool）。

或者提供一个类似映射的可调用对象，例如multiprocessing.Pool.map以进行并行评估。此评估以workers(func, iterable)形式进行。要求func可被 pickle。

从版本 1.11.0 开始新增。

返回：

resOptimizeResult

优化结果表示为OptimizeResult对象。重要属性包括：x是对应全局最小值的解数组，fun是全局解处的函数输出，xl是局部最小解的排序列表，funl是相应局部解的函数输出，success是一个布尔标志，指示优化器是否成功退出，message描述终止原因，nfev是包括采样调用在内的总目标函数评估次数，nlfev是所有局部搜索优化导致的总目标函数评估次数，nit是全局例程执行的迭代次数。

注释

使用单纯同调全局优化进行全局优化 [1]。适用于解决通用 NLP 和黑盒优化问题以达到全局最优（低维问题）。

一般来说，优化问题的形式为：

minimize f(x) subject to

g_i(x) >= 0,  i = 1,...,m
h_j(x)  = 0,  j = 1,...,p 

这里 x 是一个或多个变量的向量。f(x)是目标函数R^n -> R，g_i(x)是不等式约束，h_j(x)是等式约束。

可选地，还可以使用bounds参数指定 x 中每个元素的下限和上限。

虽然 SHGO 的大部分理论优势仅对f(x)为 Lipschitz 光滑函数时得到证明，但是当f(x)是非连续、非凸且非光滑时，如果使用默认的采样方法，该算法也被证明能够收敛到全局最优解 [1]。

可以使用minimizer_kwargs参数指定本地搜索方法，该参数传递给scipy.optimize.minimize。默认情况下使用SLSQP方法。一般建议如果问题定义了不等式约束，则使用SLSQP或COBYLA本地最小化方法，因为其他方法不使用约束。

使用scipy.stats.qmc生成halton和sobol方法点。还可以使用任何其他 QMC 方法。

参考文献

[1] (1,2)

Endres, SC, Sandrock, C, Focke, WW (2018) “一种用于 Lipschitz 优化的单纯同调算法”，全球优化期刊。

[2]

Joe, SW 和 Kuo, FY（2008）“用更好的二维投影构建 Sobol 序列”，SIAM J. Sci. Comput. 30, 2635-2654。

[3] (1,2)

Hock, W 和 Schittkowski, K（1981）“非线性规划代码的测试示例”，经济与数学系统讲义，187. Springer-Verlag，纽约。www.ai7.uni-bayreuth.de/test_problem_coll.pdf

[4]

Wales, DJ（2015）“观点：从势能景观中获取反应坐标和动态的洞察”，化学物理学杂志，142(13), 2015。

[5]

docs.scipy.org/doc/scipy/tutorial/optimize.html#constrained-minimization-of-multivariate-scalar-functions-minimize

示例

首先考虑最小化 Rosenbrock 函数的问题，rosen：

>>> from scipy.optimize import rosen, shgo
>>> bounds = [(0,2), (0, 2), (0, 2), (0, 2), (0, 2)]
>>> result = shgo(rosen, bounds)
>>> result.x, result.fun
(array([1., 1., 1., 1., 1.]), 2.920392374190081e-18) 

注意，边界确定目标函数的维度，因此是必需的输入，但是您可以使用None或类似np.inf的对象指定空边界，这些将被转换为大的浮点数。

>>> bounds = [(None, None), ]*4
>>> result = shgo(rosen, bounds)
>>> result.x
array([0.99999851, 0.99999704, 0.99999411, 0.9999882 ]) 

接下来，我们考虑 Eggholder 函数，这是一个具有多个局部极小值和一个全局极小值的问题。我们将演示shgo的参数使用和能力。

>>> import numpy as np
>>> def eggholder(x):
...     return (-(x[1] + 47.0)
...             * np.sin(np.sqrt(abs(x[0]/2.0 + (x[1] + 47.0))))
...             - x[0] * np.sin(np.sqrt(abs(x[0] - (x[1] + 47.0))))
...             )
...
>>> bounds = [(-512, 512), (-512, 512)] 

shgo具有内置的低差异采样序列。首先，我们将输入*Sobol’*序列的 64 个初始采样点：

>>> result = shgo(eggholder, bounds, n=64, sampling_method='sobol')
>>> result.x, result.fun
(array([512\.        , 404.23180824]), -959.6406627208397) 

shgo还返回了找到的任何其他局部极小值，可以使用以下方式调用：

>>> result.xl
array([[ 512\.        ,  404.23180824],
 [ 283.0759062 , -487.12565635],
 [-294.66820039, -462.01964031],
 [-105.87688911,  423.15323845],
 [-242.97926   ,  274.38030925],
 [-506.25823477,    6.3131022 ],
 [-408.71980731, -156.10116949],
 [ 150.23207937,  301.31376595],
 [  91.00920901, -391.283763  ],
 [ 202.89662724, -269.38043241],
 [ 361.66623976, -106.96493868],
 [-219.40612786, -244.06020508]]) 

>>> result.funl
array([-959.64066272, -718.16745962, -704.80659592, -565.99778097,
 -559.78685655, -557.36868733, -507.87385942, -493.9605115 ,
 -426.48799655, -421.15571437, -419.31194957, -410.98477763]) 

这些结果在应用中非常有用，特别是在需要许多全局极小值和其他全局极小值值的情况下，或者在局部极小值可以为系统提供洞察力的情况下（例如物理化学中的形态学[4]）。

如果我们想要找到更多的局部极小值，我们可以增加采样点或迭代次数的数量。我们将增加采样点数到 64，并将迭代次数从默认值 1 增加到 3。使用simplicial，这将为我们提供 64 x 3 = 192 个初始采样点。

>>> result_2 = shgo(eggholder,
...                 bounds, n=64, iters=3, sampling_method='sobol')
>>> len(result.xl), len(result_2.xl)
(12, 23) 

注意，例如n=192, iters=1和n=64, iters=3之间的差异。在第一种情况下，仅一次处理最小化池中的有前途点。在后一种情况下，它每 64 个采样点处理一次，总共 3 次。

要演示解决具有非线性约束的问题，请考虑 Hock 和 Schittkowski 问题 73（牛饲料）的以下示例[3]：

minimize: f = 24.55 * x_1 + 26.75 * x_2 + 39 * x_3 + 40.50 * x_4

subject to: 2.3 * x_1 + 5.6 * x_2 + 11.1 * x_3 + 1.3 * x_4 - 5    >= 0,

            12 * x_1 + 11.9 * x_2 + 41.8 * x_3 + 52.1 * x_4 - 21
                -1.645 * sqrt(0.28 * x_1**2 + 0.19 * x_2**2 +
                              20.5 * x_3**2 + 0.62 * x_4**2)      >= 0,

            x_1 + x_2 + x_3 + x_4 - 1                             == 0,

            1 >= x_i >= 0 for all i 

在[3]中给出的近似答案是：

f([0.6355216, -0.12e-11, 0.3127019, 0.05177655]) = 29.894378 

>>> def f(x):  # (cattle-feed)
...     return 24.55*x[0] + 26.75*x[1] + 39*x[2] + 40.50*x[3]
...
>>> def g1(x):
...     return 2.3*x[0] + 5.6*x[1] + 11.1*x[2] + 1.3*x[3] - 5  # >=0
...
>>> def g2(x):
...     return (12*x[0] + 11.9*x[1] +41.8*x[2] + 52.1*x[3] - 21
...             - 1.645 * np.sqrt(0.28*x[0]**2 + 0.19*x[1]**2
...                             + 20.5*x[2]**2 + 0.62*x[3]**2)
...             ) # >=0
...
>>> def h1(x):
...     return x[0] + x[1] + x[2] + x[3] - 1  # == 0
...
>>> cons = ({'type': 'ineq', 'fun': g1},
...         {'type': 'ineq', 'fun': g2},
...         {'type': 'eq', 'fun': h1})
>>> bounds = [(0, 1.0),]*4
>>> res = shgo(f, bounds, n=150, constraints=cons)
>>> res
 message: Optimization terminated successfully.
 success: True
 fun: 29.894378159142136
 funl: [ 2.989e+01]
 x: [ 6.355e-01  1.137e-13  3.127e-01  5.178e-02] # may vary
 xl: [[ 6.355e-01  1.137e-13  3.127e-01  5.178e-02]] # may vary
 nit: 1
 nfev: 142 # may vary
 nlfev: 35 # may vary
 nljev: 5
 nlhev: 0 

>>> g1(res.x), g2(res.x), h1(res.x)
(-5.062616992290714e-14, -2.9594104944408173e-12, 0.0) 

scipy.optimize.dual_annealing

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.dual_annealing.html#scipy.optimize.dual_annealing

scipy.optimize.dual_annealing(func, bounds, args=(), maxiter=1000, minimizer_kwargs=None, initial_temp=5230.0, restart_temp_ratio=2e-05, visit=2.62, accept=-5.0, maxfun=10000000.0, seed=None, no_local_search=False, callback=None, x0=None)

使用双重退火法找到函数的全局最小值。

参数：

func可调用对象

要最小化的目标函数。必须以f(x, *args)的形式给出，其中x是一维数组形式的参数，args是一个包含完全指定函数所需的任何额外固定参数的元组。

边界序列或Bounds类

变量的边界。有两种指定边界的方式：

1. Bounds类的实例。

2. 对于x中的每个元素，都有(min, max)对的序列。

args元组, 可选

任何完全指定目标函数所需的额外固定参数。

最大迭代次数int, 可选

全局搜索迭代的最大次数。默认值为 1000。

minimizer_kwargs字典, 可选

传递给局部最小化器(minimize)的额外关键字参数。一些重要的选项可能包括：method用于指定最小化方法和args用于目标函数的额外参数。

初始温度float, 可选

初始温度，使用较高的值可以促进更广泛的能量景观搜索，允许dual_annealing逃离被困在其中的局部极小值。默认值为 5230。范围为(0.01, 5.e4]。

重启温度比率float, 可选

在退火过程中，温度逐渐降低，当达到initial_temp * restart_temp_ratio时，会触发重新退火过程。比率的默认值为 2e-5。范围为(0, 1)。

访问率float, 可选

访问分布参数。默认值为 2.62。较高的值使访问分布尾部更重，这使得算法跳到更远的区域。值的范围为(1, 3]。

接受率float, 可选

接受分布参数。用于控制接受概率。接受参数越低，接受概率越小。默认值为-5.0，范围为(-1e4, -5]。

最大函数调用次数int, 可选

目标函数调用的软限制。如果算法在局部搜索中间，超出这个数值后，算法将在局部搜索完成后停止。默认值为 1e7。

种子{None, int, numpy.random.Generator, numpy.random.RandomState}, 可选

如果 seed 为 None（或 np.random），则使用 numpy.random.RandomState 单例。如果 seed 是一个整数，则使用一个新的 RandomState 实例，并用 seed 初始化。如果 seed 已经是 Generator 或 RandomState 实例，则使用该实例。指定 seed 可重复进行最小化。使用此种子生成的随机数仅影响访问分布函数和新坐标生成。

no_local_searchbool, optional

如果将 no_local_search 设置为 True，则将执行传统的广义模拟退火，不会应用局部搜索策略。

callbackcallable, optional

带有签名 callback(x, f, context) 的回调函数，将对找到的所有最小值进行调用。x 和 f 是最新最小值的坐标和函数值，context 的值在 [0, 1, 2] 范围内，具有以下含义：

• 0：在退火过程中检测到最小值。
• 1：在局部搜索过程中发生检测。
• 2：在双退火过程中完成检测。

如果回调实现返回 True，则算法将停止。

x0ndarray, shape(n,), optional

单个 N-D 起始点的坐标。

返回：

resOptimizeResult

优化结果表示为 OptimizeResult 对象。重要属性包括：x 解数组，fun 在解处的函数值，以及 message 描述终止原因。查看 OptimizeResult 以了解其他属性的描述。

注：

这个函数实现了双退火优化。这种随机方法源于[3]，结合了 CSA（经典模拟退火）和 FSA（快速模拟退火）[1] [2]，并采用一种策略，在接受的位置上应用局部搜索[4]。这种算法的另一种实现在[5]中有描述，并在[6]中进行了基准测试。这种方法引入了一种高级方法来优化广义退火过程中找到的解。该算法使用扭曲的柯西-洛伦兹访问分布，其形状由参数 (q_{v}) 控制。

[g_{q_{v}}(\Delta x(t)) \propto \frac{ \ \left[T_{q_{v}}(t) \right]^{-\frac{D}{3-q_{v}}}}{ \ \left[{1+(q_{v}-1)\frac{(\Delta x(t))^{2}} { \ \left[T_{q_{v}}(t)\right]^{{\frac{2}{3-q_{v}}}}}\right]}{ \ \frac{1}{q_{v}-1}+\frac{D-1}{2}}}]

其中 (t) 是人造时间。这种访问分布用于生成变量 (x(t)) 的试验跳跃距离 (\Delta x(t))，在人造温度 (T_{q_{v}}(t)) 下。

从起始点开始，调用访问分布函数后，接受概率计算如下：

[p_{q_{a}} = \min{{1,\left[1-(1-q_{a}) \beta \Delta E \right]^{ \ \frac{1}{1-q_{a}}}}}]

其中 (q_{a}) 是接受参数。对于 (q_{a}<1)，在 (1-(1-q_{a}) \beta \Delta E < 0) 的情况下，将分配零接受概率。

[[1-(1-q_{a}) \beta \Delta E] < 0]

人工温度 (T_{q_{v}}(t)) 根据以下方式递减：

[T_{q_{v}}(t) = T_{q_{v}}(1) \frac{2^{q_{v}-1}-1}{\left( \ 1 + t\right)^{q_{v}-1}-1}]

其中 (q_{v}) 是访问参数。

版本 1.2.0 的新功能。

参考文献

[1]

Tsallis C. 可能是 Boltzmann-Gibbs 统计的一般化。《统计物理学杂志》，52, 479-487 (1998)。

[2]

Tsallis C, Stariolo DA. 广义模拟退火。《物理学 A》，233, 395-406 (1996)。

[3]

Xiang Y, Sun DY, Fan W, Gong XG. 广义模拟退火算法及其在汤姆森模型中的应用。《物理学快报 A》，233, 216-220 (1997)。DOI:10.18637/jss.v060.i06

[4]

Xiang Y, Gong XG. 广义模拟退火算法的效率。《物理评论 E》，62, 4473 (2000)。

[5]

Xiang Y, Gubian S, Suomela B, Hoeng J. 用于高效全局优化的广义模拟退火：R 包 GenSA。《R 语言杂志》，Volume 5/1 (2013)。

[6]

Mullen, K. R 中的连续全局优化。《统计软件杂志》，60(6), 1 - 45, (2014)。DOI:10.18637/jss.v060.i06

示例

下面的例子是一个 10 维问题，有许多局部极小值。涉及的函数称为 Rastrigin (en.wikipedia.org/wiki/Rastrigin_function)

>>> import numpy as np
>>> from scipy.optimize import dual_annealing
>>> func = lambda x: np.sum(x*x - 10*np.cos(2*np.pi*x)) + 10*np.size(x)
>>> lw = [-5.12] * 10
>>> up = [5.12] * 10
>>> ret = dual_annealing(func, bounds=list(zip(lw, up)))
>>> ret.x
array([-4.26437714e-09, -3.91699361e-09, -1.86149218e-09, -3.97165720e-09,
 -6.29151648e-09, -6.53145322e-09, -3.93616815e-09, -6.55623025e-09,
 -6.05775280e-09, -5.00668935e-09]) # random
>>> ret.fun
0.000000 

scipy.optimize.direct

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.direct.html#scipy.optimize.direct

scipy.optimize.direct(func, bounds, *, args=(), eps=0.0001, maxfun=None, maxiter=1000, locally_biased=True, f_min=-inf, f_min_rtol=0.0001, vol_tol=1e-16, len_tol=1e-06, callback=None)

使用 DIRECT 算法找到函数的全局最小值。

参数：

funccallable

要最小化的目标函数。func(x, *args) -> float，其中x是形状为(n,)的一维数组，args是完全指定函数所需的固定参数的元组。

bounds序列或Bounds

变量的界限。有两种指定界限的方式：

1. Bounds类的实例。

2. 对于x中的每个元素，(min, max)对。

argstuple，可选

完全指定目标函数所需的任何额外固定参数。

epsfloat，可选

当前最佳超矩形与下一个可能的最优超矩形之间的目标函数值的最小必需差异。因此，eps用作局部和全局搜索之间的折衷：它越小，搜索就越局部。默认为 1e-4。

maxfunint 或 None，可选

目标函数评估的大致上限。如果为None，则自动设置为1000 * N，其中N表示维度的数量。如有必要，将对 DIRECT 的 RAM 使用进行限制，以保持约为 1GiB。这仅适用于维度非常高和max_fun过大的问题。默认为None。

maxiterint，可选

最大迭代次数。默认为 1000。

locally_biasedbool，可选

如果为True（默认值），则使用称为 DIRECT_L 的算法的局部偏置变体。如果为False，则使用原始的无偏 DIRECT 算法。对于具有许多局部最小值的困难问题，建议使用False。

f_minfloat，可选

全局最优解的函数值。仅在已知全局最优解时设置此值。默认为-np.inf，因此此终止准则被禁用。

f_min_rtolfloat，可选

当当前最佳最小值f和提供的全局最小值f_min之间的相对误差小于f_min_rtol时，终止优化。如果f_min也设置了，则使用此参数。必须介于 0 和 1 之间。默认为 1e-4。

vol_tolfloat，可选

当包含最低函数值的超矩形的体积小于完整搜索空间的vol_tol时，终止优化。必须介于 0 和 1 之间。默认为 1e-16。

len_tolfloat，可选

如果 locally_biased=True，则当包含最低函数值的超矩形的归一化最大边长的一半小于 len_tol 时终止优化。如果 locally_biased=False，则当包含最低函数值的超矩形的归一化对角线的一半小于 len_tol 时终止优化。必须介于 0 和 1 之间。默认值为 1e-6。

callback 可调用对象，可选

具有签名 callback(xk) 的回调函数，其中 xk 表示迄今为止找到的最佳函数值。

返回：

res OptimizeResult

表示优化结果的 OptimizeResult 对象。重要属性包括：x 解数组，success 布尔标志，指示优化器是否成功退出，以及 message 描述终止原因。详见 OptimizeResult 获取其他属性的描述。

笔记

DIviding RECTangles (DIRECT) 是一种确定性全局优化算法，能够通过在搜索空间中采样潜在解来最小化黑盒函数，其中变量受下限和上限约束 [1]。该算法首先将搜索空间标准化为 n 维单位超立方体。它在这个超立方体的中心点和每个坐标方向上的 2n 个点处采样函数。使用这些函数值，DIRECT 将域划分为超矩形，每个超矩形的中心点恰好是一个采样点。在每次迭代中，DIRECT 使用默认为 1e-4 的eps参数选择一些现有超矩形进行进一步划分。这个划分过程持续进行，直到达到最大迭代次数或允许的最大函数评估次数，或者包含到目前为止找到的最小值的超矩形足够小。如果指定了f_min，优化将在相对容差内达到这个函数值时停止。默认情况下使用 DIRECT 的局部偏向变体（最初称为 DIRECT_L） [2]。它使搜索更加局部偏向，并且对只有少数局部最小值的情况更有效。

关于终止标准的说明：vol_tol 是指包含到目前为止找到的最低函数值的超矩形的体积。这个体积随问题维数的增加呈指数下降。因此，为了避免在更高维问题上过早终止算法，应减小 vol_tol。但对于 len_tol 不适用此规则：它指的是最大边长的一半（对于 locally_biased=True）或者超矩形对角线的一半（对于 locally_biased=False）。

这段代码基于 Gablonsky 等人的 DIRECT 2.0.4 Fortran 代码，可以在ctk.math.ncsu.edu/SOFTWARE/DIRECTv204.tar.gz找到。这个原始版本最初通过 f2c 转换，然后由 Steven G. Johnson 在 2007 年 8 月为 NLopt 项目进行了清理和重新组织。direct函数封装了 C 实现。

新功能版本 1.9.0 中的更新。

参考文献

[1]

Jones, D.R., Perttunen, C.D. & Stuckman, B.E. 没有 Lipschitz 常数的 Lipschitz 优化。《优化理论与应用期刊》79, 157-181 (1993).

[2]

Gablonsky, J., Kelley, C. DIRECT 算法的一种本地偏向形式。《全局优化期刊》21, 27-37 (2001).

示例

以下示例是一个二维问题，有四个局部最小值：最小化 Styblinski-Tang 函数（en.wikipedia.org/wiki/Test_functions_for_optimization）。

>>> from scipy.optimize import direct, Bounds
>>> def styblinski_tang(pos):
...     x, y = pos
...     return 0.5 * (x**4 - 16*x**2 + 5*x + y**4 - 16*y**2 + 5*y)
>>> bounds = Bounds([-4., -4.], [4., 4.])
>>> result = direct(styblinski_tang, bounds)
>>> result.x, result.fun, result.nfev
array([-2.90321597, -2.90321597]), -78.3323279095383, 2011 

找到了正确的全局最小值，但使用了大量的函数评估（2011）。可以通过放宽终止容差vol_tol和len_tol来提前停止 DIRECT。

>>> result = direct(styblinski_tang, bounds, len_tol=1e-3)
>>> result.x, result.fun, result.nfev
array([-2.9044353, -2.9044353]), -78.33230330754142, 207 

scipy.optimize.least_squares

原文链接：docs.scipy.org/doc/scipy-1.12.0/reference/generated/scipy.optimize.least_squares.html#scipy.optimize.least_squares

scipy.optimize.least_squares(fun, x0, jac='2-point', bounds=(-inf, inf), method='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=1.0, loss='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options={}, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs={})

解决带有变量边界的非线性最小二乘问题。

给定残差 f(x)（一个 m-D 实函数的 n 个实变量）和损失函数 rho(s)（一个标量函数），least_squares找到成本函数 F(x)的局部最小值：

minimize F(x) = 0.5 * sum(rho(f_i(x)**2), i = 0, ..., m - 1)
subject to lb <= x <= ub 

损失函数 rho(s)的目的是减少离群值对解决方案的影响。

参数：

fun可调用

计算残差向量的函数，具有签名fun(x, *args, **kwargs)，即最小化将相对于其第一个参数进行。传递给此函数的参数x是形状为(n,)的 ndarray（即使对于 n=1，也不是标量）。它必须分配并返回形状为(m,)的 1-D 数组或标量。如果参数x是复数或函数fun返回复数残差，则必须将其包装在实数参数的实函数中，如示例部分的最后所示。

x0array_like，形状为(n,)或 float

独立变量的初始猜测。如果是 float，它将被视为具有一个元素的 1-D 数组。当method为‘trf’时，初始猜测可能会被略微调整，以确保足够位于给定的bounds内。

jac{‘2-point’, ‘3-point’, ‘cs’, callable}，可选

计算雅可比矩阵的方法（一个 m×n 矩阵，其中元素(i, j)是 f[i]关于 x[j]的偏导数）。关键字选择了用于数值估计的有限差分方案。方案“3-point”更精确，但需要两倍的操作量比“2-point”（默认）多。方案“cs”使用复步长，虽然可能是最精确的，但仅当fun正确处理复数输入并且能在复平面上解析延续时适用。方法“lm”始终使用“2-point”方案。如果可调用，则用作jac(x, *args, **kwargs)，应返回雅可比矩阵的良好近似值（或确切值），作为数组（np.atleast_2d 应用），稀疏矩阵（出于性能考虑，优先使用 csr_matrix）或scipy.sparse.linalg.LinearOperator。

bounds形如 2 元组的 array_like 或Bounds，可选

有两种指定边界的方法：

1. Bounds类的实例
3. 独立变量的上下界。默认无界。每个数组必须与x0的大小相匹配或者是标量，在后一种情况下，所有变量的边界将相同。使用适当符号的np.inf以禁用所有或部分变量的边界。

method{‘trf’, ‘dogbox’, ‘lm’}, optional

执行最小化的算法。

• ‘trf’：反射信赖区域算法，特别适用于具有边界的大型稀疏问题。通常是健壮的方法。
• ‘dogbox’：矩形信赖区域的狗腿算法，典型应用场景是具有边界的小问题。不推荐处理秩亏的雅可比矩阵问题。
• ‘lm’：MINPACK 中实现的 Levenberg-Marquardt 算法。不处理边界和稀疏雅可比矩阵。通常是小型无约束问题的最有效方法。

默认为‘trf’。更多信息请参见注释。

ftolfloat 或 None，可选

终止由成本函数变化的公差。默认为 1e-8。当dF < ftol * F且在上一步中局部二次模型与真实模型之间有足够协议时，优化过程停止。

若为 None 且‘method’不为‘lm’，则此条件下的终止被禁用。若‘method’为‘lm’，则此公差必须高于机器 epsilon。

xtolfloat 或 None，可选

终止由独立变量变化的公差。默认为 1e-8。确切条件取决于所使用的method：

• 对于‘trf’和‘dogbox’：norm(dx) < xtol * (xtol + norm(x))。
• 对于‘lm’：Delta < xtol * norm(xs)，其中Delta是信赖区域半径，xs是根据x_scale参数缩放后的x的值（见下文）。

若为 None 且‘method’不为‘lm’，则此条件下的终止被禁用。若‘method’为‘lm’，则此公差必须高于机器 epsilon。

gtolfloat 或 None，可选

终止由梯度范数的公差。默认为 1e-8。确切条件取决于所使用的method：

• 对于‘trf’：norm(g_scaled, ord=np.inf) < gtol，其中g_scaled是考虑边界存在的梯度值[STIR]。
• 对于‘dogbox’：norm(g_free, ord=np.inf) < gtol，其中g_free是相对于在边界上不处于最佳状态的变量的梯度。
• 对于‘lm’：雅可比矩阵的列与残差向量之间夹角的最大绝对值小于gtol，或者残差向量为零。

若为 None 且‘method’不为‘lm’，则此条件下的终止被禁用。若‘method’为‘lm’，则此公差必须高于机器 epsilon。

x_scalearray_like 或‘jac’，可选

每个变量的特征尺度。设置 x_scale 相当于在缩放变量 xs = x / x_scale 中重新表述问题。另一种观点是，沿第 j 维的信任区域大小与 x_scale[j] 成比例。通过设置 x_scale，可以实现改进的收敛性，使得沿着任何缩放变量的给定大小步骤对成本函数产生类似的影响。如果设置为 ‘jac’，则使用雅可比矩阵列的逆范数进行迭代更新尺度（如 [JJMore] 中描述）。

lossstr 或 callable，可选

确定损失函数。允许以下关键字值：

• ‘linear’（默认）：rho(z) = z。给出一个标准的最小二乘问题。
• ‘soft_l1’：rho(z) = 2 * ((1 + z)**0.5 - 1)。l1（绝对值）损失的平滑逼近。通常是鲁棒最小二乘的良好选择。
• ‘huber’ : rho(z) = z if z <= 1 else 2*z**0.5 - 1。与 ‘soft_l1’ 类似工作。
• ‘cauchy’ : rho(z) = ln(1 + z). 严重削弱离群值的影响，但可能会导致优化过程中的困难。
• ‘arctan’：rho(z) = arctan(z)。限制单个残差的最大损失，具有类似 ‘cauchy’ 的特性。

如果可调用，它必须接受一个一维 ndarray z=f**2 并返回一个形状为 (3, m) 的 array_like，其中第 0 行包含函数值，第 1 行包含一阶导数，第 2 行包含二阶导数。方法 ‘lm’ 仅支持 ‘linear’ 损失。

f_scalefloat，可选

变量之间的软边界值，默认为 1.0。损失函数的评估如下 rho_(f**2) = C**2 * rho(f**2 / C**2)，其中 C 是 f_scale，而 rho 受 loss 参数控制。对于 loss='linear'，此参数没有影响，但对于其他 loss 值，它至关重要。

max_nfevNone 或 int，可选

函数评估的最大次数在终止之前。如果为 None（默认），则自动选择该值：

• 对于 ‘trf’ 和 ‘dogbox’：100 * n。
• For ‘lm’ : 100 * n if jac is callable and 100 * n * (n + 1) otherwise (because ‘lm’ counts function calls in Jacobian estimation).

diff_stepNone 或 array_like，可选

确定雅可比矩阵有限差分近似的相对步长。实际步长计算为 x * diff_step。如果为 None（默认），则 diff_step 被认为是用于有限差分方案的常规“最优”机器 epsilon 的幂 [NR]。

tr_solver{None, ‘exact’, ‘lsmr’}，可选

解决信任区域子问题的方法，仅对 ‘trf’ 和 ‘dogbox’ 方法有效。

• ‘exact’ 适用于问题规模不是很大且雅可比矩阵稠密的情况。每次迭代的计算复杂度与雅可比矩阵的奇异值分解相当。
• ‘lsmr’适用于具有稀疏和大雅可比矩阵的问题。它使用迭代过程scipy.sparse.linalg.lsmr来找到线性最小二乘问题的解，并且只需矩阵-向量乘积评估。

如果为 None（默认值），则求解器基于第一次迭代返回的雅可比矩阵类型选择。

tr_options字典，可选

关键字选项传递给信任区域求解器。

• tr_solver='exact'：tr_options将被忽略。
• tr_solver='lsmr'：scipy.sparse.linalg.lsmr的选项。此外，method='trf'支持‘regularize’选项（布尔值，默认为 True），该选项在正规方程中添加正则化项，如果雅可比矩阵是秩缺乏的[Byrd]（eq. 3.4）时可以改善收敛性。

jac_sparsity{None, array_like, 稀疏矩阵}，可选

定义雅可比矩阵的稀疏结构用于有限差分估计，其形状必须为(m, n)。如果雅可比矩阵每行只有少量非零元素，则提供稀疏结构将极大加速计算[Curtis]。零条目意味着雅可比矩阵中对应元素恒为零。如果提供，则强制使用‘lsmr’信任区域求解器。如果为 None（默认值），则将使用密集差分。对‘lm’方法无效。

详细{0, 1, 2}，可选

算法详细程度：

• 0（默认值）：静默工作。
• 1：显示终止报告。
• 2：在迭代过程中显示进展（不支持‘lm’方法）。

args, kwargs元组和字典，可选

传递给fun和jac的额外参数。默认情况下两者为空。调用签名为fun(x, *args, **kwargs)，jac相同。

返回：

resultOptimizeResult

OptimizeResult，定义了以下字段：

xndarray，形状为(n,)

找到解决方案。

costfloat

解处成本函数的值。

funndarray，形状为(m,)

解处的残差向量。

jacndarray、稀疏矩阵或线性算子，形状为(m, n)

在解处的修改雅可比矩阵，即 J^T J 是成本函数海森矩阵的高斯-牛顿近似。类型与算法使用的类型相同。

gradndarray，形状为(m,)

解处成本函数的梯度。

优越性浮点数

一阶最优性度量。在无约束问题中，它总是梯度的一致范数。在有约束问题中，它是在迭代过程中与gtol比较的量。

active_maskndarray 整数，形状为(n,)

每个分量显示相应约束是否活跃（即变量是否位于边界处）：

• 0：约束未生效。
• -1：下界生效。
• 1 : 上限激活。

对于 ‘trf’ 方法来说可能有些随意，因为它生成严格可行迭代序列，并且 active_mask 在容差阈值内确定。

nfevint

函数评估次数。‘trf’ 和 ‘dogbox’ 方法不计算数值雅可比逼近的函数调用次数，而‘lm’方法则计算。

njevint 或 None

雅可比矩阵评估次数。如果在 ‘lm’ 方法中使用数值雅可比逼近，则设置为 None。

statusint

算法终止的原因：

• -1 : 从 MINPACK 返回的不合适的输入参数状态。
• 0 : 超过了最大函数评估次数。
• 1 : gtol 终止条件满足。
• 2 : ftol 终止条件满足。
• 3 : xtol 终止条件满足。
• 4 : ftol 和 xtol 终止条件均满足。

messagestr

终止原因的口头描述。

successbool

如果满足其中一个收敛条件，则返回 True（status > 0）。

另见

leastsq

MINPACK 实现的 Levenberg-Marquadt 算法的遗留包装器。

curve_fit

用于曲线拟合问题的最小二乘最小化。

注释

‘lm’ 方法（Levenberg-Marquardt）调用 MINPACK 中实现的最小二乘算法的包装器（lmder, lmdif）。它以信任区域类型算法的形式运行 Levenberg-Marquardt 算法。该实现基于文献 [JJMore]，非常稳健和高效，采用了许多巧妙的技巧。对于无约束问题，它应该是你的首选。注意它不支持边界条件，且在 m < n 时不起作用。

方法‘trf’（Trust Region Reflective）的动机源于解决方程组的过程，这组成了形式化为[STIR]中约束边界最小化问题的一阶最优性条件。该算法通过迭代解决增强的信赖域子问题，其特殊对角二次项增强了与边界的距离和梯度方向决定的信赖域形状。这些增强有助于避免直接朝着边界步进，并有效地探索变量空间的整体。为了进一步提高收敛速度，该算法考虑了从边界反射的搜索方向。为了符合理论要求，算法保持迭代点始终可行。对于稠密雅可比矩阵，信赖域子问题通过一种与[JJMore]描述的方法非常相似的准确方法来解决（在 MINPACK 中实现）。与 MINPACK 实现的不同之处在于，雅可比矩阵的奇异值分解在每次迭代中只进行一次，而不是 QR 分解和一系列 Givens 旋转消元。对于大型稀疏雅可比矩阵，使用二维子空间方法解决信赖域子问题，该子空间由梯度的缩放和scipy.sparse.linalg.lsmr提供的近似 Gauss-Newton 解决方案所构成[STIR]，[Byrd]。当不加约束时，该算法与 MINPACK 非常相似，并且通常具有可比较的性能。该算法在无界和有界问题中表现相当强大，因此被选择为默认算法。

方法‘dogbox’在信赖域框架中运作，但考虑到矩形信赖域，而不是传统的椭球体[Voglis]。当前信赖域与初始边界的交集再次是矩形，因此在每次迭代中，通过 Powell 的 dogleg 方法近似地解决了一个受限二次最小化问题[NumOpt]。对于稠密雅可比矩阵，可以通过准确计算 Gauss-Newton 步骤，或者对于大型稀疏雅可比矩阵，可以通过scipy.sparse.linalg.lsmr进行近似计算。当雅可比矩阵的秩小于变量数时，该算法可能展现出较慢的收敛速度。在变量数较少的有界问题中，该算法通常优于‘trf’。

鲁棒损失函数的实现如 [BA] 描述的那样。其思想是在每次迭代中修改残差向量和雅可比矩阵，使得计算的梯度和 Gauss-Newton Hessian 近似与成本函数的真实梯度和 Hessian 近似匹配。然后算法按正常方式继续，即，鲁棒损失函数被实现为标准最小二乘算法的简单包装。

新版本 0.17.0 中的新增内容。

参考文献

[STIR] (1,2,3)

M. A. Branch, T. F. Coleman 和 Y. Li，《A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems》，《SIAM Journal on Scientific Computing》，第 21 卷，第 1 期，pp. 1-23，1999。

[牛顿拉夫逊法]

William H. Press 等人，《Numerical Recipes. The Art of Scientific Computing. 3rd edition》，第 5.7 节。

[Byrd] (1,2)

R. H. Byrd, R. B. Schnabel 和 G. A. Shultz，《Approximate solution of the trust region problem by minimization over two-dimensional subspaces》，《Math. Programming》，第 40 卷，pp. 247-263，1988。

[Curtis]

A. Curtis, M. J. D. Powell 和 J. Reid，《On the estimation of sparse Jacobian matrices》，《Journal of the Institute of Mathematics and its Applications》，第 13 卷，pp. 117-120，1974。

[JJMore] (1,2,3)

J. J. More，《The Levenberg-Marquardt Algorithm: Implementation and Theory》，《Numerical Analysis》，编者 G. A. Watson，Lecture Notes in Mathematics 630，Springer Verlag，pp. 105-116，1977。

[Voglis]

C. Voglis 和 I. E. Lagaris，《A Rectangular Trust Region Dogleg Approach for Unconstrained and Bound Constrained Nonlinear Optimization》，WSEAS International Conference on Applied Mathematics，希腊科尔富，2004。

[数值优化]

J. Nocedal 和 S. J. Wright，《Numerical optimization, 2nd edition》，第四章。

[BA]

B. Triggs 等人，《Bundle Adjustment - A Modern Synthesis》，《Proceedings of the International Workshop on Vision Algorithms: Theory and Practice》，pp. 298-372，1999。

示例

在这个例子中，我们在独立变量上找到了 Rosenbrock 函数的最小值，没有约束。

>>> import numpy as np
>>> def fun_rosenbrock(x):
...     return np.array([10 * (x[1] - x[0]**2), (1 - x[0])]) 

注意，我们只提供残差向量。算法将成本函数构建为残差平方和，这给出了 Rosenbrock 函数。精确的最小值在 x = [1.0, 1.0] 处。

>>> from scipy.optimize import least_squares
>>> x0_rosenbrock = np.array([2, 2])
>>> res_1 = least_squares(fun_rosenbrock, x0_rosenbrock)
>>> res_1.x
array([ 1.,  1.])
>>> res_1.cost
9.8669242910846867e-30
>>> res_1.optimality
8.8928864934219529e-14 

现在我们限制变量，使得先前的解决方案变得不可行。具体来说，我们要求 x[1] >= 1.5，而 x[0] 保持未约束。为此，我们在 least_squares 中的 bounds 参数中指定了形式为 bounds=([-np.inf, 1.5], np.inf)。

我们还提供了分析雅可比矩阵：

>>> def jac_rosenbrock(x):
...     return np.array([
...         [-20 * x[0], 10],
...         [-1, 0]]) 

将所有这些放在一起，我们看到新解决方案位于边界上：

>>> res_2 = least_squares(fun_rosenbrock, x0_rosenbrock, jac_rosenbrock,
...                       bounds=([-np.inf, 1.5], np.inf))
>>> res_2.x
array([ 1.22437075,  1.5       ])
>>> res_2.cost
0.025213093946805685
>>> res_2.optimality
1.5885401433157753e-07 

现在我们解一个方程组（即，成本函数在最小值处应为零），对一个有 100000 个变量的 Broyden 三对角向量值函数进行约束：

>>> def fun_broyden(x):
...     f = (3 - x) * x + 1
...     f[1:] -= x[:-1]
...     f[:-1] -= 2 * x[1:]
...     return f 

相应的雅可比矩阵是稀疏的。我们告诉算法通过有限差分来估计它，并提供雅可比矩阵的稀疏结构，以显著加快这个过程。

>>> from scipy.sparse import lil_matrix
>>> def sparsity_broyden(n):
...     sparsity = lil_matrix((n, n), dtype=int)
...     i = np.arange(n)
...     sparsity[i, i] = 1
...     i = np.arange(1, n)
...     sparsity[i, i - 1] = 1
...     i = np.arange(n - 1)
...     sparsity[i, i + 1] = 1
...     return sparsity
...
>>> n = 100000
>>> x0_broyden = -np.ones(n)
...
>>> res_3 = least_squares(fun_broyden, x0_broyden,
...                       jac_sparsity=sparsity_broyden(n))
>>> res_3.cost
4.5687069299604613e-23
>>> res_3.optimality
1.1650454296851518e-11 

让我们还用鲁棒损失函数解决一个曲线拟合问题，以处理数据中的离群值。定义模型函数为y = a + b * exp(c * t)，其中 t 是预测变量，y 是观测值，a、b、c 是要估计的参数。

首先，定义生成带有噪声和离群值数据的函数，定义模型参数，并生成数据：

>>> from numpy.random import default_rng
>>> rng = default_rng()
>>> def gen_data(t, a, b, c, noise=0., n_outliers=0, seed=None):
...     rng = default_rng(seed)
...
...     y = a + b * np.exp(t * c)
...
...     error = noise * rng.standard_normal(t.size)
...     outliers = rng.integers(0, t.size, n_outliers)
...     error[outliers] *= 10
...
...     return y + error
...
>>> a = 0.5
>>> b = 2.0
>>> c = -1
>>> t_min = 0
>>> t_max = 10
>>> n_points = 15
...
>>> t_train = np.linspace(t_min, t_max, n_points)
>>> y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3) 

定义计算残差和参数初始估计的函数。

>>> def fun(x, t, y):
...     return x[0] + x[1] * np.exp(x[2] * t) - y
...
>>> x0 = np.array([1.0, 1.0, 0.0]) 

计算标准最小二乘解：

>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train)) 

现在使用两个不同的鲁棒损失函数计算两个解。参数f_scale设为 0.1，意味着内点残差不应显著超过 0.1（所用的噪声水平）。

>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1,
...                             args=(t_train, y_train))
>>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1,
...                         args=(t_train, y_train)) 

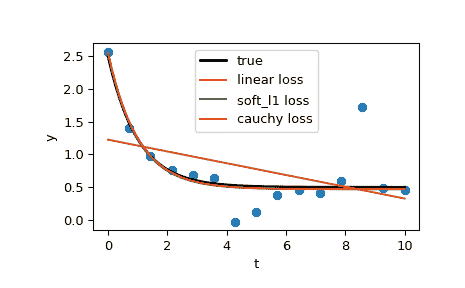
最后，绘制所有曲线。我们可以看到通过选择适当的loss，即使在存在强离群值的情况下，我们也可以得到接近最优的估计。但请记住，通常建议首先尝试使用‘soft_l1’或‘huber’损失（如有必要），因为其他两个选项可能会在优化过程中造成困难。

>>> t_test = np.linspace(t_min, t_max, n_points * 10)
>>> y_true = gen_data(t_test, a, b, c)
>>> y_lsq = gen_data(t_test, *res_lsq.x)
>>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x)
>>> y_log = gen_data(t_test, *res_log.x)
...
>>> import matplotlib.pyplot as plt
>>> plt.plot(t_train, y_train, 'o')
>>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true')
>>> plt.plot(t_test, y_lsq, label='linear loss')
>>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss')
>>> plt.plot(t_test, y_log, label='cauchy loss')
>>> plt.xlabel("t")
>>> plt.ylabel("y")
>>> plt.legend()
>>> plt.show() 

在下一个示例中，我们展示了如何使用least_squares()来优化复变量的复值残差函数。考虑以下函数：

>>> def f(z):
...     return z - (0.5 + 0.5j) 

我们将其封装为一个处理实部和虚部作为独立变量的实变量函数，返回实残差：

>>> def f_wrap(x):
...     fx = f(x[0] + 1j*x[1])
...     return np.array([fx.real, fx.imag]) 

因此，我们不再优化原始的 n 个复变量的 m-D 复杂函数，而是优化一个 2n 个实变量的 2m-D 实函数：

>>> from scipy.optimize import least_squares
>>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1]))
>>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j
>>> z
(0.49999999999925893+0.49999999999925893j) 

n = np.linspace(t_min, t_max, n_points)

y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3)

定义计算残差和参数初始估计的函数。

```py
>>> def fun(x, t, y):
...     return x[0] + x[1] * np.exp(x[2] * t) - y
...
>>> x0 = np.array([1.0, 1.0, 0.0]) 

计算标准最小二乘解：

>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train)) 

现在使用两个不同的鲁棒损失函数计算两个解。参数f_scale设为 0.1，意味着内点残差不应显著超过 0.1（所用的噪声水平）。

>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1,
...                             args=(t_train, y_train))
>>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1,
...                         args=(t_train, y_train)) 

最后，绘制所有曲线。我们可以看到通过选择适当的loss，即使在存在强离群值的情况下，我们也可以得到接近最优的估计。但请记住，通常建议首先尝试使用‘soft_l1’或‘huber’损失（如有必要），因为其他两个选项可能会在优化过程中造成困难。

>>> t_test = np.linspace(t_min, t_max, n_points * 10)
>>> y_true = gen_data(t_test, a, b, c)
>>> y_lsq = gen_data(t_test, *res_lsq.x)
>>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x)
>>> y_log = gen_data(t_test, *res_log.x)
...
>>> import matplotlib.pyplot as plt
>>> plt.plot(t_train, y_train, 'o')
>>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true')
>>> plt.plot(t_test, y_lsq, label='linear loss')
>>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss')
>>> plt.plot(t_test, y_log, label='cauchy loss')
>>> plt.xlabel("t")
>>> plt.ylabel("y")
>>> plt.legend()
>>> plt.show() 

[外链图片转存中…(img-GOoOyzkR-1719632445202)]

在下一个示例中，我们展示了如何使用least_squares()来优化复变量的复值残差函数。考虑以下函数：

>>> def f(z):
...     return z - (0.5 + 0.5j) 

我们将其封装为一个处理实部和虚部作为独立变量的实变量函数，返回实残差：

>>> def f_wrap(x):
...     fx = f(x[0] + 1j*x[1])
...     return np.array([fx.real, fx.imag]) 

因此，我们不再优化原始的 n 个复变量的 m-D 复杂函数，而是优化一个 2n 个实变量的 2m-D 实函数：

>>> from scipy.optimize import least_squares
>>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1]))
>>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j
>>> z
(0.49999999999925893+0.49999999999925893j)