案例系列：基于客户行为的贷款违约预测_决策树模型

最新推荐文章于 2024-04-04 16:04:31 发布
最新推荐文章于 2024-04-04 16:04:31 发布
阅读量1.6k 收藏 29
点赞数 10
分类专栏： 数据挖掘案例 数据挖掘 文章标签： 决策树 算法 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wjjc1017/article/details/135259718
版权
该博客围绕贷款违约风险预测展开，先介绍贷款、客户行为及分析相关概念，指出数据集问题与目标。接着进行数据清洗，包括检查清洁、随机欠采样等。然后开展数据分析，涵盖描述性、单变量、双变量和多元分析。最后进行数据预处理和建模、评分与评估，运用决策树算法预测违约风险。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

  • 1. | 引言
    • 1.1 | 什么是贷款？
    • 1.2 | 客户行为
    • 1.3 | 什么是客户行为分析？
    • 1.4 | 数据集问题
    • 1.5 | 如何符合个人贷款的资格
    • 1.6 | 笔记本目标
    • 1.7 | 数据集描述
    • 1.8 | 不平衡数据集的错误：
  • 2. | 导入库
    • 2.1 | 绘图函数
    • 2.2 | 统计函数
  • 3 | 阅读数据集
  • 4. | 数据清洗
    • 4.1 | 检查和清洁
    • 4.2 | 随机欠采样
    • 4.3 | 平均分配和相关
  • 5. | 数据分析
    • 5.1 | 描述性统计
    • 5.2 | 单变量分析
      • 5.2.1 | 数值列
        • 5.2.1.1 | 注释：
        • 5.2.1.2 | 注释：
        • 5.2.1.3 | 注释：
        • 5.2.1.4 | 注释：
        • 5.2.1.5 | 注释：
      • 5.2.2 | 分类列
    • 5.3 | 双变量分析
      • 5.3.1 | 什么是相关性？
      • 5.3.1 | 非参数秩相关
      • 5.3.1 | 数值列
      • 5.3.2 | 分类列
    • 5.4 | 多元分析
      • 5.4.1 | 分类列
      • 5.4.2 | 数值列
  • 6 | 数据预处理
    • 6.1 | 获取互信息
    • 6.2 | 特征选择
    • 6.3 | 分割数据集
  • 7 | 建模、评分和评估

1. | 引言

在这里插入图片描述

1.1 | 什么是贷款？

什么是贷款？

贷款的定义可以描述为将财产、金钱或其他物质商品交给另一方，以换取未来偿还贷款本金、利息和其他财务费用。贷款可以是特定的、一次性的金额，也可以作为开放式的信用额度提供。贷款有不同的形式，如个人贷款、商业贷款、有担保贷款和无担保贷款。

理解贷款

贷款是个人或某个实体所负的债务。交易中的另一方被称为贷方，通常是政府、金融机构或公司。他们向借款人借出所需的金额。作为回报，借款人同意根据最初借入的资金支付一定的条款，包括任何财务费用、利息等等。

贷款流程如何工作？

当您需要钱时，您向公司或银行申请贷款。您需要提供特定的细节，例如您为什么需要贷款，您必须披露您的财务历史、社会安全号码（SSN）和其他可能因贷款人而异的信息。

贷款人将审查您的申请并检查您的债务收入比以评估您是否能够偿还贷款。根据您的申请，贷款人将批准或拒绝申请。如果您的申请被拒绝，贷款人必须给出拒绝的原因。

如果您的申请被批准，您和贷款人之间将签订合同。贷款人将贷款金额转入您的账户，您需要偿还贷款金额以及利息和其他费用。

在签订合同并支付贷款之前，双方必须同意贷款的条款。在某些情况下，贷款人需要抵押品，其详细信息在贷款文件中有所涵盖。大多数贷款还规定了最高利率和还款期限。

为什么和何时提供贷款？

贷款出于多种原因而发放。借款人可能需要贷款购买物品、债务合并、创业、装修或投资。企业贷款可以帮助公司扩大业务。

简而言之，贷款允许经济中的货币总量增长，并通过向新企业借款开放竞争。贷款人（银行）从借款人那里收取的利息和其他费用是他们的收入来源。

在申请贷款时的一个重要因素

对于借款人来说，申请贷款时最重要的因素之一是利率。利率较高的贷款将给借款人带来更多的费用 - 他必须支付更高的月供或需要更长的时间来偿还贷款，相比之下，利率较低的贷款则相反。例如，如果您以4.5%的利率在5年期限内借款5000美元，您将需要在接下来的五年里每月支付93.22美元。然而，如果您的利率是9%，您将需要在同一期限内支付103.79美元。

让我们用不同的方式来理解。如果您贷款10000美元，利率为6%，并决定每月支付200美元，您需要支付58个月才能清偿贷款或余额。在利率为20%的情况下，与相同的余额和月供，需要108个月才能偿还贷款。

1.2 | 客户行为

客户行为是指个人的购买习惯，包括社会趋势、购买频率模式和影响他们购买决策的背景因素。企业研究客户行为，以了解他们的目标受众，并创建更具吸引力的产品和服务提供。

客户行为不仅描述谁在您的商店购物，还描述他们在您的商店如何购物。它涵盖了购物频率、产品偏好以及您的营销、销售和服务提供的感知等因素。了解这些细节有助于企业以一种富有成效和愉悦的方式与客户沟通。

客户行为受个人、心理和社会三个因素的影响。让我们深入了解每种类型。

1.3 | 什么是客户行为分析？

客户行为分析是对客户如何与您的公司互动的定性和定量观察。您首先将客户根据共同的兴趣分成不同的买家人物群体。然后，观察每个群体在其相应的客户旅程阶段中如何与您的公司互动。

这种分析可以洞察影响您的受众的变量以及客户在其旅程中考虑的动机、优先事项和决策方法。它还可以帮助您了解客户对您的公司的感受，以及这种感知是否与他们的核心价值观相一致。

1.4 | 数据集问题

一个组织希望预测消费者贷款产品的可能违约者。他们根据他们观察到的历史客户行为数据。因此，当他们获得新客户时，他们希望预测谁更有风险，谁不是。

1.5 | 如何符合个人贷款的资格

没有一个公式可以确定个人贷款的资格 - 每个申请人的财务状况都是不同和独特的。然而，有一些经验法则和建议可以帮助您提高个人贷款的资格。

大多数个人贷款机构会审查您的信用评分、信用历史、收入和债务收入比来确定您的资格。虽然每个贷款人对这些因素的最低要求各不相同，但我们的建议包括：

  • 最低信用评分为670。 保持至少670的信用评分将提高您的资格机会。然而，如果您希望获得最有利的条件，我们建议最低评分为720。
  • 稳定而持续的月收入。 最低收入要求在贷款人之间可能差异巨大，有些贷款人没有要求。然而，拥有稳定而持续的收入至少可以证明您能够支付每月的还款。
  • 债务收入比小于36%。 虽然有些贷款人会批准债务收入比高达50%的高素质申请人，但最好的目标是将债务收入比控制在36%以下，以提高您的资格机会。

由于每个贷款人都有自己的最低要求，所以在可能的情况下，最好进行预先资格审查，并与贷款人确认您需要达到的标准。这将确保您只申请符合您特定财务状况的贷款。

1.6 | 笔记本目标

本笔记本的目标是：

  • 客户行为和人口统计分析。
  • 预测谁更有风险，谁不是。

1.7 | 数据集描述

数据集中有12个变量

所有值都是在贷款申请时提供的。

列名描述类型
income用户的收入int
age用户的年龄int
experience用户的职业经验（年）int
profession职业string
married是否已婚string
house_ownership住房所有权（自有、租赁或其他）string
car_ownership是否拥有汽车string
risk_flag是否曾经违约string
currentjobyears目前工作的年限int
currenthouseyears目前居住地的年限int
city居住城市string
state居住州string

risk_flag表示过去是否有违约记录。
所有值都是在贷款申请时提供的。

1.8 | 不平衡数据集的错误：

  • 不要在过采样或欠采样的数据集上进行测试。
  • 如果要实施交叉验证，请记住在交叉验证期间对训练数据进行过采样或欠采样，而不是之前！
  • 不要使用准确率作为不平衡数据集的度量标准（通常会很高且误导），而应使用F1分数、精确度/召回率分数或混淆矩阵。
# --- Notebook Theme (codes from @vivek468 & @sonalisingh1411) ---

# 导入必要的库
from IPython.core.display import display, HTML, Javascript

# 定义颜色映射
color_map = ['#FBAD3C', '#FCC404']

# 设置提示文本颜色
prompt = color_map[-1]
# 设置主要颜色
main_color = color_map[0]
# 设置强调主要颜色
strong_main_color = color_map[1]
# 设置自定义颜色列表
custom_colors = [strong_main_color, main_color]

# 定义CSS样式
css_file = '''
div #notebook {
background-color: white;
line-height: 20px;
}

#notebook-container {
%s
margin-top: 2em;
padding-top: 2em;
border-top: 4px solid %s;
-webkit-box-shadow: 0px 0px 8px 2px rgba(224, 212, 226, 0.5);
    box-shadow: 0px 0px 8px 2px rgba(224, 212, 226, 0.5);
}

div .input {
margin-bottom: 1em;
}

.rendered_html h1, .rendered_html h2, .rendered_html h3, .rendered_html h4, .rendered_html h5, .rendered_html h6 {
color: %s;
font-weight: 600;
}

div.input_area {
border: none;
    background-color: %s;
    border-top: 2px solid %s;
}

div.input_prompt {
color: %s;
}

div.output_prompt {
color: %s; 
}

div.cell.selected:before, div.cell.selected.jupyter-soft-selected:before {
background: %s;
}

div.cell.selected, div.cell.selected.jupyter-soft-selected {
    border-color: %s;
}

.edit_mode div.cell.selected:before {
background: %s;
}

.edit_mode div.cell.selected {
border-color: %s;

}
'''

# 将十六进制颜色转换为RGB格式
def to_rgb(h): 
    return tuple(int(h[i:i+2], 16) for i in [0, 2, 4])

# 将主要颜色转换为RGBA格式
main_color_rgba = 'rgba(%s, %s, %s, 0.1)' % (to_rgb(main_color[1:]))
# 将CSS样式写入文件
open('notebook.css', 'w').write(css_file % ('width: 95%;', main_color, main_color, main_color_rgba, main_color,  main_color, prompt, main_color, main_color, main_color, main_color))

# 定义函数nb，用于显示Notebook主题
def nb(): 
    return HTML("<style>" + open("notebook.css", "r").read() + "</style>")

# 调用nb函数，显示Notebook主题
nb()

2. | 导入库

导入我们在这个研究中需要使用的库。

# 导入库
import os  # 用于操作系统相关的功能
import numpy as np  # 用于数值计算
import pandas as pd  # 用于数据处理和分析
import matplotlib.pyplot as plt  # 用于绘图
import seaborn as sns  # 用于绘图和数据可视化
import warnings  # 用于忽略警告
from scipy import stats  # 用于科学计算
from IPython.core.interactiveshell import InteractiveShell  # 用于交互式控制台

# 设置库的相关参数
warnings.simplefilter(action="ignore", category=FutureWarning)  # 忽略未来警告
warnings.simplefilter(action="ignore", category=Warning)  # 忽略警告
InteractiveShell.ast_node_interactivity = "all"  # 设置交互式控制台的行为
%matplotlib inline  # 设置绘图在notebook中显示
np.set_printoptions(suppress=True)  # 设置打印浮点数时不使用科学计数法

def set_seed(seed=42):
    np.random.seed(seed)  # 设置随机数种子
    os.environ["PYTHONHASHSEED"] = str(seed)  # 设置Python哈希种子
    
pd.set_option("display.width", 100)  # 设置显示宽度
pd.set_option("display.max_columns", 60)  # 设置显示的最大列数
pd.set_option("display.max_rows", 25)  # 设置显示的最大行数
pd.set_option("display.float_format", lambda x: "%.3f" % x)  # 设置浮点数的显示格式

2.1 | 绘图函数 


import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

def numerical_plotting(data, col, title, symb, ylabel, color):
    # 创建一个包含两个子图的画布
    fig, ax = plt.subplots(2, 1, 
                           sharex=True, 
                           figsize=(20, 8),
                           facecolor="#FFFFFF",
                           gridspec_kw={"height_ratios": (.2, .8)})
    
    # 设置子图的背景颜色为白色
    ax[0].set_facecolor("#FFFFFF")
    ax[1].set_facecolor("#FFFFFF")
    
    # 设置标题
    ax[0].set_title(title, 
                    weight="bold", 
                    fontsize=30, 
                    pad=30)
    
    # 绘制箱线图
    sns.boxplot(x=col, 
                data=data,
                color=color,
                ax=ax[0])
    
    # 设置y轴刻度为空
    ax[0].set(yticks=[])
    
    # 绘制数据的分布图
    sns.distplot(data[col], kde=True, color=color)
    
    # 设置x轴和y轴的刻度字体样式和大小
    plt.xticks(weight="bold", fontsize=10)
    plt.yticks(weight="bold", fontsize=10)
    
    # 设置子图的x轴和y轴标签
    ax[0].set_xlabel(col, weight="bold", fontsize=15, labelpad=15)
    ax[1].set_xlabel(col, weight="bold", fontsize=15)
    ax[1].set_ylabel(ylabel, weight="bold", fontsize=15)
    
    # 绘制均值线、中位数线、最大值线、最小值线和众数线
    plt.axvline(data[col].mean(), 
                color='darkgreen', 
                linewidth=2.2, 
                label='mean=' + str(np.round(data[col].mean(),1)) + symb)
    plt.axvline(data[col].median(), 
                color='red', 
                linewidth=2.2, 
                label='median='+ str(np.round(data[col].median(),1)) + symb)
    plt.axvline(data[col].max(), 
                color='blue', 
                linewidth=2.2, 
                label='max='+ str(np.round(data[col].max(),1)) + symb)
    plt.axvline(data[col].min(), 
                color='orange', 
                linewidth=2.2, 
                label='min='+ str(np.round(data[col].min(),1)) + symb)
    plt.axvline(data[col].mode()[0], 
                color='purple', 
                linewidth=2.2, 
                label='mode='+ str(data[col].mode()[0]) + symb)
    
    # 添加图例
    plt.legend(bbox_to_anchor=(1, 1), 
               ncol=1, 
               fontsize=17, 
               fancybox=True, 
               shadow=True, 
               frameon=False)
    
    # 调整子图布局
    plt.tight_layout()
    # 显示图像
    plt.show()

def count_pie_plot(datapie, datacount, colpiey, colcount, text1, text2, piecomap,
                   xlabel, ylabel, xticklabel, yticklabel, ystart, yend, pielabels, yplus, 
                   piefs=10, countcomap=None, pctdistance=0.65, fontsize=15, xtickrotation=None):
    # 创建一个包含两个子图的画布
    fig, (ax1, ax2) = plt.subplots(ncols=2, 
                                   nrows=1, 
                                   facecolor=("#FFFFFF"),
                                   figsize=(24, 8))
    
    # 绘制饼图
    datapie.plot(kind="pie", 
                 y=colpiey,
                 autopct='%1.1f%%',
                 labels=None,
                 startangle=90,
                 colors=piecomap,
                 wedgeprops=dict(width=0.15),
                 pctdistance=pctdistance,
                 fontsize=piefs,
                 ax=ax1,
                 textprops=dict(color="black", 
                                weight="bold"))
    
    # 绘制计数图
    sns.countplot(x=colcount,
                  data=datacount,
                  palette=countcomap,
                  ax=ax2)

    # 设置标题
    x0, x1 = ax1.get_xlim()
    y0, y1 = ax1.get_ylim()
    
    ax1.text(x0, y1 * 1.40, 
             text1, 
             fontsize=30, 
             ha="left", 
             va="center", 
             weight="bold")
    ax1.text(x0, y1 * 1.25, 
             text2, 
             fontsize=18, 
             ha="left", 
             va="center")
    
    # 添加饼图的图例
    ax1.legend(pielabels, 
               loc="upper left", 
               bbox_to_anchor=(x0*0.01, y1*0.85), 
               prop={'size': 10.5}, frameon=False, ncol=len(datapie))
    
    # 设置x轴和y轴标签
    ax2.set_xlabel(xlabel,
                   weight="bold",
                   labelpad=15,
                   fontsize=15)

    ax2.set_ylabel(ylabel,
                   weight="bold",
                   labelpad=15,
                   fontsize=15)

    # 设置x轴和y轴刻度标签的样式和大小
    ax2.set_xticklabels(labels=xticklabel,
                        weight="semibold",
                        fontsize=10,
                        rotation=xtickrotation)
    ax2.set_yticklabels(labels=yticklabel,
                        weight="semibold",
                        fontsize=10)

    # 绘制数据标签
    i=0
    for p in ax2.patches:
        value = f"{p.get_height()}"
        if (i < 2):
            y1 = -2
        else:
            y1 = 2
        i += 1
        x = p.get_x() + p.get_width() / 2 
        y = p.get_y() + p.get_height() + yplus
        ax2.text(x, y, value, ha="center", va="center", fontsize=15, weight="semibold") 

    # 设置y轴的范围
    ax2.set_ylim(ystart, yend)
    # 设置子图的背景颜色为白色
    ax2.set_facecolor("#FFFFFF")
    # 隐藏饼图的y轴标签
    ax1.set_ylabel(None)
    
    # 调整子图布局
    plt.tight_layout()
    # 返回画布
    return fig

def countplot_y(data, xplus, coly, sizey, text1, text2, 
                xlabel, ylabel, xstart, xend, ytimes1, ytimes2):
    # 创建一个包含一个子图的画布
    fig, ax = plt.subplots(ncols=1,
                           nrows=1,
                           facecolor=("#FFFFFF"),
                           figsize=(24, sizey))

    # 绘制计数图
    sns.countplot(y=coly,
                  data=data,
                  palette=['#E0144C', '#FF5858', '#3AB0FF', '#FFB562', '#6FEDD6', '#6D9885'],
                  ax=ax)

    # 设置标题
    x0, x1 = ax.get_xlim()
    y0, y1 = ax.get_ylim()

    ax.text(x0, y1 * ytimes1, 
            text1, fontsize=30, 
            ha="left", va="center", weight="bold")
    ax.text(x0, y1 * ytimes2, 
            text2, fontsize=18, 
            ha="left", va="center")

    # 设置x轴和y轴刻度标签的样式和大小
    plt.xticks(weight="bold",
               fontsize=10)
    plt.yticks(weight="bold",
               fontsize=10)
    plt.xlabel(xlabel, weight="bold", 
               fontsize=25, labelpad=20)
    plt.ylabel(ylabel, weight="bold", 
               fontsize=25, labelpad=20)

    # 绘制数据标签
    i=0
    for p in ax.patches:
        value = f'{p.get_width()}'
        if i < 7:
            x1 = -1.2
        else:
            x1 = 1.2

        i+=1
        x = p.get_x() + p.get_width() + xplus
        y = p.get_y() + p.get_height() -.4
        ax.text(x, y, value, ha='center', va='center', fontsize=15, weight='semibold') 

    # 调整子图布局
    plt.tight_layout()
    # 设置x轴的范围
    ax.set_xlim(xstart, xend)
    # 设置子图的背景颜色为白色
    ax.set_facecolor("#FFFFFF")
    
    # 返回画布
    return fig

def bivariate_numerical_plot(data, x, hue, title, xlabel, ylabel):
    # 创建一个包含一个子图的画布
    fig, ax = plt.subplots(1, 1,
                           figsize=(20, 6), 
                           facecolor="#FFFFFF")
    # 绘制双变量的核密度图
    sns.kdeplot(data=data, 
                x=x, 
                hue=hue, 
                fill=True)
    
    # 设置子图的背景颜色为白色
    ax.set_facecolor("#FFFFFF")
    
    # 设置标题
    plt.title(title, weight="bold", 
              fontsize=25, pad=30)
    plt.xticks(weight="bold", fontsize=10)
    plt.yticks(weight="bold", fontsize=10)
    plt.xlabel(xlabel, weight="bold", 
               fontsize=15, labelpad=15)
    plt.ylabel(ylabel, weight="bold", 
               fontsize=15, labelpad=15)
    # 调整子图布局
    plt.tight_layout()
    # 显示图像
    plt.show()

def mtvboxplot(data, x, y, hue, title, xlabel, ylabel):
    # 创建一个包含一个子图的画布
    fig, ax = plt.subplots(1, 1,
                           figsize=(24, 8))
    # 绘制箱线图
    sns.boxplot(x=x, y=y, hue=hue, 
                data=data, ax=ax)
    # 设置标题
    plt.title(title, weight="bold", 
              fontsize=25, pad=25)
    plt.xticks(weight="bold", fontsize=10)
    plt.yticks(weight="bold", fontsize=10)
    plt.xlabel(xlabel, weight="bold", 
               fontsize=15, labelpad=10)
    plt.ylabel(ylabel, weight="bold", 
               fontsize=15, labelpad=10)
    # 调整子图布局
    plt.tight_layout()
    # 显示图像
    plt.show()

2.2 | 统计函数 



# 定义函数spearman_correlation，用于计算Spearman相关系数并解释结果
def spearman_correlation(data1, data2, title):
    # 打印标题
    print("-" * 15, title, "-" * 15)
    print()
    
    # 计算Spearman相关系数
    coef, p = stats.spearmanr(data1, data2)
    print(f"Spearmans correlation coefficient: {coef:.3f}")
    print()
    
    # 解释结果的显著性
    alpha = 0.05
    if (p > alpha):
        print(f"Samples are uncorrelated (fail to reject H0) p={p:.3f}")
    else:
        print(f"Samples are correlated (reject H0) p={p:.3f}")
    print()

# 定义函数pearson_correlation，用于计算Pearson相关系数并解释结果
def pearson_correlation(data1, data2, title):
    # 打印标题
    print("-" * 15, title, "-" * 15)
    print()
    
    # 计算Pearson相关系数
    coef, p = stats.pearsonr(data1, data2)
    print(f"Pearson correlation coefficient: {coef:.3f}")
    print()
    
    # 解释结果的显著性
    alpha = 0.05
    if (p > alpha):
        print(f"Samples are uncorrelated (fail to reject H0) p={p:.3f}")
    else:
        print(f"Samples are correlated (reject H0) p={p:.3f}")
    print()

# 定义函数skew_kurtosis，用于计算偏度和峰度并解释结果
def skew_kurtosis(data, title):
    # 计算偏度和峰度
    skw = stats.skew(data, bias=False)
    kurt = stats.kurtosis(data, bias=False)
    
    # 打印标题
    print("-" * 20, title, "-" * 20)
    print(f"Skewness: {skw}")
    
    # 解释偏度的结果
    if (skw < -1) and (skw > 1):
        print("Highly skewed")
    elif (-1 < skw < -0.5) or (1 < skw < 0.5):
        print("Moderately skewed")
    elif (-0.5 < skw < 0.5):
        print("Approximately symmetric")
    
    print("-" * 35)
    print(f"Kurtosis: {kurt}")
    
    # 解释峰度的结果
    if (kurt > 1):
        print("The distribution is too peaked")
    elif (kurt < -1):
        print("The distribution is too flat")
    else:
        print("The distribution is non-normal")
    print("-" * 35)

# 定义函数chebychev，用于计算切比雪夫不等式并解释结果
def chebychev(data, title, interpret):
    # 计算均值和标准差
    mu = round(data.mean(), 1)
    s = round(data.std(), 1)
    
    # 计算切比雪夫不等式的上下限
    fc = round(mu - (2 * s), 1)
    sc = round(mu + (2 * s), 1)
    
    # 打印标题
    print("-" * 20, f"Interpretation of {title}", "-" * 20)
    print(f"first calc: {fc}")
    print(f"second calc: {sc}")
    print(interpret)
    print("-" * 40)

3 | 阅读数据集 

# 读取csv文件并设置索引列为"Id"，并删除含有缺失值的行
df = pd.read_csv("/kaggle/input/loan-prediction-based-on-customer-behavior/Training Data.csv", index_col="Id").dropna()
IncomeAgeExperienceMarried/SingleHouse_OwnershipCar_OwnershipProfessionCITYSTATECURRENT_JOB_YRSCURRENT_HOUSE_YRSRisk_Flag
Id
11303834233singlerentednoMechanical_engineerRewaMadhya_Pradesh3130
275745164010singlerentednoSoftware_DeveloperParbhaniMaharashtra9130
33991815664marriedrentednoTechnical_writerAlappuzhaKerala4100
46256451412singlerentedyesSoftware_DeveloperBhubaneswarOdisha2121
557688714711singlerentednoCivil_servantTiruchirappalli[10]Tamil_Nadu3141
.......................................
25199681548834313singlerentednoSurgeonKolkataWest_Bengal6110
25199728435722610singlerentednoArmy_officerRewaMadhya_Pradesh6110
2519984522448467singlerentednoDesign_EngineerKalyan-DombivliMaharashtra7120
2519996507128450singlerentednoGraphic_DesignerPondicherryPuducherry0100
25200090702307017singlerentednoStatisticianAvadiTamil_Nadu7110

252000 rows × 12 columns

3.1 | 检查数据集

# 使用df.info()方法获取数据框的信息

<class 'pandas.core.frame.DataFrame'>
Int64Index: 252000 entries, 1 to 252000
Data columns (total 12 columns):
 #   Column             Non-Null Count   Dtype 
---  ------             --------------   ----- 
 0   Income             252000 non-null  int64 
 1   Age                252000 non-null  int64 
 2   Experience         252000 non-null  int64 
 3   Married/Single     252000 non-null  object
 4   House_Ownership    252000 non-null  object
 5   Car_Ownership      252000 non-null  object
 6   Profession         252000 non-null  object
 7   CITY               252000 non-null  object
 8   STATE              252000 non-null  object
 9   CURRENT_JOB_YRS    252000 non-null  int64 
 10  CURRENT_HOUSE_YRS  252000 non-null  int64 
 11  Risk_Flag          252000 non-null  int64 
dtypes: int64(6), object(6)
memory usage: 25.0+ MB

There are 252,000个观测值和12个变量可用。

唯一性分类变量

让我们来看看分类变量。这些变量有多少个唯一值。

# 选择数据框中的分类和对象类型的列
categorical = df.select_dtypes(["category", "object"]).columns

# 遍历每个分类列
for cat_col in categorical:
    # 打印列名和该列的唯一值数量
    print(f"{cat_col}: {df[cat_col].nunique()} uniqueness variable")

Married/Single: 2 uniqueness variable
House_Ownership: 3 uniqueness variable
Car_Ownership: 2 uniqueness variable
Profession: 51 uniqueness variable
CITY: 317 uniqueness variable
STATE: 29 uniqueness variable

离散变量和连续变量让我们来看一下。

# 选择数据框中的数值类型列
numeric = df.select_dtypes(["int", "float"]).columns

# 遍历数值类型列
for num_col in numeric:
    # 输出该列的名称和唯一值的数量
    print(f"{num_col}: {df[num_col].nunique()} uniqueness variable")

Income: 41920 uniqueness variable
Age: 59 uniqueness variable
Experience: 21 uniqueness variable
CURRENT_JOB_YRS: 15 uniqueness variable
CURRENT_HOUSE_YRS: 5 uniqueness variable
Risk_Flag: 2 uniqueness variable

我们有多少缺失数据点？

让我们看看每列中有多少缺失数据…

# 获取每列缺失数据的数量
missing_values_count = df.isnull().sum()

# 查看前十列的缺失数据情况
missing_values_count[:10]

Income             0
Age                0
Experience         0
Married/Single     0
House_Ownership    0
Car_Ownership      0
Profession         0
CITY               0
STATE              0
CURRENT_JOB_YRS    0
dtype: int64

太好了！没有缺失值！让我们看看分类数据中的唯一变量！

# 获取数据框df中Profession列的唯一值列表
df.Profession.unique()

array(['Mechanical_engineer', 'Software_Developer', 'Technical_writer',
       'Civil_servant', 'Librarian', 'Economist', 'Flight_attendant',
       'Architect', 'Designer', 'Physician', 'Financial_Analyst',
       'Air_traffic_controller', 'Politician', 'Police_officer', 'Artist',
       'Surveyor', 'Design_Engineer', 'Chemical_engineer',
       'Hotel_Manager', 'Dentist', 'Comedian', 'Biomedical_Engineer',
       'Graphic_Designer', 'Computer_hardware_engineer',
       'Petroleum_Engineer', 'Secretary', 'Computer_operator',
       'Chartered_Accountant', 'Technician', 'Microbiologist',
       'Fashion_Designer', 'Aviator', 'Psychologist', 'Magistrate',
       'Lawyer', 'Firefighter', 'Engineer', 'Official', 'Analyst',
       'Geologist', 'Drafter', 'Statistician', 'Web_designer',
       'Consultant', 'Chef', 'Army_officer', 'Surgeon', 'Scientist',
       'Civil_engineer', 'Industrial_Engineer', 'Technology_specialist'],
      dtype=object)

# 获取df中CITY列的唯一值列表
df.CITY.unique()

array(['Rewa', 'Parbhani', 'Alappuzha', 'Bhubaneswar',
       'Tiruchirappalli[10]', 'Jalgaon', 'Tiruppur', 'Jamnagar',
       'Kota[6]', 'Karimnagar', 'Hajipur[31]', 'Adoni', 'Erode[17]',
       'Kollam', 'Madurai', 'Anantapuram[24]', 'Kamarhati', 'Bhusawal',
       'Sirsa', 'Amaravati', 'Secunderabad', 'Ahmedabad', 'Ajmer',
       'Ongole', 'Miryalaguda', 'Ambattur', 'Indore', 'Pondicherry',
       'Shimoga', 'Chennai', 'Gulbarga', 'Khammam', 'Saharanpur',
       'Gopalpur', 'Amravati', 'Udupi', 'Howrah', 'Aurangabad[39]',
       'Hospet', 'Shimla', 'Khandwa', 'Bidhannagar', 'Bellary', 'Danapur',
       'Purnia[26]', 'Bijapur', 'Patiala', 'Malda', 'Sagar', 'Durgapur',
       'Junagadh', 'Singrauli', 'Agartala', 'Thanjavur', 'Hindupur',
       'Naihati', 'North_Dumdum', 'Panchkula', 'Anantapur', 'Serampore',
       'Bathinda', 'Nadiad', 'Kanpur', 'Haridwar', 'Berhampur',
       'Jamshedpur', 'Hyderabad', 'Bidar', 'Kottayam', 'Solapur',
       'Suryapet', 'Aizawl', 'Asansol', 'Deoghar', 'Eluru[25]',
       'Ulhasnagar', 'Aligarh', 'South_Dumdum', 'Berhampore',
       'Gandhinagar', 'Sonipat', 'Muzaffarpur', 'Raichur',
       'Rajpur_Sonarpur', 'Ambarnath', 'Katihar', 'Kozhikode', 'Vellore',
       'Malegaon', 'Kochi', 'Nagaon', 'Nagpur', 'Srinagar', 'Davanagere',
       'Bhagalpur', 'Siwan[32]', 'Meerut', 'Dindigul', 'Bhatpara',
       'Ghaziabad', 'Kulti', 'Chapra', 'Dibrugarh', 'Panihati',
       'Bhiwandi', 'Morbi', 'Kalyan-Dombivli', 'Gorakhpur', 'Panvel',
       'Siliguri', 'Bongaigaon', 'Patna', 'Ramgarh', 'Ozhukarai',
       'Mirzapur', 'Akola', 'Satna', 'Motihari[34]', 'Jalna', 'Jalandhar',
       'Unnao', 'Karnal', 'Cuttack', 'Proddatur', 'Ichalkaranji',
       'Warangal[11][12]', 'Jhansi', 'Bulandshahr', 'Narasaraopet',
       'Chinsurah', 'Jehanabad[38]', 'Dhanbad', 'Gudivada', 'Gandhidham',
       'Raiganj', 'Kishanganj[35]', 'Varanasi', 'Belgaum',
       'Tirupati[21][22]', 'Tumkur', 'Coimbatore', 'Kurnool[18]',
       'Gurgaon', 'Muzaffarnagar', 'Aurangabad', 'Bhavnagar', 'Arrah',
       'Munger', 'Tirunelveli', 'Mumbai', 'Mango', 'Nashik', 'Kadapa[23]',
       'Amritsar', 'Khora,_Ghaziabad', 'Ambala', 'Agra', 'Ratlam',
       'Surendranagar_Dudhrej', 'Delhi_city', 'Bhopal', 'Hapur', 'Rohtak',
       'Durg', 'Korba', 'Bangalore', 'Shivpuri', 'Thrissur',
       'Vijayanagaram', 'Farrukhabad', 'Nangloi_Jat', 'Madanapalle',
       'Thoothukudi', 'Nagercoil', 'Gaya', 'Chandigarh_city', 'Jammu[16]',
       'Kakinada', 'Dewas', 'Bhalswa_Jahangir_Pur', 'Baranagar',
       'Firozabad', 'Phusro', 'Allahabad', 'Guna', 'Thane', 'Etawah',
       'Vasai-Virar', 'Pallavaram', 'Morena', 'Ballia', 'Surat',
       'Burhanpur', 'Phagwara', 'Mau', 'Mangalore', 'Alwar',
       'Mahbubnagar', 'Maheshtala', 'Hazaribagh', 'Bihar_Sharif',
       'Faridabad', 'Lucknow', 'Tenali', 'Barasat', 'Amroha', 'Giridih',
       'Begusarai', 'Medininagar', 'Rajahmundry[19][20]', 'Saharsa[29]',
       'New_Delhi', 'Bhilai', 'Moradabad', 'Machilipatnam',
       'Mira-Bhayandar', 'Pali', 'Navi_Mumbai', 'Mehsana', 'Imphal',
       'Kolkata', 'Sambalpur', 'Ujjain', 'Madhyamgram', 'Jabalpur',
       'Jamalpur[36]', 'Ludhiana', 'Bareilly', 'Gangtok', 'Anand',
       'Dehradun', 'Pune', 'Satara', 'Srikakulam', 'Raipur', 'Jodhpur',
       'Darbhanga', 'Nizamabad', 'Nandyal', 'Dehri[30]', 'Jorhat',
       'Ranchi', 'Kumbakonam', 'Guntakal', 'Haldia', 'Loni',
       'Pimpri-Chinchwad', 'Rajkot', 'Nanded', 'Noida',
       'Kirari_Suleman_Nagar', 'Jaunpur', 'Bilaspur', 'Sambhal', 'Dhule',
       'Rourkela', 'Thiruvananthapuram', 'Dharmavaram', 'Nellore[14][15]',
       'Visakhapatnam[4]', 'Karawal_Nagar', 'Jaipur', 'Avadi',
       'Bhimavaram', 'Bardhaman', 'Silchar', 'Buxar[37]', 'Kavali',
       'Tezpur', 'Ramagundam[27]', 'Yamunanagar', 'Sri_Ganganagar',
       'Sasaram[30]', 'Sikar', 'Bally', 'Bhiwani', 'Rampur', 'Uluberia',
       'Sangli-Miraj_&_Kupwad', 'Hosur', 'Bikaner', 'Shahjahanpur',
       'Sultan_Pur_Majra', 'Vijayawada', 'Bharatpur', 'Tadepalligudem',
       'Tinsukia', 'Salem', 'Mathura', 'Guntur[13]', 'Hubli–Dharwad',
       'Guwahati', 'Chittoor[28]', 'Tiruvottiyur', 'Vadodara',
       'Ahmednagar', 'Fatehpur', 'Bhilwara', 'Kharagpur', 'Bettiah[33]',
       'Bhind', 'Bokaro', 'Karaikudi', 'Raebareli', 'Pudukkottai',
       'Udaipur', 'Mysore[7][8][9]', 'Panipat', 'Latur', 'Tadipatri',
       'Bahraich', 'Orai', 'Raurkela_Industrial_Township', 'Gwalior',
       'Katni', 'Chandrapur', 'Kolhapur'], dtype=object)

# 获取df中STATE列的唯一值列表
df.STATE.unique()

array(['Madhya_Pradesh', 'Maharashtra', 'Kerala', 'Odisha', 'Tamil_Nadu',
       'Gujarat', 'Rajasthan', 'Telangana', 'Bihar', 'Andhra_Pradesh',
       'West_Bengal', 'Haryana', 'Puducherry', 'Karnataka',
       'Uttar_Pradesh', 'Himachal_Pradesh', 'Punjab', 'Tripura',
       'Uttarakhand', 'Jharkhand', 'Mizoram', 'Assam',
       'Jammu_and_Kashmir', 'Delhi', 'Chhattisgarh', 'Chandigarh',
       'Uttar_Pradesh[5]', 'Manipur', 'Sikkim'], dtype=object)
注意：

  1. 我们可以看到上面有许多带有括号和数字的城市名称和州名，它们的含义不太清楚，让我们稍后清理一下。

  2. 这个数据集的列非常不一致和整洁，这可能会在未来造成混淆或打字错误，让我们进行更改，以便于后续更容易地分析和预测。

4. | 数据清洗

4.1 | 检查和清洁 

# 获取DataFrame的列名
df.columns

Index(['Income', 'Age', 'Experience', 'Married/Single', 'House_Ownership', 'Car_Ownership',
       'Profession', 'CITY', 'STATE', 'CURRENT_JOB_YRS', 'CURRENT_HOUSE_YRS', 'Risk_Flag'],
      dtype='object')

# 将df的列名转换为小写字母形式
df.columns = df.columns.str.lower()

Index(['income', 'age', 'experience', 'married/single', 'house_ownership', 'car_ownership',
       'profession', 'city', 'state', 'current_job_yrs', 'current_house_yrs', 'risk_flag'],
      dtype='object')

# 将"married/single"列重命名为"married_single"列，并在原数据框上进行修改
df.rename(columns={"married/single": "married_single"}, inplace=True)

# 获取数据框的列名
df.columns

Index(['income', 'age', 'experience', 'married_single', 'house_ownership', 'car_ownership',
       'profession', 'city', 'state', 'current_job_yrs', 'current_house_yrs', 'risk_flag'],
      dtype='object')

太好了！现在进入城市和州变量，让我们清理字符！

# 将df中的city列的值提取出只包含字母的部分，并赋值给df的city列
df.city = df.city.str.extract("([A-Za-z]+)")

# 获取df中city列的唯一值，并返回一个数组

array(['Rewa', 'Parbhani', 'Alappuzha', 'Bhubaneswar', 'Tiruchirappalli',
       'Jalgaon', 'Tiruppur', 'Jamnagar', 'Kota', 'Karimnagar', 'Hajipur',
       'Adoni', 'Erode', 'Kollam', 'Madurai', 'Anantapuram', 'Kamarhati',
       'Bhusawal', 'Sirsa', 'Amaravati', 'Secunderabad', 'Ahmedabad',
       'Ajmer', 'Ongole', 'Miryalaguda', 'Ambattur', 'Indore',
       'Pondicherry', 'Shimoga', 'Chennai', 'Gulbarga', 'Khammam',
       'Saharanpur', 'Gopalpur', 'Amravati', 'Udupi', 'Howrah',
       'Aurangabad', 'Hospet', 'Shimla', 'Khandwa', 'Bidhannagar',
       'Bellary', 'Danapur', 'Purnia', 'Bijapur', 'Patiala', 'Malda',
       'Sagar', 'Durgapur', 'Junagadh', 'Singrauli', 'Agartala',
       'Thanjavur', 'Hindupur', 'Naihati', 'North', 'Panchkula',
       'Anantapur', 'Serampore', 'Bathinda', 'Nadiad', 'Kanpur',
       'Haridwar', 'Berhampur', 'Jamshedpur', 'Hyderabad', 'Bidar',
       'Kottayam', 'Solapur', 'Suryapet', 'Aizawl', 'Asansol', 'Deoghar',
       'Eluru', 'Ulhasnagar', 'Aligarh', 'South', 'Berhampore',
       'Gandhinagar', 'Sonipat', 'Muzaffarpur', 'Raichur', 'Rajpur',
       'Ambarnath', 'Katihar', 'Kozhikode', 'Vellore', 'Malegaon',
       'Kochi', 'Nagaon', 'Nagpur', 'Srinagar', 'Davanagere', 'Bhagalpur',
       'Siwan', 'Meerut', 'Dindigul', 'Bhatpara', 'Ghaziabad', 'Kulti',
       'Chapra', 'Dibrugarh', 'Panihati', 'Bhiwandi', 'Morbi', 'Kalyan',
       'Gorakhpur', 'Panvel', 'Siliguri', 'Bongaigaon', 'Patna',
       'Ramgarh', 'Ozhukarai', 'Mirzapur', 'Akola', 'Satna', 'Motihari',
       'Jalna', 'Jalandhar', 'Unnao', 'Karnal', 'Cuttack', 'Proddatur',
       'Ichalkaranji', 'Warangal', 'Jhansi', 'Bulandshahr',
       'Narasaraopet', 'Chinsurah', 'Jehanabad', 'Dhanbad', 'Gudivada',
       'Gandhidham', 'Raiganj', 'Kishanganj', 'Varanasi', 'Belgaum',
       'Tirupati', 'Tumkur', 'Coimbatore', 'Kurnool', 'Gurgaon',
       'Muzaffarnagar', 'Bhavnagar', 'Arrah', 'Munger', 'Tirunelveli',
       'Mumbai', 'Mango', 'Nashik', 'Kadapa', 'Amritsar', 'Khora',
       'Ambala', 'Agra', 'Ratlam', 'Surendranagar', 'Delhi', 'Bhopal',
       'Hapur', 'Rohtak', 'Durg', 'Korba', 'Bangalore', 'Shivpuri',
       'Thrissur', 'Vijayanagaram', 'Farrukhabad', 'Nangloi',
       'Madanapalle', 'Thoothukudi', 'Nagercoil', 'Gaya', 'Chandigarh',
       'Jammu', 'Kakinada', 'Dewas', 'Bhalswa', 'Baranagar', 'Firozabad',
       'Phusro', 'Allahabad', 'Guna', 'Thane', 'Etawah', 'Vasai',
       'Pallavaram', 'Morena', 'Ballia', 'Surat', 'Burhanpur', 'Phagwara',
       'Mau', 'Mangalore', 'Alwar', 'Mahbubnagar', 'Maheshtala',
       'Hazaribagh', 'Bihar', 'Faridabad', 'Lucknow', 'Tenali', 'Barasat',
       'Amroha', 'Giridih', 'Begusarai', 'Medininagar', 'Rajahmundry',
       'Saharsa', 'New', 'Bhilai', 'Moradabad', 'Machilipatnam', 'Mira',
       'Pali', 'Navi', 'Mehsana', 'Imphal', 'Kolkata', 'Sambalpur',
       'Ujjain', 'Madhyamgram', 'Jabalpur', 'Jamalpur', 'Ludhiana',
       'Bareilly', 'Gangtok', 'Anand', 'Dehradun', 'Pune', 'Satara',
       'Srikakulam', 'Raipur', 'Jodhpur', 'Darbhanga', 'Nizamabad',
       'Nandyal', 'Dehri', 'Jorhat', 'Ranchi', 'Kumbakonam', 'Guntakal',
       'Haldia', 'Loni', 'Pimpri', 'Rajkot', 'Nanded', 'Noida', 'Kirari',
       'Jaunpur', 'Bilaspur', 'Sambhal', 'Dhule', 'Rourkela',
       'Thiruvananthapuram', 'Dharmavaram', 'Nellore', 'Visakhapatnam',
       'Karawal', 'Jaipur', 'Avadi', 'Bhimavaram', 'Bardhaman', 'Silchar',
       'Buxar', 'Kavali', 'Tezpur', 'Ramagundam', 'Yamunanagar', 'Sri',
       'Sasaram', 'Sikar', 'Bally', 'Bhiwani', 'Rampur', 'Uluberia',
       'Sangli', 'Hosur', 'Bikaner', 'Shahjahanpur', 'Sultan',
       'Vijayawada', 'Bharatpur', 'Tadepalligudem', 'Tinsukia', 'Salem',
       'Mathura', 'Guntur', 'Hubli', 'Guwahati', 'Chittoor',
       'Tiruvottiyur', 'Vadodara', 'Ahmednagar', 'Fatehpur', 'Bhilwara',
       'Kharagpur', 'Bettiah', 'Bhind', 'Bokaro', 'Karaikudi',
       'Raebareli', 'Pudukkottai', 'Udaipur', 'Mysore', 'Panipat',
       'Latur', 'Tadipatri', 'Bahraich', 'Orai', 'Raurkela', 'Gwalior',
       'Katni', 'Chandrapur', 'Kolhapur'], dtype=object)

太棒了！现在是状态变量。

# 将df中的state列的值提取出来，只保留由字母组成的部分
df.state = df.state.str.extract("([A-Za-z]+)")

# 获取df中state列的唯一值，并返回一个数组
df.state.unique()

array(['Madhya', 'Maharashtra', 'Kerala', 'Odisha', 'Tamil', 'Gujarat',
       'Rajasthan', 'Telangana', 'Bihar', 'Andhra', 'West', 'Haryana',
       'Puducherry', 'Karnataka', 'Uttar', 'Himachal', 'Punjab',
       'Tripura', 'Uttarakhand', 'Jharkhand', 'Mizoram', 'Assam', 'Jammu',
       'Delhi', 'Chhattisgarh', 'Chandigarh', 'Manipur', 'Sikkim'],
      dtype=object)

4.2 | 随机欠采样 

# 对于高度倾斜的类别，我们应该使它们等价，以便具有类别的正常分布。
# 在创建子样本之前，让我们对数据进行洗牌
df = df.sample(frac=1)

# 欺诈类别的数量为492行。
risk_data = df.loc[df["risk_flag"] == 1]
not_risk_data = df.loc[df["risk_flag"] == 0][:30996]

# 将风险和非风险数据合并
normal_distributed_data = pd.concat([risk_data, not_risk_data])

# 对数据行进行洗牌
loan = normal_distributed_data.sample(frac=1, random_state=42)

# 打印前几行数据
loan.head()
incomeageexperiencemarried_singlehouse_ownershipcar_ownershipprofessioncitystatecurrent_job_yrscurrent_house_yrsrisk_flag
Id
23747736017739singlerentednoCivil_engineerPanchkulaHaryana4110
1867286000177701singlerentednoHotel_ManagerFaridabadHaryana1140
955789774160249singlerentedyesMechanical_engineerMalegaonMaharashtra9120
2490111649795295singlerentedyesPetroleum_EngineerGhaziabadUttar3141
1042410675231singlerentedyesGraphic_DesignerHyderabadTelangana1141

4.3 | 平均分配和相关 

# 打印子样本数据集中风险标志的分布
print("Distribution of the risk_flag in the subsample dataset")

# 计算风险标志的值计数并除以数据集的长度，得到风险标志的分布比例
print(loan["risk_flag"].value_counts() / len(loan))

# 使用sns库的countplot函数绘制风险标志的计数柱状图
sns.countplot("risk_flag", data=loan)

# 设置图表标题为"Equally Distributed Risk Flag"，字体大小为14
plt.title('Equally Distributed Risk Flag', fontsize=14);

Distribution of the risk_flag in the subsample dataset
0   0.500
1   0.500
Name: risk_flag, dtype: float64

现在我们的数据框已经正确平衡，我们可以进一步进行分析和数据预处理。

5. | 数据分析

5.1 | 描述性统计 

# 对loan数据集进行描述性统计分析，排除数值类型的列
loan.describe(exclude=[np.number])
married_singlehouse_ownershipcar_ownershipprofessioncitystate
count619926199261992619926199261992
unique2325131628
topsinglerentednoPhysicianSrinagarUttar
freq56106575404401514713517036
# 对loan数据集进行描述性统计分析，只包括数值类型的列
loan.describe(include=[np.number])
incomeageexperiencecurrent_job_yrscurrent_house_yrsrisk_flag
count61992.00061992.00061992.00061992.00061992.00061992.000
mean4985049.95749.4689.8336.25211.9930.500
std2894816.28317.2156.0473.6941.3980.500
min10310.00021.0000.0000.00010.0000.000
25%2467224.00034.0005.0003.00011.0000.000
50%4995211.00049.00010.0006.00012.0000.500
75%7511735.00064.00015.0009.00013.0001.000
max9999180.00079.00020.00014.00014.0001.000


# 对职业进行分组，并计算其收入的最小值、最大值和平均值,按照最大值的降序对结果进行排序,对结果进行转置
loan.groupby("profession")["income"].agg(["min", "max", "mean"]).sort_values(by="max", ascending=False).T
professionDrafterSecretaryComputer_hardware_engineerAnalystOfficialSurgeonPolice_officerBiomedical_EngineerPhysicianIndustrial_EngineerPsychologistComedianTechnology_specialistEngineerHotel_ManagerDentistTechnicianMagistrateWeb_designerAir_traffic_controllerCivil_engineerStatisticianDesignerArtistLawyerAviatorArchitectFirefighterGraphic_DesignerFinancial_AnalystMechanical_engineerScientistGeologistConsultantArmy_officerChartered_AccountantMicrobiologistSoftware_DeveloperSurveyorCivil_servantChemical_engineerComputer_operatorPoliticianTechnical_writerFlight_attendantChefEconomistFashion_DesignerDesign_EngineerLibrarianPetroleum_Engineer
min64805.00084491.00087298.00040073.000212833.00018215.00013220.00019472.00012608.00021995.00070387.00013429.00041041.00010310.00017801.00069549.00016045.00067459.00057769.00024310.00036017.00046244.00092747.00031297.00064122.000130180.00025096.00029380.00010675.00080183.00037057.00028561.00062100.00028519.00012902.00023621.00043418.00066912.00011114.00011430.00026926.00041719.00098356.00023709.00011695.00015016.00016890.00012766.00053886.00059715.00080603.000
max9999180.0009998070.0009996192.0009993798.0009991569.0009990973.0009987955.0009987812.0009987805.0009986330.0009985964.0009984878.0009984686.0009983889.0009983764.0009982690.0009982680.0009982430.0009980350.0009979373.0009979065.0009978516.0009978110.0009976619.0009976302.0009975199.0009974540.0009974101.0009973420.0009972303.0009971347.0009970052.0009969924.0009967854.0009967074.0009964427.0009962662.0009962479.0009961107.0009951052.0009947148.0009946468.0009945612.0009945173.0009939884.0009935369.0009932245.0009915463.0009913743.0009908353.0009904501.000
mean4342734.9095419069.2535350469.0214948887.4214681748.9075032404.2604487583.6825239234.6454793578.1634943057.9465279403.1775167709.2105007861.1854700969.6924854616.4724898449.7465234049.4874666459.0205139463.8024856526.6135087931.2504946376.5145374355.0304954792.8515125980.0445086028.5305148845.1494938910.7054561209.6924781236.1844894524.2735688722.9264744364.9714655325.3935558590.5945256303.2654911007.3754570556.3295302379.6404833599.5955465939.7994917283.9044700907.1785040013.3574699706.2844980297.5724980862.8655051549.1334701768.6644864104.8275315121.690
# 对数据集loan按照"city"进行分组, 将排序结果转换为DataFrame，并进行转置
loan.groupby(["city"]).risk_flag.apply(lambda x: (x.sum() / x.size) * 100).sort_values(ascending=False).to_frame().T
cityBhubaneswarBarasatGwaliorKochiSatnaMuzaffarnagarPurniaAhmedabadMysoreSikarKottayamKavaliRaiganjBettiahBuxarGandhidhamMathuraShahjahanpurGhaziabadImphalBardhamanTinsukiaBidhannagarMangoIndoreRatlamUdaipurAmravatiRamagundamMoradabad...KozhikodeOraiRaichurKaraikudiNewLucknowTirunelveliKhoraAhmednagarKumbakonamGangtokWarangalHosurBhagalpurBareillyNoidaBelgaumKatniPanihatiTadipatriBangaloreMiraMehsanaBerhampurRajpurBijapurSultanLaturDehradunGandhinagar
risk_flag79.51873.83572.41472.32171.38570.91869.41269.27168.48768.45968.28468.01567.98467.77866.86266.53166.36466.09265.99365.59165.08664.91964.11164.10363.66463.46962.90362.75562.70562.694...32.39432.12131.81831.76531.76031.25030.76929.94728.57128.40228.28328.09027.35025.86225.28724.52824.44423.86423.83723.00922.88122.68922.66722.41422.05921.73920.00019.65818.69916.505

1 rows × 316 columns

# 对数据集loan按照"state"进行分组, 将结果转换为DataFrame，并进行转置
loan.groupby("state").risk_flag.apply(lambda x: (x.sum() / x.size) * 100).sort_values(ascending=False).to_frame().T
stateManipurTripuraKeralaJammuMadhyaOdishaChhattisgarhRajasthanJharkhandAssamHimachalTelanganaBiharHaryanaWestUttarAndhraPuducherryMaharashtraGujaratMizoramChandigarhDelhiKarnatakaTamilPunjabUttarakhandSikkim
risk_flag65.59162.10058.54057.17256.97954.74053.78953.01652.04751.98451.62851.44551.40350.77750.62248.89148.40048.26648.12248.03347.23646.21245.66445.12344.76540.17036.43828.283
# 对贷款数据按照职业进行分组,对每个职业的风险标志进行计算，得到每个职业的平均风险百分比,对每个职业的平均风险百分比进行降序排序，并转换为DataFrame格式
loan.groupby("profession").risk_flag.apply(lambda x: (x.sum() / x.size) * 100).sort_values(ascending=False).to_frame().T
professionPolice_officerSoftware_DeveloperSurveyorChartered_AccountantArmy_officerScientistGeologistOfficialFirefighterTechnical_writerCivil_engineerBiomedical_EngineerTechnicianArchitectHotel_ManagerAviatorAir_traffic_controllerSecretaryFlight_attendantArtistComputer_hardware_engineerMagistrateConsultantLawyerComputer_operatorMicrobiologistFashion_DesignerGraphic_DesignerPsychologistEngineerAnalystChefSurgeonComedianDentistPhysicianCivil_servantLibrarianChemical_engineerStatisticianDrafterPoliticianWeb_designerDesignerMechanical_engineerDesign_EngineerFinancial_AnalystEconomistIndustrial_EngineerPetroleum_EngineerTechnology_specialist
risk_flag59.89856.51856.17655.51155.13254.67554.31154.25253.77953.28753.00152.69952.57052.49152.15852.15351.92451.88751.67150.89750.58750.47150.29250.04049.75949.59249.43549.09448.99348.82548.67048.61848.37648.34748.33948.26648.11747.62347.00646.95646.68246.67846.56146.39646.19045.83345.20844.16343.89840.24438.332
# 对数据集loan按照"married_single"列进行分组
loan.groupby("married_single").risk_flag.apply(
    lambda x: (x.sum() / x.size) * 100  # 计算每个分组中风险标志的平均百分比
).sort_values(ascending=False).to_frame().T  # 将结果转换为DataFrame并进行转置操作
married_singlesinglemarried
risk_flag50.54744.784
# 导入了一个名为loan的数据集
# 对数据集进行了按照“car_ownership”列进行分组的操作
# 对每个分组中的“risk_flag”列进行了计算，计算方式是该列中1出现的次数占总数的比例，再乘以100
# 对计算结果进行了降序排列
# 将结果转换为DataFrame格式，并进行了转置操作
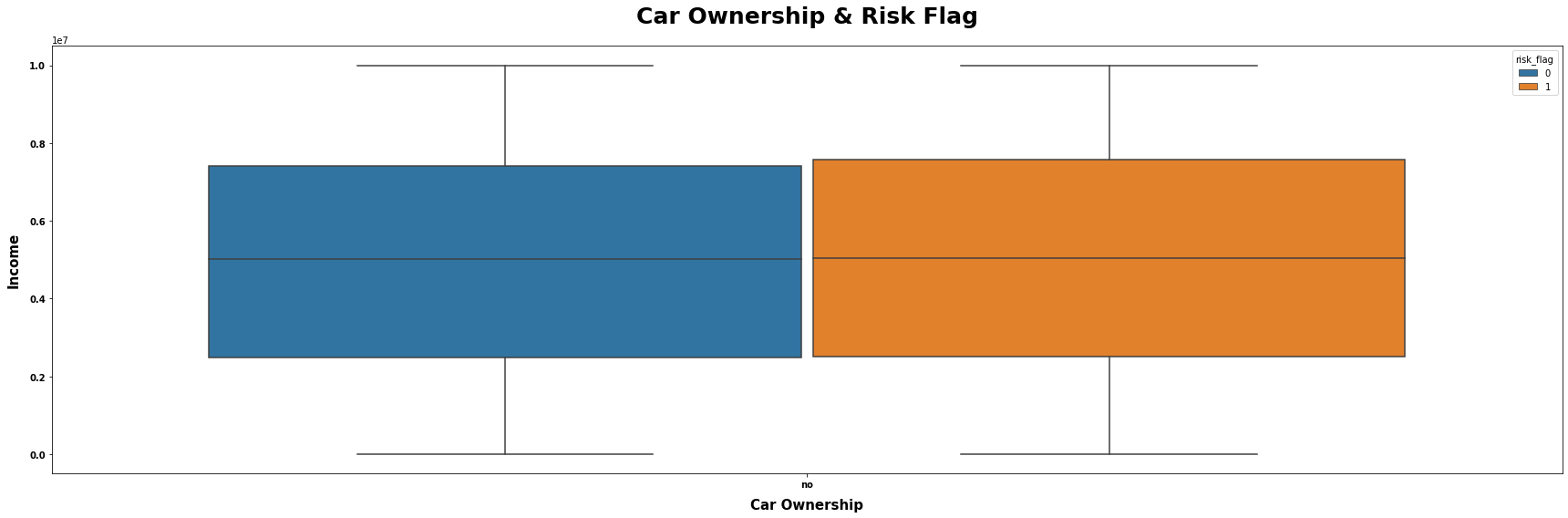
loan.groupby("car_ownership").risk_flag.apply(lambda x: (x.sum() / x.size) * 100).sort_values(ascending=False).to_frame().T
car_ownershipnoyes
risk_flag51.25846.921

5.1.1 | 结论

  • 平均收入前5的职业：

职业最小值最大值平均值
制图员6480599991804377671.407
秘书8449199980705414039.668
计算机硬件工程师8729899945015444923.183
分析师7166699921334919341.731
官员13202899915694650841.535

  • 城市风险标志平均百分比前5的城市：

城市风险标志平均百分比
布巴内斯瓦尔 75 % 75\% 75%
贝蒂亚 73.4 % 73.4\% 73.4%
瓜廖尔 71.7 % 71.7\% 71.7%
卡瓦利 71.4 % 71.4\% 71.4%
巴尔德汉 71.2 % 71.2\% 71.2%

  • 州风险标志平均百分比前5的州：

州风险标志平均百分比
曼尼普尔 67.5 % 67.5\% 67.5%
喀拉拉邦 57.5 % 57.5\% 57.5%
特里普拉 56.9 % 56.9\% 56.9%
中央邦 56.5 % 56.5\% 56.5%
查谟 56.3 % 56.3\% 56.3%

  • 职业风险标志平均百分比前5的职业：

职业风险标志平均百分比
警察 59 % 59\% 59%
软件开发人员 56.0 % 56.0\% 56.0%
军官 55.5 % 55.5\% 55.5%
注册会计师 55.5 % 55.5\% 55.5%
地质学家 55.2 % 55.2\% 55.2%

  • 客户是否已婚或单身的平均风险百分比：

M/S风险标志平均百分比
单身 50.5 % 50.5\% 50.5%
已婚 45.1 % 45.1\% 45.1%

  • 客户是否拥有汽车的平均风险百分比：

Y/N风险标志平均百分比
否 51.2 % 51.2\% 51.2%
是 46.9 46.9% 46.9

5.2 | 单变量分析

快速回顾

切比雪夫定理

1 − 1 k 2 : k = 2 − > 1 − 1 2 2 = 3 4 − > 75 k = 3 − > 1 − 1 3 2 = 8 9 − > 88.9 \begin{aligned} 1 - \frac{1}{k^2}: k &= 2 -> 1 - \frac{1}{2^2} = \frac{3}{4} -> 75 \\ k &= 3 -> 1 - \frac{1}{3^2} = \frac{8}{9} -> 88.9 \end{aligned} 1−k21​:kk​=2−>1−221​=43​−>75=3−>1−321​=98​−>88.9​


如何找到标准差 ($\sigma$)?

这是公式:

σ = σ 2 = ∑ ( x − μ ) 2 N s = s 2 = ∑ ( x − x ˉ ) 2 n − 1 \begin{aligned} \sigma &= \sqrt{\sigma^2} = \sqrt{\frac{\sum{(x - \mu)^2}}{N}} \\ s &= \sqrt{s^2} = \sqrt{\frac{\sum{(x - \bar{x})^2}}{n - 1}} \end{aligned} σs​=σ2 ​=N∑(x−μ)2​ ​=s2 ​=n−1∑(x−xˉ)2​ ​​


如何找到均值 ($\mu$)?

这是公式:

μ = ∑ x N x ˉ = ∑ x n \begin{aligned} \mu = \frac{\sum{x}}{N} \\ \bar{x} = \frac{\sum{x}}{n} \end{aligned} μ=N∑x​xˉ=n∑x​​


符号

符号回顾:

总体样本描述
σ 2 \sigma^2 σ2 s 2 s^2 s2方差
σ \sigma σ s s s标准差
μ \mu μ x ˉ \bar{x} xˉ均值
N N N n n n项的总和
x − μ x - \mu x−μ x − x ˉ x - \bar{x} x−xˉ偏差
∑ ( x − μ ) 2 \sum{(x - \mu)^2} ∑(x−μ)2 ∑ ( x − x ˉ ) 2 \sum{(x - \bar{x})^2} ∑(x−xˉ)2平方和

关于偏度:

根据经验法则: 如果偏度小于$-1$或大于$1$，分布是高度偏斜的。如果偏度在$-1$和$-0.5$之间或在$0.5$和$1$之间，分布是中度偏斜的。如果偏度在$-0.5$和$0.5$之间，分布近似对称。


关于峰度:

对于峰度，一般准则是如果数字大于$+1$，分布太尖峭。同样，峰度小于$-1$表示分布太平坦。偏度和/或峰度超过这些准则的分布被认为是非正态的。

5.2.1 | 数值列 

# 定义一个函数 numerical_plotting，用于绘制数值型数据的分布图
# 参数 data：要绘制的数据集
# 参数 col：要绘制的数据列名
# 参数 title：图表的标题
# 参数 symb：数据点的形状
# 参数 ylabel：y轴的标签
# 参数 color：数据点的颜色
numerical_plotting(data=loan, col="income", 
                   title="Customer Income Distribution", 
                   symb=" ", ylabel="Density", color="red");

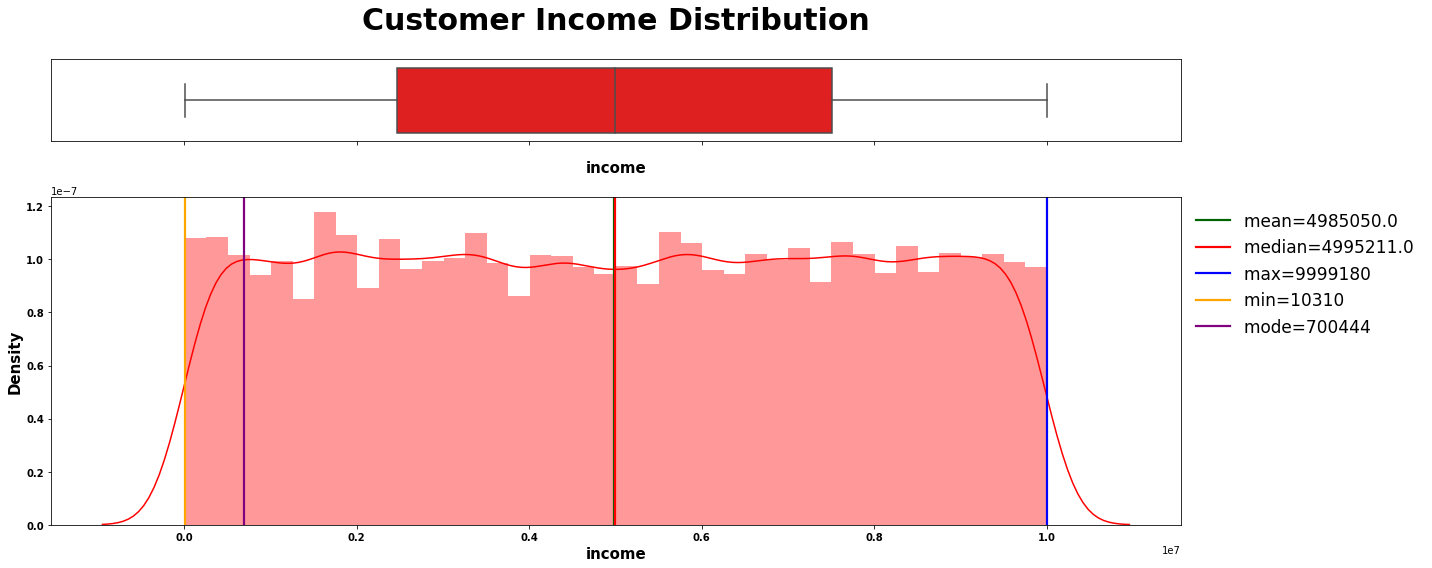
5.2.1.1 | 注释： 
# 使用Chebychev不等式绘制图表
chebychev(loan.income, title="Income", interpret=f"at least 75% customer income is lies between 0 and 10.785.254 Rupee")

-------------------- Interpretation of Income --------------------
first calc: -804582.6
second calc: 10774682.6
at least 75% customer income is lies between 0 and 10.785.254 Rupee
----------------------------------------

skew_kurtosis(loan.income, "Skew & Kurtosis Income")

-------------------- Skew & Kurtosis Income --------------------
Skewness: 3.263568335882554e-05
Approximately symmetric
-----------------------------------
Kurtosis: -1.2113073394580804
The distribution is too flat
-----------------------------------


# 调用numerical_plotting函数，传入参数：数据集loan、要绘制的列age、图表标题Customer Age Distribution、分隔符" "、坐标轴标签Density、颜色salmon
numerical_plotting(data=loan, col="age", 
                   title="Customer Age Distribution", 
                   symb=" ", ylabel="Density", color="salmon");

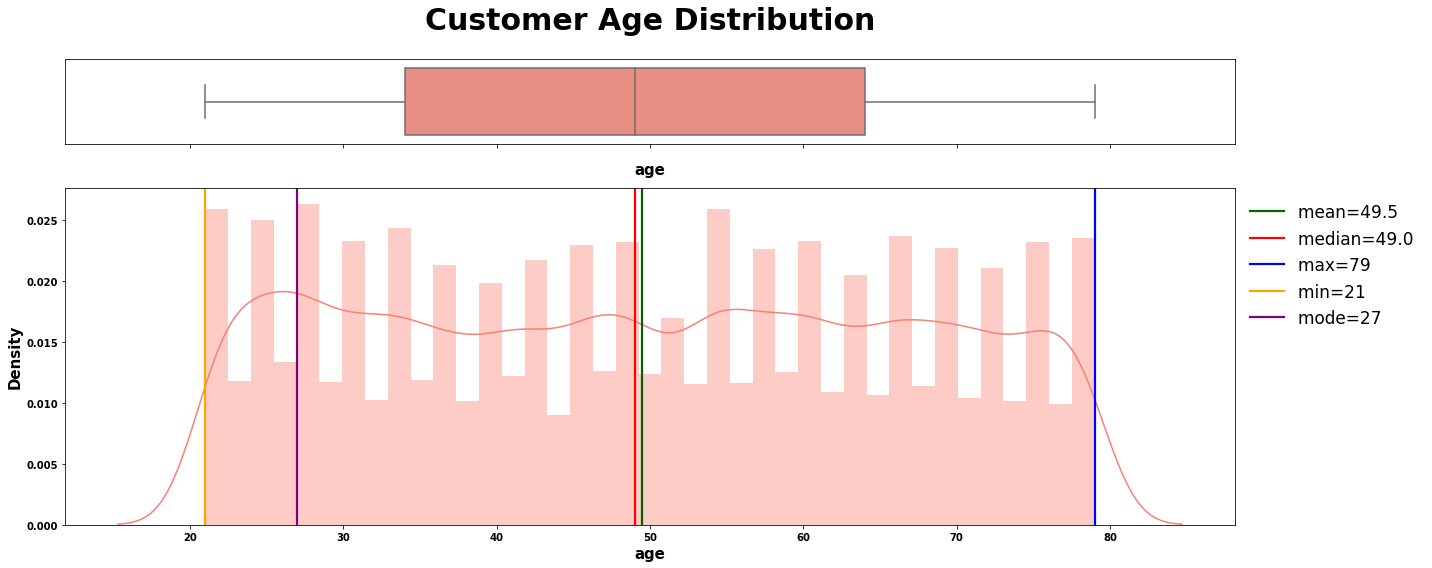
5.2.1.2 | 注释： 
# 使用Chebychev不等式对贷款数据集中的年龄数据进行分析
chebychev(loan.age, title="Age", 
          interpret=f"at least 75% customer age is lies between 0 and 84") 
# 将分析结果以图表形式展示，并添加标题"Age"
# 根据Chebychev不等式，至少有75%的客户的年龄在0到84岁之间，将这一结论添加为文本解释

-------------------- Interpretation of Age --------------------
first calc: 15.1
second calc: 83.9
at least 75% customer age is lies between 0 and 84
----------------------------------------


# 调用函数，计算年龄的偏度和峰度
skew_kurtosis(data.age, "Skew & Kurtosis Age")

-------------------- Skew & Kurtosis Age --------------------
Skewness: 0.02146490933734407
Approximately symmetric
-----------------------------------
Kurtosis: -1.2184017787346195
The distribution is too flat
-----------------------------------

# 定义一个函数 numerical_plotting，用于绘制数值型数据的分布图
# 参数说明：
# - data: 数据集，这里传入的是名为loan的数据集
# - col: 要绘制分布图的列名，这里传入的是"experience"
# - title: 图表的标题，这里传入的是"Customer Experience Distribution"
# - symb: 分布图中的符号，这里传入的是空格" "
# - ylabel: y轴的标签，这里传入的是"Density"
# - color: 图表的颜色，这里传入的是"gray"

numerical_plotting(data=loan, col="experience", 
                   title="Customer Experience Distribution", 
                   symb=" ", ylabel="Density", color="gray");

5.2.1.3 | 注释： 
# 使用Chebychev不等式计算贷款经验的统计信息
# 参数loan.experience表示贷款申请者的工作经验
# 参数title表示图表的标题
# 参数interpret表示解释图表的含义，即至少75%的客户在0到22年的工作经验范围内。
chebychev(loan.experience, title="Experience", 
          interpret=f"at least 75% customer have 0 to 22 years professional experience of working")

-------------------- Interpretation of Experience --------------------
first calc: -2.2
second calc: 21.8
at least 75% customer have 0 to 22 years professional experience of working
----------------------------------------

# 调用函数计算经验数据的偏度和峰度
skew_kurtosis(loan.experience, "Skew & Kurtosis Experience")

-------------------- Skew & Kurtosis Experience --------------------
Skewness: 0.02497250061102099
Approximately symmetric
-----------------------------------
Kurtosis: -1.2150902092155016
The distribution is too flat
-----------------------------------

# 定义一个函数 numerical_plotting，用于绘制数值型数据的分布图
# 参数data表示数据集，col表示要绘制的列名，title表示图表的标题，symb表示分隔符，ylabel表示y轴的标签，color表示图表的颜色
numerical_plotting(data=loan, col="current_job_yrs", 
                   title="Customer Current Job Years Distribution", 
                   symb=" ", ylabel="Density", color="gold");

5.2.1.4 | 注释： 
# 使用chebychev函数计算给定数据的切比雪夫距离
chebychev(loan.current_job_yrs, title="Current Job Years", interpret=f"at least 75% customer have 0 to 13 years of work experience in current job")

-------------------- Interpretation of Current Job Years --------------------
first calc: -1.1
second calc: 13.7
at least 75% customer have 0 to 13 years of work experience in current job
----------------------------------------

# 调用函数计算偏度和峰度
skew_kurtosis(loan.current_job_yrs, "Skew & Kurtosis Current Job Years")

-------------------- Skew & Kurtosis Current Job Years --------------------
Skewness: 0.283080184869882
Approximately symmetric
-----------------------------------
Kurtosis: -0.806885499528117
The distribution is non-normal
-----------------------------------

# 定义一个函数 numerical_plotting，用于绘制数值型数据的分布图
# 参数data表示要绘制的数据集，col表示要绘制的数据列名
# 参数title表示图表的标题，symb表示图表中的分隔符，ylabel表示y轴的标签，color表示图表的颜色
numerical_plotting(data=loan, col="current_house_yrs", 
                   title="Customer Current House Years Distribution", 
                   symb=" ", ylabel="Density", color="blue");

5.2.1.5 | 注释： 
# 使用Chebychev算法计算贷款客户当前居住年限的分布情况
chebychev(loan.current_house_yrs, 
          title="Current House Years", 
          interpret=f"at least 75% customer have lived 9 to 15 years in the current residence") 

# 参数说明：
# loan.current_house_yrs：贷款客户当前居住年限的数据
# title：图表标题
# interpret：对分布情况的解释，至少75%的客户在当前住所居住了9到15年。

-------------------- Interpretation of Current House Years --------------------
first calc: 9.2
second calc: 14.8
at least 75% customer have lived 9 to 15 years in the current residence
----------------------------------------

# 定义一个名为skew_kurtosis的函数，该函数接受两个参数：数据集和标题
skew_kurtosis(loan.current_house_yrs, "Skew & Kurtosis Current House Years")

-------------------- Skew & Kurtosis Current House Years --------------------
Skewness: 0.011033214792934528
Approximately symmetric
-----------------------------------
Kurtosis: -1.2733173521714056
The distribution is too flat
-----------------------------------

5.2.2 | 分类列 

# 统计贷款数据中婚姻状况的数量
loan_married_single = loan["married_single"].value_counts()

# 绘制饼图和计数图
count_pie_plot(
    datapie=loan_married_single,  # 饼图数据
    datacount=loan,  # 计数图数据
    colcount="married_single",  # 计数图的列名
    colpiey=loan_married_single.values,  # 饼图的y轴数据
    text1="Married or Single",  # 图表标题
    pielabels=["Single", "Married"],  # 饼图标签
    text2="Are you Married or Single?",  # 图表副标题
    piecomap=["#001253", "#FF5858"],  # 饼图颜色
    countcomap=["#001253", "#FF5858"],  # 计数图颜色
    xlabel="Married Single",  # x轴标签
    piefs=15,  # 饼图字体大小
    yplus=5000,  # y轴最大值增量
    ylabel="Count of Observations",  # y轴标签
    xticklabel=["Single", "Married"],  # x轴刻度标签
    yticklabel=list(np.arange(0, 260000, 50000)),  # y轴刻度标签
    ystart=0,  # y轴起始值
    yend=250000  # y轴结束值
);


# 统计贷款数据中不同房屋所有权类型的数量
loan_house_ownership = loan["house_ownership"].value_counts()

# 绘制饼图和计数图
count_pie_plot(
    datapie=loan_house_ownership,  # 饼图数据
    datacount=loan,  # 计数图数据
    colcount="house_ownership",  # 计数图的列名
    colpiey=loan_house_ownership.values,  # 饼图的y轴数据
    text1="House Ownership",  # 图表标题
    pielabels=["Rented", "Owned", "No rent No own"],  # 饼图标签
    text2="What customer house status?",  # 图表副标题
    piecomap=["#E0144C", "#3AB0FF", "#FF5858"],  # 饼图颜色
    countcomap=["#E0144C", "#FF5858", "#3AB0FF"],  # 计数图颜色
    xlabel="Married Single",  # x轴标签
    piefs=10,  # 饼图字体大小
    yplus=5000,  # y轴上限增量
    pctdistance=0.7,  # 饼图标签距离圆心的距离
    ylabel="Count of Observations",  # y轴标签
    xticklabel=["Rented", "No rent No own", "Owned"],  # x轴刻度标签
    yticklabel=list(np.arange(0, 260000, 50000)),  # y轴刻度标签
    ystart=0,  # y轴起始值
    yend=250000  # y轴结束值
)


# 统计贷款数据中不同车辆所有权的数量
loan_car_ownership = loan["car_ownership"].value_counts()

# 绘制饼图和计数图
count_pie_plot(
    datapie=loan_car_ownership,  # 饼图数据
    datacount=loan,  # 计数图数据
    colcount="car_ownership",  # 计数图的列名
    colpiey=loan_car_ownership.values,  # 饼图的y轴数据
    text1="Car Ownership",  # 图表标题
    pielabels=["No", "Yes"],  # 饼图标签
    text2="Does customer owned a car?",  # 图表副标题
    piecomap=["#001253", "#FF5858"],  # 饼图颜色映射
    countcomap=["#001253", "#FF5858"],  # 计数图颜色映射
    xlabel="Car Ownership",  # x轴标签
    piefs=15,  # 饼图字体大小
    yplus=5000,  # y轴上限增量
    ylabel="Count of Observations",  # y轴标签
    xticklabel=["No", "Yes"],  # x轴刻度标签
    yticklabel=list(np.arange(0, 225000, 25000)),  # y轴刻度标签
    ystart=0,  # y轴起始值
    yend=200000  # y轴结束值
)


# 定义函数countplot_y，用于绘制柱状图
# 参数说明：
# data：数据集，表示要绘制柱状图的数据
# coly：字符串，表示数据集中的一个列名，用于指定要绘制柱状图的变量
# sizey：整数，表示柱状图的大小
# xplus：整数，表示x轴刻度的增量
# text1：字符串，表示柱状图的标题
# text2：字符串，表示柱状图的副标题
# xlabel：字符串，表示x轴的标签
# ytimes1：浮点数，表示y轴刻度的倍数
# ytimes2：浮点数，表示y轴刻度的倍数
# xstart：整数，表示x轴刻度的起始值
# xend：整数，表示x轴刻度的结束值

data = loan  # 将变量loan赋值给data，作为数据集
coly = "profession"  # 将字符串"profession"赋值给coly，表示要绘制柱状图的变量
sizey = 50  # 将整数50赋值给sizey，表示柱状图的大小
text1 = "The count observation of each Profession"  # 将字符串"The count observation of each Profession"赋值给text1，表示柱状图的标题
text2 = "Which profession has the most?"  # 将字符串"Which profession has the most?"赋值给text2，表示柱状图的副标题
xlabel = "Count of Observations"  # 将字符串"Count of Observations"赋值给xlabel，表示x轴的标签
ylabel = "Profession"  # 将字符串"Profession"赋值给ylabel，表示y轴的标签
xstart, xend = 0, 5000  # 将整数0赋值给xstart，将整数5000赋值给xend，表示x轴刻度的起始值和结束值
xplus = 100  # 将整数100赋值给xplus，表示x轴刻度的增量
ytimes1, ytimes2 = 3.5, 2  # 将浮点数3.5赋值给ytimes1，将浮点数2赋值给ytimes2，表示y轴刻度的倍数

# 调用函数countplot_y，传入相应的参数进行绘图
countplot_y(data=data, coly=coly, sizey=sizey, xplus=xplus,
            text1=text1, text2=text2, xlabel=xlabel, ytimes1=ytimes1, 
            ytimes2=ytimes2, ylabel=ylabel, xstart=xstart, xend=xend);


# 定义函数countplot_y，用于绘制柱状图
# 参数说明：
# - data: 数据集，表示要绘制柱状图的数据
# - coly: 字符串，表示数据集中的某一列，作为y轴的数据
# - sizey: 整数，表示y轴的长度
# - xplus: 整数，表示x轴刻度之间的间隔
# - text1: 字符串，表示图表的标题
# - text2: 字符串，表示图表的副标题
# - xlabel: 字符串，表示x轴的标签
# - ytimes1: 浮点数，表示y轴刻度之间的间隔
# - ytimes2: 浮点数，表示y轴刻度之间的间隔
# - ylabel: 字符串，表示y轴的标签
# - xstart: 整数，表示x轴的起始值
# - xend: 整数，表示x轴的结束值

# 调用countplot_y函数，传入参数data、coly、sizey、xplus、text1、text2、xlabel、ytimes1、ytimes2、ylabel、xstart、xend，绘制柱状图
data = loan
coly = "city"
sizey = 150
text1 = "The count observation of each City"
text2 = "Which city has the most?"
xlabel = "Count of Observations"
ylabel = "City"
xstart, xend = 0, 600
xplus = 10
ytimes1, ytimes2 = 5.5, 3

countplot_y(data=data, coly=coly, sizey=sizey, xplus=xplus,
            text1=text1, text2=text2, xlabel=xlabel, ytimes1=ytimes1,
            ytimes2=ytimes2, ylabel=ylabel, xstart=xstart, xend=xend);


# 定义函数countplot_y，用于绘制柱状图
# 参数data表示数据集，coly表示要统计的列名，sizey表示图表的大小，xplus表示x轴刻度间隔
# text1表示图表标题，text2表示图表副标题，xlabel表示x轴标签，ylabel表示y轴标签
# xstart和xend表示x轴的起始和结束值，ytimes1和ytimes2表示y轴的缩放倍数
data = loan
coly = "state"
sizey = 15
text1 = "The count observation of each State"
text2 = "Which state has the most?"
xlabel = "Count of Observations"
ylabel = "State"
xstart, xend = 0, 10000
xplus = 200
ytimes1, ytimes2 = 5.5, 3

countplot_y(data=data, coly=coly, sizey=sizey, xplus=xplus,
            text1=text1, text2=text2, xlabel=xlabel, ytimes1=ytimes1,
            ytimes2=ytimes2, ylabel=ylabel, xstart=xstart, xend=xend);

5.3 | 双变量分析

5.3.1 | 什么是相关性？

相关性是一个统计量（表示为一个数字），用于描述两个或多个变量之间的关系的大小和方向。然而，变量之间的相关性并不意味着一个变量的变化自动导致了另一个变量值的变化。

数据集中的变量之间可能有很多原因导致相关性。

例如：

  • 一个变量可能导致或依赖于另一个变量的值。
  • 一个变量可能与另一个变量轻微相关。
  • 两个变量可能依赖于第三个未知变量。

在数据分析和建模中，了解变量之间的关系可以很有用。两个变量之间的统计关系被称为它们的相关性。

相关性可以是正相关，意味着两个变量的变化方向相同，也可以是负相关，意味着当一个变量的值增加时，另一个变量的值减少。相关性也可以是中性或零，意味着变量之间没有关系。

  • 正相关：两个变量的变化方向相同。
  • 中性相关：变量的变化之间没有关系。
  • 负相关：变量的变化方向相反。

如果两个或多个变量之间紧密相关，即存在多重共线性，某些算法的性能可能会下降。一个例子是线性回归，其中应该删除一个有问题的相关变量，以提高模型的准确性。

我们还可能对输入变量与输出变量之间的相关性感兴趣，以便了解哪些变量可能或可能不相关，作为开发模型的输入的见解。

关系的结构可能是已知的，例如线性关系，或者我们可能不知道两个变量之间是否存在关系，以及可能采取的结构。根据关系的已知情况和变量的分布，可以计算不同的相关性分数。

皮尔逊相关系数

r = ∑ ( x i − x ˉ ) ( y i − y ˉ ) ∑ ( x i − x ˉ ) 2 ∑ ( y i − y ˉ ) 2 r = \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2 \sum(y_i - \bar{y})^2}} r=∑(xi​−xˉ)2∑(yi​−yˉ​)2 ​∑(xi​−xˉ)(yi​−yˉ​)​

皮尔逊相关系数（以Karl Pearson命名）可用于总结两个数据样本之间线性关系的强度。

皮尔逊相关系数的计算方法是两个变量的协方差除以每个数据样本的标准差的乘积。它是将两个变量之间的协方差归一化以得到可解释的分数。

皮尔逊相关系数 = 协方差(X, Y) / (标准差(X) * 标准差(Y))

计算中使用均值和标准差表明两个数据样本需要具有高斯或类似高斯的分布。

计算的结果，相关系数可以解释为了解关系。

相关系数返回一个介于 − 1 -1 −1和 1 1 1之间的值，表示从完全负相关到完全正相关的相关性的限制。值为 0 0 0表示没有相关性。必须解释该值，通常值低于 − 0.5 -0.5 −0.5或高于 0.5 0.5 0.5表示显著的相关性，而低于这些值的值则表示较不显著的相关性。

可以使用pearsonr() SciPy函数计算具有相同长度的两个数据样本之间的皮尔逊相关系数。

5.3.1 | 非参数秩相关

相关性是指两个变量的观察值之间的关联。

这些变量可能具有正相关，这意味着随着一个变量的值增加，另一个变量的值也增加。关联也可能是负相关，这意味着随着一个变量的值增加，另一个变量的值减少。最后，关联可能是中性的，这意味着变量之间没有关联。

相关性量化了这种关联，通常作为一个介于 − 1 -1 −1到 1 1 1之间的度量，用于完全负相关和完全正相关。计算得到的相关性被称为“相关系数”。然后可以解释该相关系数以描述这些度量。

请参阅下表以帮助解释相关系数。

表格

直接关系的相关系数间接关系的相关系数变量之间的关系强度
0.0 0.0 0.0 0.0 0.0 0.0无/微小
0.1 0.1 0.1 − 0.1 -0.1 −0.1弱/小
0.3 0.3 0.3 − 0.3 -0.3 −0.3中等/中等
0.5 0.5 0.5 − 0.5 -0.5 −0.5强/大
1.0 1.0 1.0 − 1.0 -1.0 −1.0完美

可以使用标准方法（如皮尔逊相关系数）计算具有高斯分布的两个变量之间的相关性。对于没有高斯分布的数据，不能使用此过程。相反，必须使用秩相关方法。

秩相关是指使用值之间的序数关系而不是具体值来量化变量之间的关联的方法。序数数据是具有标签值并具有顺序或秩关系的数据；例如：‘低’，‘中’和’高’。

秩相关可以计算实值变量的相关性。首先，将每个变量的值转换为秩数据。这是将值排序并分配一个整数秩值的过程。然后可以计算秩相关系数以量化两个秩变量之间的关联。

由于不假设值的分布，秩相关方法被称为无分布相关或非参数相关。有趣的是，秩相关测量通常用作其他统计假设检验的基础，例如确定两个样本是否可能来自相同（或不同）的总体分布。

秩相关方法通常以开发该方法的研究人员的名字命名。秩相关方法的四个示例如下：

  • 斯皮尔曼秩相关。
  • 肯德尔秩相关。
  • 古德曼和克鲁斯卡尔秩相关。
  • 桑默斯秩相关。

在接下来的几节中，我们将更详细地介绍两种较常见的秩相关方法：斯皮尔曼秩相关和

斯皮尔曼秩相关

p = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) p = 1 - \frac{6 \sum d^2_i}{n(n^2 - 1)} p=1−n(n2−1)6∑di2​​

斯皮尔曼秩相关以Charles Spearman命名。

它也可以称为斯皮尔曼相关系数，用小写希腊字母rho（p）表示。因此，它可以称为斯皮尔曼的rho。

这种统计方法通过单调函数（即递增或递减关系）来量化排名变量之间的关联程度。作为统计假设检验，该方法假设样本之间不相关（无法拒绝H0）。

斯皮尔曼秩序相关是一种统计过程，旨在测量在测量的序数尺度上两个变量之间的关系。

— 第124页，非统计学家的非参数统计：一种逐步方法，2009年。

斯皮尔曼秩相关的直觉是，它使用秩值而不是实际值计算皮尔逊相关（例如，相关性的参数测量）。其中皮尔逊相关是计算两个变量之间的协方差（或观测值与均值之间的预期差异）归一化为两个变量的方差或扩展。

可以使用Python中的spearmanr() SciPy函数计算斯皮尔曼秩相关。

5.3.1 | 数值列 



# 调用 pearson_correlation 函数，计算 "income" 和 "risk_flag" 之间的相关性
pearson_correlation(loan["income"], loan["risk_flag"], "Income & Risk Flag Correlation")

--------------- Income & Risk Flag Correlation ---------------

Pearson correlation coefficient: -0.004

Samples are uncorrelated (fail to reject H0) p=0.315

# 调用函数计算年龄和风险标志之间的相关系数
pearson_correlation(loan["age"], loan["risk_flag"], "Age & Risk Flag Correlation")

--------------- Age & Risk Flag Correlation ---------------

Pearson correlation coefficient: -0.030

Samples are correlated (reject H0) p=0.000

# 调用函数计算相关系数并绘制散点图
pearson_correlation(loan["experience"], loan["risk_flag"], "Experience & Risk Flag Correlation")

--------------- Experience & Risk Flag Correlation ---------------

Pearson correlation coefficient: -0.050

Samples are correlated (reject H0) p=0.000


# 调用 pearson_correlation 函数计算 "current_job_yrs" 和 "risk_flag" 之间的相关系数
correlation = pearson_correlation(loan["current_job_yrs"], loan["risk_flag"], "Current Job Years & Risk Flag Correlation")

--------------- Current Job Years & Risk Flag Correlation ---------------

Pearson correlation coefficient: -0.023

Samples are correlated (reject H0) p=0.000



# 调用函数计算"current_house_yrs"和"risk_flag"的相关系数
pearson_correlation(loan["current_house_yrs"], loan["risk_flag"], "Current Job Years & Risk Flag Correlation")

--------------- Current Job Years & Risk Flag Correlation ---------------

Pearson correlation coefficient: -0.008

Samples are correlated (reject H0) p=0.037

5.3.2 | 分类列 

# 调用函数并传入相关参数
spearman_correlation(data1=loan["car_ownership"], data2=loan["risk_flag"], title="Car Ownership & Risk Flag Correlation")

--------------- Car Ownership & Risk Flag Correlation ---------------

Spearmans correlation coefficient: -0.039

Samples are correlated (reject H0) p=0.000

# 调用函数，计算并绘制"Profession"和"Risk Flag"之间的相关性
spearman_correlation(data1=loan["profession"], data2=loan["risk_flag"], title="Profession & Risk Flag Correlation")

--------------- Profession & Risk Flag Correlation ---------------

Spearmans correlation coefficient: -0.005

Samples are uncorrelated (fail to reject H0) p=0.214

# 调用函数，计算并绘制"city"和"risk_flag"之间的Spearman相关系数
spearman_correlation(data1=loan["city"], data2=loan["risk_flag"], title="City & Risk Flag Correlation")

--------------- City & Risk Flag Correlation ---------------

Spearmans correlation coefficient: 0.005

Samples are uncorrelated (fail to reject H0) p=0.201

# 调用函数，计算并绘制"state"和"risk_flag"之间的Spearman相关系数
spearman_correlation(data1=loan["state"], data2=loan["risk_flag"], title="State & Risk Flag Correlation")

--------------- State & Risk Flag Correlation ---------------

Spearmans correlation coefficient: -0.006

Samples are uncorrelated (fail to reject H0) p=0.112

5.4 | 多元分析

5.4.1 | 分类列 

# 从loan数据集中选取职业为"Drafter", "Secretary", "Computer_hardware_engineer", "Analyst", "Official"的数据
I = (loan.loc[loan["profession"].isin(["Drafter", "Secretary", "Computer_hardware_engineer", "Analyst", "Official"])]
     .loc[:, ["income", "profession", "risk_flag"]])

# 将选取的数据赋值给变量data
data = I

# 设置图表的标题为"Top 5 Profession & Risk Flag"
title = "Top 5 Profession & Risk Flag"

# 设置x轴的标签为"profession"
x = "profession"

# 设置y轴的标签为"income"
y = "income"

# 设置颜色分类的标签为"risk_flag"
hue = "risk_flag"

# 设置x轴的标签为"Top 5 Profession Income"
xlabel = "Top 5 Profession Income"

# 设置y轴的标签为"Income"
ylabel = "Income"

# 调用mtvboxplot函数，绘制箱线图
mtvboxplot(data=data, title=title, x=x, y=y, hue=hue, xlabel=xlabel, ylabel=ylabel);


# 从loan数据集中选择城市为"Bhubaneswar", "Bettiah", "Gwalior", "Kavali","Bardhaman"的数据，并且只选择"income", "city", "risk_flag"这三列数据
C = (loan.loc[loan["city"].isin(["Bhubaneswar", "Bettiah", "Gwalior", "Kavali","Bardhaman"])].loc[:, ["income", "city", "risk_flag"]])

# 将C赋值给data变量
data = C

# 设置图表的标题为"Top 5 City & Risk Flag"
title = "Top 5 City & Risk Flag"

# 设置x轴的标签为"city"
x = "city"

# 设置y轴的标签为"income"
y = "income"

# 设置颜色标记的变量为"risk_flag"
hue = "risk_flag"

# 设置x轴的标签为"Top 5 City Income"
xlabel = "Top 5 City Income"

# 设置y轴的标签为"Income"
ylabel = "Income"

# 调用mtvboxplot函数，传入data、title、x、y、hue、xlabel、ylabel这些参数，并生成图表
mtvboxplot(data=data, title=title, x=x, y=y, hue=hue, xlabel=xlabel, ylabel=ylabel);




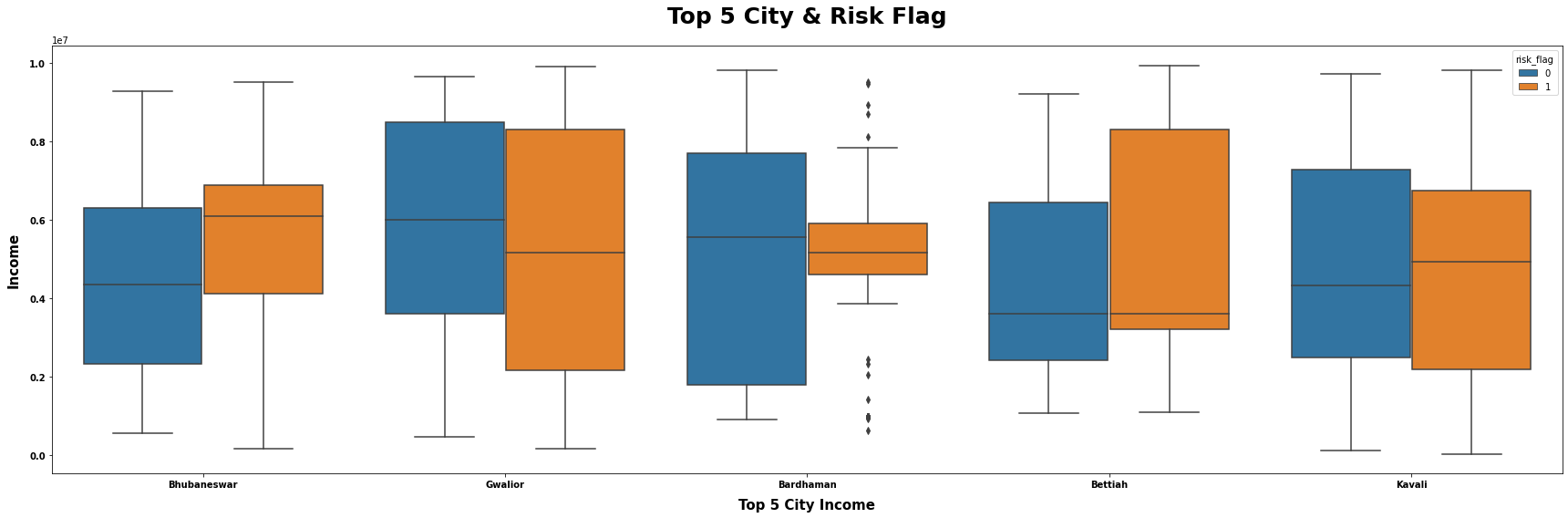
# 定义数据集S为满足条件的loan数据集中的特定列
S = (loan.loc[loan["state"].isin(["Manipur", "Kerala", "Tripura", "Madhya", "Jammu"])].loc[:, ["income", "state", "risk_flag"]])

# 定义图表的标题
title = "Top 5 State & Risk Flag"

# 定义x轴的数据列
x = "state"

# 定义y轴的数据列
y = "income"

# 定义用于分组的数据列
hue = "risk_flag"

# 定义x轴的标签
xlabel = "Top 5 State Income"

# 定义y轴的标签
ylabel = "Income"

# 调用mtvboxplot函数，传入数据和相关参数，生成箱线图
mtvboxplot(data=data, title=title, x=x, y=y, hue=hue, xlabel=xlabel, ylabel=ylabel);




# 从数据集中筛选出house_ownership为"rented"、"owned"或"norent_noown"的行，并选择income、house_ownership和risk_flag三列
H = (data.loc[data["house_ownership"].isin(["rented", "owned", "norent_noown"])].loc[:, ["income", "house_ownership", "risk_flag"]])

# 将筛选后的数据集赋值给变量data
data = H

# 将图表的标题赋值给变量title
title = "House Ownership & Risk Flag"

# 将x轴的数据列名赋值给变量x
x = "house_ownership"

# 将y轴的数据列名赋值给变量y
y = "income"

# 将用于分组的数据列名赋值给变量hue
hue = "risk_flag"

# 将x轴的标签赋值给变量xlabel
xlabel = "House Ownership"

# 将y轴的标签赋值给变量ylabel
ylabel = "Income"

# 调用mtvboxplot函数，传入参数data、title、x、y、hue、xlabel和ylabel，绘制箱线图
mtvboxplot(data=data, title=title, x=x, y=y, hue=hue, xlabel=xlabel, ylabel=ylabel)



# 从数据集中筛选出符合条件的数据
M = (loan.loc[loan["married_single"].isin(["single", "married"])].loc[:, ["income", "married_single", "risk_flag"]])

# 将筛选出的数据赋值给变量data
data = M

# 设置图表的标题
title = "Married Single & Risk Flag"

# 设置x轴的数据列名
x = "married_single"

# 设置y轴的数据列名
y = "income"

# 根据该列数据进行分组，不同组的箱线图以不同颜色表示
hue = "risk_flag"

# 设置x轴的标签
xlabel = "Married Single"

# 设置y轴的标签
ylabel = "Income"

mtvboxplot(data=data, title=title, x=x, y=y, 
           hue=hue, xlabel=xlabel, ylabel=ylabel)


# 从loan数据集中选取car_ownership列的值为"no"或"single"的行，并选取income、car_ownership和risk_flag这三列作为新的数据集CO
CO = (loan.loc[loan["car_ownership"].isin(["no", "single"])].loc[:, ["income", "car_ownership", "risk_flag"]])

# 将CO数据集赋值给变量data
data = CO

# 设置标题为"Car Ownership & Risk Flag"
title = "Car Ownership & Risk Flag"

# 设置x轴的变量为"car_ownership"
x = "car_ownership"

# 设置y轴的变量为"income"
y = "income"

# 设置颜色变量为"risk_flag"
hue = "risk_flag"

# 设置x轴的标签为"Car Ownership"
xlabel = "Car Ownership"

# 设置y轴的标签为"Income"
ylabel = "Income"

# 调用mtvboxplot函数，传入data、title、x、y、hue、xlabel和ylabel作为参数，绘制箱线图
mtvboxplot(data=data, title=title, x=x, y=y, hue=hue, xlabel=xlabel, ylabel=ylabel);

5.4.2 | 数值列 

# 创建相关性矩阵
corr = loan.corr()

# 生成上三角形的掩码；True表示不显示
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True

# 设置matplotlib图形
fig, ax = plt.subplots(figsize=(11, 9))

# 生成自定义的发散调色板
cmap = sns.diverging_palette(220, 10, as_cmap=True)

# 使用掩码和正确的纵横比绘制热力图
sns.heatmap(corr,
            mask=mask,
            cmap=cmap,
            annot=True,
            vmax=.3,
            vmin=-.3,
            center=0,
            square=True,
            linewidths=.5,
            cbar_kws={"shrink": .5});



# 将相关系数矩阵以热力图的形式展示，并使用颜色映射进行着色
corr.style.background_gradient(cmap=cmap)
 incomeageexperiencecurrent_job_yrscurrent_house_yrsrisk_flag
income1.0000000.006296-0.0023160.001214-0.001418-0.004039
age0.0062961.000000-0.0029800.019246-0.014451-0.029516
experience-0.002316-0.0029801.0000000.6693290.018192-0.050008
current_job_yrs0.0012140.0192460.6693291.0000000.003180-0.022537
current_house_yrs-0.001418-0.0144510.0181920.0031801.000000-0.008364
risk_flag-0.004039-0.029516-0.050008-0.022537-0.0083641.000000

6 | 数据预处理

6.1 | 获取互信息 

# 导入所需的库
from sklearn.feature_selection import mutual_info_classif
from sklearn.preprocessing import LabelEncoder

# 定义具有Object类型的列以实现LabelEncoder
list_object = loan.select_dtypes("object").columns.tolist()  # 获取数据集中Object类型的列，并转换为列表
encoder = LabelEncoder()  # 创建LabelEncoder对象

# 对每一列进行LabelEncoder编码
for col in list_object:
    loan[col] = encoder.fit_transform(loan[col].values.tolist())  # 将每一列的值转换为列表形式，并使用LabelEncoder进行编码

# 计算数据的互信息

# 将loan数据转换为int64类型，并复制为X_mutual
X_mutual = loan.astype("int64").reset_index().copy()

# 将risk_flag列提取出来作为y_mutual
y_mutual = X_mutual.pop("risk_flag")

# 删除X_mutual中的Id列
del X_mutual["Id"]

# 确定所有离散特征的数据类型为整数
discrete_features = X_mutual.dtypes == int

# 定义计算互信息得分的函数
def make_mi_scores(X_mutual, y_mutual, discrete_features):
    # 使用mutual_info_classif函数计算互信息得分
    mi_scores = mutual_info_classif(X_mutual, y_mutual, discrete_features=discrete_features)
    # 将得分转换为Series类型，并设置名称为"MI Scores"，索引为X_mutual的列名
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X_mutual.columns)
    # 按降序对得分进行排序
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

# 调用make_mi_scores函数计算互信息得分
mi_scores = make_mi_scores(X_mutual, y_mutual, discrete_features)

# 将得分转换为DataFrame类型并输出
mi_scores.to_frame()
MI Scores
income0.570
city0.025
experience0.004
age0.004
state0.003
profession0.003
current_job_yrs0.002
house_ownership0.001
car_ownership0.001
married_single0.001
current_house_yrs0.000
# 变量
scores = mi_scores.sort_values(ascending=True)  # 对互信息得分进行升序排序
width = np.arange(len(scores))  # 创建一个与scores长度相同的数组，用于绘制水平条形图
ticks = list(scores.index)  # 将scores的索引转换为列表，用于设置y轴刻度标签

# 绘图
plt.figure(figsize=(15, 5))  # 创建一个大小为15x5的图像
plt.barh(width, scores, color="salmon", alpha=0.7, edgecolor="k")  # 绘制水平条形图，设置颜色为salmon，透明度为0.7，边缘颜色为黑色
plt.yticks(width, ticks, weight="bold")  # 设置y轴刻度标签为ticks，并设置字体加粗
plt.xticks(weight="bold")  # 设置x轴刻度标签字体加粗
plt.title("Mutual Information Scores",  # 设置标题为"Mutual Information Scores"
          weight="bold",  # 设置标题字体加粗
          fontsize=20,  # 设置标题字体大小为20
          pad=25)  # 设置标题与图像顶部的距离为25个像素

6.2 | 特征选择 

# 定义特征列表，包括"income", "city", "experience", "age", "state", "profession", "current_job_yrs"
features = ["income", "city", "experience", "age", "state", "profession", "current_job_yrs"]

# 从loan数据集中提取特征列
X_features = loan[features]

# 从loan数据集中提取目标列
y_labels = loan["risk_flag"]

# 输出特征列和目标列的形状
print(X_features.shape, y_labels.shape)

((61992, 7), (61992,))

# 查看数据集的前几行
X_features.head()
incomecityexperienceagestateprofessioncurrent_job_yrs
Id
237477360172229737104
1867286000177921707281
95578977416018192414339
249011164979510052925363
104241067512212323271
# 统计y_labels中每个元素的个数，并按照个数从大到小进行排序
y_labels.value_counts()

0    30996
1    30996
Name: risk_flag, dtype: int64

6.3 | 分割数据集 

# 导入train_test_split函数
from sklearn.model_selection import train_test_split

# 使用train_test_split函数将数据集划分为训练集和测试集
# X_features为特征数据，y_labels为标签数据
# random_state为随机种子，保证每次划分结果一致
# test_size为测试集的比例，这里设置为0.25，即25%的数据作为测试集
# stratify参数用于保持训练集和测试集中各类别样本的比例与原始数据集中相同
X_train, X_test, y_train, y_test = train_test_split(
    X_features, y_labels, random_state=42, 
    test_size=.25, stratify=y_labels
)

# 打印训练集和测试集的形状
print(f"X_train shape: {X_train.shape} \n"
       f"X_test shape: {X_test.shape} \n"
       f"y_train shape: {y_train.shape} \n"
       f"y_test.shape: {y_test.shape}")

X_train shape: (46494, 7) 
X_test shape: (15498, 7) 
y_train shape: (46494,) 
y_test.shape: (15498,)

7 | 建模、评分和评估 

# 导入所需的库
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import RandomizedSearchCV

# 定义参数
parameter = {
    "max_depth": [int(x) for x in np.linspace(2, 24, 2)],  # 决策树的最大深度
    "min_samples_split" : [2, 5, 10],  # 分裂内部节点所需的最小样本数
    "min_samples_leaf"  : [1, 2, 4],  # 叶子节点所需的最小样本数
    "max_features": ["auto", "sqrt", "log2"],  # 寻找最佳分割时考虑的特征数
    "criterion": ["gini", "entropy", "log_loss"],  # 衡量分割质量的度量标准
    "splitter": ["best", "random"]  # 选择分割特征的策略
}

# 创建模型
model = RandomizedSearchCV(DecisionTreeClassifier(random_state=42), 
                           param_distributions=parameter, cv=3, n_jobs=-1, verbose=1)
# 使用训练数据拟合模型
model.fit(X_train, y_train)

# 打印模型的训练得分、测试得分和最佳得分
print(f"model train score: {model.score(X_train, y_train)},\n" 
      f"model test score: {model.score(X_test, y_test)},\n" 
      f"model best score: {model.best_score_}")

Fitting 3 folds for each of 10 candidates, totalling 30 fits





RandomizedSearchCV(cv=3, estimator=DecisionTreeClassifier(random_state=42),
                   n_jobs=-1,
                   param_distributions={'criterion': ['gini', 'entropy',
                                                      'log_loss'],
                                        'max_depth': [2, 24],
                                        'max_features': ['auto', 'sqrt',
                                                         'log2'],
                                        'min_samples_leaf': [1, 2, 4],
                                        'min_samples_split': [2, 5, 10],
                                        'splitter': ['best', 'random']},
                   verbose=1)



model train score: 0.8788445820966146,
model test score: 0.8158472060911085,
model best score: 0.816492450638792

# 该代码是在训练模型后，获取模型的最佳参数的代码。
model.best_params_

{'splitter': 'best',
 'min_samples_split': 2,
 'min_samples_leaf': 2,
 'max_features': 'log2',
 'max_depth': 24,
 'criterion': 'entropy'}

# 将最佳模型赋值给变量best_model
best_model = model.best_estimator_

# 使用训练数据X_train和标签y_train对最佳模型进行训练
best_model.fit(X_train, y_train)

DecisionTreeClassifier(criterion='entropy', max_depth=24, max_features='log2',
                       min_samples_leaf=2, random_state=42)

# 导入classification_report函数
from sklearn.metrics import classification_report

# 使用best_model对X_test进行预测，得到预测结果y_pred
y_pred = best_model.predict(X_test)

# 打印预测结果y_pred和真实结果y_test的分类报告
print(classification_report(y_pred, y_test))

              precision    recall  f1-score   support

           0       0.78      0.84      0.81      7121
           1       0.86      0.79      0.82      8377

    accuracy                           0.82     15498
   macro avg       0.82      0.82      0.82     15498
weighted avg       0.82      0.82      0.82     15498
CatBoost算法模型实现贷款违约预测
master_hunter的博客
10-17 1387
此篇文章为整个Boost(提升方法)集成算法模型的终章，前几篇文章依次结合详细项目案例讲解了共四个常用的集成算法模型，每一篇文章都包含实战项目以及可运行代码。仅通过看一遍文章不去实践是很难掌握集成算法模型的，其中很多思想和优化参数的方法需要长期使用才能掌握，集成学习的方法在全球各大机器学习、数据挖掘竞赛中使用的非常广泛，其概念和思想也是风靡学术界和工业界，所以有此需求的朋友推荐细读实践。之前我们已经详细描述了AdaBoost算法模型和GBDT原理以及实践。
大数据分析案例-基于XGBoost算法构建贷款违约预测模型
m0_64336780的博客
07-10 1万+
本项目旨在分析以往用户贷款违约数据集，来分析违约用户的特征，找出影响违约的因素，最后使用机器学习算法构建贷款违约模型，帮助企业更好地管理贷款风险，提高贷款的准确性和效率。本次实验我们分析了贷款违约数据，找出了影响违约最大的因素，最后我们选择使用xgboost模型来构建贷款违约预测模型，模型的准确率为0.88，模型效果还不错，但也有待提高。心得与体会：通过这次Python项目实战，我学到了许多新的知识，这是一个让我把书本上的理论知识运用于实践中的好机会。
35. 贷款违约预测
weixin_46036019的博客
03-07 1793
一、项目介绍 背景 以金融风控中的个人信贷为背景，根据贷款申请人的数据信息预测其是否有违约的可能，以此判断是否通过此项贷款，这是一个典型的分类问题。 具体的列名含义 id 为贷款清单分配的唯一信用证标识 loanAmnt 贷款金额 term 贷款期限（year） interestRate 贷款利率 installment 分期付款金额 grade 贷款等级
金融风控-贷款违约预测
weixin_43869610的博客
09-14 4655
**摘要：**赛题以金融风控中的个人信贷为背景，要求选手根据贷款申请人的数据信息预测其是否有违约的可能，以此判断是否通过此项贷款，这是一个典型的分类问题。赛题以预测用户贷款是否违约为任务，数据集报名后可见并可下载，该数据来自某信贷平台的贷款记录，总数据量超过120w，包含47列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取80万条作为训练集，20万条作为测试集A，20万条作为测试集B，同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。比赛
「机器学习」天池比赛：金融风控贷款违约预测
热门推荐
积一时之步，臻千里之遥程
03-29 2万+
https://zhuanlan.zhihu.com/p/255105477 https://tianchi.aliyun.com/notebook-ai/detail?spm=5176.12586969.1002.18.3b3022faqoVnOw&postId=129318 https://www.jianshu.com/u/63b7115ac4ee https://blog.csdn.net/qq_43401035/category_10383961.html 比赛地址：https://tia
【数据挖掘】项目实战金融风控之贷款违约预测
Fanjufei的博客
06-07 1257
以上是贷款违约预测中常用的方法和技巧，需要根据实际问题和数据的特点来选择合适的方法，并不断优化模型以提高预测精度。以上代码只是一个简单的示例，实际项目中还需要根据实际问题和数据的特点进行更加严谨和全面的处理。贷款违约预测是金融风控中的一个重要问题，下面我将介绍一些常用的贷款违约预测方法和技巧。以下是一个简单的贷款违约预测的代码实现示例，使用逻辑回归模型。1**. 数据清洗**
基于Python的贷款违约预测机器学习实践设计源码
最新发布
10-03
train_use_rfc.py、train_use_dtc.py、train_use_boosting.py等文件则分别对应于使用不同的机器学习算法对模型进行训练，包括随机森林、决策树和梯度提升等模型。每种算法的训练结果和性能评估也有所不同，通过比较...
机器学习-贷款违约行为预测（基于逻辑回归和朴素贝叶斯和随机森林及SVM四种方法实现，资源包含完成则代码及数据，数据3万余条记录
06-07
在本项目中，我们将探讨如何运用机器学习技术来预测贷款违约行为。主要涉及的方法有逻辑回归、朴素贝叶斯、随机森林以及支持向量机。这些算法都是在预测建模中常用的工具，尤其在金融风险评估领域。我们将逐一介绍这...
two-layer-model:复现双层贷款违约风险预测模型
04-19
3. 模型实现：可能包括两个层次的模型，如基于宏观经济因素的第一层模型（如逻辑回归、决策树或随机森林）和基于个体信息的第二层模型（如支持向量机、神经网络）。 4. 训练与验证：使用交叉验证等方法进行模型训练...
零基础入门金融风控 Task2 数据分析
Rock_y的博客
09-16 1066
文章目录1 导入数据分析及可视化过程需要的库2 读取文件3 总体了解4 查看数据集中特征缺失值，唯一值等总结：5 查看特征的数值类型有哪些，对象类型有哪些总结：6 变量分布可视化根据y值不同可视化x某个特征的分布6 时间格式数据处理及查看7 掌握透视图可以让我们更好的了解数据8 用pandas_profiling生成数据报告总结 此部分为零基础入门金融风控的 Task2 数据分析部分，带你来了解数据，熟悉数据，为后续的特征工程做准备，欢迎大家后续多多交流。 赛题：零基础入门数据挖掘 - 零基础入门金融风控之
零基础入门金融风控-贷款违约预测_Task2
duxiaodong1122的博客
09-18 590
贷款违约预测_Task2 本文结合数据分析，给出了本次比赛的基线方案，该基线方案线上评测得分为0.7391。
【机器学习实验】利用逻辑回归预测贷款违约行为Python实现
qbx的博客
04-04 3882
贷款违约预测是现代金融机构信用风险管理的基础。金融机构审批贷款时回收机客户的个人信息，包括年龄、收入、学历、职业、家庭情况和借贷历史等，在对各项信息综合考虑的基础上决定是否审批贷款。为了避免贷款违约，金融机构在对借贷人发放贷款的时候进行评估打分，预测贷款违约的概率，并做出是否发放贷款的判断。本案例利用逻辑回归模型预测贷款人是否会发生违约行为。通过贷款数据（包括个人信息、财务状况和贷款状态等）来训练模型，通过模型分析贷款人的偿还能力，预测贷款申请人是否会发生违约。
机器学习---贷款违约行为预警预测
qq475225253的博客
06-05 1524
人们总是希望看到的现象主要是由少数的关键特征造成的，找到这些关键特征也是数据分析的目的。对变量WORK_PROVINCE进行空值处理后，发现该变量的值比较多，这将导致对该变量独热编码时，产生大量的二元特征，且非常稀疏，因此将其进行维规约，将城市变量规约到省份变量中，最终得到近30个代表省份的虚拟变量。针对标称变量IS_LOCAL、WORK_PROVINCE、MARRY_STATUS，进行独热编码，生成该变量每一个类别对应的虚拟变量，同时需要注意虚拟变量陷阱，剔除作为对照组的虚拟变量，以防止多重共线性。
零基础入门金融风控 Task4 建模与调参
Rock_y的博客
09-24 1458
文章目录Task4 建模与调参4.1 学习目标4.2 内容介绍4.3 模型相关原理介绍4.3.1 逻辑回归模型4.3.2 决策树模型4.3.3 GBDT模型4.3.4 XGBoost模型4.3.5 LightGBM模型4.3.6 Catboost模型4.3.7 时间序列模型(选学)4.3.8 推荐教材：4.4 模型对比与性能评估4.4.1 逻辑回归4.4.2 决策树模型4.4.3 集成模型集成方法（ensemble method）4.4.4 模型评估方法4.4.5 模型评价标准4.5 代码示例4.5.1 导
贷款违约预测---Task1
ZZYYhzhy的博客
09-15 252
分类算法常见的评估指标 一、混淆矩阵 混淆矩阵多用于判断分类器（Classifier）的优劣，适用于分类型的数据模型，如分类树（Classification Tree）、逻辑回归（Logistic Regression）、线性判别分析（Linear Discriminant Analysis）等方法。 （1）若一个实例是正类，并且被预测为正类，即为真正类TP(True Positive ) （2）若一个实例是正类，但是被预测为负类，即为假负类FN(False Negative ) （3）若
数据挖掘实战：个人信贷违约预测
lsxxx2011的专栏
05-21 2559
大家好，我是东哥。本次分享一个数据挖掘实战项目：个人信贷违约预测，此项目对于想要学习信贷风控模型的同学非常有帮助，数据和源码在文末。项目背景当今社会，个人信贷业务发展迅速，但同时也会暴露较...
贷款违约预测学习笔记
submarineas的博客
09-13 4707
赛题介绍 链接：https://tianchi.aliyun.com/competition/entrance/531830/information 赛题数据 赛题以预测用户贷款是否违约为任务，数据集报名后可见并可下载，该数据来自某信贷平台的贷款记录，总数据量超过120w，包含47列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取80万条作为训练集，20万条作为测试集A，20万条作为测试集B，同时会对employmentTitle、purpose、postCode和title等信息进行脱敏
银行案例分析：违约概率预测技术研究
这些模型可能包括逻辑回归、决策树、随机森林、神经网络等机器学习技术。通过分析历史数据，银行可以预测特定条件下借款人的违约概率，进而做出贷款决策，设定利率，以及采取风险缓解措施。 ### 标签：“银行案例_...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

数智笔记

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值