Learning a Decision Tree Algorithm with Transformers 使用Transformer学习决策树算法
论文:https://arxiv.org/abs/2402.03774
代码: https://github.com/EvanZhuang/MetaTree
摘要
决策树以其可解释性和高预测性能而闻名,尤其在表格数据上。传统上,决策树是通过递归算法构建的,在树的每个节点上对数据进行分割。然而,确定最佳分割是具有挑战性的,因为针对局部段优化的决策树可能无法带来全局泛化。为了解决这个问题,我们引入了MetaTree,它通过对经典算法的输出进行过滤来训练基于Transformer的模型,以生成强大的分类决策树。具体而言,我们在大量数据集上拟合贪婪决策树和优化决策树。然后,我们训练MetaTree生成达到强大泛化性能的决策树。这种训练使得MetaTree不仅能够模拟这些算法,还能根据上下文智能地调整策略,从而实现优越的泛化性能。
引言
Transformer(Vaswani等人,2017)已经证明在以前被认为不可能的任务上能够生成准确的预测(OpenAI,2023;Betker等人,2023),但是它们能否生成模型而不仅仅是预测呢?在这项工作中,我们研究了Transformer是否能够生成一类特定的模型:决策树。我们选择决策树作为研究对象,因为它们是现代机器学习和分层推理的基础构建块。它们提供了可解释性,而现代深度学习模型通常会牺牲这一点,同时在各种实际应用中保持着最先进的性能(Grinsztajn等人,2022)。
传统上,决策树是使用基于贪婪启发式算法(Breiman等人,1984;Quinlan,1986)构建的。为了克服贪婪算法带来的偏见,最近的工作提出了优化的离散优化方法来拟合决策树(Lin等人,2020;Hu等人,2019;Bertsimas和Dunn,2017)。然而,完整的决策树优化任务是NP难的(Laurent和Rivest,1976),因此在具有大树深度的情况下计算最优树是不可行的。虽然这些方法在表格上的应用效果很好,但是它们的非可微性带来了集成到深度学习模型中的困难。

图1:MetaTree在真实数据集上展现出强大的泛化能力。MetaTree对于深度为2的树(A)和深度为3的树(B)在91个保留数据集上都具有良好的泛化能力,尽管它只被训练用于生成深度为2的树。MetaTree还对13个Tree-of-prompts数据集具有良好的泛化能力,这些数据集需要构建一棵树来引导大型语言模型(Morris等人,2023)。每个图显示了树集合的平均测试准确率,集合大小为{1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100},误差线表示标准差。
在这项工作中,我们引入了MetaTree,这是一个Transformer模型,旨在根据表格数据集构建决策树。MetaTree递归地应用Transformer来决定每个决策节点的分割特征和值(图2a)。

图2:决策树的创建(a)涉及递归的MetaTree调用。MetaTree仅评估当前状态进行决策。图2b显示了MetaTree的表格注意机制,其中在每个层次上使用行和列注意力处理表格输入,并输出一个表示分割特征j和阈值X_(i,j)的one-hot掩码。
我们训练MetaTree在新数据集上生成高性能的决策树。具体而言,我们在大量数据集上拟合贪婪决策树和优化决策树。然后,我们训练MetaTree生成表现出卓越泛化性能的树。这种训练策略赋予MetaTree独特的优势:它不仅学习模仿这些算法的构建过程,还能根据数据集的特定上下文判断何时倾向于每种算法的方法。这种适应性为传统方法带来了显著的灵活性,传统方法通常局限于单一的算法框架。MetaTree的架构利用了交替的行和列注意机制,以及可学习的绝对位置偏差,用于表格表示。
MetaTree在许多实际数据集上生成高度预测性的树,这些数据集在训练过程中没有见过,始终优于传统的决策树算法(图1)。此外,MetaTree表现出对噪声的鲁棒性,并且可以泛化到涉及高阶交互的问题。进一步的分析显示,MetaTree的性能改进来自于其能够根据数据集的上下文动态切换贪婪或全局方法。最后,偏差-方差分析显示,MetaTree成功地实现了比传统决策树算法更低的经验方差。
相关工作
决策树 有很长一段时间使用贪婪方法来拟合决策树,例如CART(Breiman等人,1984),ID3(Quinlan,1986)或C4.5(Quinlan,2014)。最近的工作通过全局优化克服贪婪启发式算法的偏见,例如使用优化方法拟合决策树(Lin等人,2020;Hu等人,2019;Bertsimas和Dunn,2017);这可以提高性能,但往往会带来极高的计算成本。其他最近的研究通过正则化(Agarwal等人,2022)、迭代更新(Carreira-Perpina´n和Tavallali,2018)或增加灵活性(Tan等人,2022)来改进决策树。
决策树在表格应用中保持着最先进的性能(Grinsztajn等人,2022;Kornblith等人,2022),尤其在随机森林(Breiman,2001)、梯度提升树(Freund等人,1996)和BART(Chipman等人,2010)等集成方法中使用时。一些最近的工作研究了树和Transformer的交叉,例如使用树来引导LLM生成(Morris等人,2023;Yao等人,2023)或者反过来,使用LLM来构建更强大的文本分类决策树(Singh等人,2023)。
学习模型/算法 一些基于学习的方法致力于改进算法,主要是将Transformer与深度强化学习相结合,例如更快的矩阵乘法(Fawzi等人,2022)或更快的排序算法(Mankowitz等人,2023)。一项新的工作研究了使用LLM来迭代生成和改进代码,以发现计算机科学和数学问题的改进解决方案(Romera-Paredes等人,2023)。
其他工作关注于Transformer在上下文中的学习能力。Zhou等人(2023)对长度泛化进行了简单任务探索,并发现Transformer可以轻松泛化到一类问题。一项非常相关的工作研究了Transformer是否能够成功地学习在上下文中生成线性函数、甚至决策树和小型MLP(Garg等人,2022)。尽管取得了这些成功,但最近的研究也发现了Transformer在某些情况下泛化能力的局限性,例如分布偏移(Yadlowsky等人,2023)或算术运算(Dziri等人,2023)。
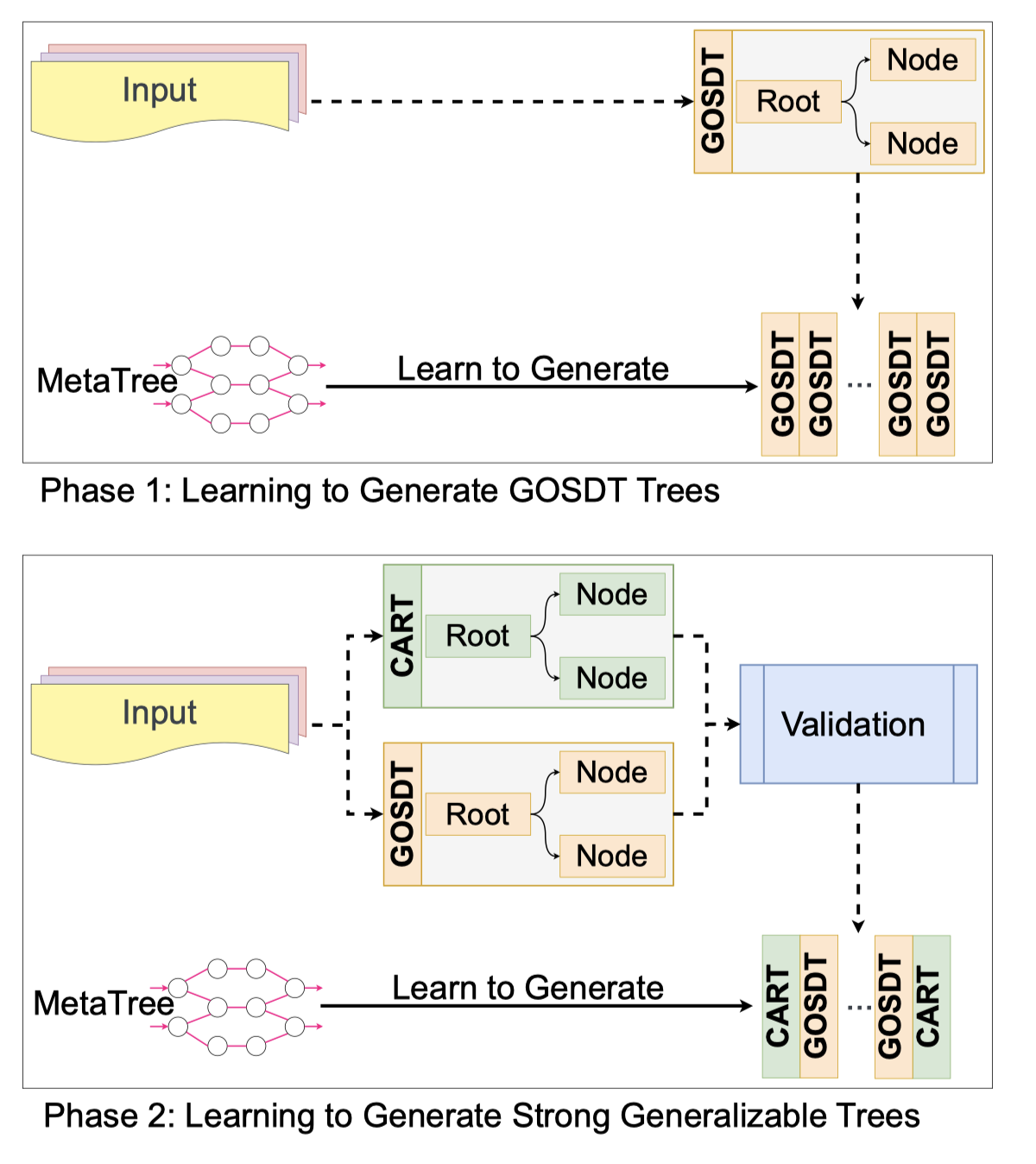
图3:MetaTree的训练包括两个阶段的学习计划:第一阶段专注于从优化的GOSDT树中学习,以尽可能模拟GOSDT算法的行为。然后在第二阶段,训练过程将同时使用GOSDT和CART树的数据,生成具有更好泛化能力的树。
方法:MetaTree
问题定义 在生成决策树时,我们给定一个数据集 D = ( x i , y i ) i = 1 n D=\left(x_{i}, y_{i}\right)_{i=1}^{n} D=(xi,yi)i=1n,其中 x i ∈ R m x_{i} \in \mathbb{R}^{m} xi∈Rm 表示输入特征, y i ∈ { 1 , … , K } y_{i} \in\{1, \ldots, K\} yi∈{1,…,K} 对应每个实例的标签。在每个节点上,决策树通过选择一个特征 j ∈ { 1 , … , m } j \in\{1, \ldots, m\} j∈{1,…,m} 和一个阈值 v ∈ R v \in \mathbb{R} v∈R 来进行分割,使得通过对第 j j j 个特征进行阈值分割,数据集 D D D 可以被分成两个子集。数据集会递归地进行分割,直到达到预先设定的停止准则,例如树的最大深度。为了生成预测,一个数据点会通过树传递,直到到达叶节点,预测的标签是落入该叶节点的训练数据点中占多数的标签。
生成决策树 决策树通常使用自上而下的贪婪算法进行拟合,例如 CART(Breiman 等,1984年)。这些算法在每个节点上贪婪地选择分割,基于一种准则,例如基尼不纯度。尽管这类方法高效,但通常会导致次优解。最近的研究工作研究了“最优”决策树的生成,寻求在最小化树中总分割数的前提下最大化预测性能的解决方案。这可以被形式化为一种树搜索,在搜索节点的所有子节点都被证明为非最优时,对树进行递归修订(Lin 等,2020年)。然而,即使对于较小的树深度,找到最优树也是不可行的,并且很容易过拟合噪声数据。
我们的目标是通过 MetaTree 将这些方法结合起来,生成高度预测性能的决策树,如图2(a)所示。为了生成单棵树,我们在每个树节点上递归调用 MetaTree。最初,整个数据集被呈现给模型,模型通过分割形成根节点。然后,数据集通过根节点被分成两个子集;每个子集(即左子集和右子集)分别通过模型,相反的子集被屏蔽。这个过程重复进行,直到达到树的最大深度。尽管 MetaTree 一次只输出一个分割,但它可以看到整个数据集并使用多个 Transformer 层,使其能够进行自适应、非贪婪的分割。
表示数值输入 MetaTree 接受实值矩阵作为输入。我们使用乘法嵌入将所有数值特征投影到嵌入空间,并将类别嵌入添加到其中。然后,通过一个两层的 MLP 对聚合嵌入进行变换。具体来说,给定一个 n 行 m 列的输入
X
∈
R
n
,
m
X \in \mathbb{R}^{n, m}
X∈Rn,m 和其 k 类标签
Y
∈
{
1
,
…
,
k
}
n
Y \in\{1, \ldots, k\}^{n}
Y∈{1,…,k}n,其中
Y
o
h
Y_{o h}
Yoh 表示
Y
Y
Y 的 one-hot 格式,嵌入计算如下:
Emb
x
(
X
)
=
X
⊗
W
x
∈
R
n
,
m
,
d
,
W
x
∈
R
d
Emb
y
(
Y
)
=
Y
o
h
⋅
W
y
∈
R
n
,
d
,
W
y
∈
R
k
,
d
Emb
=
MLP
(
Emb
x
(
X
)
+
Emb
y
(
Y
)
+
b
1
+
b
2
)
Emb
∈
R
n
,
m
,
d
,
b
1
∈
R
m
,
d
,
b
2
∈
R
n
,
d
\begin{array}{l} \operatorname{Emb}_{\mathbf{x}}(X)=X \otimes W_{x} \in \mathbb{R}^{n, m, d}, \quad W_{x} \in \mathbb{R}^{d} \\ \operatorname{Emb}_{\mathrm{y}}(Y)=Y_{o h} \cdot W_{y} \in \mathbb{R}^{n, d}, \quad W_{y} \in \mathbb{R}^{k, d} \\ \operatorname{Emb}=\operatorname{MLP}\left(\operatorname{Emb}_{\mathrm{x}}(X)+\operatorname{Emb}_{\mathrm{y}}(Y)+b_{1}+b_{2}\right) \\ \operatorname{Emb} \in \mathbb{R}^{n, m, d}, \quad b_{1} \in \mathbb{R}^{m, d}, b_{2} \in \mathbb{R}^{n, d} \end{array}
Embx(X)=X⊗Wx∈Rn,m,d,Wx∈RdEmby(Y)=Yoh⋅Wy∈Rn,d,Wy∈Rk,dEmb=MLP(Embx(X)+Emby(Y)+b1+b2)Emb∈Rn,m,d,b1∈Rm,d,b2∈Rn,d
对于矩阵 X X X 中的每个数字,通过与 W x W_{x} Wx 相乘将其转换为 R d \mathbb{R}^{d} Rd 空间,然后将其添加到 Y Y Y 的类别嵌入中。最终嵌入是通过将聚合嵌入加上位置偏差项 b 1 , b 2 b_{1}, b_{2} b1,b2 通过 MLP 进行变换得到的。
我们对每个特征维度进行批次归一化,使其均值为0,方差为1。在推断之前,我们还对分类特征添加了截断的高斯噪声;这可以提高对离散特征的性能,因为模型主要在连续数据上进行训练。
表格自注意力 由于我们的表格输入在行和列维度上共享信息,我们在每个 Transformer 层中同时应用行维度和列维度的注意力。给定隐藏空间中的输入
X
h
∈
R
n
,
m
,
d
X_{h} \in \mathbb{R}^{n, m, d}
Xh∈Rn,m,d,表格注意力的输出
Y
h
∈
R
n
,
m
,
d
Y_{h} \in \mathbb{R}^{n, m, d}
Yh∈Rn,m,d 计算如下:
ColAttn
(
X
h
)
=
Softmax
(
Q
col
⊤
K
col
)
V
col
Row
Attn
(
X
h
)
=
Softmax
(
Q
row
⊤
K
row
)
V
row
Y
h
=
ColAttn
(
X
h
)
+
RowAttn
(
X
h
)
+
X
h
\begin{array}{l} \operatorname{ColAttn}\left(X_{h}\right)=\operatorname{Softmax}\left(Q_{\text {col }}^{\top} K_{\text {col }}\right) V_{\text {col }} \\ \operatorname{Row} \operatorname{Attn}\left(X_{h}\right)=\operatorname{Softmax}\left(Q_{\text {row }}^{\top} K_{\text {row }}\right) V_{\text {row }} \\ Y_{h}=\operatorname{ColAttn}\left(X_{h}\right)+\operatorname{RowAttn}\left(X_{h}\right)+X_{h} \end{array}
ColAttn(Xh)=Softmax(Qcol ⊤Kcol )Vcol RowAttn(Xh)=Softmax(Qrow ⊤Krow )Vrow Yh=ColAttn(Xh)+RowAttn(Xh)+Xh
注意力在行和列维度上分别应用,它首先在 n n n 行上收集信息,然后在 m m m 列上收集信息,复杂度为 O ( n 2 + m 2 ) O\left(n^{2}+m^{2}\right) O(n2+m2)。与将表格重塑为长序列相比,这减轻了计算成本,后者需要 O ( n 2 m 2 ) O\left(n^{2} m^{2}\right) O(n2m2) 的复杂度,同时有效地收集和传播整个表格的信息。
带高斯平滑的交叉熵
我们模型的主要任务是选择一个特征和值来分割输入数据。这个过程涉及从输入矩阵 X ∈ R n , m X \in \mathbb{R}^{n, m} X∈Rn,m 中选择一个特定的元素。假设选择了 X i , j X_{i, j} Xi,j,它等价于一个决策,将数据沿着第 j j j 个特征以值 X i , j X_{i, j} Xi,j 进行分割。我们的模型输出和相应的损失函数的设计基于这个分割选择的基本原则。模型的输出经过线性投影,从 R n , m , d \mathbb{R}^{n, m, d} Rn,m,d 缩小到 R n , m , 1 \mathbb{R}^{n, m, 1} Rn,m,1,最终输出在经过 Sigmoid 激活后得到。
我们使用监督学习来训练模型。在真实的决策树中,每个节点包含特征索引和分割值。这等价于对输入表格进行 one-hot 掩码,其中最佳特征和值的选择标记为1,其余标记为0。然而,直接使用这个掩码作为训练信号会引发问题:一些数据点可能具有与最佳分割相同或非常相似的值,屏蔽这些数据点会混淆模型。因此,我们对选择的特征进行了高斯平滑,将真实的分割特征和值表示为
j
∗
j^{*}
j∗ 和
v
∗
v^{*}
v∗,训练目标
M
M
M 如下:
M
=
{
exp
−
(
X
[
:
,
j
]
−
v
∗
)
2
2
σ
2
,
if
j
=
j
∗
0
,
if
j
≠
j
∗
M=\left\{\begin{array}{ll} \exp -\frac{\left(X[:, j]-v^{*}\right)^{2}}{2 \sigma^{2}}, & \text { if } j=j^{*} \\ 0, & \text { if } j \neq j^{*} \end{array}\right.
M={exp−2σ2(X[:,j]−v∗)2,0, if j=j∗ if j=j∗
其中
σ
\sigma
σ 是一个超参数,控制平滑半径。我们使用二元交叉熵(BCE)来计算模型输出和训练目标
M
M
M 之间的损失。
学习计划 我们的训练方法旨在适应来自两种不同算法的混合学习信号,每种算法都有其独特的目标和行为。这个任务很困难。模仿最优决策树算法已经具有挑战性(即近似 NP 难问题的解决),但 MetaTree 还必须学会生成具有更好泛化潜力的分割。
为了有效地训练我们的模型,我们在实验中使用了学习计划(如图3所示)。在第一阶段,重点完全放在从最优 GOSDT 树中学习上。在这个阶段,目标是尽可能地模拟 GOSDT 算法的行为。然后在第二阶段,训练过程将同时使用 GOSDT 和 CART 树的数据(详见第4.1节),以训练 MetaTree。这种两阶段的方法使我们的模型能够吸收两种算法的特点,从而提高泛化能力。(有关训练计划的消融研究,请参见附录A.3。)
实验设置
数据集
我们使用了来自 OpenML(Van- schoren 等,2013年)和 Penn Machine Learning Benchmarks(Romano 等,2021年)以及一个合成的 XOR 数据集的 632 个分类数据集。我们要求每个数据集至少有 1000 个数据点,最多 256 个特征,最多 10 个类别,并且少于 100 个分类特征,没有缺失数据。我们随机选择了 91 个数据集作为留出测试集,用于评估我们模型的泛化能力,同时确保它们及其变体不出现在训练集中。
我们以以下方式生成决策树训练数据集:对于每个数据集,我们首先将其分为训练集和测试集,比例为 70:30;然后我们从训练集中随机选择 256 个数据点,其中每个数据点选择 10 个随机选定的特征维度,并拟合一个 GOSDT 树(Lin 等,2020年)和一个 CART 树(Breiman 等,1984年);然后我们记录两棵树在测试集上的准确率;最后,我们再次随机选择 256 个数据点,为每个数据集生成 10k 棵树。总共,我们为训练生成了 10,820,000 棵树。
我们还在来自 Morris et al. (2023) 的 13 个 Tree-of-prompt 数据集上测试了 MetaTree。这些数据集是从文本分类任务构建的表格数据集;输入 X 是 LLM 对文本附带的一组提示的回答(是或否),输出 Y 是类别标签。成功地在这些数据集上构建树表明 MetaTree 在引导大型语言模型方面具有潜力。此外,由于 MetaTree 是可微分的,它可以直接集成到一些 LLM 的训练过程中。
我们使用以下算法生成了一个合成的 XOR 数据集:首先,在二维边界框 {x|x ∈ [−1*,* 1]²*}* 中随机采样了 256 个数据点;然后根据预先指定的级别(例如,级别 1 的 XOR 有 3 个分割,级别 2 的 XOR 有 15 个分割,根节点的分割可以在 [−1*,* 1] 中随机发生,而其余的分割在分割的边界框内随机采样,参见图 4 中的示例)随机生成了地面真值 XOR 分割,并根据分割分配类别标签;最后,我们添加了标签翻转噪声和额外的噪声特征维度,这些特征维度由 [−1*,* 1] 内的均匀噪声组成。
基线算法
我们使用 GOSDT (Lin et al., 2020) 和 CART (Breiman et al., 1984) 作为我们的基线算法,作为代表性的最优和贪婪决策树算法。对于 GOSDT,我们使用官方实现,在初始标签预热中使用梯度提升决策树,估计器数量为 128,正则化因子为 1e-3。对于 CART,我们使用 sklearn 中的实现 (Pedregosa et al., 2011),将分割准则设置为基尼不纯度。
模型配置
我们使用 LLaMA-2 (Touvron et al., 2023) 作为基础 Transformer。对于 MetaTree,我们将层数设置为 12,头数设置为 12,嵌入维度设置为 768,MLP 维度设置为 3072。
我们从头开始在 GOSDT 数据集上预训练我们的模型,训练收敛后,我们在 GOSDT+CART 数据集上进行微调。与直接在 GOSDT+CART 数据集上训练相比,这种课程设计可以提高性能(如附录 A.3 中所示)。详细的训练超参数请参见附录 A.1。
主要结果
在本节中,我们展示了 MetaTree 在模型之前从未见过的真实世界数据集上的性能(图 1)。我们将其与两个已建立的算法 GOSDT 和 CART 进行比较,并发现它的表现优秀,尤其是在合并多个树时。我们关注三个问题:(1) MetaTree 能否有效地推广到之前未遇到过的真实世界数据?(2) MetaTree 能否生成比其训练时更深的决策树?(3) MetaTree 能否在 LLM 设置中准确地引导模型输出?
推广到新数据集:图 1A 为了回答第一个问题,我们严格评估了 MetaTree 在其训练中排除的 91 个数据集上的性能。对于每个数据集,我们采用标准的 70/30 划分来创建训练集和测试集,然后从训练集中重复采样并运行决策树算法(MetaTree、GOSDT 或 CART)以形成具有指定树数量的树集合,树集合中的大多数预测被视为集合预测,并对所有数据集的准确率进行平均。整个评估过程在 10 次独立运行中复制,并在图中显示标准差作为误差线。
结果显示,MetaTree 在性能上始终明显优于 GOSDT 和 CART。值得注意的是,随着树的数量增加,所有方法的性能都有所提高,并在树的数量达到 60 时趋于稳定。当树的数量较少时,GOSDT 的性能优于 CART;这与 GOSDT 在设计上旨在最优地解决训练集的倾向相吻合。这也导致 GOSDT 的泛化性能具有较高的方差。
推广到更深的决策树:图 1B 除了 MetaTree 能够推广到新数据的能力,我们现在研究 MetaTree 是否能够生成更深的决策树。为了回答这个问题,我们要求 MetaTree 生成深度为 3 的决策树,并与 CART 进行泛化性能比较,类似于前面的评估过程。¹
结果如图 1B 所示。可以观察到,MetaTree 仍然一贯优于 CART,只有在树的数量为 1 时例外,这表明 MetaTree 能够生成超出其训练深度的决策树。我们相信,训练 MetaTree 在更深的决策树上可能会进一步增强这种能力。
MetaTree 能够推广到更深的决策树的一个原因是,它被设计为在每个节点生成分割决策,因此生成的树不依赖于树的深度。此外,该模型已经在深度为 2 的树上进行了训练,即根节点分割和两个子节点分割,我们相信我们的模型可能已经学会了作为归纳算法的行为,从而生成高质量的更深的决策树。
Tree-of-prompt 数据集:图 1C 我们在 13 个 Tree-of-prompt 数据集上评估了 MetaTree,这些数据集由纯分类特征组成,输入是 LLM 对一组提示的回答(是或否),输出是文本的分类标签。图 1C 再次将 MetaTree 与 GOSDT 和 CART 进行了比较。与 GOSDT 和 CART 相比,MetaTree 在所有树的数量上都保持着更高的泛化准确率。随着树的数量的增加,这种趋势尤为明显,显示了 MetaTree 在单个好/坏样本的随机效应被稀释时的鲁棒性。GOSDT 和 CART 的泛化准确率较低,其中 GOSDT 在较小的树数量上表现略好于 CART。
这个评估展示了 MetaTree 在 Tree-of-prompt 数据集上的出色性能,突出了它处理分类特征的能力,并为 LLM 生成的输入和用户查询的输出生成可微分的决策树。

图 4:贪婪算法(如 CART)无法解决需要规划的问题,例如 Level 1&2 XOR。我们展示了 MetaTree 可以学会解决 Level 1 XOR,甚至在一定程度上推广到解决 Level 2 XOR。
表 1:MetaTree(在带有 15% 噪声的 XOR Level 1 上训练)在 XOR 数据集上的相对误差,其中 level={1, 2*}* 和标签翻转噪声率={0%, 5%, 10%, 15%, 20%, 25%}。

分析
在对 MetaTree 的性能进行基准测试之后,我们对其行为和分割策略进行了深入分析。我们的 MetaTree 分析从一个受控环境开始(第 6.1 节),评估 MetaTree 在存在噪声和特征交互的情况下的性能。然后,我们更详细地研究了 MetaTree 在选择贪婪分割和优化分割之间的倾向(第 6.2 节),MetaTree 的内部决策过程(第 6.3 节)以及 MetaTree 的经验偏差-方差分析(第 6.4 节)。
受控环境:带噪声的 XOR
我们在一个受控的环境中评估 MetaTree 模型,在 XOR 数据集上进行评估,其中 level={1,2},标签翻转噪声={0%, 5%, 10%, 15%, 20%, 25%},每个 XOR 级别/噪声比配置的数据集大小为 10k。为了评估性能,我们使用 相对误差 指标,定义为实际准确率与最大可能准确率(= 100% − 标签噪声率)之间的差距。请注意,我们只在 10k 个由 XOR Level 1 生成且带有 15% 标签噪声的树上训练了我们的模型。选择这个特定的训练场景是为了评估模型对噪声的鲁棒性和对更困难问题的适应能力。
如表 1 所示,MetaTree 在抵抗噪声和泛化方面表现出了显著的能力。一旦 MetaTree 学会解决 XOR Level 1 问题,它就能够承受更强的数据噪声(而 MetaTree 只见过 15% 的噪声),并且能够推广到更困难的 XOR Level 2 问题(而 MetaTree 只在 XOR Level 1 上进行了训练)。
我们进一步进行了定性分析,要求 CART 和 MetaTree 为 XOR Level 1&2 问题生成决策树。如图 4 所示的结果对比了两个模型在不同复杂性级别下的决策过程。
MetaTree 选择了哪些分割?
我们的模型是根据 GOSDT 和 CART 的泛化性能选择的混合学习信号进行训练的。我们的目标是弄清楚 MetaTree 是否可以在 GOSDT 和 CART 之间策略性地调整其分割方法。为了回答这个问题,我们随机从剩下的 91 个数据集中每个数据集中随机选择 100 个样本(每个样本包含 256 个数据点),并要求 MetaTree、GOSDT 和 CART 为每个样本生成分割。这种方法确保了三个算法在进行分割决策时提供了相同的数据,从而可以进行有意义的比较。
我们在图5a中绘制了Meta-Tree和CART/GOSDT之间的输出相关性分布,当CART是两者中更好的泛化算法时。同样地,我们在图5b中绘制了Meta-Tree和CART/GOSDT之间的输出相关性,当GOSDT是更好的泛化算法时。我们将输出相关性值分为三个类别(低、中、高相关性),可以观察到Meta-Tree倾向于选择表现更好的算法。
此外,我们在图5c中可视化了相关性差异(CART相关性减去GOSDT相关性)与泛化性能差异(CART的测试准确率减去GOSDT的测试准确率)之间的关系,注意到我们排除了性能差异较小的样本(泛化准确率差异≤0.08)。观察到中等相关性(Pearson相关系数=0.53,p值=0.0011),表明Meta-Tree的分裂策略倾向于与泛化性能一致。
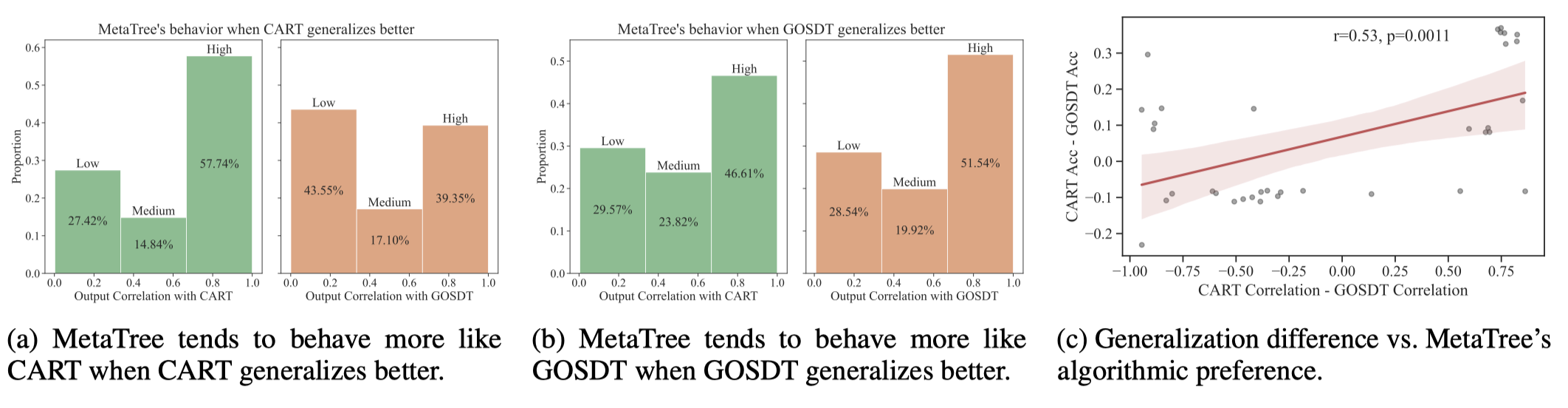
图5:我们展示了Meta-Tree学习适应更好泛化的分裂策略。图(a)和(b)展示了Meta-Tree倾向于选择更有效的泛化策略:在(a)中选择贪婪算法CART,在(b)中选择最优算法GOSDT。在©中,我们展示了Meta-Tree的算法偏好与算法的泛化性能呈正相关。
探索Meta-Tree的决策过程
我们的研究部分受到了对GPT-2进行的logit-lens行为分析的启发(Hanna等人,2023)。他们的研究结果表明,GPT-2在中间层通常对下一个标记形成一个初始猜测,随后的层次对这个猜测进行细化以生成最终的生成分布。基于这个概念,我们旨在调查我们的模型是否存在类似的猜测-细化模式,并探索在Zhou等人(2020)中概述的早期退出策略的可行性。
为此,我们分析了我们模型在每个Transformer层的决策过程。我们可以通过将每个层的中间表示输入到输出模块中来详细研究模型的决策如何演变。图6a展示了一个定性的例子,我们要求Meta-Tree在一个XOR Level 1问题上生成根节点的分裂。我们可以观察到模型在第一层之后就得到了一个合理的分裂。在第9层,模型达到了接近最终输出的分裂,第10层的输出是一个接近真实分裂的备选修订(真实分裂可以是垂直或水平分裂)。
我们进行了定量分析,以研究模型的最终分裂与其中间层中出现的分裂之间的相关性。我们按照Sec. 6.2中详细说明的相同过程,从91个留出的数据集中选择样本,并要求Meta-Tree在这些样本上生成分裂。分裂之间的相关性由应用分裂后的标签分配之间的相关系数确定。该指标本质上衡量了分裂在解剖输入区域方面的一致性。
我们的定量分析结果如图6b所示。值得注意的是,相关性从第1层到第8层逐渐增加,几乎在第9层达到1。然而,在第10层和第11层,相关性显著下降到约0.2。这种模式表明,模型在最初的1到9层中不断改进其进行准确预测的能力,而第10层和第11层可能在决策过程中引入一些分歧或修订。
这一发现为我们了解Meta-Tree的内部决策过程提供了有价值的见解。它提出了在中间层(特别是第9层附近)考虑早期退出策略以提高整体效率的可能性。
偏差-方差分析
最后,我们进行了全面的偏差-方差分析,评估了Meta-Tree、GOSDT和CART在91个留出的数据集上的性能。该分析显示了每个算法在偏差(由于算法学习能力不足或错误的模型假设导致的错误)和方差(对训练集中的小波动敏感性导致的错误)之间的权衡。我们使用经验偏差和方差作为评估指标;对于每个数据集,我们进行了100次重复(N=100),因此每个算法每个数据集有100个决策树模型。算法的经验偏差通过其生成模型的平均输出与真实标签之间的ℓ₂差异计算,而经验方差通过其生成模型的平均输出与每个模型的输出之间的平均ℓ₂差异计算。
结果如图7所示。图中的每个点对应于一个算法在单个数据集上的偏差-方差坐标,x轴表示经验偏差,表示算法与真实函数的平均误差,而y轴表示经验方差,反映算法对不同训练集的敏感性。可以观察到,Meta-Tree表现出较低的经验方差,表明其在不同数据分布情况下的稳健性。

图6:探索Meta-Tree的内部决策过程。

图7:Meta-Tree、GOSDT和CART在91个留出的数据集上的经验偏差-方差比较,每个数据集进行了100次重复。与GOSDT和CART相比,Meta-Tree具有显著较低的方差和稍小的偏差。
讨论
局限性和未来方向 Meta-Tree受到Transformer固有的架构限制的约束。具体而言,Meta-Tree可以处理的数据点和特征的最大数量受到Transformer模型的最大序列长度的限制(详见表2的详细规格)。然而,通过训练一个更大的模型可以缓解这些限制。Transformer处理长序列的能力不断提高,最先进的语言模型(LLMs)(OpenAI,2023)现在能够处理多达128k个标记的序列。虽然Meta-Tree仍然局限于小型数据集,但这项工作展示了学习自适应生成机器学习模型的重要第一步,并将训练大规模LLM留给未来的工作。
结论 我们引入了Meta-Tree,一种基于Transformer的新型决策树算法。它与传统的基于启发式或基于优化的决策树算法不同,利用了Transformer的学习能力来生成强大的决策树模型。Meta-Tree使用来自经典决策树算法的数据进行训练,并展现了根据数据集上下文自适应策略的独特能力,从而实现了更好的泛化性能。该模型在未见过的真实世界数据集上展示了其有效性,并可以推广生成更深的决策树。我们对Meta-Tree的行为、内部决策过程和偏差-方差特性进行了全面分析。这项工作展示了深度学习模型在算法生成方面的潜力,将其范围从预测标签扩展到自动模型创建的领域。它学习和改进已有算法的能力为机器学习领域的研究和应用开辟了新的方向。
更广泛的影响
本文的目标是推进机器学习领域的发展。我们的工作可能会产生许多潜在的社会影响,但我们认为没有必要在此特别强调。

























 527
527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










