狐猴优化算法（LO），原理公式详解，附matlab代码

最新推荐文章于 2025-04-04 09:14:11 发布

淘个代码_

最新推荐文章于 2025-04-04 09:14:11 发布

阅读量1.4k

点赞数 19

本文链接：https://blog.csdn.net/woaipythonmeme/article/details/135891105

版权

文章介绍了AmmarKamalAbasi等人在2022年提出的狐猴优化算法（LemursOptimizer），它模仿狐猴的跳跃和舞蹈行为进行搜索。算法包含探索和开发两个阶段，通过元启发式策略寻找最优解。在MATLAB代码中详细展示了算法流程和参数设置。算法在CEC2005函数集测试中展示了性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

狐猴优化算法(Lemurs Optimizer，LO)由Ammar Kamal Abasi等人于2022年提出，是一种新型群智能优化算法，该算法模拟狐猴的跳跃和跳舞行为，具有结构简单，思路新颖，搜索速度快等优势。该成果于2022年发表在知名SCI期刊Applied Sciences上，目前在谷歌学术上被引14次。

在该算法中，我们使用狐猴的两种主要行为作为灵感：跳跃和舞蹈。

狐猴跳起来，跳到空中，直立地坐在附近的树枝上，双手和脚紧紧地抓住树干。它们可以在几秒钟内从树干跳到10米高。当树与树之间的空间变得太大时，狐猴会下到地面，交叉长度超过100米，它们会直立并水平跳跃，双臂伸展到一侧，从胸部到头部高度上下摆动，表面上是为了保持平衡。

使用元启发式的两个优化阶段，探索和开发，与这两种运动行为非常相似。探索阶段的主要目标是让狐猴跳跃到不同的区域，以在搜索空间中找到狐猴的最佳位置。然而，在舞蹈中心的狐猴会朝一个方向移动到附近最好的狐猴位置，这在开发阶段很有用

1、算法原理

（1）搜索阶段

在探索阶段，我们利用了dance-hup行为，跳跃行为有助于狐猴算法挖掘搜索空间。我们认为每个解都是一只狐猴，每个向量代表狐猴的一个单独的坐标，同时还为每个解决方案分配最佳位置，该位置与解决方案的适应度函数值相关。结果，狐猴会改变它们的位置矢量，朝最整洁的狐猴跳起，或者跳到全范围内最优的狐猴身上。

狐猴的集合用矩阵表示，因为LO算法是基于种群的算法，其数学表达式如下：其中T表示狐猴在规模为s×d的种群矩阵中的集合，d表示决策变量，s表示候选解。通常，解i中的决策变量j由如下公式随机生成：其中函数rand()产生一个范围为(1,2，…，MAX_INT)，其中MAX_INT为所能生成的最大整数，变量j的离散上下限用[lbj, ubj]表示。

（2）开发阶段

具有较低适应值的狐猴倾向于从具有较高适应值的狐猴改变其决策变量。这意味着总的狐猴的整体适应值随着迭代而提高。在每次迭代中，基于它们的适应度值来组织狐猴，其中一个被选为全局最佳狐猴（即，gb1）和对于每只狐猴选择一只作为最佳最近的狐猴（即，bnl）。

在这个方向上，每次迭代都会使用以下两个选项给解i中的决策变量j赋值，分别为

(1)该值从全局最优的狐猴中选择

(2)该值从最接近的狐猴中选择，其数学表达式如下：其中，l(i, j)表示当前狐猴的j值，l(bnl, j)表示当前狐猴l(i, j)的最接近狐猴的j值，l(gbl, j)表示全局最优狐猴，自由风险率(FRR)表示部队中所有狐猴的风险率，rand表示[0,1]之间的随机数。

根据以上公式，可以看出FRR的概率是LO算法的主要系数。该系数的公式如下：其中Low_Risk_Rate和High_Risk_Rate表示固定的预定义值，MaxIter为最大迭代次数，CurrIter表示当前迭代，注意，Low_Risk_Rate和High_Risk_Rate的目的是确定FRR的最小值和最大值。下图为该算法的高风险率和低风险率概念模型。

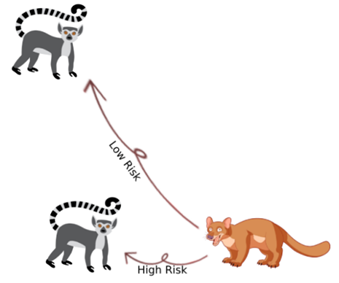
2、算法优化步骤

1:设置LO参数(迭代次数、维数(Dim)、解决方案数、下限(LB)、上限(UB)、低风险率、高风险率)。
2:生成狐猴种群。
3:在当前迭代不等于迭代次数开始
4:评估所有狐猴的目标函数。
5:使用公式(4)计算free risk rate (FRR)
6: Update the Global Best Lemur (gbl)
7: for each lemur indexed by i do
8: Update the Best Nearest Lemur (bnl).
9: for each decision variable in Lemur i indexed by j do
10:设置random([0,1])为rand。
11: if rand < JumpingRrate then 
12:使用案例一更新决策变量j。
13: else
14:使用案例二更新决策变量j。
15: end if
16: end for
17: end for
18: end while
19:返回全局最佳狐猴。

结果展示

在CEC2005函数集测试，结果如下：

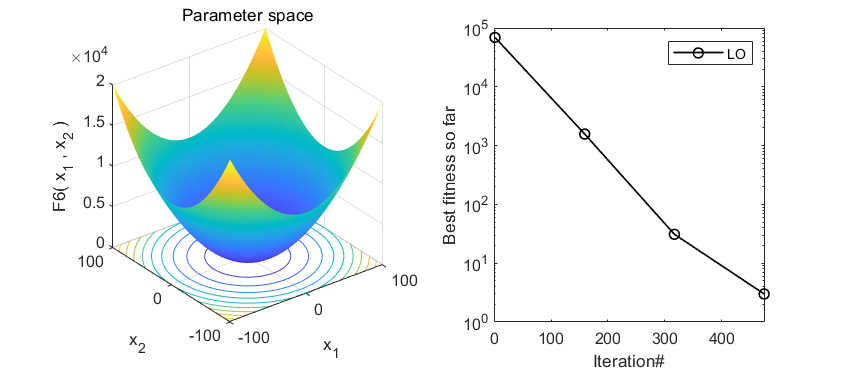
MATLAB核心代码

function [best_score,bestx,conv] = LO (PopSize,Max_iter,lb,ub,dim,fobj)




jumping_rate_min=0.1;   % JR0.1  0.1, 0.2, 0.3, 0.4, 0.5
jumping_rate_max=0.5;   %     0.9, 0.8, 0.7, 0.6, 0.5
% Initializing arrays
swarm = zeros(PopSize, dim);


% Initialize the population/solutions
swarm = initialization(PopSize, dim, ub, lb);


for i = 1:PopSize
    ObjVal(i) = fobj(swarm(i, :));
end


%===================== loop ===================================


itr = 0; % Loop counter


while itr < Max_iter


    jumping_rate = jumping_rate_max - itr * ((jumping_rate_max - jumping_rate_min) / Max_iter);
    % swarm looking to go away from killer "free risk started too high "
    [sorted_objctive, sorted_indexes] = sort(ObjVal);


    for i = 1:PopSize


        current_solution = find(sorted_indexes == i);  % possition of the current solution
        near_solution_postion = current_solution - 1;  %
        if near_solution_postion == 0
            near_solution_postion = 1;
        end
        near_solution = sorted_indexes(near_solution_postion);


        [cost, best_solution_Index] = min(ObjVal);


        NewSol = swarm(i, :);


        for j = 1: dim


            r = rand(); % select a number within range 0 to 1.


            if (r < jumping_rate)


                NewSol(j) = swarm(i, j) + abs(swarm(i, j) - swarm(near_solution, j)) * (rand - 0.5) * 2;


                % manipulate range between lb and ub
                if (size(lb,2)~=1)
                    NewSol(j) = min(max(NewSol(j), lb(j)), ub(j));
                else


                    NewSol(j) = min(max(NewSol(j), lb), ub);
                end
            else
                % for long jumbing will take from best solution
                NewSol(j) = swarm(i, j) + abs(swarm(i, j) - swarm(best_solution_Index, j)) * (rand - 0.5) * 2;
                % manipulate range between lb and ub


                if (size(lb,2)~=1)
                    NewSol(j) = min(max(NewSol(j), lb(j)), ub(j));
                else


                    NewSol(j) = min(max(NewSol(j), lb), ub);
                end


            end


        end


        %evaluate new solution
        ObjValSol = fobj(NewSol);




        % Update the curent solution  & Age of the current solution
        if (ObjVal(i) > ObjValSol)
            swarm(i, :) = NewSol;
            ObjVal(i) = ObjValSol;
        end
    end




    itr = itr + 1;
    [best_score,idx] = min(ObjVal);
    conv(itr)=best_score;
    bestx = swarm(idx, :);
    
end
end

参考文献

[1] Abasi A K, Makhadmeh S N, Al-Betar M A, et al. Lemurs optimizer: A new metaheuristic algorithm for global optimization[J]. Applied Sciences, 2022, 12(19): 10057.

完整代码获取方式：后台回复关键字：

TGDM100