智能算法之天鹰优化算法(AO)，原理公式详解，附matlab代码

天鹰优化器(AO)是由Laith Abualigah等人提出了一种新的基于种群的元启发式优化方法，AO算法受到自然界中天鹰在捕获猎物过程中行为的启发，模拟了天鹰在狩猎过程中的行为，其中包含了天鹰狩猎时每个步骤的动作。该算法发表于2021年SCI期刊2区Computers & Industrial Engineering，目前被引次数1280余次。足以见其优势！

天鹰的狩猎方式分为以下四种：

(1)垂直弯曲的高空飞翔，用来狩猎飞行中的鸟类。

(2)轮廓飞行和短滑翔攻击，被公认为是最常用的方法，天鹰在地面上的低水平上升，不管猎物是在跑还是在飞，都紧追不舍。

(3)低飞慢降攻击，在这个过程中，天鹰低伏在地，然后逐渐向猎物发起猛攻。

(4)行走并抓住猎物，它被用来将大型猎物(如鹿或羊)的幼仔拉出它们的区域。

算法原理

1.扩展探索阶段

图1.天鹰的垂直弯曲高空翱翔

天鹰通过高飞和垂直弯曲来识别猎物区域，选择最佳狩猎区域。 

其中，  是  的下一个迭代的解，由第一个搜索方法  生成。  是第次迭代前的最优解，反映了猎物的近似位置。  用于通过迭代次数控制扩展搜索。  表示第t次迭代时连接的当前解的位置均值，由式(4)计算。为0到1之间的随机值。t和T分别表示当前迭代次数和最大迭代次数。 2.缩小探索范围

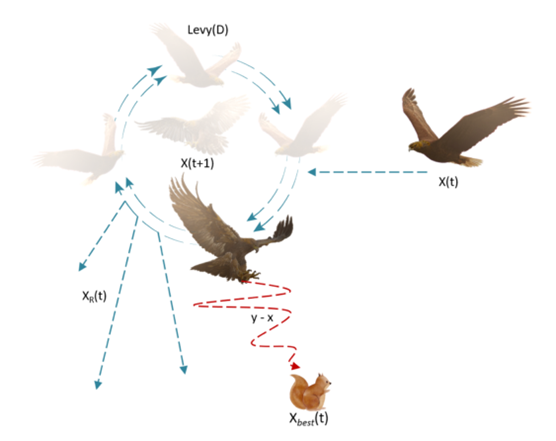
图2.天鹰的轮廓飞行和短滑翔攻击

当从高空发现猎物区域时，天鹰会在目标猎物上方盘旋，准备好着陆，然后发动攻击。这种方法称为轮廓飞行和短滑翔攻击。

其中  是的下一个迭代的解，它是由第二个搜索方法(  )生成的。D为维数空间，Levy(D)为飞行分布函数。  为第t次迭代时在范围内取的随机解。  其中s是一个固定到0.01的常数值，  和μ是0到1之间的随机数。 其中  为固定为1.5的常数值。用y和x表示搜索中的螺旋形状，计算如下: 

 其中： 

  取1到20之间的值，用来固定搜索周期数，U固定为0.00565。  是从1到搜索空间长度(Dim)的整数，  是一个固定为0.005的小值。

3: 低飞慢降攻击

图3.天鹰的低飞慢降攻击行为

当精确指定了猎物的区域，且天鹰准备着陆和攻击时，天鹰会垂直下降并进行初步攻击，以发现猎物的反应。这种方法叫做低飞慢降攻击。在这里，天鹰利用目标选定的区域接近猎物并攻击。  其中  是的下一个迭代的解，它是由第三种搜索方法  生成的。  为第t次迭代前猎物的近似位置(即得到的最佳解)，  为第次迭代时当前解的均值。  和  是采用的调整参数，固定到一个小值[都取0.1时效果最好]。

4: 缩小利用范围

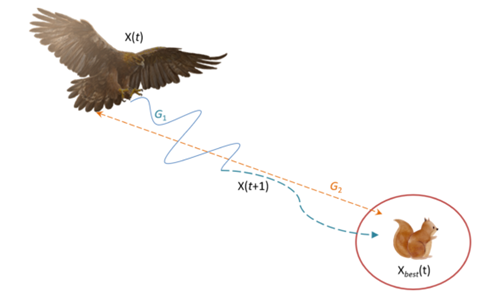
在第四种方法中，当天鹰接近猎物时，它会根据猎物的随机运动在陆地上攻击猎物。这种方法叫做行走并抓住猎物。  其中  是的下一个迭代的解，它是由第四种搜索方法生成的。QF表示用于均衡搜索策略的质量函数。  表示在猎物逃跑过程中用来跟踪猎物的天鹰的各种运动。  的值从2下降到0，这表示在猎物潜逃过程中用来跟踪猎物的天鹰从第一个位置到最后一个位置(t)的飞行斜率。  是第次迭代时的当前解。 

 结果展示

以为CEC2005函数集为例，进行结果展示：

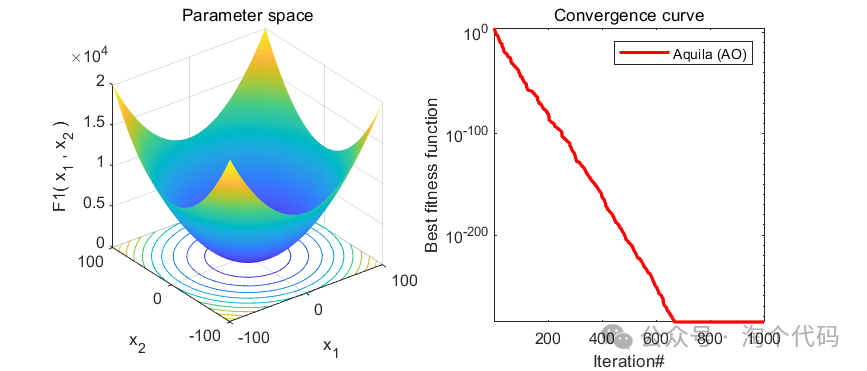
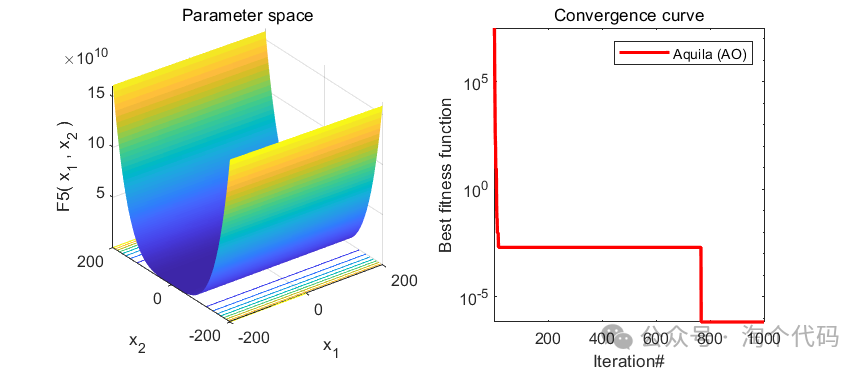
 MATLAB核心代码

function [Best_FF,Best_P,conv]=AO(N,T,LB,UB,Dim,F_obj)
Best_P=zeros(1,Dim);
Best_FF=inf;


X=initialization(N,Dim,UB,LB);
Xnew=X;
Ffun=zeros(1,size(X,1));
Ffun_new=zeros(1,size(Xnew,1));


t=1;
alpha=0.1;
delta=0.1;


while t<T+1
    for i=1:size(X,1)
        F_UB=X(i,:)>UB;
        F_LB=X(i,:)<LB;
        X(i,:)=(X(i,:).*(~(F_UB+F_LB)))+UB.*F_UB+LB.*F_LB;
        Ffun(1,i)=F_obj(X(i,:));
        if Ffun(1,i)<Best_FF
            Best_FF=Ffun(1,i);
            Best_P=X(i,:);
        end
    end
    
    
    G2=2*rand()-1; % Eq. (16)
    G1=2*(1-(t/T));  % Eq. (17)
    to = 1:Dim;
    u = .0265;
    r0 = 10;
    r = r0 +u*to;
    omega = .005;
    phi0 = 3*pi/2;
    phi = -omega*to+phi0;
    x = r .* sin(phi);  % Eq. (9)
    y = r .* cos(phi); % Eq. (10)
    QF=t^((2*rand()-1)/(1-T)^2); % Eq. (15)
        %-------------------------------------------------------------------------------------
    for i=1:size(X,1)
        %-------------------------------------------------------------------------------------
        if t<=(2/3)*T
            if rand <0.5
                Xnew(i,:)=Best_P(1,:)*(1-t/T)+(mean(X(i,:))-Best_P(1,:))*rand(); % Eq. (3) and Eq. (4)
                Ffun_new(1,i)=F_obj(Xnew(i,:));
                if Ffun_new(1,i)<Ffun(1,i)
                    X(i,:)=Xnew(i,:);
                    Ffun(1,i)=Ffun_new(1,i);
                end
            else
                %-------------------------------------------------------------------------------------
                Xnew(i,:)=Best_P(1,:).*Levy(Dim)+X((floor(N*rand()+1)),:)+(y-x)*rand;       % Eq. (5)
                Ffun_new(1,i)=F_obj(Xnew(i,:));
                if Ffun_new(1,i)<Ffun(1,i)
                    X(i,:)=Xnew(i,:);
                    Ffun(1,i)=Ffun_new(1,i);
                end
            end
            %-------------------------------------------------------------------------------------
        else
            if rand<0.5
                Xnew(i,:)=(Best_P(1,:)-mean(X))*alpha-rand+((UB-LB)*rand+LB)*delta;   % Eq. (13)
                Ffun_new(1,i)=F_obj(Xnew(i,:));
                if Ffun_new(1,i)<Ffun(1,i)
                    X(i,:)=Xnew(i,:);
                    Ffun(1,i)=Ffun_new(1,i);
                end
            else
                %-------------------------------------------------------------------------------------
                Xnew(i,:)=QF*Best_P(1,:)-(G2*X(i,:)*rand)-G1.*Levy(Dim)+rand*G2; % Eq. (14)
                Ffun_new(1,i)=F_obj(Xnew(i,:));
                if Ffun_new(1,i)<Ffun(1,i)
                    X(i,:)=Xnew(i,:);
                    Ffun(1,i)=Ffun_new(1,i);
                end
            end
        end
    end
    %-------------------------------------------------------------------------------------
    if mod(t,100)==0
        display(['At iteration ', num2str(t), ' the best solution fitness is ', num2str(Best_FF)]);
    end
    conv(t)=Best_FF;
    t=t+1;
end


end
function o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;
end

参考文献

[1] Abualigah L , Yousri D , Elaziz M A , et al. Matlab Code of Aquila Optimizer: A novel meta-heuristic optimization algorithm[J]. Computers & Industrial Engineering, 2021.

完整代码获取方式：后台回复关键字：

TGDM900

点击下方卡片关注，获取更多代码