智能算法之人工兔优化算法(ARO)，原理公式详解，附matlab代码

人工兔优化算法（Artificial rabbits optimization，ARO）是一种受自然启发的群智能优化算法。ARO算法的灵感来源于自然界中兔子的生存策略，包括迂回觅食和随机躲藏。迂回觅食策略迫使兔子吃其他兔子巢穴附近的草，这可以防止它的巢穴被捕食者发现。随机躲藏策略可以让兔子在自己的洞穴中随机选择一个洞穴躲藏，这样可以减少被敌人捕获的可能性。此外，兔子的能量收缩会导致其从迂回觅食策略向随机躲藏策略转变。该算法对这种生存策略进行数学建模，以开发一种新的优化器。

该成果于2022年发表在计算机领域一区期刊Engineering Applications of Artificial Intelligence上，目前在谷歌学术上被引率285次。

1、算法原理

（1）绕道觅食(探索)

在觅食时，兔子会寻找远处，而忽略近在咫尺的东西。它们只吃其他地区的草，而不吃自己地区的草，这种觅食行为被称为迂回觅食。在ARO中，假设群中的每只兔子都有自己的区域，有一些草和d个洞，并且兔子总是随机访问彼此的位置进行觅食。事实上，在觅食时，兔子很可能会在食物来源周围捣乱，以获得足够的食物。因此，ARO的绕行觅食行为表明，每个搜索个体倾向于向群体中随机选择的另一个搜索个体更新自己的位置，并增加了一个扰动。提出了兔子迂回觅食的数学模型:

式中vi(t+1)为第i次迭代时，兔子在t+1时刻的候选位置，xi(t)为ith兔子在t时刻的位置，n为兔子种群的大小，d为问题的维数，T为最大迭代次数，round表示舍入到最接近的整数，randperm返回整数1到d的随机排列，r1、r2、r3为(0,1)中的三个随机数，L为运行长度，表示绕行觅食时的移动速度，n1服从标准正态分布。

在公式中中，扰动可以帮助ARO避免局部极值并进行全局搜索。运行长度L可以在初始迭代时产生更长的步长。而这个长度可以在以后的迭代中生成更短的步骤。C是一个映射向量，它可以帮助算法在觅食行为中随机选择随机数量的搜索个体元素进行突变。R为奔跑算子，用来模拟兔子的奔跑特性。

（2）随机隐藏(利用)

为了躲避捕食者，兔子通常会在巢穴周围挖一些不同的洞来躲藏。在ARO算法中，在每次迭代中，兔子总是沿着搜索空间的每个维度在它周围产生d个洞穴，并且它总是从所有洞穴中随机选择一个藏身，以减少被捕食的概率。

由上式可知，沿每个维度在兔子附近产生d个洞。H是隐藏参数，在迭代过程中随随机扰动从1线性减小到1/T。根据这个参数，最初，这些洞是在兔子的一个更大的邻居中产生的。随着迭代次数的增加，这个邻域也会减少。

兔子经常受到捕食者的追逐和攻击。为了生存，兔子需要找一个安全的地方躲藏。因此，他们拒绝随机选择一个洞穴从他们的洞穴庇护，以避免被抓住。为了对这种随机隐藏策略进行数学建模，提出了以下等式：

其中，bi,r表示随机选择的洞穴，用于隐藏其d个洞穴，并且，r4和r5是（0，1）中的两个随机数。

在实现迂回觅食和随机隐藏两者之一之后，第二只兔子的位置更新为：

该等式表示，如果第11只兔子的候选位置的适应度比当前兔子的适应度好，则兔子将放弃当前位置并停留在候选位置。

（3）能源收缩（从勘探转向开采）

在ARO中，兔子总是倾向于在迭代的初始阶段频繁地执行迂回觅食，而在迭代的后期阶段频繁地执行随机隐藏。这种搜索机制源于兔子的能量，它会随着时间的推移而逐渐缩小。因此，设计了一个能量因子来模拟从勘探到开采的转换。ARO中的能量因子定义如下：

其中r是（0，1）中的随机数。下图描绘了能量因子的行为曲线。

为了研究能量因子对算法搜索行为的影响，计算了A>1的概率。

其中， 

下图中描绘了取决于能量因子的搜索机制。

在迭代过程中绕道觅食的概率约为0.5。换句话说，ARO算法在迭代过程中执行迂回觅食和随机隐藏的量几乎相同，这对平衡探索和利用做出了显著贡献。ARO的流程图和伪代码如图所示

2、结果展示

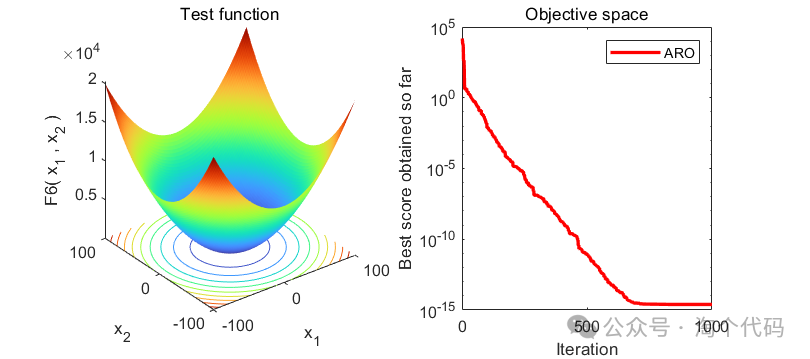
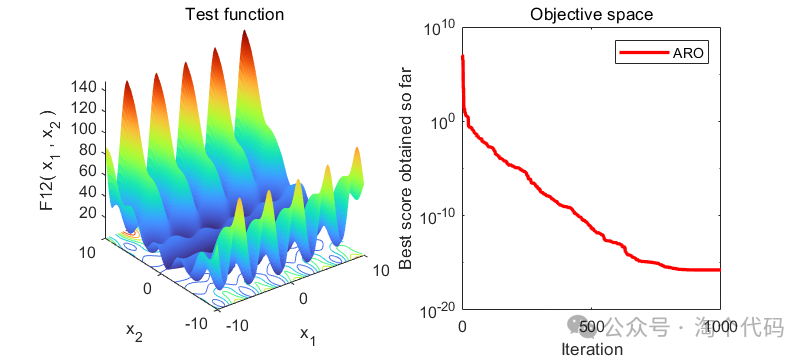
3、MATLAB核心代码

%%% Artificial Rabbits Optimization (ARO) for 23 functions %%%
function [BestX,BestF,HisBestF]=ARO(nPop,MaxIt,Low,Up,Dim,fitness)
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    % FunIndex: Index of function.                       %
    % MaxIt: Maximum number of iterations.               %
    % PopSize: Size of population.                       %
    % PopPos: Position of rabbit population.             %
    % PopFit: Fitness of population.                     %
    % Dim: Dimensionality of prloblem.                   %
    % BestX: Best solution found so far.                 %
    % BestF: Best fitness corresponding to BestX.        %
    % HisBestF: History best fitness over iterations.    %
    % Low: Low bound of search space.                    %
    % Up: Up bound of search space.                      %
    % R: Running operator.                               %
    % L:Running length.                                  %
    % A: Energy factor.                                  %
    % H: Hiding parameter.                               %
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


PopPos=zeros(nPop,Dim);
PopFit=zeros(nPop,1);


for i=1:nPop
    PopPos(i,:)=rand(1,Dim).*(Up-Low)+Low;
    PopFit(i)=fitness(PopPos(i,:));
end


BestF=inf;
BestX=[];


for i=1:nPop
    if PopFit(i)<=BestF
        BestF=PopFit(i);
        BestX=PopPos(i,:);
    end
end


HisBestF=zeros(MaxIt,1);


for It=1:MaxIt
    Direct1=zeros(nPop,Dim);
    Direct2=zeros(nPop,Dim);
    theta=2*(1-It/MaxIt);
    for i=1:nPop
        L=(exp(1)-exp(((It-1)/MaxIt)^2))*(sin(2*pi*rand)); %Eq.(3)
        rd=ceil(rand*(Dim));
        Direct1(i,randperm(Dim,rd))=1;
        c=Direct1(i,:); %Eq.(4)
        R=L.*c; %Eq.(2)
        
        A=2*log(1/rand)*theta;%Eq.(15)


        if A>1


            K=[1:i-1 i+1:nPop];
            RandInd=K(randi([1 nPop-1]));
            newPopPos=PopPos(RandInd,:)+R.*( PopPos(i,:)-PopPos(RandInd,:))...
                +round(0.5*(0.05+rand))*randn; %Eq.(1)
        else


            Direct2(i,ceil(rand*Dim))=1;
            gr=Direct2(i,:); %Eq.(12)
            H=((MaxIt-It+1)/MaxIt)*randn; %Eq.(8)
            b=PopPos(i,:)+H*gr.*PopPos(i,:); %Eq.(13)
            newPopPos=PopPos(i,:)+ R.*(rand*b-PopPos(i,:)); %Eq.(11)


        end
        newPopPos=SpaceBound(newPopPos,Up,Low);
        newPopFit=fitness(newPopPos);
        if newPopFit<PopFit(i)
            PopFit(i)=newPopFit;
            PopPos(i,:)=newPopPos;
        end


    end


    for i=1:nPop
        if PopFit(i)<BestF
            BestF=PopFit(i);
            BestX=PopPos(i,:);
        end
    end


    HisBestF(It)=BestF;


end

参考文献

[1]Wang L, Cao Q, Zhang Z, et al. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems[J]. Engineering Applications of Artificial Intelligence, 2022, 114: 105082.

完整代码获取方式：后台回复关键字：

TGDM166

点击下方卡片关注，获取更多代码