OpenGL相关变换说明

OpenGL相关变换说明

---

在分析OpenGL的相关变换前，让我们首先来看下一下这张图，有一个总的概念。

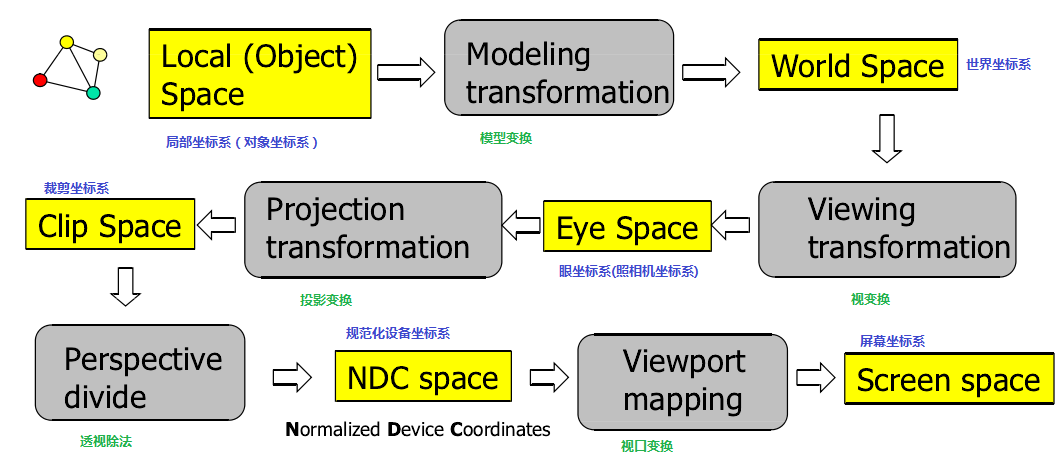
图1. OpenGL相关变换

一、模型变换 (model transformation)

简单来说，我们需要将我们手上的数据模型（可能是一个三角形、也可能是一个篮球的），从原始的本地坐标系（Local Space）变换到OpenGL的世界坐标系（World Space）内的操作就叫做模型变换。就拿简单的篮球模型来说，在我们设计导出的模型，应该中心点是(0,0,0)，篮球的直径可能是0.5，那么我们需要放到世界坐标系的相应位置（0.5，0.5，0.5），大小变为0.1的单位长度，这样的操作就是模型变换，其中我们使用了平移和缩放两个操作。
模型变换包括平移(translation)、缩放(scale)、旋转(rotation)、镜像(reflection)、错切(shear)等操作，想要了解详细的信息以及相关的例子，可以点击这里。

二、视变换(View Trasformation)

视变换就是将物体从世界坐标系(World Space)变换到眼坐标系或称为相机坐标系(Eye Space)。这个概念听起来有点虚，让我们首先来看下面一张图。在第一步中我们将物体移到了OpenGL坐标系中了，但是最终还是需要成像到相应的设备中，那么需要有一个辅助的观察者，这里引入虚构的相机的概念。也就是最终呈现在屏幕中的内容，都首先会呈现在该相机中。既然用相机看世界，我们需要知道有3个变量：1）相机的位置 2）相机对焦于哪个点 3) 相机的正方向。这分别对应于lookAt函数中的(eyeX,eyeY,eyeZ)、(centerX,centerY,centerZ)、(upX,upY,upZ)。如果想具体的了解其中的原理，请点击这里。

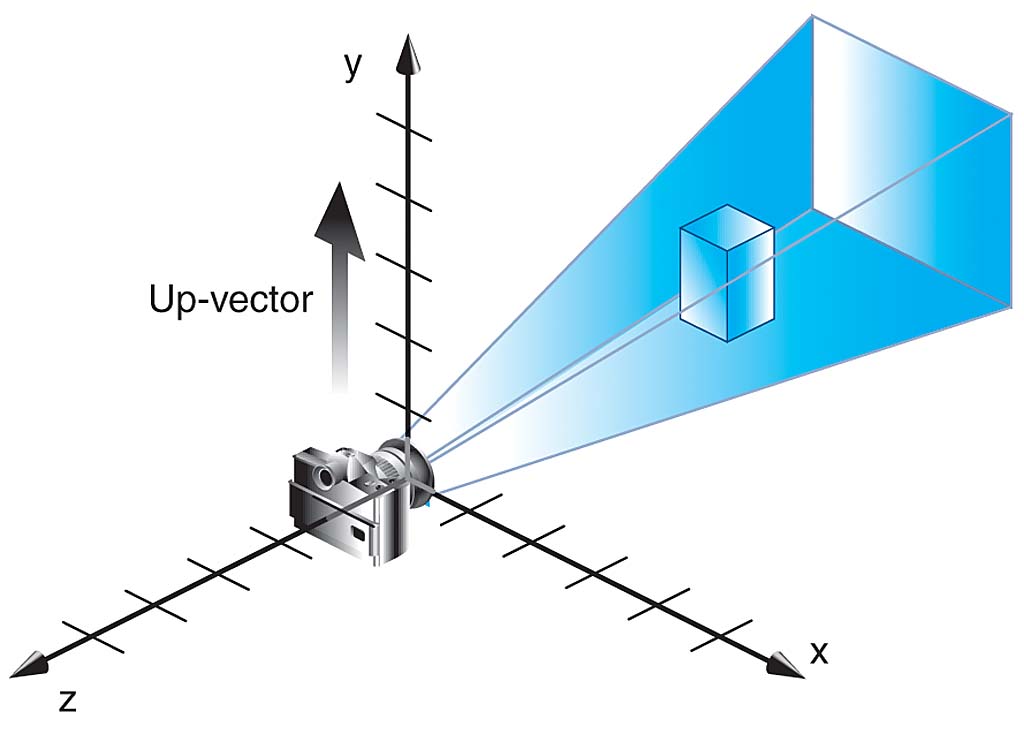
图2. OpenGL中假象的相机模型

三、投影变换(projetiton transformation)

OpenGL最终的渲染设备是2D的，我们需要将3D表示的场景转换为最终的2D形式，前面使用模型变换和视变换将物体坐标转换到照相机坐标系后，需要进行投影变换，将坐标从相机—》裁剪坐标系，经过透视除法后，变换到规范化设备坐标系(NDC)，最后进行视口变换后，3D坐标才变换到屏幕上的2D坐标，这个过程如图1所示。
投影变换通过指定视见体(viewing frustum)来决定场景中哪些物体将可能会呈现在屏幕上。在视见体中的物体会出现在投影平面上，而在视见体之外的物体不会出现在投影平面上。投影包括很多类型，OpenGL中主要考虑透视投影(perspective projection)和正交投影( orthographic projection)。两者之间存在很大的区别，如下图所示：

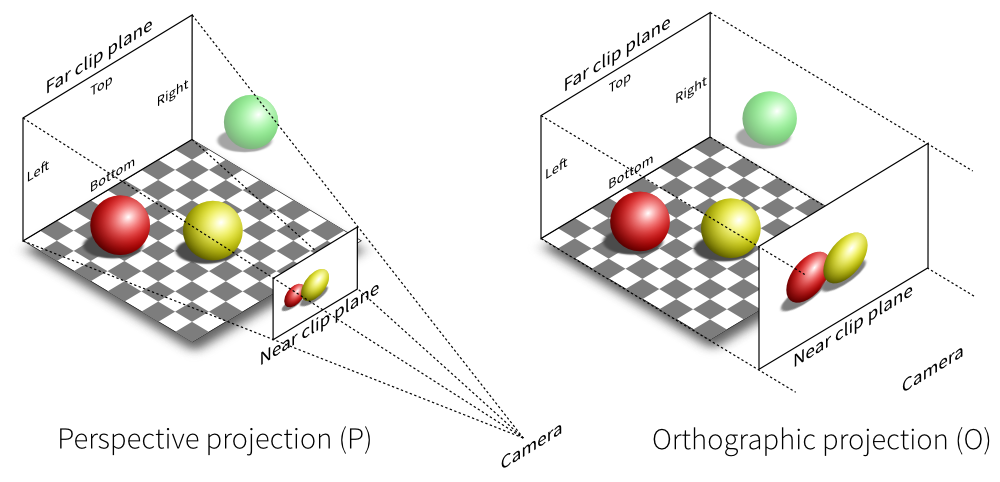
图3. 正交投影和透视投影

上面的图中，红色和黄色球在视见体内，因而呈现在投影平面上，而绿色球在视见体外，没有在投影平面上成像。

指定视见体通过(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble nearVal, GLdouble farVal)6个参数来指定。注意在相机坐标系下，相机指向-z轴，nearVal和farVal表示的剪裁平面分别为:近裁剪平面z=−nearVal，以及远裁剪平面z=−farVal。
OpenGL中，通过frustumM分别设置远裁剪平面的left、right、bottom、top以及near和far的值。具体的投影的推导过程可以点击这里。

为什么需要设定近平面和远平面？
最后投影的结果是一个x,y,z都是(-1,1)的立方体内，近平面可以理解为z=-1，远平面理解为z=1。所以超出这个范围的物体都为不可视。

如果你还是不是很清楚以上的概念，可以点击这里，Jamie King 在YOUTUBE上的教学视频，全英文没有字幕，但是讲的英语都比较通俗，比较好听懂。

四、视口变换(ViewPort Mapping)

视口变换是将NDC坐标转换为显示屏幕坐标的过程，如下图所示：

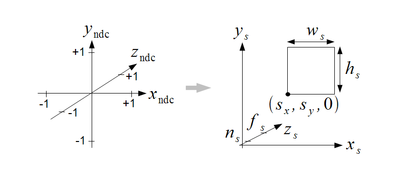
图4. 视口变换示意图

OpenGL中通过glViewport函数进行设置。
因为投影变换的结果是一个x,y,z都是(-1,1)的立方体，而最终我们需要将该立方体所代表的东西显示到终端上。以一个屏幕像素为720x1280的手机作为例子，最终openGL的在屏幕上的二维坐标为x,y都为(-1，1)，但是x轴和y轴的一个距离明显代表有所不同。比如一个通过透视变换的是一个边长为1的正方形，如果不进行视口变换，那么显示出来是一个厂方形，为什么？因为x轴的1长度=360像素，y轴的1长度=640像素。所以必须进行视口变换才能让显示正常。