极值的充分条件应用

极值点的判定，在高中和大学高数中都是一个不太清晰的地方，一般有三条充分条件可以判定一个点是否为极值

这个定理，是高中最常使用的判定极值点的定理，这个定理要判断f’(x)在x0附近的情况，但有时候判断f'(x）在x0左右的情况并不容易，所以在高中往往后求二阶导师，然后通过二阶导数单调性在判断f'(x）在x0附近的情况，这实际上暗含了极值的第二个充分条件

这个定理其实十分好用，因为实际上只要知道f'(x0)=0, 并且f''(x0) >0 ,就可以判定极小值，并不需要任何x0附近的信息。但问题来了，如果二阶导数也为0怎么办？，有没有高效的方法？

极值存在的第三充分定理。

来看一道例子

 、

这道题目第一问其实就暗示了当a=0时，x=0，f(x)其实不是极值点。

        

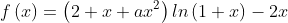
我们知道，一个多项式多项式在0处有极值，且f(0)=0, 其一定是偶数项多项式，即偶函数。（这个很容易证明），即奇数次幂的系数要为0。我们取ln(1+x）的三阶泰勒展开

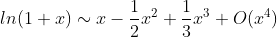
令x^3 系数为0， 立即得到 a = -1/6

这种方法的令一种解释：我们想知道f(x) 在0处的n阶导数值有以下做法

1. 直接暴力求导，令x=0即可

2. 利用泰勒展开式(在x=0处展开）

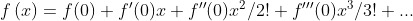
以上展开并不需要直接计算导数得到，可以通过已知展开函数的多项式运算得到。上面的等式中，通过展开ln(1+x)间接计算了f(x)的在0处的n阶导数。在根据极值的第三充分条件，立即得到三阶导数为0，即和前面一样。

明白了这些，在试卷上直接可以这么写：、

显然，f'(0)=0, f''(0)=0, f'''(0)=3!*(2/3-1/2+a）

根据极限的第三充分条件，f'''(0)=0, 所以 a=-1/6。

这种方法实际上绕开了直接对f(x)求导，利用泰勒展开简阶的计算了f'''(0)的值。在考研数学中这种方法很常见，仅针对这道题在高考考场上可能会被扣2分左右，但肯定有大量的分，因为这道题目的答案并不好算。