场曲

像场弯曲时因镜片缺陷，使垂直于主光轴的物平面上发出的光经透镜成像后，清晰的最佳实像面不是平面而是一个曲面的一种像差。1839年匈牙利物理学家约瑟夫佩兹瓦尔最先从物理学角度阐明像场弯曲的原理，为纪念他，像场弯曲也称佩兹瓦尔像场弯曲。

像场弯曲起源于透镜成像的基本规律，对于同一透镜，距离远的物体成像近，反之，距离近的物体，成像远。如图 平面的点离镜头近成像与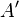点；平面中的点，由于离透镜比点远，因此，点经透镜成像于点，点就得比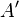点离镜头近^[1]。弯曲的像场称为佩兹瓦尔曲面。

1839年，佩兹瓦尔证明，对于一个光学镜头组，如果镜头没有其他像差，

它的像场弯曲的曲率^[2]

其中

为曲面的曲率半径。 为像场弯曲的曲率半径。

称为佩兹瓦尔和。

佩兹瓦尔证明佩兹瓦尔和和镜头的孔径、光圈位置、镜片厚度、镜片间的空气间隙无关^[3]。

一个有多个互相由空气隔离的薄镜片构成的镜头，其佩兹瓦尔和，其中 是薄镜片的度数，是镜片材料的折射率。