学好机器学习必会的统计学知识（第一篇）

引言

在机器学习应用中，我们不可能离开数据。没有了数据，机器学习算法就像没有了灵魂。更好地理解数据，可以使我们把它更好地应用在机器学习上。在这篇文章中，我会介绍一些在统计学中，理解数据的一些重要概念，从而使大家更准确地操作数据，玩转数据。

频率(frequency)和相对频率(relative frequency)

为了更好地解释这些数学概念，我用Iris数据集实例来说明频率和相对频率。如果大家不熟悉这个数据集没有关系，下面我用具体的R代码来看看这个数据集的细节。

> names(iris)
[1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width"  "Species"     
> str(iris)
'data.frame':   150 obs. of  5 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
> summary(iris)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500                  

通过上面代码我们可以看出，总共有150个observations，总共有3个物种，分别是：virginica、setosa、versicolor. 每个物种分别有50个observations. 每个observations有4个变量，分别是：”Sepal.Length” 、”Sepal.Width”、 “Petal.Length” 、”Petal.Width” “Species”

virginica的频率为50，setosa的频率为50，versicolor的频率也为50. 它们三个物种的相对频率都为50 / 150 = 1/3. 所有物种相对频率的和为1.

下面我用ggplot来画出histogram(直方图)和bar chart(条形图)

library(ggplot2)
library(gridExtra)

p1 <- ggplot(data = iris, aes(x = Species, fill = Species)) + 
  geom_bar() + 
  labs(list(title = "频率演示", x = "物种", y = "物种频率"))

p2 <- ggplot(data = iris, aes(x = Species, y = 1 / length(iris$Species))) + 
  geom_bar(stat = "identity", aes(fill = Species)) + 
  labs(list(title = "相对频率演示", x = "物种", y = "物种相对频率"))

grid.arrange(p1, p2)

ggplot(data = iris, aes(x = Petal.Length)) + 
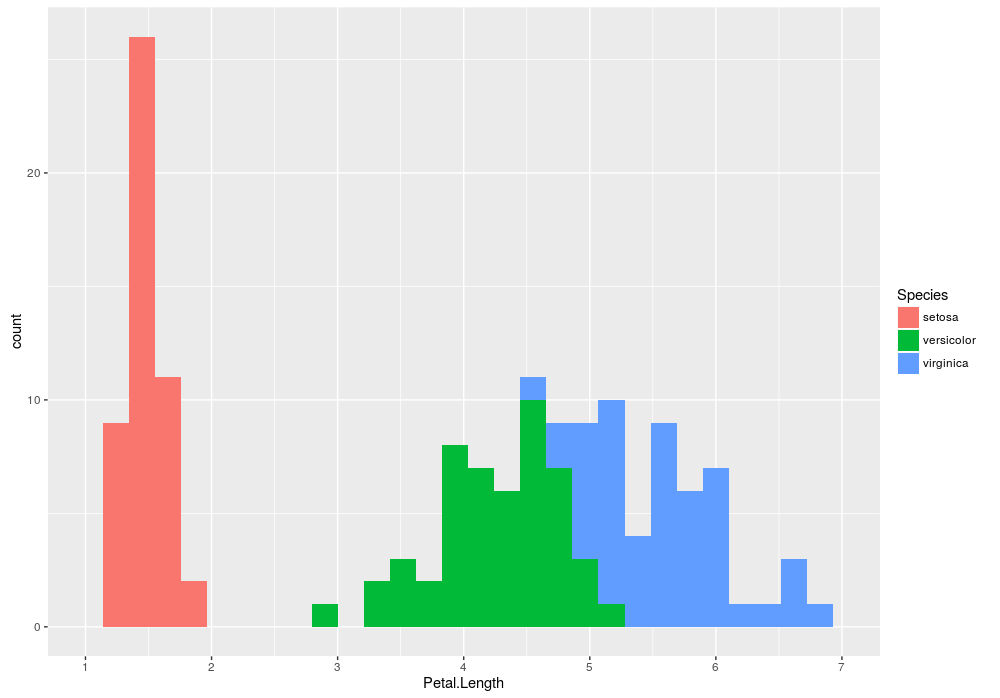
  geom_histogram(aes(fill = Species)) +
  scale_x_continuous(limits = c(1, 7), breaks = seq(1, 7, 1))

直方图的x-axis是Numerical/Quantitative，我们可以从中看到某个变量的分布情况。条形图的x-axis是Categoriacla/Qualitative，我们可以看到某个类别的总数。如果你想了解更多的信息，请参考：histogram(直方图)和bar chart(条形图)

直方图的区间(interval <=> bin <=> bucket)并不是一成不变的，我们可以根据具体的应用来调整。如果你想玩玩直方图的区间，这有个交互式的网站，你可以玩玩。Interactivate Histogram

众数(mode)、平均数(Mean)和中位数(Median)

众数、平均数和中位数在某些情况下测量的都是数据的中心。下面，我们来具体看一下这三个统计学量。

假设我们从自然数population中取出2个samples，如下：

• 2,1,1,10,12,9,7,6
• 1,2,3,4,4,5,6,7,8

上面两个samples的众数分别是：1和4

1. 如果我在上面两个samples中分别加上一个自然数1999999999，众数依然保持不变，它并没有受到异常值影响。
2. 从同一个population中取出的sample，众数并不相接近
3. 第2个sample的众数代表着数据的中心，而第一个没有

---

下面两个公式分别计算的是sample和population的平均数。

x¯=∑ni=1xinμ=