【Apollo7.0】感知模块(4):激光雷达感知中的目标跟踪算法—具体技术细节
Track流程与目的
目标跟踪的主要目的是:根据运动目标相关的特征值,将障碍物序列中连续帧的同一运动目标关联起,得到每帧数据中目标的运动参数以及相邻帧间目标的对应关系,从而得到障碍物完整的运动轨迹。
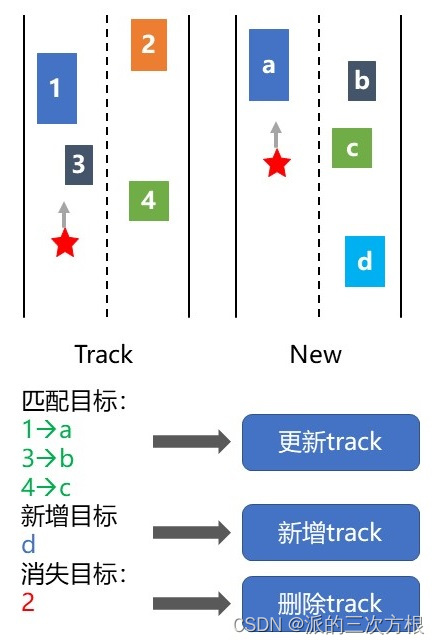
匈牙利匹配
匈牙利匹配法是一个二分图匹配算法,由匈牙利数学家Edmonds于1965年提出,因而得名。
二分图匹配:Bipartite Graph Matching
具体细节可以从参考以下链接:
Apollo perception源码阅读|fusion之匈牙利算法
算法流程
现在我们要进行跟踪目标与新点云目标之间的匹配,下面进行简单的示意图理解。
Step 1: 初始构成
由下图所示,
Track中的目标1与New中的目标1、2可以进行匹配;
Track中的目标2与New中的目标2、3可以进行匹配;
Track中的目标3与New中的目标1、2可以进行匹配;
Track中的目标4与New中的目标3可以进行匹配。
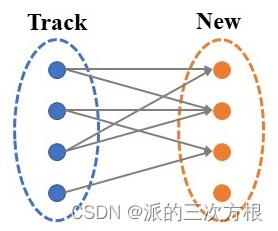
Step 2: Track中的目标1进行匹配
Track中的目标1与New中目标1形成匹配。
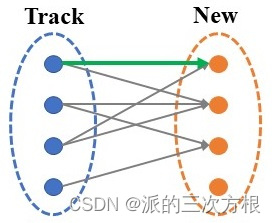
Step 3: Track中的目标2进行匹配
Track中的目标2与New中目标2形成匹配。
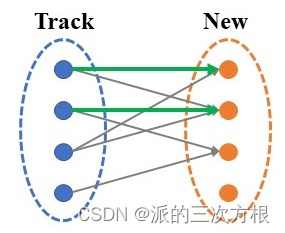
Step 4: Track中的目标3进行匹配
Track中的目标3与New中目标1、2可以进行匹配,但New中目标1、2均被占据,因此需要将先前的匹配重新调整。
首先,取消Track目标1形成的匹配,如下图所示,
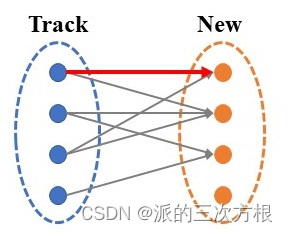
Track目标1取消匹配后,需要重新进行匹配,能够匹配的只有New中目标2,但New目标2被Track目标2所占据,
因此需要再次取消Track目标2的匹配。
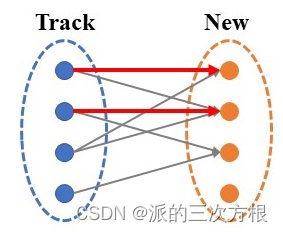
Track目标2取消匹配后,建立与New中目标3的匹配;此时,Track目标1可以建立与New目标2的匹配;
最终,Track目标3与New目标1形成匹配;因此,Track目标1、2、3都找到了对应的匹配。
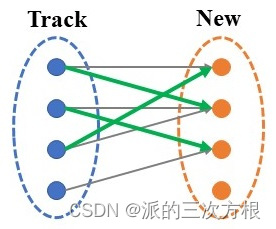
Step 5:Track中的目标4进行匹配
Track目标4只能与New目标3形成匹配,因此需要重新调整先前的匹配。但是,按照上面的调整逻辑,始终无法为Track目标4调整出一个空闲目标。因此,Track目标4无法进行匹配,表明该目标已消失。
对于New中目标4,其在Track中无对应匹配,表明该目标是一个新目标。
算法局限性
匈牙利匹配目的在于实现两个集合之间的最大匹配,为了防止误匹配,要求两个集合中的关联度足够准确。
关联矩阵计算 (association_mat)
关联矩阵包含跟踪目标与新点云目标两两之间的距离值。
该距离是通过计算7种特征距离得来的,分别是
- 定位距离
- 朝向距离
- bbox尺寸距离
- 目标点数距离
- 直方图距离
- 重心距离
- bbox IoU距离
因为每种特征距离的误差与不确定性是不同的,所以需要赋予每种特征距离一定的权重系数:
- 前景距离权重
kForegroundDefaultWeight = {0.6f, 0.2f, 0.1f, 0.1f, 0.5f, 0.f, 0.f} - 后景距离权重
kBackgroundDefaultWeight = {0.f, 0.f, 0.f, 0.f, 0.f, 0.2f, 0.8f}
可以看出前景目标匹配中,定位距离、朝向距离、直方图距离是主要因素。
笔者认为该权重系数应该没有理论依据,是通过大量实验及经验确定的。
跟踪目标位置预测
新点云目标必然是超前与跟踪目标的,为了实现精准匹配,需要依据点云目标的时间戳,对跟踪目标的位置进行预测。
void MlfTrackData::PredictState(double timestamp) const {
if (history_objects_.empty()) {
return;
}
// 跟踪目标中最新的历史目标
auto latest_iter = history_objects_.rbegin();
// 最新跟踪目标的时间戳
const double latest_time = latest_iter->first;
// 最新跟踪目标
const auto& latest_object = latest_iter->second;
// 与点云目标的时间差
double time_diff = timestamp - latest_time;
// 最新跟踪目标的位置
const Eigen::Vector3d& latest_anchor_point =
latest_object->belief_anchor_point;
// 最新跟踪目标的速度
const Eigen::Vector3d& latest_velocity = latest_object->output_velocity;
// 预测量
predict_.state.resize(6);
// 位置:x、y、z
predict_.state(0) = static_cast<float>(latest_anchor_point(0) +
latest_velocity(0) * time_diff);
predict_.state(1) = static_cast<float>(latest_anchor_point(1) +
latest_velocity(1) * time_diff);
predict_.state(2) = static_cast<float>(latest_anchor_point(2) +
latest_velocity(2) * time_diff);
// 速度:vx、vy、vz
predict_.state(3) = static_cast<float>(latest_velocity(0));
predict_.state(4) = static_cast<float>(latest_velocity(1));
predict_.state(5) = static_cast<float>(latest_velocity(2));
// 时间戳
predict_.timestamp = timestamp;
// TODO(.): predict cloud and polygon if needed in future.
}
1. 定位距离
定位距离通常计算的是xoy平面内的距离。
记,跟踪目标的 预测位置为
(
x
p
,
y
p
)
(x_p,y_p)
(xp,yp),新目标位置为
(
x
n
,
y
n
)
(x_n,y_n)
(xn,yn), 跟踪目标的速度为
(
v
x
,
v
y
)
(v_x,v_y)
(vx,vy)
低速情况下:
定位距离可以直接使用欧式距离,
$
l
o
c
a
l
t
i
o
n
_
d
i
s
t
=
(
x
p
−
x
n
)
2
+
(
y
p
−
y
n
)
2
localtion\_dist=\sqrt{(x_p-x_n)^2+(y_p-y_n)^2}
localtion_dist=(xp−xn)2+(yp−yn)2
速度较快时:
定位距离利用正态分布进行估计,apollo将速度阈值设为2。
计算速度
v
=
v
x
2
+
v
y
2
v=\sqrt{v_x^2+v_y^2}
v=vx2+vy2,速度向量进行单位化,得到
(
v
x
i
,
v
y
i
)
(v_{xi},v_{yi})
(vxi,vyi)。
[ d x d y ] = [ v x i v y i v y i − v x i ] [ x p − x n y p − y n ] \begin{bmatrix}d_x \\ d_y\end{bmatrix}=\begin{bmatrix} v_{xi} & v_{yi} \\ v_{yi} & -v_{xi} \end{bmatrix}\begin{bmatrix} x_p-x_n \\ y_p-y_n \end{bmatrix} [dxdy]=[vxivyivyi−vxi][xp−xnyp−yn], l o c a l t i o n _ d i s t = d x 2 ∗ 0.5 + d y 2 ∗ 2 localtion\_dist=\sqrt{d_x^2*0.5+d_y^2*2} localtion_dist=dx2∗0.5+dy2∗2
2. 朝向距离
取值范围:
(
0
,
2
)
(0,2)
(0,2)
d
i
r
e
c
t
i
o
n
_
d
i
s
t
=
1
−
v
x
d
x
+
v
y
d
y
v
x
2
+
v
y
2
(
x
p
−
x
n
)
2
+
(
y
p
−
y
n
)
2
direction\_dist=1-\dfrac{v_xd_x+v_yd_y}{\sqrt{v_x^2+v_y^2}\sqrt{(x_p-x_n)^2+(y_p-y_n)^2}}
direction_dist=1−vx2+vy2(xp−xn)2+(yp−yn)2vxdx+vydy
3. bbox尺寸距离
取值范围:
(
0
,
1
)
(0,1)
(0,1)
记,跟踪目标bbox平面内的方向与尺寸分别为
(
d
i
r
x
t
,
d
i
r
y
t
)
(dir_{xt},dir_{yt})
(dirxt,diryt),
(
s
i
z
e
x
t
,
s
i
z
e
y
t
)
(size_{xt},size_{yt})
(sizext,sizeyt),
点云目标bbox平面内的方向与尺寸分别为
(
d
i
r
x
n
,
d
i
r
y
n
)
(dir_{xn},dir_{yn})
(dirxn,diryn),
(
s
i
z
e
x
n
,
s
i
z
e
y
n
)
(size_{xn},size_{yn})
(sizexn,sizeyn)。
[ d 1 d 2 ] = [ d i r x t d i r y t − d i r y t d i r x t ] [ s i z e x n s i z e y n ] \begin{bmatrix} d_1 \\ d_2 \end{bmatrix}=\begin{bmatrix} dir_{xt} & dir_{yt} \\ -dir_{yt} & dir_{xt} \end{bmatrix} \begin{bmatrix} size_{xn} \\ size_{yn} \end{bmatrix} [d1d2]=[dirxt−dirytdirytdirxt][sizexnsizeyn]
若 ∣ a ∣ > ∣ b ∣ |{a}|>|{b}| ∣a∣>∣b∣,
t
1
=
s
i
z
e
x
t
−
s
i
z
e
x
n
m
a
x
(
s
i
z
e
x
t
,
s
i
z
e
x
n
)
t_1=\dfrac{size_{xt}-size_{xn}}{max(size_{xt},size_{xn})}
t1=max(sizext,sizexn)sizext−sizexn,
t
2
=
s
i
z
e
y
t
−
s
i
z
e
y
n
m
a
x
(
s
i
z
e
y
t
,
s
i
z
e
y
n
)
t_2=\dfrac{size_{yt}-size_{yn}}{max(size_{yt},size_{yn})}
t2=max(sizeyt,sizeyn)sizeyt−sizeyn
b
b
o
x
_
s
i
z
e
_
d
i
s
t
=
m
i
n
(
∣
t
1
∣
,
∣
t
2
∣
)
bbox\_size\_dist=min(|t_1|,|t_2|)
bbox_size_dist=min(∣t1∣,∣t2∣)
若 ∣ a ∣ < = ∣ b ∣ |{a}|<=|{b}| ∣a∣<=∣b∣,
t 1 = s i z e x t − s i z e y n m a x ( s i z e x t , s i z e y n ) t_1=\dfrac{size_{xt}-size_{yn}}{max(size_{xt},size_{yn})} t1=max(sizext,sizeyn)sizext−sizeyn, t 2 = s i z e y t − s i z e x n m a x ( s i z e y t , s i z e x n ) t_2=\dfrac{size_{yt}-size_{xn}}{max(size_{yt},size_{xn})} t2=max(sizeyt,sizexn)sizeyt−sizexn
b b o x _ s i z e _ d i s t = m i n ( ∣ t 1 ∣ , ∣ t 2 ∣ ) bbox\_size\_dist=min(|t_1|,|t_2|) bbox_size_dist=min(∣t1∣,∣t2∣)
4. 目标点数距离
取值范围:
(
0
,
1
)
(0,1)
(0,1)
记,跟踪目标的点数为
n
u
m
t
num_t
numt,点云目标的点数为
n
u
m
n
num_n
numn
p o i n t _ n u m _ d i s t = ∣ n u m t − n u m n ∣ m a x ( n u m t , n u m n ) point\_num\_dist=\dfrac{|num_t-num_n|}{max(num_t,num_n)} point_num_dist=max(numt,numn)∣numt−numn∣
5. 直方图距离
取值范围:
(
0
,
3
)
(0,3)
(0,3)
记,跟踪目标的直方图为
s
h
a
p
e
t
shape_t
shapet,点云目标的直方图为
s
h
a
p
e
n
shape_n
shapen
每个目标被划分为10个直方图,xyz方向共计30个直方图。
s h a p e _ d i s t = ∑ i = 0 n = 30 ∣ s h a p e t i − s h a p e n i ∣ shape\_dist=\displaystyle\sum_{i=0}^{n=30}|shape_{ti}-shape_{ni}| shape_dist=i=0∑n=30∣shapeti−shapeni∣
6. 重心距离
记,跟踪目标的重心为 ( c x t , c y t ) (c_{xt},c_{yt}) (cxt,cyt),点云目标的重心为 ( c x n , c y n ) (c_{xn},c_{yn}) (cxn,cyn)
c e n t r o i d _ d i s t = ( c x t − c x n ) 2 + ( c y t − c y n ) 2 centroid\_dist=\sqrt{(c_{xt}-c_{xn})^2+(c_{yt}-c_{yn})^2} centroid_dist=(cxt−cxn)2+(cyt−cyn)2
7. bbox IoU距离
首先获取跟踪目标与点云目标bbox的方向、尺寸、中心点;
比较跟踪目标与点云目标包含的点数;
谁的点数少,就修正谁。
如,跟踪目标点云少,
令跟踪目标方向等于点云目标方向,重新计算跟踪目标bbox的尺寸与中心点。
依据跟踪目标的bbox方向构成二维变换矩阵,对跟踪目标与点云目标的中心点进行变换;
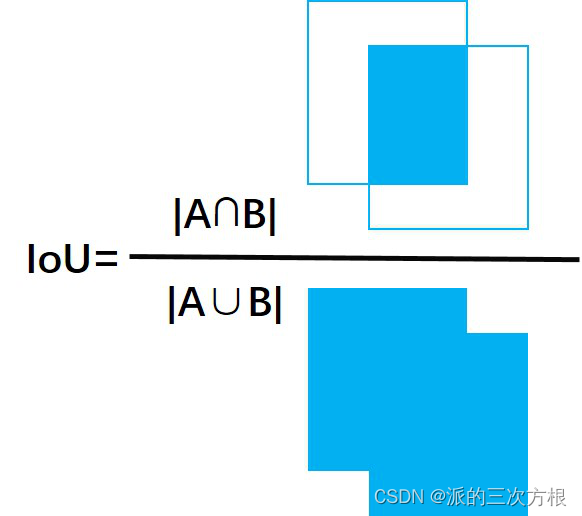
根据跟踪目标与点云目标的中心点、尺寸,计算两者的IoU
I
o
U
_
d
i
s
t
=
(
1
−
I
o
U
)
∗
m
a
t
c
h
_
t
h
r
e
s
h
o
l
d
IoU\_dist=(1-IoU)*match\_threshold
IoU_dist=(1−IoU)∗match_threshold
m
a
t
c
h
_
t
h
r
e
s
h
o
l
d
=
4.0
match\_threshold=4.0
match_threshold=4.0
IoU: Intersection over Union,两个检测框的交集与并集的比值
卡尔曼滤波
该过程主要用MlfMotionFilter估计跟踪目标的运动速度,所使用到的主要算法为卡尔曼滤波。
原理示意图(参考自apollo星火计划学习笔记)

卡尔曼滤波是一种基于最优估计的滤波算法,通过综合考虑预测值与测量值,迭代出具有最小不确定性的状态估计。
卡尔曼滤波适用于任何线性系统,对于非线性系统,可以使用扩展卡尔曼滤波(EKF)。
卡尔曼滤波会用到两个状态值,
- 预测值
- 测量值
预测值是通过状态方程与时间差,利用上一时刻的状态对当前状态进行预测。
测量值是传感器测量得到的数据。
最优状态估计值是通过预测值与测量值加权平均得到的:
估计值 = 预测值 + K * (测量值-预测值)
其中,K称为卡尔曼增益
核心思想
假定观测的系统是线性的,噪声都满足高斯分布。
当前时刻系统的最优状态估计,是当前时刻系统的预测值和当前时刻系统的测量值的加权平均。得到最优估计之后,再将最优估计和预测值进行对比。如果相差比较小,则说明预测值比较准确,下一时刻进行状态估计时就加大预测值的权值;反之,说明预测值不准确,下一时刻进行状态估计时就加大测量值的权值。权值的计算就是不断更新卡尔曼增益的过程。
公式表达
预测方程:
X t = F t X t − 1 + B t U t {\bf{X}}_t={\bf{F}}_t{\bf{X}}_{t-1}+{\bf{B}}_t{\bf{U}}_t Xt=FtXt−1+BtUt
X
t
{\bf{X}}_t
Xt为状态预测值
F
t
{\bf{F}}_t
Ft为状态变换矩阵,如运动学方程中的变换矩阵
U
t
{\bf{U}}_t
Ut为控制向量,如驱动电机带来的加速度
B
t
{\bf{B}}_t
Bt为控制矩阵,变换控制变量为状态的矩阵
观测方程:
Z t = H X t {\bf{Z}}_t={\bf{H}}{\bf{X}}_{t} Zt=HXt
Z
t
{\bf{Z}}_t
Zt为传感器测量值。
H
{\bf{H}}
H为状态与测量值之间的变换矩阵。
传感器测量值与状态可能不是一种量,如激光测距仪测量的是光的飞行时间,而所需的状态值是距离,就需要一个变换矩阵
H
{\bf{H}}
H将其进行转换。如果传感器能直接测量状态,则
H
{\bf{H}}
H为单位阵。
在真实环境下,预测值与测量值具有不确定性,均带有误差,即噪声,
X
t
=
F
t
X
t
−
1
+
B
t
U
t
+
W
{\bf{X}}_t={\bf{F}}_t{\bf{X}}_{t-1}+{\bf{B}}_t{\bf{U}}_t+{\bf{W}}
Xt=FtXt−1+BtUt+W
Z
t
=
H
X
t
+
V
{\bf{Z}}_t={\bf{H}}{\bf{X}}_{t}+{\bf{V}}
Zt=HXt+V
W
{\bf{W}}
W为预测噪声,
V
{\bf{V}}
V为测量噪声,均满足高斯分布,
W
∼
N
(
0
,
Q
)
{\bf{W}}\thicksim{N(0,{\bf{Q}})}
W∼N(0,Q)
V
∼
N
(
0
,
R
)
{\bf{V}}\thicksim{N(0,{\bf{R}})}
V∼N(0,R)为了衡量状态估计值的不确定性,引入协方差矩阵。
预测值的协方差矩阵,
P
t
=
F
t
P
t
−
1
F
t
T
+
Q
t
{\bf{P}}_t={\bf{F}}_t{\bf{P}}_{t-1}{\bf{F}}_t^T+{\bf{Q}}_t
Pt=FtPt−1FtT+Qt预测值的不确定性,一部分来自于上一时刻的估计值,其本身就带有不确定性
P
t
−
1
{\bf{P}}_{t-1}
Pt−1,另一部分来源于本次估计引入的新噪声
Q
t
{\bf{Q}}_t
Qt。
测量值的不确定性来源于通常是固定参数— R \bf{R} R,有传感器的测量方差所确定。
最优估计
由上可知,卡尔曼滤波的最优估计为,
X
t
^
=
X
t
+
K
t
(
Z
t
−
H
X
t
)
\hat{{\bf{X}}_t}={\bf{X}}_t+{\bf{K}}_t({\bf{Z}}_t-{\bf{H}}{\bf{X}}_t)
Xt^=Xt+Kt(Zt−HXt)卡尔曼增益为,
K
t
=
P
t
H
T
H
P
t
H
T
+
R
t
{\bf{K}}_t=\dfrac{{\bf{P}}_t{\bf{H}}^T}{{\bf{H}}{\bf{P}}_t{\bf{H}}^T+{\bf{R}}_t}
Kt=HPtHT+RtPtHT最优估计的协方差矩阵为,
P
t
^
=
(
I
−
K
t
H
)
P
t
\hat{{\bf{P}}_t}=(\bf{I}-{\bf{K}}_t{\bf{H}}){\bf{P}}_t
Pt^=(I−KtH)Pt关于公式的推导,请参考,
【工程师学算法】工程常用算法(二)—— 卡尔曼滤波(Kalman Filter
Apollo学习笔记(17)卡尔曼滤波
详解卡尔曼滤波原理
卡尔曼滤波流程
卡尔曼滤波流程总结为以下五步:
计算当前时刻的预测值,
X
t
=
F
t
X
^
t
−
1
+
B
t
U
t
{\bf{X}}_t={\bf{F}}_t\hat{\bf{X}}_{t-1}+{\bf{B}}_t{\bf{U}}_t
Xt=FtX^t−1+BtUt计算预测值的协方差矩阵,
P
t
=
F
t
P
t
−
1
F
t
T
+
Q
t
{\bf{P}}_t={\bf{F}}_t{\bf{P}}_{t-1}{\bf{F}}_t^T+{\bf{Q}}_t
Pt=FtPt−1FtT+Qt计算卡尔曼增益,
K
t
=
P
t
H
T
H
P
t
H
T
+
R
t
{\bf{K}}_t=\dfrac{{\bf{P}}_t{\bf{H}}^T}{{\bf{H}}{\bf{P}}_t{\bf{H}}^T+{\bf{R}}_t}
Kt=HPtHT+RtPtHT计算最优状态估计,
X
t
^
=
X
t
+
K
t
(
Z
t
−
H
X
t
)
\hat{{\bf{X}}_t}={\bf{X}}_t+{\bf{K}}_t({\bf{Z}}_t-{\bf{H}}{\bf{X}}_t)
Xt^=Xt+Kt(Zt−HXt)计算最优估计的协方差矩阵,
P
t
^
=
(
I
−
K
t
H
)
P
t
\hat{{\bf{P}}_t}=(\bf{I}-{\bf{K}}_t{\bf{H}}){\bf{P}}_t
Pt^=(I−KtH)Pt
其中,
X
^
t
\hat{\bf{X}}_{t}
X^t:t时刻的最优估计,需要计算,最终输出1
P
^
t
\hat{\bf{P}}_{t}
P^t:t时刻最优估计的协方差矩阵,需要计算,最终输出2
X
^
t
−
1
\hat{\bf{X}}_{t-1}
X^t−1:t-1时刻的最优估计
P
^
t
−
1
\hat{\bf{P}}_{t-1}
P^t−1:t-1时刻最优估计的协方差矩阵
X
t
{\bf{X}}_{t}
Xt:t时刻的预测值,需要计算,由t-1时刻的最优估计计算得到
Z
t
{\bf{Z}}_{t}
Zt:t时刻的测量值,由传感器进行输出
F
t
{\bf{F}}_{t}
Ft:t时刻的状态变换矩阵,由公式得来
U
t
{\bf{U}}_{t}
Ut:t时刻系统的控制输入向量
B
t
{\bf{B}}_{t}
Bt:t时刻系统的控制输入矩阵
Q
t
{\bf{Q}}_{t}
Qt:t时刻预测值的外部噪声,需要计算或者人工设置
R
t
{\bf{R}}_{t}
Rt:t时刻测量值的观测噪声,需要计算或者从传感器指导手册中获得
H
{\bf{H}}
H:真实状态与测量值的变换矩阵,通常为固定形式
K
t
{\bf{K}}_{t}
Kt:t时刻的卡尔曼增益,需要计算
apollo代码解释
关于运动估计与滤波这一部分代码为MlfMotionFilter
关于测量值ComputeMotionMeasurment
apollo中计算了三种测量值:点云中心速度、点云bbox中心速度、点云bbox角点速度
冗余观测将为滤波测量带来额外的鲁棒性, 因为所有观察失败的概率远远小于单次观察失败的概率。
apollo技术文档—3D障碍物感知
void MlfMotionMeasurement::ComputeMotionMeasurment(
const MlfTrackDataConstPtr& track_data, TrackedObjectPtr new_object) {
// prefer to choose objects from the same sensor
std::string sensor_name = new_object->sensor_info.name;
TrackedObjectConstPtr latest_object =
track_data->GetLatestSensorObject(sensor_name).second;
if (latest_object == nullptr) {
latest_object = track_data->GetLatestObject().second;
}
if (latest_object.get() == nullptr) {
AERROR << "latest_object is not available";
return;
}
// should we estimate the measurement if the time diff is too small?
double latest_time = latest_object->object_ptr->latest_tracked_time;
double current_time = new_object->object_ptr->latest_tracked_time;
double time_diff = current_time - latest_time;
if (fabs(time_diff) < EPSILON_TIME) {
time_diff = DEFAULT_FPS;
}
// 点云重心的速度测量值
MeasureAnchorPointVelocity(new_object, latest_object, time_diff);
// 点云bbox的中心速度测量值
MeasureBboxCenterVelocity(new_object, latest_object, time_diff);
// 点云bbox的角点速度测量值
MeasureBboxCornerVelocity(new_object, latest_object, time_diff);
// 测量值的选择:依据运动一致性,决定上述三种速度用于滤波的选择
MeasurementSelection(track_data, latest_object, new_object);
// 测量值的质量估计
MeasurementQualityEstimation(latest_object, new_object);
}
卡尔曼滤波KalmanFilterUpdateWithPartialObservation
这个函数的整个过程与卡尔曼滤波五步过程是对应的。
获取上一时刻的状态及其协方差,状态是一个4维向量
[
v
x
v
y
a
x
a
y
]
T
\begin{bmatrix} v_x & v_y & a_x & a_y \end{bmatrix}^T
[vxvyaxay]T,
// 上一时刻的状态:两个方向的速度与加速度,vx,vy,ax,ay
const Eigen::Vector4d& last_state = latest_object->state;
// 上一时刻状态的协方差
const Eigen::Matrix4d& last_state_covariance =
latest_object->state_covariance;
根据时间差与方向变化,计算状态变换矩阵,
// 时间差
double time_diff = new_object->object_ptr->latest_tracked_time -
latest_object->object_ptr->latest_tracked_time;
if (time_diff < EPSION_TIME) { // Very small time than assign
time_diff = DEFAULT_FPS;
}
// 状态变换矩阵:v(t)=v(t-1)+dt*a(t-1)
Eigen::Matrix4d transition = Eigen::Matrix4d::Identity();
transition(0, 2) = transition(1, 3) = time_diff;
// composition with rotation
// 根据方向的旋转进行分解
if (new_object->type != base::ObjectType::PEDESTRIAN &&
range < trust_orientation_range_) {
Eigen::Vector2d cur_dir = new_object->direction.head<2>();
Eigen::Vector2d pre_dir = latest_object->direction.head<2>();
cur_dir.normalize();
pre_dir.normalize();
double cos_theta = cur_dir.dot(pre_dir);
double sin_theta = pre_dir(0) * cur_dir(1) - pre_dir(1) * cur_dir(0);
Eigen::Matrix2d rot;
rot << cos_theta, -sin_theta, sin_theta, cos_theta;
Eigen::Matrix4d rot_extend = Eigen::Matrix4d::Zero();
rot_extend.block<2, 2>(0, 0) = rot;
rot_extend.block<2, 2>(2, 2) = rot;
transition = rot_extend * transition;
}
获得当前时刻状态及其协方差的引用,
// 当前时刻的状态,下面就是对其进行计算
auto& state = new_object->state;
// 当前时刻状态的协方差
auto& state_covariance = new_object->state_covariance;
auto measurement_covariance =
new_object->measurement_covariance.block<2, 2>(0, 0);
计算预测值的外部噪声的协方差,实际上是给定一个系数(50),然后乘上时间差的平方,
// 预测值
state = transition * last_state;
// 预测值的协方差
state_covariance =
transition * last_state_covariance * transition.transpose() +
predict_covariance;
获得测量值,计算测量值的协方差矩阵,
// 2. measurement update stage
// 测量值
Eigen::Vector2d measurement;
measurement << new_object->selected_measured_velocity.head<2>();
// 计算测量值的协方差
Eigen::Vector2d direction = new_object->direction.head<2>();
direction.normalize();
Eigen::Vector2d odirection(direction(1), -direction(0));
if (new_object->type == base::ObjectType::PEDESTRIAN &&
range < trust_orientation_range_) {
measurement_covariance = Eigen::Matrix2d::Identity();
measurement_covariance *= measured_velocity_variance_;
} else {
const double kVarianceAmplifier = 9.0;
measurement_covariance =
measured_velocity_variance_ * direction * direction.transpose() +
(measured_velocity_variance_ +
fabs(measurement.dot(odirection)) * kVarianceAmplifier) *
odirection * odirection.transpose();
}
确定真实状态与测量值的变换矩阵,这里测量值就是速度,因此前一部分就是单位阵,关于加速度的那一部分直接赋值为0,
// 真实状态与测量值的变换矩阵,这里测量值直接反映了状态,因此变换矩阵为单位阵
Eigen::Matrix<double, 2, 4> observation_transform;
observation_transform.block<2, 2>(0, 0).setIdentity();
observation_transform.block<2, 2>(0, 2).setZero();
计算卡尔曼增益,直接对照公式就可以,
// 卡尔曼增益矩阵
Eigen::Matrix<double, 4, 2> kalman_gain_matrix =
static_cast<Eigen::Matrix<double, 4, 2, 0, 4, 2>>(
state_covariance * observation_transform.transpose() *
(observation_transform * state_covariance *
observation_transform.transpose() +
measurement_covariance)
.inverse());
计算状态增益,
// 状态增益:K*(测量值-H*预测值)
Eigen::Vector4d state_gain =
static_cast<Eigen::Matrix<double, 4, 1, 0, 4, 1>>(
kalman_gain_matrix * (measurement - observation_transform * state));
状态增益调整与后验估计,前面ComputeMotionMeasurment计算测量值的时候,进行了质量估计,这里就是通过质量系数对状态增益进行调整,同时增加增益过大限制,
// 3. gain adjustment and estimate posterior
// 状态增益调整与后验估计
// 根据测量速度的质量对增益调整,同时增加增益过大限制
StateGainAdjustment(track_data, latest_object, new_object, &state_gain);
最后,更新当前时刻的状体及其协方差,
// 最优状态估计
state = state + state_gain;
// 最优状态估计的协方差
state_covariance = (Eigen::Matrix4d::Identity() -
kalman_gain_matrix * observation_transform) *
state_covariance;
// 4. finally, state to belief and output to keep consistency
new_object->belief_velocity_gain << state_gain.head<2>(), 0;
在理解了卡尔曼滤波的理论后,再去看代码,发现这一部分的逻辑还是很清楚的。
shape滤波
采用MlfShapeFilter滤波器,融合新旧目标的shape参数,对新目标的shape参数进行修正。
shape参数包括:点云目标中心center,点云目标尺寸size,点云目标朝向direction。
Step 1:凸点检测
首先是计算更为紧凑的凸点多边形,对于前景目标,去除地面与高于车身的点,再计算目标点云的凸点。
// 重新计算凸点,去除地面与高于车身的点
hull_.GetConvexHullWithoutGroundAndHead(
obj->lidar_supplement.cloud_world,
static_cast<float>(bottom_points_ignore_threshold_),
static_cast<float>(top_points_ignore_threshold_), &obj->polygon);
其中,bottom_points_ignore_threshold_ = 0.1f,top_points_ignore_threshold_=1.6f
Step 2:方向向量估计
融合新旧目标的方向向量,重新估计目标的方向向量。
融合估计前,作了方向一致性检测,且以旧目标方向为准,若新目标方向与旧目标方向相反,就乘以-1进行校正。
然后进行加权计算,新目标权重0.6,旧目标权重0.4
// 方向不一致检测
if (new_object->direction.dot(latest_object->direction) < 0) {
new_object->direction *= -1;
}
// 方向加权计算
static const double kMovingAverage = 0.6;
new_object->direction =
latest_object->output_direction * (1 - kMovingAverage) +
new_object->direction * kMovingAverage;
new_object->direction.normalize();
Step 3:重新计算目标shape参数
将估计的方向向量赋予原始目标,然后重新计算目标shape参数。
// 替换为新方向
obj->direction = new_object->direction.cast<float>(); // sync
// finally, recompute object shape
// 在新方向下,重新计算目标shape的中心与尺寸
ComputeObjectShapeFromPolygon(obj, true);
在计算shape参数,需要将点云变换到以方向向量为基底的坐标系下,使得点云与坐标轴对齐,进而计算点云目标的长与宽。
记,方向向量为
[
d
i
r
x
d
i
r
y
]
T
\begin{bmatrix} dir_x&dir_y \end{bmatrix}^T
[dirxdiry]T,则变换公式为,
[ x ′ y ′ ] = [ d i r x d i r y − d i r y d i r x ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix}=\begin{bmatrix} dir_x&dir_y \\ -dir_y&dir_x\end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[dirx−dirydirydirx][xy]
主要代码及注释
shape滤波主要代码如下
void MlfShapeFilter::UpdateWithObject(const MlfFilterOptions& options,
const MlfTrackDataConstPtr& track_data,
TrackedObjectPtr new_object) {
// compute tight object polygon
// 计算更为紧凑的凸点多边形
auto& obj = new_object->object_ptr;
if (new_object->is_background) {
hull_.GetConvexHull(obj->lidar_supplement.cloud_world, &obj->polygon);
} else {
// 重新计算凸点,去除地面与高于车身的点
hull_.GetConvexHullWithoutGroundAndHead(
obj->lidar_supplement.cloud_world,
static_cast<float>(bottom_points_ignore_threshold_),
static_cast<float>(top_points_ignore_threshold_), &obj->polygon);
}
// simple moving average orientation filtering
// 估计目标的方向向量
if (track_data->age_ > 0) {
TrackedObjectConstPtr latest_object = track_data->GetLatestObject().second;
// 方向不一致检测
if (new_object->direction.dot(latest_object->direction) < 0) {
new_object->direction *= -1;
}
// 方向加权计算
static const double kMovingAverage = 0.6;
new_object->direction =
latest_object->output_direction * (1 - kMovingAverage) +
new_object->direction * kMovingAverage;
new_object->direction.normalize();
}
// 原始点云目标的方向、中心、尺寸
Eigen::Vector3f local_direction = obj->direction;
Eigen::Vector3d local_center = obj->center;
Eigen::Vector3f local_size = obj->size;
// 替换为新方向
obj->direction = new_object->direction.cast<float>(); // sync
// finally, recompute object shape
// 在新方向下,重新计算目标shape的中心与尺寸
ComputeObjectShapeFromPolygon(obj, true);
new_object->center = obj->center;
new_object->size = obj->size.cast<double>();
// center and size in object should not changed
// 原始目标的shape参数还原
obj->center = local_center;
obj->size = local_size;
obj->direction = local_direction;
// 新目标shape参数更新
new_object->output_center = new_object->center;
new_object->output_direction = new_object->direction;
new_object->output_size = new_object->size;
}








 本文详细介绍了Apollo7.0激光雷达感知模块中的目标跟踪算法,包括匈牙利匹配算法的步骤、局限性和关联矩阵计算,以及卡尔曼滤波和shape滤波在目标跟踪中的应用。通过这些技术,实现对激光雷达数据中运动目标的精确匹配和跟踪,确保自动驾驶系统的障碍物识别准确性。
本文详细介绍了Apollo7.0激光雷达感知模块中的目标跟踪算法,包括匈牙利匹配算法的步骤、局限性和关联矩阵计算,以及卡尔曼滤波和shape滤波在目标跟踪中的应用。通过这些技术,实现对激光雷达数据中运动目标的精确匹配和跟踪,确保自动驾驶系统的障碍物识别准确性。
















 4878
4878

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








