（一）特征值
如果一个非零向量v是方阵A的特征向量，将一定可以表示成下面形式，而λ是特征向量v对应的特征值：
特征值分解是将一个矩阵分解成下面的形式：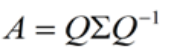
其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。一个矩阵的一组特征向量是一组正交向量。
【练习题】求解矩阵A的特征值与特征向量。
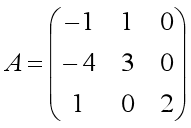
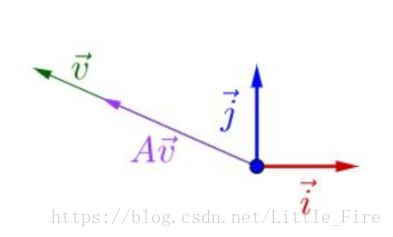
方阵的特征值表示什么含义呢，我们通过一组向量图表示。初始状态下，i（红色）和j（蓝色）表示二维坐标平面下的两个单位向量，v是空间上任意一条向量（绿色）
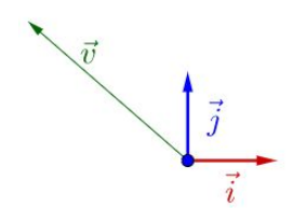
用方阵A左乘向量v之后，得到一个新的向量Av（紫色）
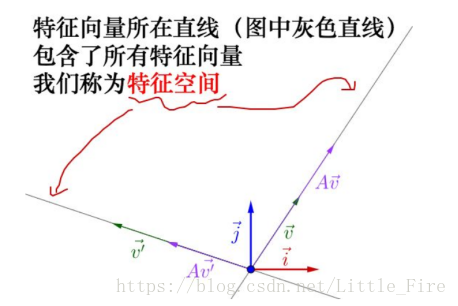
接下来，在二维空间上，手动移动向量v，移动到某一时刻，向量v（绿色）与向量Av（紫色）发生了重合，且Av的向量摸大于v的模（下图左），再继续移动v，又会发现在v与Av的另一个重合时刻，但此时|Av|<|v|（下图右）
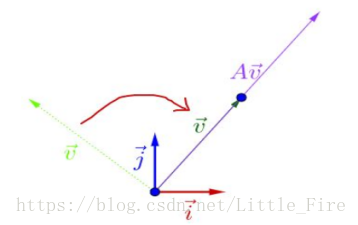
这两个时刻，v与Av发生了重合，即两个向量方向一致，大小差了一个lambda倍，也就是上面所提到的
这里的lambda就是特征值（两个特征值，一个大于1，一个小于1），这两个时刻对应的v向量，就是矩阵A的特征向量
特征值存在以下几个性质：
设n阶矩阵A=(aij) 的特征值为λ1,λ2,...λn
（1）λ1+λ2+...+λn = a11+ a22+…+ann，trail(A)=特征值的和。
（2）λ1λ2… λn =|A|，特征值的乘积=A的行列式
若λ是方阵A的特征值
（1）λ^2是A^2的特征值
（2）A可逆时，λ^(-1)是A^(-1)的特征值
（3）kλ是kA的特征值，k∈R。
设方阵A的m个特征值λ1,λ2 ,...,λm，与之对应的特征向量是p1,p2,...,pm，若λ1,λ2 ,...,λm各不相等，则p1,p2 ,...,pm线性无关。（不同特征值对应的特征向量线性无关），实对称矩阵不同特征值的特征向量相互正交。
（二）特征值分解
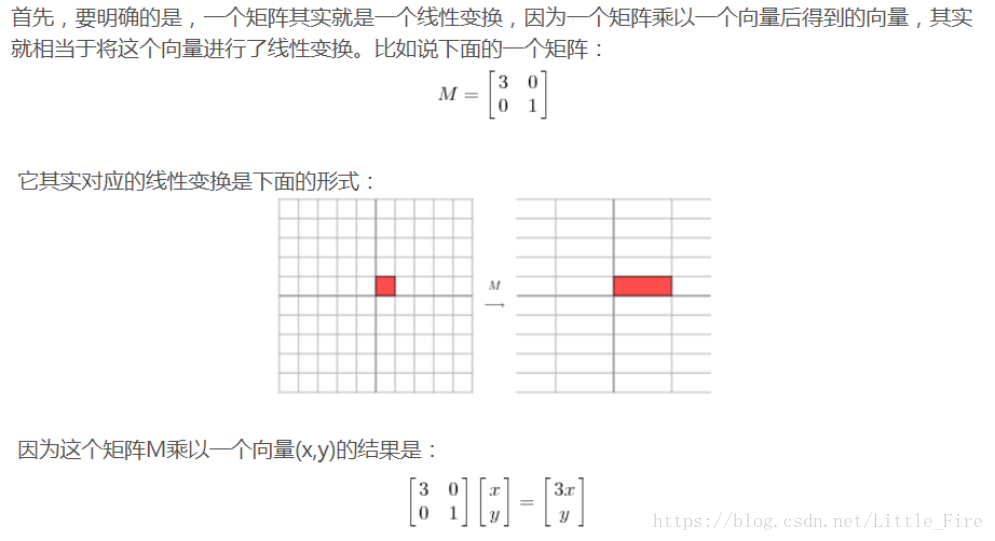
【注】因为矩阵M是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换
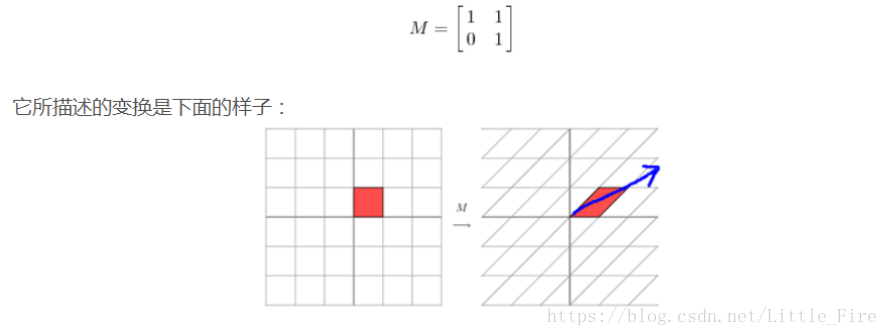
当M非对称时，在平面上对一个轴进行的拉伸变换（蓝色箭头所示）。如果要描述好一个变换M，那就描述好这个变换主要的变化方向。
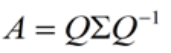
分解得到的Σ矩阵是一个对角阵，若Σ里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要变化到次要变化排列）
当矩阵是高维的情况下，那么这个矩阵A就是高维空间下的一个线性变换，这个变换也同样有很多的变换方向，通过特征值分解得到的前N个特征向量，对应了矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。
也就是说：提取这个矩阵最重要的特征。
特征值分解的局限：变换的矩阵必须是方阵！！
（三）奇异值与奇异值分解
在现实的世界中，遇到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩；有N个用户，每个用户购买了M件商品，这样形成的一个N * M的长方形矩阵。
怎样描述这样普通的矩阵的重要特征？
可以使用奇异值分解来解决
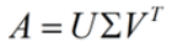
A是一个N * M的矩阵，那么得到的U是一个N * N的方阵（里面的向量是正交的，称为左奇异向量），Σ是一个N * M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），VT是一个N * N的矩阵（里面的向量也是正交的，称为右奇异向量）
右奇异向量求解：矩阵A左乘转置AT，将会得到一个方阵（m*m），我们用这个方阵求特征值和特征向量，得到的vi就是右奇异向量
根据上面得到的特征值λ，计算奇异值σ，以及左奇异向量u。
【练习题】 求解A的奇异值
可以使用Python编程实现，numpy包中存有直接计算奇异值的方法np.linalg.svd(matrix)，实例如下：
奇异值σ与特征值类似，矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解，这里r是一个远小于m、n的数。
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵。而这三个矩阵的“面积”之和要远小于原始的矩阵A，可以压缩空间来表示原矩阵A，只存储三个矩阵U、Σ、V即可。
7840
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
