论文笔记 Deep Gaussian Processes for Calibration of Computer Models 用于校准计算机模型的深度高斯过程

0.摘要

黑盒计算机模型的贝叶斯校准为量化模型参数和预测的不确定性提供了一个既定的框架。传统的贝叶斯校准涉及计算机模型的仿真和使用高斯过程的加性模型差异项；然后使用马尔可夫链蒙特卡罗进行推理。这种校准方法受到高斯过程的可扩展性差以及需要指定合理的协方差函数来处理计算机模型的复杂性和差异的限制。在这项工作中，我们提出了一个新的校准框架，通过将高斯过程组合成深度高斯过程和可扩展的变分推理技术来解决这些挑战。由于这个公式，有可能获得一种灵活的校准方法，该方法很容易在具有自动微分和利用 GPU 类型硬件的开发环境中实现。我们展示了我们的提议如何通过对各种校准问题的实验验证来产生最先进的强大替代方案。我们通过展示我们如何进行自适应实验设计并讨论所提出的校准模型的可识别性来结束本文。
关键词：贝叶斯推理，神经网络，计算机实验，深度高斯过程。

1.介绍

从数据中推断昂贵计算机模型的参数的任务是统计学中的一个经典问题（Sacks 等人，1989 年）。这样的问题被称为校准（Kennedy 和 O’Hagan，2001 年），结果通常有助于得出对物理量有直接解释的参数的结论（例如，参见 Brynjarsd´ottir 的第 2.2 节和奥哈根 2014）。校准在气候学 (Sans´o et al., 2008; Salter et al., 2018)、环境科学 (Larssen et al., 2006; Arhonditsis et al., 2007)、生物学 ( Henderson 等人，2009 年）和机械工程（Williams 等人，2006 年）等等。

校准昂贵的计算机模型存在许多基本困难，我们可以区分计算模型和统计模型。计算问题源于传统的优化和推理技术需要针对不同的参数值多次运行昂贵的计算机模型，这在给定的计算预算内可能是不可行的。相反，统计限制源于计算机模型只能以给定的准确度抽象出真实过程。

基于 Sacks 等人的先前工作。 (1989)，在他们的开创性论文中，Kennedy 和 O’Hagan (2001) 提出了一个基于高斯过程 (gps; Rasmussen and Williams 2006) 的统计模型，它共同解决了上述问题。在他们的模型中，我们将其称为 $KOH$模型，确定性计算机模型的输出是通过一组计算机实验估计的 $gp$ 来模拟的。通过这种方式，通过使用模拟 $gp$ 对任何给定参数集的预测分布来代替昂贵的计算机模型运行，绕过了计算问题。相反，来自真实过程的观察，也称为现场观察，是通过 gp 模拟计算机模型并添加所谓的差异项来建模的，该差异项也被分配了 gp 先验。引入差异项是避免由于计算机模型的错误指定而导致参数估计有偏差的关键（Brynjarsd´ottir 和 O’Hagan，2014 年）。 $koh$ 模型以贝叶斯方式处理，使其适用于不确定性量化是重要要求的问题。当人们有兴趣对感兴趣的参数得出结论、对具有与预测相关的特定成本的决策进行预测，或者对迭代改进实验设计感兴趣时，通常会出现这种情况。

虽然 koh 模型和推理为解决昂贵计算机模型校准的不确定性量化提供了一个有吸引力且优雅的框架，但我们的目标是通过这项工作克服一些限制。从建模的角度来看，gps 确实是灵活的仿真器，只要选择了合适的协方差函数，就像在非平稳 gps 的文献中一样（例如 Paciorek 和 Schervish 2003）。然而，最近的方法，如 Deep gps (dgps; Damianou and Lawrence 2013) 已经显示出对许多类函数的极大建模灵活性，并且与 gps 相比，可能会导致计算机模型和真实过程的仿真更加准确。从计算的角度来看，gps 较差的可扩展性继承了局限性（Rasmussen 和 Williams，2006 年），当代码运行次数和实际观察次数加起来超过几千次时，推理变得不切实际。此外，如果没有仔细调整和巧妙的参数化，使用马尔可夫链蒙特卡罗 (mcmc) (Neal, 1993) 技术对 gp 模型进行推理可能会非常缓慢（Filippone et al., 2013; Filippone and Girolami, 2014） .

这项工作旨在通过建议使用 $gp$ 和 $dgp$ 文献中的最新发展以及变分推理来解决这些问题:
(i) 使用 $dgps$ 扩展 $gps$ 在仿真中的建模能力；
(ii) 扩展 Kennedy 和 O’Hagan (2001) 中的原始框架，将模型转换为 $dgp$ 的特例；
(iii) 在 Cutajar 等人的工作的基础上调整基于随机特征扩展和随机变分推理的技术。 （2017），为计算机模型的贝叶斯校准获得一个可扩展的框架。由于这个公式，可以获得一种灵活的校准方法，该方法很容易在具有自动微分和利用 GPU 类型硬件的开发环境中实现。

我们在各种校准问题上验证了我们的提议，我们将其命名为 $DGP-CAL$，并与最先进的替代方案进行了比较。我们展示了 $dgp-cal$ 的灵活性和可扩展性，以及捕捉模型参数和模型差异的不确定性的能力。我们通过展示我们如何进行自适应实验设计以及讨论所提出的校准模型的可识别性来结束本文。复制论文中所有结果的代码可在以下 url 获得：

https://github.com/SebastienMarmin/variational-calibration

2.背景

在本节中，我们介绍了计算机模型的校准问题，并介绍了 $koh$ 模型。 然后我们介绍高斯过程 ($gps$)，它是 $koh$ 模型中的主要建模成分。 受与使用 $gps$ 进行推理相关的困难的启发，我们提出了随机特征扩展作为降低复杂性并能够利用近似推理的最新进展的一种方式。 特别是，我们专注于能够对小批量数据进行操作并且可以在具有自动微分功能的开发环境中轻松实现的变分推理 $(vi)$ 技术。 我们通过展示我们如何通过组合过程来增加 $gps$ 的灵活性来结束本节，获得 $dgps$，为此我们可以扩展随机特征扩展和 $vi$ 的使用。 该背景材料为我们提供了在第 3 节中展示我们提出的校准模型的所有要素。

2.1 贝叶斯校准

考虑对由计算机模型近似的现象进行预测和不确定性量化，这评估起来很昂贵。 在整篇论文中，我们将假设计算机模型的输出是单变量的，但我们将讨论处理多重响应的方法。 我们用 $y\in R$ 表示来自感兴趣的真实现象的观察结果，并且我们假设我们有 $n$ 个可用的 $y=[y_1,...,y_n{]}^T$用于多个输入 $X=[x_1,...,x_n{]}^T$ , 其中$x_i\in D_1\subset R^{d1}$,比如，在气候模型中，$y$ 可以对应于由纬度和经度标识的 $n$ 个位置的温度测量值（在这种情况下$D_1=[-90,90]\times [-180,180]$）。模拟真实现象的计算机模型需要所谓的校准参数 $\theta \in D_2\subset R^{d_2}$ 以及输入变量 $x\in D_1$。校准参数可能具有物理意义（例如，确定碳循环的汇率），对这些参数的推断是贝叶斯校准的核心目标。

除了与 $X$ 相关的观测值 $y$ 之外，计算机模型在（可能不同的）输入 $X^{\ast }=[x_1^{\ast },...,x_N^{\ast }{]}^T$和校准参数 $T=[t_1,...,t_N{]}^T$ 下运行 ，产生一组输出 $z=[z_1,...,z_N{]}^T$。请注意，我们用 $T$ 表示运行计算机模型的 $N$ 个参数配置的集合，而 $\theta$ 表示我们有兴趣推断的真实（未知）参数。 通常 $N$ 大于 $n$，因为与获得真实世界的观察结果相比，运行计算机模型更容易（尽管计算成本很高）。

根据 Kennedy 和 O’Hagan (2001) 中对 koh 模型的定义，我们假设 $y$（观测值） 和 $z$ （计算机输出）是从 $p(y_i|f_i)$ 和 $p(z_j|{\eta }_j^{\ast })$ 中得出的，这决定了似然函数。 向量 $f=[f_1,...,f_n{]}^T$和 ${\eta }^{\ast }=[{\eta }_1^{\ast },...,{\eta }_N^{\ast }{]}^T$是映射 $(x_i,\theta {)}_{i=1,...,n}$ 和 $(x_j^{\ast },t_j{)}_{j=1,...,N}$ 分别通过随机函数 $f$ 和 $\eta$ 得到的。 具有潜在表示 $\eta$ 的计算机模型与具有潜在表示 $f$ 的真实现象之间的联系由下式建模

$$f(x,t)=\eta (x,t)+\delta (x)\text{\hspace{1em}(2.1)}$$
其中 $\delta (x)$ 表示计算机模型与实际过程之间的差异。
图 1 说明了 koh 校准模型。

在他们的贝叶斯公式中，Kennedy 和 O’Hagan (2001) 假设 $\eta (x,t)$ 和 $\delta (x)$ 是独立的高斯过程 (gps)； 换句话说，koh 模型假设这些函数有一个给定的先验分布，它采用 $gp$ 的形式。 此外，他们假设了 θ 的先验，并且他们的目标是根据对真实过程的观察和计算机模型的运行来表征 $\theta$ 的后验分布。 为了保持符号简洁，我们用 $\psi$ 表示 $\eta (x,t)$ 和 $\delta (x)$ 的 $gp$ 参数集，我们用 $U$ 表示所有输入位置 $X$、$X^{\ast }$、$T$的集合。 $koh$ 模型的边际似然是:

$$p(y,z|U,\psi )=\int p(y|{\eta }_{\theta }+\delta )p(z|{\eta }^{\ast })p(\delta |X,\psi )p({\eta }_{\theta },{\eta }^{\ast }|\theta ,U,\psi )p(\theta )d{\eta }^{\ast }d{\eta }_{\theta }d\theta$$

向量 ${\eta }^{\ast }=[\eta (x_1^{\ast },t_1),...,\eta (x_N^{\ast },t_N){]}^T$，${\eta }_{\theta }=[\eta (x_1^{\ast },\theta ),...,\eta (x_N^{\ast },\theta ){]}^T$，$\delta =[\delta (x_1),...,\delta (x_n){]}^T$，
该被积函数相对于感兴趣的参数 $\theta$ 的高维性和非平凡相关性使得它们的推断难以处理，因此需要近似值。 可以对预测分布进行类似的考虑，即 $koh$ 模型在新输入值下所做的考虑。 在 Kennedy 和 O’Hagan (2001) 的原始工作中，使用 $mcmc$ 进行推理，它提供了收敛到模型参数的真实后验分布的保证，但是现场观察的数量和计算机模拟的规模很大。 这是由于 $gps$ 的可扩展性较差，这增加了在 $mcmc$ 内重复解决这些问题的需要。

值得一提的是与 koh 模型相关的可识别性问题，在 Kennedy 和 O’Hagan (2001) 的论文的讨论中提出。这些问题是由于模型的过度参数化而出现的，从而可能混淆校准参数和模型差异的影响。特别是，koh 校准模型在 $\theta$ 和 $\delta (x)$ 上产生联合后验分布，但随着观察次数的增加，koh 模型将此后验集中在流形上，

M = { ( t , δ ( x ) ) ∣ η ( x , t ) + δ ( x ) = f ( x , t ) w i t h x ∈ X ∪ X ∗ } M=\{ (t,δ(x))|η(x,t)+δ(x)=f(x,t) with x∈X∪X^* \} M={(t,δ(x))∣η(x,t)+δ(x)=f(x,t)withx∈X∪X∗}

Brynjarsd´ottir 和 O’Hagan (2014) 很好地说明了这一点问题，因为他们研究如何消除差异将导致模型参数 $\theta$ 的估计有偏差的模型。论据是，如果 $\eta (x,\theta )$ 不能准确地模拟真实的物理过程并且没有差异，那么 $\theta$ 的估计将基于错误指定的模型。增加观察次数并不能解决模型指定错误的基本问题。结论是 koh 模型中的差异对于希望对计算机模型的校准参数 $\theta$ 进行合理推断是必要的，并且对 $\theta$ 和 $\delta (x)$ 施加良好的先验对于减轻缺乏可识别性变得至关重要。或者，当有多个响应可用时，可以提高可识别性，并且这些响应相互依赖于同一组校准参数 θ (Arendt et al., 2012)。在文献中，有一些工作使用替代公式解决 koh 模型的可识别性问题，例如损失最小化 (Tuo and Wu, 2016) 或频率论公式 (Wong et al., 2017)。在这一系列工作中，假设最优 θ 是损失函数的优化器，Plumlee (2017) 表明，$\delta (x)$ 的先验应该与计算机模型的梯度正交。我们注意到可识别性问题以类似的方式影响我们在这里提出的模型，并且我们将部分讨论用于评论我们如何采用文献中的当前策略来处理这个问题。

2.2 高斯过程和随机特征展开

高斯过程 (gp) 是一组随机变量，使得这些随机变量的任何子集都以高斯形式联合分布 (Rasmussen and Williams, 2006)该定义使它们适合分配先验函数。对函数 $g_{exact}(u),u\in D\subset R^d$ 施加 gp 先验意味着对函数 $[g_{exact}(u_1),...,g_{exact}(u_l),]$,在一个集合 $l$ 个输入 $u_1,...,u_l$, 实现分配先验。使得这是多元高斯; 这是因为多元高斯分布的边际特性。需要指定的是均值函数和协方差函数 $c(u_i,u_j)$，它决定了函数在不同输入处的实现如何协变，因此可以从 gp 中得出函数的属性。为简单起见，我们假设一个恒定的零均值，但添加参数均值函数很简单。当 $l$ 超过几千时，涉及 gps 的模型的推理很快变得难以处理。原因是从 gps 和后验推断中采样需要对通过评估所有可能输入对之间的协方差函数获得的协方差矩阵进行代数运算。这些操作通常涉及 $O(l^3)$ 操作，并且需要为协方差矩阵存储 $O(l^2)$个项。在这项工作中，我们通过建立一个模型近似来绕过这些限制，从而将复杂性降低到 $O(l)$，正如我们稍后讨论的那样。

请注意，在 gps 的简短介绍中，我们假设函数是单变量的，即 $g_{exact}(u)\in R$。将其扩展到多变量函数 $g_{exact}(u)\in R^o$ 相当简单。 需要指定的是更丰富的协方差结构，才能够刻画$(g_{exact}{)}_r(u_i)$和$(g_{exact}{)}_r(u_j)$之间的协方差； 例如，参见 A’lvarez 和 Lawrence (2011) 对这些场景的广泛处理。 当我们假设函数之间的协方差为零时，我们有效地将每个 $g_r(u)$ 建模为一个独立的 gp。 我们可以自由地单独参数化每个 gp，或者使用公共协方差 $c(u_i,u_j)$，以便在 $o$ 个函数之间共享协方差参数。 在本文中，我们更喜欢后一种方法以避免引入过多的参数，尽管我们可以很容易地在我们的实现中加入更高级的建模假设。

对于一大类协方差函数，可以证明从 gp 先验得出的结果是可能无限数量的基函数与高斯分布权重的线性组合（Neal，1996；Rasmussen 和 Williams，2006）。 这可以将 $u\in D$ 表述为一个无限和:

$$g_{exact}(u)={\varphi }_{\infty }(u{)}^T{w}_{\infty }\text{\hspace{1em}(2.2)}$$

$w_{\infty }$ 是无限维随机向量，具有 i.i.d. 标准正态分量和 ${\varphi }_{\infty }$ 在 $u$ 处对无限组基函数的评估。 $g_{exact}$ 的精确协方差很容易获得为 $\forall u,u^{\prime }\in D$

$$c(u,u^{\prime })=E[{\varphi }_{\infty }(u{)}^T{w}_{\infty }{w}_{\infty }^T{\varphi }_{\infty }(u^{\prime })={\varphi }_{\infty }(u{)}^T{\varphi }_{\infty }(u^{\prime })]\text{\hspace{1em}(2.3)}$$

由协方差函数引入的无限的表示方式提出了一种通过 ${\varphi }_{\infty }(u)$ 的有限维截断来近似 gps 的方法，我们将其表示为 $\varphi (u)\in R^p$，因此

$$c(u,u^{\prime })={\varphi }_{\infty }(u{)}^T{\varphi }_{\infty }(u^{\prime })\approx \varphi (u{)}^T\varphi (u^{\prime })\text{\hspace{1em}(2.4)}$$
然后函数 $g_{exact}(u)$ 近似为

$$g_{exact}(u)\approx g(u)=\varphi (u{)}^{T}w\text{\hspace{1em}(2.4)}$$

当使用 gps 对具有 $l$ 个观测值的问题进行建模时，截断具有避免使用协方差矩阵求解昂贵的代数运算的优点。 相反，截断将 gps 转换为广义线性模型。 为了保留 gps 的概率特性，很自然地以贝叶斯方式处理这些模型，这需要对大小为 $p\times p(costO(p^3))$ 的矩阵进行代数运算，而相对于 $l$ 的复杂度是线性的 .

随机特征扩展（Rahimi 和 Recht，2008 年；La´zaro-Gredilla 等人，2010 年）提供了一个优雅的框架来构建有限的 p 维表示 $\varphi (u)$，称为随机特征。 作为一个工作示例，在本文中，我们考虑了高斯协方差（或核）函数，也称为平方指数或径向基协方差函数：

$$c(u,u^{\prime })={\sigma }^{2}exp(-\frac{1}{2}(u-u^{\prime }{)}^T{A}^{-1}(u-u^{\prime }))\text{\hspace{1em}(2.6)}$$
对称正定矩阵 A 控制输入的缩放和混合，而 ${\sigma }^2$ 控制 $gp$ 的边际方差。 当协方差是移位不变的时，可以将协方差表示为正测度的傅里叶变换（Rahimi 和 Recht，2008）。 将傅里叶变换应用于高斯协方差，并定义 $\iota =\sqrt{-1}$，我们得到：

$$c(u_i,u_j)={\sigma }^2\int p(\omega )exp(\iota (u_i-u_j{)}^T\omega )d\omega \text{\hspace{1em}(2.7)}$$

这立即表明分布 $p(\omega )$ 也是高斯分布，其形式为 $p(\omega )=N(0,A)$。 通过从 p(ω) 采样，我们可以通过 Monte Carlo 逼近傅里叶公式中的积分，从而获得协方差的有限维表示：

$$c(u_i,u_j)\approx \frac{2{\sigma }^2}{N_{RF}}\sum _{i=1}^{N_{RF}/2}exp(\iota (u_i{)}^T{\hat{\omega }}_r)exp(-\iota (u_j{)}^T{\hat{\omega }}_r)\text{\hspace{1em}(2.8)}$$

在这个表达式中，我们对 ω 中$N_{RF}/2$ 个值进行采样，用 ${\hat{\omega }}_r$ 表示，并利用移位不变性的特性将复指数分成两部分。 虽然基函数很复杂，但通过认识到左侧是实数，对右侧进行简单的三角运算，可以将前面的方程表示为等价形式

$$c(u_i,u_j)\approx \frac{2{\sigma }^2}{N_{RF}}\sum _{i=1}^{N_{RF}/2}[sin(u_i^T{\hat{\omega }}_r),cos(u_i^T{\hat{\omega }}_r)][sin(u_j^T{\hat{\omega }}_r),cos(u_j^T{\hat{\omega }}_r){]}^T\text{\hspace{1em}(2.9)}$$

因此，引入 $\varphi$ : $R^{N_{RF}}$ → $R^{N_{RF}}$ 作为正弦（对于第一个 $N_{RF}/2$ 分量）和余弦（对于最后 $N_{RF}/2$ 分量）的元素应用，得到的基函数是
$$\varphi (u)=\sqrt{\frac{2{\sigma }^2}{N_{RF}}}[sin(u^T\Omega ),cos(u^T\Omega ){]}^T\text{\hspace{1em}(2.10)}$$

其中$\Omega =[{\omega }_1,...,{\omega }_{N_{RF/2}}]$ sin 和 cos 函数按元素应用于它们的参数。 基函数也称为随机特征，因为它们是通过将输入 $u_i$ 与随机矩阵 $\Omega$ 相乘，然后应用非线性来获得的。 例如，可以对 Mat´ern 协方差进行类似的考虑，其中 $\omega$ 是根据多元 Student-t 分布进行采样的。 另请参见 Cho 和 Saul (2009) 的另一种推导，该推导显示如何通过从 $p(\omega )=(0,A)$ 采样 ω 并使用校正线性单元以类似的方式近似一阶的反余弦协方差 非线性 (如果 x > 0, h(x) = x 否则h(x) = 0 ），这在深度神经网络的文献中非常流行。

2.3 深度高斯过程和随机特征扩展

深度高斯过程 (dgp) 定义为函数的组合：
$$g_{deep}(u)=g^{(L)}(g^{(L-1)}(...(g^{(1)}(u))...))\text{\hspace{1em}(2.11)}$$

其中每个函数 $g^{(i)}(\cdot )$ 都被分配了一个 gp 先验（Damianou 和 Lawrence，2013；Neal，1996）。 同样，为简单起见，我们将重点放在单变量 gps 上，但我们将很快讨论处理多变量 gps 的方法。 该组合可以被解释为将 $g^{(i)}$ 的输出作为输入提供给另一个 $g^{(i+1)}$ 的一种方式。 与深度神经网络相比，每个 gp 都可以被认为是一个“层”。 合成操作使 $dgp$先验与 $gps$ 大不相同； 也就是说，$g^{(L)}(u)$ 在 $U$ 处的实现通常不再是多元高斯分布。 我们建议读者参考 Neal (1996)； 杜维诺等人。 （2014）； 马修斯等人。 （2018）对gps的组成进行了一些深入的讨论和说明。

由组合中的函数选择 $gp$ 先验所诱导的 $dgp$ 先验可以用作统计模型中的函数的先验。 在选择合适的似然函数后，人们通常对优化所有模型参数感兴趣，其中包括 $gps$ 在所有层的协方差参数，在 $U$ 处表征 $g^{(L)}(u)$ 的后验，并预测任何 $u^{\ast }$。 对于 dgps，由于组合引入的非平凡依赖性，这些任务在分析上是难以处理的。 大多数关于 dgps 的文献都扩展了为“浅层”gps 开发的近似和推理技术。 例如，亨斯曼和劳伦斯 (2014)； Salimbeni 和 Deisenroth (2017) 将 Nytr¨om 型近似（也称为诱导点近似）的使用扩展到 dgps 并使用变分技术进行推理，而 Bui 等（2016）采用期望传播。

这项工作的重点是 dgps 的随机特征扩展，这是在 Gal 和 Ghahramani (2016) 中提出和研究的； 卡塔哈尔等人。 （2017）。 在这个框架中，组合中的每个 gp 都是通过随机特征来近似的，如上一节所示。 通过这种近似，每个 gp 层都变成了一个线性模型，在权重上具有给定的分布。 用 a 表示第 (i) 层的输入，第 i 层的 gp 用随机特征近似实现以下操作：
$${\varphi }^{(i)}(a)=\sqrt{\frac{2({\sigma }^2{)}^{(i)}}{N_{RF}^{(i)}}}[sin({\Omega }^{(i)}a{)}^T,cos({\Omega }^{(i)}a{)}^T{]}^T,g^{(i)}(a)=({\varphi }^{(i)}{)}^T{w}^{(i)}\text{\hspace{1em}(2.12)}$$

通过这种近似，每个 gp 层都可以看作是一个两层神经网络。第一层通过随机矩阵 ${\Omega }^{(i)}$ 实现乘法，并通过三角函数应用非线性。第二层实现输入的线性组合。因此，组合这些近似 $gps$ 会产生一种特定形式的贝叶斯深度神经网络。在传统的深度神经网络中，每一层都应用了非线性，并且所有的权重都得到了优化；在被视为贝叶斯深度神经网络的近似 $dgp$ 中，每隔一层应用非线性，并且仅推断 $w^{(i)}$ 权重，而 ${\Omega }^{(i)}$ 是随机的。见 Cutajar 等人。 (2017) 深入讨论了与贝叶斯深度神经网络的联系以及可以处理 ${\Omega }^{(i)}$以提高性能的其他方式。

具有随机特征的模型近似绕过了必须处理 $gps$ 组成的推理的挑战，但是由于基函数引入的非线性，从贝叶斯的角度来看，生成的线性模型的组成仍然是棘手的。在下一节中，我们将介绍变分推理，作为一种为用随机特征近似的 $dgps$ 推导出易于处理和可扩展的推理方案的方法。

2.4 随机变分推理

暂略

3 用于校准计算机模型的 DGP

在本节中，我们将介绍我们的贡献，我们将其称为 dgp-cal。 我们首先观察到 koh 校准模型可以被视为 dgp 的一个特例，这使我们能够将 koh 模型的原始公式推广到更灵活的公式。 然后，我们展示了如何利用前几节中介绍的 dgps 近似和推理方面的进步，即随机特征扩展和随机变分推理，以获得可扩展的校准框架，同时保持使用 dgps 提供的灵活性 . 我们通过讨论实现细节来结束本节。

3.1 将 KOH 校准模型推广为 DGP

koh 校准模型的原始公式涉及使用 gps 来模拟计算机模型并模拟加性差异。 正如 Kennedy 和 O’Hagan (2001) 所指出的，加性差异有些特殊，并且可以推广（参见例如，Qian 和 Wu 2008）。 我们建议通过假设真实过程的底层函数是通过应用于仿真器的扭曲函数 $\gamma$ 获得的：
$$f(x,t)=\gamma (\eta (x,t),x)\text{\hspace{1em}(3.1)}$$

当翘曲将恒等式应用于 $\eta (x,t)$ 并将其添加到 $x$ 上的 gp 时，我们检索了 koh 公式（2.1）。 换句话说，我们可以把koh模型中的函数$f(x,t)$看作是两个函数的组合； 第一个是一个 gp，给定输入 x 和 t，产生 η(x, t)，而第二个应用 η 和另一个具有固定单位权重的 gp δ(x) 的线性组合。

在 koh 模型的原始公式中，计算机代码与实际过程之间的差异通过加性差异项 $\delta (x)$ 来建模。 相反，在 koh 模型的建议推广中，我们假设 gp 先验在 $\gamma (\eta (x,t),x)$ 上，因此我们将扭曲作为 $x$ 的函数。 与原始 koh 模型类似，对翘曲函数 $\gamma (\eta (x,t),x)$的分析允许人们推断计算机模型与实际过程之间的差异。

我们在工作中实现的另一个可能的扩展是通过让 $\eta (x,t)$ 和/或 $\gamma (\eta (x,t),x)$ 被建模为 $dgps$ 而不是 $gps$ 来增加模型的灵活性。 当仿真器或实际过程表现出难以通过设计适当的协方差函数来建模的空间相关行为时，深度扩展特别有用。 $dgps$ 提供了一种从数据中学习此类非平稳性的方法，因此这在此类具有挑战性的应用中特别有吸引力。 我们将举例说明 $dgps$ 和实验中的广义公式。 由于可以在广义模型中使用 dgps 的随机特征近似，我们可以获得一个可扩展的校准框架，如下所述。

3.2 使用随机特征的模型逼近

在本节中，我们将讨论如何使用随机特征近似来使 koh 模型及其泛化适用于变分推理。 我们从 koh 模型开始，假设 $\eta (x,t)$ 和 $\delta (x)$ 用 (2.6) 中的高斯协方差建模为 $gps$； 我们分别用 $A_{\eta }$ 和 $A_{\delta }$ 以及它们的边际方差 ${\sigma }_{\eta }^2$ 和 ${\sigma }_{\delta }^2$ 来表示它们的各向异性矩阵。 通过应用 2.2 节中详述的随机特征扩展，我们得到
$$\eta (x,\theta )={\varphi }_{\eta }(x,\theta {)}^T{w}_{\eta }={\sigma }_{\eta }\varphi {\left({\Omega }_{\eta }\left[\begin{array}{c}x\\ \theta \end{array}\right]\right)}^T{w}_{\eta }\text{\hspace{1em}(3.2)}$$
$$\delta (x)={\varphi }_{\delta }(x{)}^T{w}_{\delta }={\sigma }_{\delta }\varphi ({\Omega }_{\delta }x{)}^T{w}_{\eta }\text{\hspace{1em}(3.3)}$$
特征图 ${\varphi }_{\eta }$ 和 ${\varphi }_{\delta }$ 使用函数 $\varphi$ : $R^{N_{RF}}\to R^{N_{RF}}$在（2.10）中给出。 大小为 $N_{RF}$ 的 $w_{\eta }$ 和 $w_{\delta }$ 的元素具有 i.i.d. 标准正态先验，而大小为 $N_{RF}\times (d_1+d_2)$、$N_{RF}\times d_1$ 的矩阵 ${\Omega }_{\eta }$、${\Omega }_{\delta }$ 具有 i.i.d行正态，协方差取决于正定矩阵 $A_{\eta }$ 和 $A_{\delta }$； 特别是，${\Omega }_{\eta }$ 和 ${\Omega }_{\delta }$ 的列是 i.i.d。 分别为$N(0,A_{\eta })，N(0,A_{\delta })$。 图 2 表示根据 (2.1)、(3.2) 和 (3.3) 的模型（使用类似神经网络的图）。

通过将随机特征扩展应用于每个 $gp$ 层，可以直接将此公式扩展到使用 $dgps$ 而不是 $gps$ 对 $\eta (x,t)$ 和 $\delta (x)$ 建模。 假设每个 $dgp$ 都有 $L_{\eta }$ 和 $L_{\delta }$ 层，在这种情况下，$\eta (x,t)$ 和 $\delta (x)$ 由贝叶斯深度神经网络近似，其中每个 gp 层近似为：

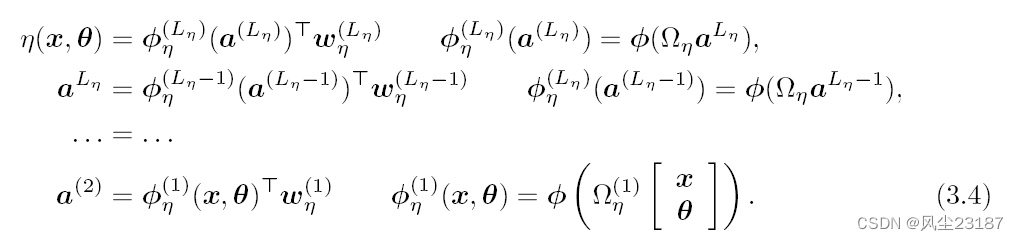
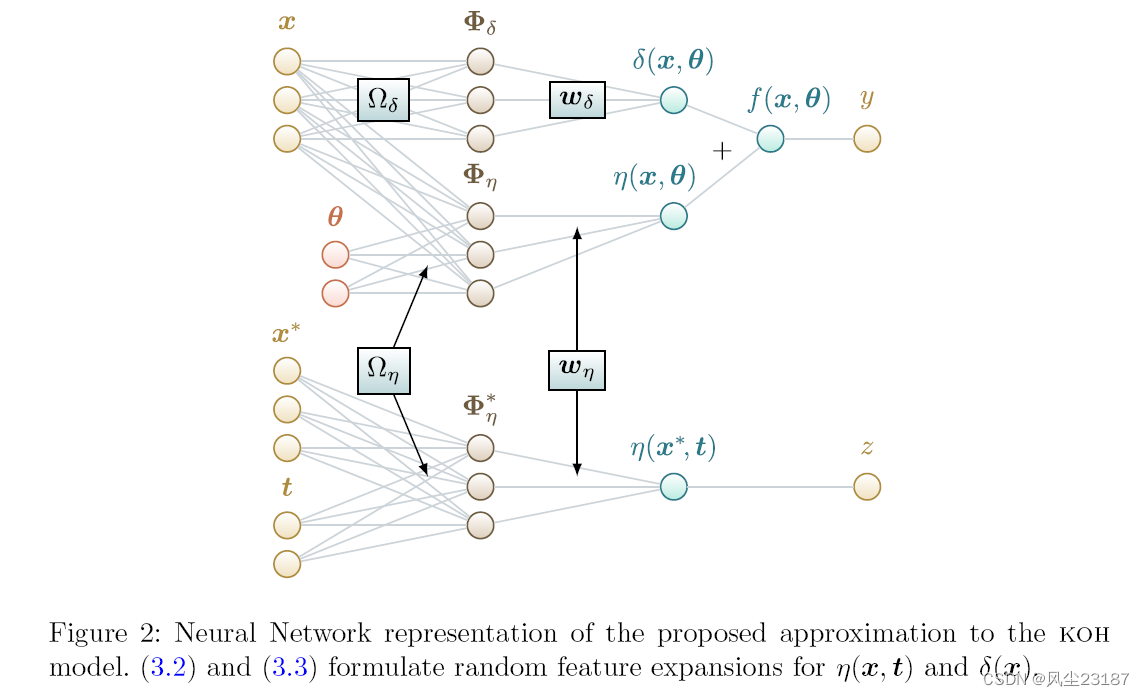
图 2：提出的 koh 模型近似值的神经网络表示。 (3.2) 和 (3.3) 为 η(x, t) 和 δ(x) 制定随机特征扩展。

类似地，我们可以为 koh 模型中的 dgp 建模 $\delta (x)$ 构造一个随机特征近似，或者在 koh 模型的广义版本中对翘曲函数 $\gamma (\eta (x,t),x)$ 应用相同的构造 . 所提出的使用随机特征近似的优点是它可以使用第 3.3 节中介绍的随机变分推理，如下所述。

3.3 近似DGP校准模型的推断

同样，我们专注于使用差异项 $\delta (x)$ 而不是翘曲 $\gamma (\eta (x,t),x)$ 的 $koh$ 模型的框架，但是对于后一种情况很容易遵循相同的推导。 我们利用变分推断 (vi)，因此我们通过引入变分后验 $q(w_{\eta },w_{\delta },\theta )$ 来近似所有模型参数 $w_{\eta }、w_{\delta }$ 和 $\theta$ 的后验分布，参见第 2.4 节。 我们假设 $q(w_{\eta },w_{\delta },\theta )$ 是高斯的并且在参数之间完全分解，即
$$q(w_{\eta },w_{\delta },\theta )=\prod _{i=1}^{N_{RF}}\prod _{j=1}^{d_{out}}q(w_{\eta ,ij})q(w_{\delta ,ij})\prod _{l=1}^{d_2}q({\theta }_l)\text{\hspace{1em}(3.5)}$$
虽然分解假设可以放宽。 假设 $q(w_{\eta },w_{\eta },\theta )$ 跨参数分解，我们处理与模型参数数量呈线性关系的计算和存储。 放宽分解意味着假设某些参数组具有非零协方差。 例如，可以假设 $q(w_{\eta ,\cdot j})=N({\mu }_{\eta ,j},{\Sigma }_{\eta ,j})$ 并参数化 ${\Sigma }_{\eta ,j}=L_{\eta ,j}{L}_{\eta ,j}^T$ 以通过优化 $L_{\eta ,j}$ 来保持正定性。 很容易验证这种选择需要 $O(N_{RF}^2)$ 存储和 $O(N_{RF}^3)$ 计算。

遵循 vi 的原则，我们需要推导出模型边际似然的下界，并在分布 $q(w_{\eta },w_{\delta },\theta )$ 上最大化它。在实践中，这个问题变成了关于控制 $q(w_{\eta },w_{\delta },\theta )$ 的参数的下界优化。取下界 (2.14) 及其无偏蒙特卡罗和基于小批量的近似值 (2.17)，我们现在将其调整为我们的校准模型。在这个适应中，我们意识到有两种类型的输入点，即观测 X 和计算机运行 $[X^{\ast },T]$；请注意，$X、X^{\ast }$ 和 $T$ 的形状不允许将这三个矩阵串联在一个矩阵中。一种可能性是对数据集的联合应用小批量。但是，如果不确保每个类别（“观察”与“运行”）得到充分代表，我们不推荐此过程。例如，对 n << N 的输入点的类别视而不见的均匀抽样会使抽样观测的数量在一次迭代之间变化很大，有时可能不会对它们进行抽样。一种解决方法是绘制两个索引集 I ⊂ { 1 , . . . , n } I ⊂ \{1, . . . , n\} I⊂{1,...,n} 和 J ⊂ { 1 , . . . , N } J ⊂ \{1, . . . , N\} J⊂{1,...,N} 的大小为 m 和 M。下界的拟合项现在可以近似为

$({\tilde{w}}_{\eta }{)}_{(k)},({\tilde{w}}_{\delta }{)}_{(k)},{\tilde{\theta }}_{(k)}$ i.i.d. 来自 $q(w_{\eta },w_{\delta },\theta )$ 的样本。 当先验和后验都是高斯时，可以使用（2.15）轻松计算正则化项。

3.4 实施细节

考虑到要优化的参数数量较多，将优化过程分为几个阶段。 我们首先关注计算机模型响应； 除了影响 $z$ 预测的参数，即 $\sigma z$之外。$w_{\eta }$ 的分量的均值和方差以及 $\eta (x,t)$ 的 gp/dgp 参数之外，所有参数都是固定的。 在第二阶段释放所有其他参数以联合推断 $y$ 和 $\theta$，即添加 $\delta (x)$ 或 $\gamma (\eta (x,t),x)$ 的权重和超参数。 在每个阶段，我们首先优化 $\theta$ 的均值和方差，然后以较小的学习率联合所有参数。

为了初始化 dgp（或 gp）$\eta (x,t)$ 的权重，我们使用 Rossi 等人提出的方法。 （2019），这是一种基于贝叶斯线性回归的可扩展的分层初始化策略。这个想法是执行一系列回归任务，将每一层映射到标签，以便可以获得变分分布的合理初始参数。从第一层开始，我们从输入 $X^{\ast }$ 和 $T$ 到标签 $z$ 执行贝叶斯线性回归，以便我们可以估计第一层参数的后验。然后我们冻结这个分布并使用给定的输入数据 $X^{\ast }$ 和 $T$ 计算第一层的输出。然后将该结果用作第二层的输入，通过对标签执行回归来估计相应的线性模型 $z$。然后我们迭代地进行到最后一层。直观地说，这种初始化促进了第一层已经能够获得合理回归结果的配置，而更接近标签的层则用作细化。

我们定义了例程 $\mu ,\Sigma \leftarrow LM(X_{LM},y_{LM})$，它对一组输入-输出对 $X_{LM}$, $y_{LM}$ 执行贝叶斯线性回归。该例程返回工具回归 $y_{LM}:=z=X_{LM}w+{\sigma }_{\eta }^2\epsilon$中权重 $w$ 的后验分布的均值和协方差，其中 ${\sigma }_{\eta }^2$ 是似然函数的方差，以及 $w$ 的分量的先验， $\epsilon$ 是 i.i.d的$N(0,1)$。通过这些定义，算法 1 中报告了初始化。贝叶斯线性回归中的后验分布通常具有完全协方差，而假设的后验分布是完全分解的。在这种情况下，我们使用 Kullback-Leibler 散度将最优分解高斯分布与实际后验分布相匹配，这解释了算法 1 的最后一行中对 $q(W_{\eta ,:,i}^{(l)})$ 的分配。该过程可以正如算法 1 中所报告的，它可以轻松利用 mini-batching，并且可以使用随机优化进行操作，从而使其适用于大规模问题。我们将读者推荐给 Rossi 等人。 (2019) 了解更多详情。

4.实验

在本节中，我们验证了 dgp-cal 在一些校准问题上的作用。 在每个实验中，我们指定 dgp-cal 是使用 (2.1) 中的加法结构，如 $koh$ 公式，还是 (3.1) 中的通用结构； 我们还指定何时使用 dgps 而不是 gps（默认）测试模型。 实验具有以下设置。 可能性 $p(y_i|f_i)$ 和 $p(z_j|{\eta }_j^{\ast })$ 是高斯的，方差 ${\sigma }_y^2$ 和 ${\sigma }_z^2$ 被视为 $\psi$ 内的超参数。 $\eta (x,t)$ 和 $\delta (x)$ 的所有协方差函数都是高斯函数，除了第 4.2 节中使用 Mat´ern 核的比较实验。 变分后验 $q(W_{\eta })q(W_{\delta })q(\theta )$ 和先验 $p(\theta )$ 是高斯分布的。

计算方法

大量文献致力于数值挑战性应用的实用性。 格拉姆西等人 (2015) 使用局部近似 gp 建模并通过求解似然项的无导数最大化来校准参数。 Pratola 和 Higdon (2016) 使用贝叶斯树和回归处理大型问题

输入：

• dgp $\eta =g^{(L)}(g^{(L-1)}(...(g^{(1)}(x,t))))$ 权重的变化分布 w η = { W η ( 1 ) , . . . , W η ( L ) } w_η = \{W^{(1)}_η , . . . , W^{(L)}_η \} wη​={Wη(1)​,...,Wη(L)​} 设置为先验 $N(0,1)$ i.i.d. 于所有组件。
• 计算机运行 $X^{\ast },T$，输出 $z$ 以大小为 M 的小批量组成。
  结果：使用如下算法，开始最大化下限的分布 $q(w_{\eta })$。
  
  用于对来自计算机模型和实际过程的数据进行建模。 最近在 Gu and Wang (2018) 和 Gu (2018) 中，通过直接在差异的 L2 范数上定义先验分布，在贝叶斯框架内执行校准。 Xie and Xu (2018) 通过最小化差异样本路径的 L2 范数，从校准参数的后验分布中采样（类似于 Wong et al. 2017）。 这些作者在 R 或 C++ 包中提供了易于使用的代码。 我们将这些方法分别称为 LaGP、Sum-of-trees、Robust 和 Projected.

4.1 示例

我们在一个带有一个变量和一个校准输入的校准问题上说明了 dgp-cal。作为第一个测试，假设用于生成数据集的先验参数和超参数是已知的，其中 $\theta \sim N(0,1)$, ${\sigma }_{\eta }=1$, $A_{\eta }=\frac{1}{2}I$, ${\sigma }_{\delta }=\frac{2}{10}$, $A_{\delta }=\frac{1}{20}$ .我们以 $[0,1]\times [-5/2,5/2]$ 中的空间填充方式为 $N=7$ 次计算机运行和 $n=4$ 个观察值从真实过程中选择位置。 $(x_i^{\ast }{)}_{i=1,...,N}$ 处的计算机模型的输出向量 $z$ 从其先验分布中采样。为了确定真实的观测值 $y$，我们首先对 $p(\theta )$ 进行采样以获得 ${\theta }_{true}$，然后是 $\delta (x)$ 的采样路径。 $\eta (x,t)$ 和 $\delta (x)$ 的 gp 先验通过 (3.2) 和 (3.3) 用 $N_{RF}=50$ 个随机特征进行近似，并使用 (2.1) 计算观测值。 dgp-cal 的结果如图 3 所示。在第一和第三面板中，我们看到通过积分 $w_{\eta }$ 和 $w_{\delta }$ 分析得到的 $\theta$ 的后验质量集中在真实值$\approx 0.8$ 附近，其中有（颜色）$z$（点）和 $y$（线）之间的匹配。变分后验（蓝线）提供了真实后验的合理近似。

图 3：

• 左上角:θ 的先验（黑色）、分析后验（绿色）和变分后验（蓝色）分布以及用于生成 y（红色）的实际值。
• 右上角：用于生成本例数据集的真实响应 η 和计算机运行的位置（点）。
• 左下：将 y 显示为 D1×D2 中的水平线。 线条的颜色对应于值 $y_i$。 点代表计算机运行 $z$。 灰度级表示 $\theta$ 的后验分布（也显示在左上角的面板中）。
• 右下：$\eta$ 的后验平均值。

4.2 细胞生物学中的模型校准

4.3 复杂响应的模型校准

我们现在处理一个关于计算机模型的局部非平滑/非平稳响应的案例研究，对于这种情况，静态 gp 通常是不够的。该计算机模型是一个模拟地下核试验对放射性核素扩散到美国尤卡平原含水层中的影响（Fenelon，2005 年）。我们采用与 Pratola 和 Higdon (2016) 补充材料中的脚本生成的数据集相同的数据集，该材料可在线获得，$d_1=2,d_2=6,n=10和N=17600$。

在 Pratola 和 Higdon ( 2016），数据集的大小以及非平稳建模通过树和回归进行处理。我们使用带有两层 dgp 仿真器的 dgp-cal 对计算机模型进行校准，以展示更复杂的仿真器捕获表征该问题的非平稳性的能力。因此，我们将 dgp-cal 与浅 gp 仿真器进行比较。有关初始化的详细信息，请参见表 2。此外，我们将模块化方法与 Gramacy 等人的 Local Approximate gps (lagp) 进行了比较。 （2015 年）。

在图 7 中，我们显示了函数 $f(\cdot ,\theta )$ 的后验，对真实观察进行建模。我们观察到，只有深度变分校准和树总和方法才能通过捕获表征一次观察的尖峰来重现数据集的非平稳性质。

图 5：${\eta }_{cell}(\cdot ,\theta )$ 的样本，$\theta$ 取自其后验。 灰点代表计算机运行，白点代表真实观察。

4.4 数据集规模可扩展性

5 讨论

Kennedy 和 O’Hagan (2001) 中的 koh 模型和推理提供了一个经典框架来解决不确定性量化是主要兴趣的校准问题。在本文中，我们提出了 dgp-cal，它比 koh 校准提供了许多改进。从建模的角度来看，我们将 koh 校准模型视为更一般的 dgp 模型的特例，其中模拟真实观察的潜在过程是计算机模型模拟器的扭曲版本；我们表明，这种通用校准模型保留了推理计算机模型与实际过程之间差异的不确定性的可能性。

此外，提出的具有随机特征的 gps 和 dgps 近似以及通过变分技术进行的近似推理为 dgp-cal 带来了许多优势，例如在具有自动微分功能的开发环境中实现的简单性以及利用 GPU 类型硬件的可能性。实验表明，为恢复易处理性而引入的近似值不影响 dgp-cal 有效校准复杂计算机模型参数的能力，同时享有对大量观察和/或计算机运行的可扩展性，这表明 dgp- cal 是最先进的强大替代方案。我们目前正在研究将 dgp-cal 应用于环境科学中的其他大规模校准问题，由于可扩展性有限，koh 模型和相关校准方法通常不是首选。

我们通过讨论这项工作的两个重要方面来结束本文，即自适应实验设计和可识别性。

6. 代码分析

0.导入库

import os, sys
from os.path import isfile, join
from os import listdir
sys.path.append(os.path.join(os.path.dirname(__file__), ".."))
import subprocess # only for launching the script generating the figures

import argparse
import numpy as np
import torch
torch.set_num_threads(32) 
from torch.utils.data import DataLoader, TensorDataset
from torch.utils.data.dataset import random_split
#from collections import OrderedDict

import timeit
import time
import vcal
from vcal.nets import AdditiveDiscrepancy, RegressionNet, GeneralDiscrepancy
from vcal.layers import FourierFeaturesGaussianProcess as GP
from vcal.stats import GaussianVector
from vcal.utilities import MultiSpaceBatchLoader,SingleSpaceBatchLoader, gentxt, VcalException
from vcal.vardl_utils.initializers import IBLMInitializer

import json

import matplotlib
from matplotlib import pyplot as plt
import timeit

1. 参数获取

• –dataset：数据集
• –dataset_dir：数据集路径
• –split_ratio_run：计算机运行的训练/测试拆分比率
• –split_ratio_obs：真实观察的训练/测试分割比
• –verbose：训练步骤的详细程度
• 训练期间的蒙特卡洛样本数
• 测试期间的蒙特卡洛样本数
• 实际观察训练期间的批量大小
• 计算机运行训练期间的批量大小
• 等等

def parse_args():
    #available_models = models.keys()
    available_datasets = ["calib_borehole","calib_currin","calib_case1","calib_case2","calib_nevada","calib_test_full"]

    parser = argparse.ArgumentParser()
    parser.add_argument('--dataset', choices=available_datasets, type=str, required=True,
                        help='Dataset name')
    parser.add_argument('--dataset_dir', type=str, default='/mnt/workspace/Datasets',
                        help='Dataset directory')
    parser.add_argument('--split_ratio_run', type=float, default=1,
                        help='Train/test split ratio for computer runs')
    parser.add_argument('--split_ratio_obs', type=float, default=1,
                        help='Train/test split ratio for real observations')
    parser.add_argument('--verbose', action='store_true', default=True,
                        help='Verbosity of training steps')
    parser.add_argument('--nmc_train', type=int, default=1,
                        help='Number of Monte Carlo samples during training')
    parser.add_argument('--nmc_test', type=int, default=100,
                        help='Number of Monte Carlo samples during testing')
    parser.add_argument('--batch_size_obs', type=int, default=20,
                        help='Batch size during training for real observations')
    parser.add_argument('--batch_size_run', type=int, default=20,
                        help='Batch size during training for computer runs')
    parser.add_argument('--nlayers_obs', type=int, default=1,
                        help='Number of GP layers for discrepancy')
    parser.add_argument('--nlayers_run', type=int, default=1,
                        help='Number of GP layers for computer model')
    parser.add_argument('--nfeatures_run', type=int, default=20,
                        help='Dimensionality of hidden layers for the computer model',)
    parser.add_argument('--additive', type=int, default=1,
                        help='Use additive or general discrepancy',)
    parser.add_argument('--nfeatures_obs', type=int, default=20,
                        help='Dimensionality of hidden layers for the discrepancy model',)
    parser.add_argument('--lr', type=float, default=1e-4,
                        help='Learning rate for training', )
    parser.add_argument('--lr_calib', type=float, default=1e-1,
                        help='Learning rate for training of the variational calibration', )
    parser.add_argument('--model', type=str,
                        help='Type of Bayesian model')
    parser.add_argument('--outdir', type=str,
                        default='workspace/',
                        help='Output directory base path',)
    parser.add_argument('--seed', type=int, default=0,
                        help='Random seed',)
    parser.add_argument('--noise_std_run', type=float, default=0.01,
                        help='Observation noise standard deviation')
    parser.add_argument('--noise_std_obs', type=float, default=0.01,
                        help='Computer run noise standard deviation')
    parser.add_argument('--discrepancy_level', type=float, default=0.05,
                        help='From 0 to 1, how much the additive discrepancy should explain the signals\' stddev?')
    parser.add_argument('--iterations_fixed_noise', type=int, default=100,
                        help='Training iteration without noise optimization')
    parser.add_argument('--iterations_free_noise', type=int, default=100,
                        help='Training iteration with noise optimization')
    parser.add_argument('--test_interval', type=int, default=100,
                        help='Interval between testing')
    parser.add_argument('--time_budget', type=int, default=720,
                        help='Time budget in minutes')
    parser.add_argument('--cuda', action='store_true',
                        help='Training on gpu or cpu')
    parser.add_argument('--save_model', action='store_true',
                        help='Save resulting model')
    parser.add_argument('--full_cov_W', type=int,default=0,
                        help='Switch from fully factorized to full cov for q(W)')
    parser.add_argument('--rff_optim_run', type=int,default=0,
                        help='Optimize the Fourier features instead of lengthscales for comp. model')
    parser.add_argument('--rff_optim_obs', type=int,default=0,
                        help='Optimize the Fourier features instead of lengthscales for discrepancy')
    parser.add_argument('--init_batchsize', type=int,default=10000,
                        help='Maximum number of data points for the initialization')

    args = parser.parse_args()

    args.dataset_dir = os.path.abspath(args.dataset_dir)+'/'
    args.outdir = os.path.abspath(args.outdir)+'/'

    if args.cuda:
        if torch.cuda.is_available():
            args.device = 'cuda'
        else:
            print("Cuda not available. Using cpu.")
            args.device = 'cpu'
    else:
        args.device = 'cpu'
    return args
args = parse_args()

2. 实验配置

• 1. 模型输出路径
• 2. 日志设置
• 3. 将实验配置保存为 yaml 文件到 logdir

proce = True
    if (args.dataset == "calib_nevada" or args.dataset == "calib_borehole") and args.additive==0:
        proce = False
    if (args.dataset == "calib_case2" or args.dataset == "calib_borehole") and args.nlayers_run==2:
        proce = False
    if not proce:
        print("SKIPPING")
    if proce:
        
        try:
            for i in range(400):
                if i>398:
                    print("Problems making the folder "+outdir)
                try:
                    outdir = vcal.vardl_utils.next_path('%s/%s/%s/' % (args.outdir, args.dataset, "additive_"+str(args.additive)) + 'run-%04d/')
                    os.makedirs(outdir)
                    break
                except FileExistsError:
                    time.sleep(.2)        
        except OSError:  
            print ("Creation of the directory %s failed" % outdir)

        if args.verbose:
                logger = vcal.vardl_utils.setup_logger('vcal', outdir, 'DEBUG')
        else:
                logger = vcal.vardl_utils.setup_logger('vcal#', outdir)
        logger.info('Configuration:')
        for key, value in vars(args).items():
                logger.info('  %s = %s' % (key, value))
        # Save experiment configuration as yaml file in logdir
        with open(outdir + 'experiment_config.json', 'w') as fp:
                json.dump(vars(args), fp, sort_keys=True, indent=4)
        vcal.utilities.set_seed(args.seed)
        train_obs_loader,train_run_loader,test_obs_loader,test_run_loader, input_dim, calib_dim,output_dim,true_calib = setup_dataset()
        train_data_loader = MultiSpaceBatchLoader(train_obs_loader,train_run_loader)
        test_data_loader  = MultiSpaceBatchLoader(test_obs_loader,  test_run_loader)

        output_mean_run = train_run_loader.dataset.tensors[-1].mean(-2)
        output_std_run  = train_run_loader.dataset.tensors[-1].mean(-2)
        scale_factor_run = (output_std_run**2).mean().sqrt().item()
        output_mean_obs = train_obs_loader.dataset.tensors[-1].var(-2).sqrt()
        output_std_obs  = train_obs_loader.dataset.tensors[-1].var(-2).sqrt()
        scale_factor_obs = (output_std_run**2).mean().sqrt().item()

        dobs = train_data_loader.loaders[0].dataset
        drun = train_data_loader.loaders[1].dataset
        logger.info("Training observation points: {:4d}, in dimension {:3d}.".format(len(dobs),dobs.tensors[0].size(-1)))
        logger.info("Training computer runs:      {:4d}, in dimension {:3d}.".format(len(drun),drun.tensors[0].size(-1)+drun.tensors[1].size(-1)))
        logger.info("Calibration dimension: {:3d}".format(drun.tensors[1].size(-1)))
        #接下

3. DGP网络构建

• 网络构建
• 模型框架搭建

class DGP(torch.nn.Sequential):
    def __init__(self, input_dim,output_dim,full_cov_W,nlayers,nfeatures,nmc_train,nmc_test,mean,scale,**kwargs):
        gp_list = list() # type: List(torch.nn.Module)
        nl = nlayers
        for i in range(nlayers):
            # Layer widths given by trapezoidal interpolation
            d_in = int((1-i/nl)*input_dim + i/nl*output_dim)
            d_out = int((1-(i+1)/nl)*input_dim + (i+1)/nl*output_dim)
            gp   = GP(d_in,d_out,nfeatures=nfeatures, nmc_train=nmc_train, nmc_test=nmc_test,full_cov_W=full_cov_W)
            if i<nlayers-1:
                gp._stddevs.requires_grad = False
                # Scale factor useful only for the last layer 
                # (because else it is equivalent to the lengthscale of the next GP)
            gp_list += [gp]
        gp_list[-1].mean = mean # last GP fit the data output mean and variance (equivalent to standardize the data)
        gp_list[-1].stddevs = scale
        super(DGP, self).__init__(*gp_list, **kwargs)
        
    def optimize_weights(self,b=True):
        for gp in self:
            gp.optimize_weights(b)
    def fix_hyperparameters(self,b=True):
        for gp in self:
            gp.fix_hyperparameters(b)
eta = DGP(input_dim,output_dim,
		args.full_cov_W,args.nlayers_run,
		args.nfeatures_run,args.nmc_train,
		args.nmc_test,output_mean_run,output_std_run)
for gp in list(eta):
	gp.optimize_fourier_features(args.rff_optim_run==1)
if args.additive == 1:
	dim_delta = input_dim-calib_dim
	scale_delta = args.discrepancy_level * output_std_obs
	mean_delta = torch.zeros(output_dim)
else:
	dim_delta = 1+ input_dim-calib_dim
	scale_delta = output_std_obs
	mean_delta = output_mean_obs
	logger.info("Discrepancy input dimension: {:3d}".format(dim_delta))
	#接上
delta = DGP(dim_delta, output_dim,args.full_cov_W,
			args.nlayers_obs,args.nfeatures_obs,
			args.nmc_train,args.nmc_test,mean_delta,scale_delta)
for gp in list(delta):
	gp.optimize_fourier_features(args.rff_optim_obs==1)

computer_model = RegressionNet(eta)
discrepancy   = RegressionNet(delta)

computer_model.likelihood.stddevs = args.noise_std_run*scale_factor_run
discrepancy.likelihood.stddevs    = args.noise_std_obs*scale_factor_obs

calib_prior = GaussianVector(calib_dim,constant_mean=.5,parameter=False)
calib_prior.stddevs=np.sqrt(calib_dim) # proportional with the length of the hypercube diagonal
calib_posterior = GaussianVector(calib_dim)
calib_posterior.loc.data = torch.ones_like(calib_posterior.loc)*.5
calib_posterior.stddevs = np.sqrt(calib_dim)
# 真实模型
if args.additive == 1:

	model = AdditiveDiscrepancy(computer_model,discrepancy,calib_prior,calib_posterior,true_calib=true_calib)
else:
	model = GeneralDiscrepancy(computer_model,discrepancy,calib_prior,calib_posterior,true_calib=true_calib)

3.1.计算模型初始化

计算批量大小可以有多大

# Compute how big can be the batch size
npts_run = len(train_data_loader.loaders[1].dataset)
init_batchsize_run = min(args.init_batchsize,npts_run)
init_data_run,_=random_split(train_data_loader.loaders[1].dataset,[init_batchsize_run,npts_run-init_batchsize_run])
dataloader_run_for_init=SingleSpaceBatchLoader(DataLoader(init_data_run,batch_size=init_batchsize_run),cat_inputs=True)
computer_model_initializer=IBLMInitializer(computer_model,dataloader_run_for_init,noise_var =0.1*scale_factor_run)
computer_model_initializer.initialize()

tb_logger = vcal.vardl_utils.logger.TensorboardLogger(path=outdir, model=model, directory=None)

阶段1：关闭模型差异并校准

discrepancy.likelihood.stddevs = 2*scale_factor_obs
delta.optimize_weights(False)
delta.fix_hyperparameters(True)
calib_posterior.optimize(False)
### Start
trainer = vcal.learning.Trainer(model, 'Adam', {'lr': args.lr}, train_data_loader,test_data_loader,args.device, args.seed, tb_logger, debug=args.verbose,lr_calib=args.lr_calib)
trainer.fit(args.iterations_fixed_noise, args.test_interval, 1, time_budget=args.time_budget//2)

阶段2：

• 停用计算机模型学习

eta.fix_hyperparameters(True)
eta.optimize_weights(False)

• 重新激活差异和校准

 ### Reactivate discrepancy and calibration
discrepancy.likelihood.stddevs = args.noise_std_obs*scale_factor_obs
delta.optimize_weights(True)
calib_posterior.optimize(True)

开始训练

• 激活观测噪声优化，
• 低初始变分后验方差，用于改进校准参数均值的搜索

### Activate observation noise optim
model.discrepancy.likelihood.optimize(True)
### Low initial variational posterior variance for improvig the search of calib parameter mean
calib_posterior.stddevs = 0.02*np.sqrt(calib_dim)
### Start
logger.info("Stage 1 finished. Stage 2:")
logger.info(model.string_parameters_to_optimize())
trainer.fit(args.iterations_free_noise, args.test_interval, 1, time_budget=args.time_budget//2)
 ###################

记录训练结束：

logger.info("Training finished.")
logger.info("Start testing.")
test_mnll, test_error = trainer.test()
logger.info("Testing finished.")