几何向量：三维点与直线

     在三维图形问题中，点和直线计算是很常见的，比如，已知三维空间中一条直线和任意非直线上的点，求点到直线的垂线（或垂点），这个问题比较典型，基本上就属于一系列三维空间点与直线关系的代表。

     首先如下图：

     

     学到现在的几何向量，一眼就看得出来，只需要根据向量PC1与向量PV的点积等于0，得到方程组就可以最终计算出P点坐标了。首先我们确定三维空间中P点表示法，使用C1 + n*dir的形式，其中C1为起始点，dir为单位朝向向量，n为模长。那么计算如下：

     

     推算出来计算公式，那么程序中验证一下就好了，代码如下：

     

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class VerticalVertex : MonoBehaviour
{
    public Transform C1;
    public Transform C2;

    public Transform Vertex;

    private Vector3 c2;

    void Start()
    {
        c2 = C2.position;
    }

    void Update()
    {
        C2.position = c2 + new Vector3(0, 0, Mathf.Sin(Time.time));
        Vector3 c = C1.position;
        Vector3 dir = (C2.position - C1.position).normalized;
        Vector3 v = Vertex.position;
        Vector3 vv = getVerticalVertex(c, dir, v);
#if UNITY_EDITOR
        Debug.DrawLine(c, C2.position, Color.black);
        Debug.DrawLine(v, vv, Color.red);
#endif
    }

    private Vector3 getVerticalVertex(Vector3 c, Vector3 dir, Vector3 v)
    {
        //首先写出推导过程（不参与计算）
        float n = 0;
        Vector3 p = c + n * dir;
        Vector3 pc = n * dir;
        Vector3 pv = v - p;
        pv = v - c - n * dir;
        //接着根据公式计算一元二次方程的根
        //pc.x * pv.x + pc.y * pv.y + pc.z * pv.z = 0;
        //n^2*(dir.x^2+dir.y^2+dir.z^2)+n*(dir.x*c.x-dir.x*v.x+dir.y*c.y-dir.y*v.y+dir.z*c.z-dir.z*v.z)=0
        //构建一元二次方程组参数
        float A = dir.x * dir.x + dir.y * dir.y + dir.z * dir.z;
        float B = dir.x * c.x - dir.x * v.x + dir.y * c.y - dir.y * v.y + dir.z * c.z - dir.z * v.z;
        float C = 0;
        //去掉n为0的根
        float n1 = (-B + Mathf.Sqrt(B * B - 4 * A * C)) / (2 * A);
        if (n1 != 0)
        {
            return c + n1 * dir;
        }
        float n2 = (-B - Mathf.Sqrt(B * B - 4 * A * C)) / (2 * A);
        if (n2 != 0)
        {
            return c + n2 * dir;
        }
        return c;
    }
}

     这里我们将n=0的情况的方程根去掉，因为n=0的情况下，C1和P重合，就失去了计算点积和垂直的意义。最后效果图如下：

  

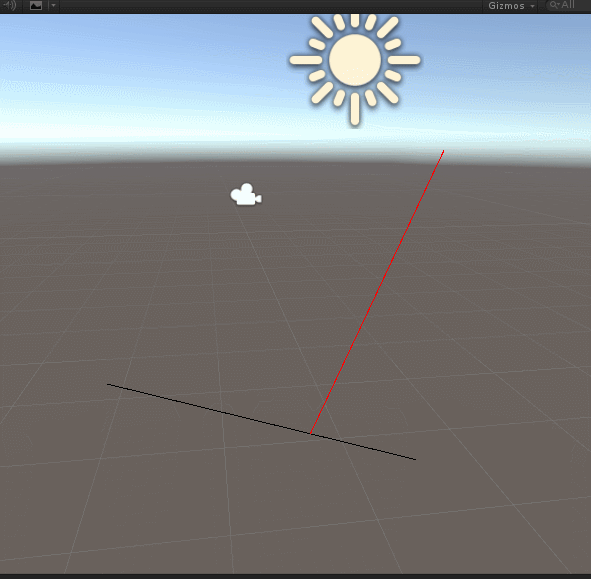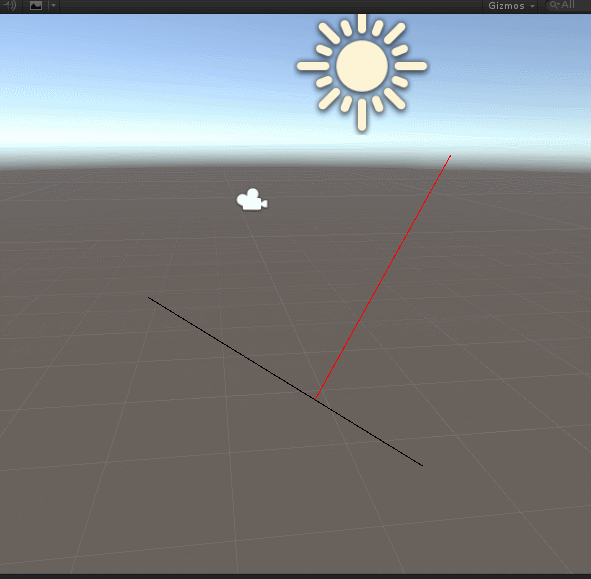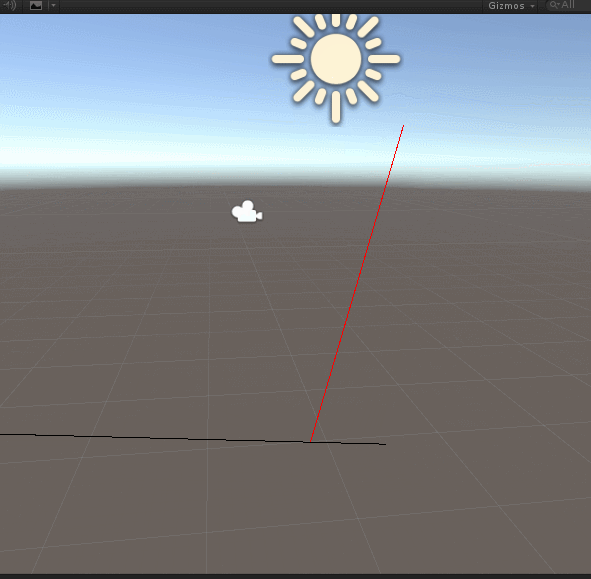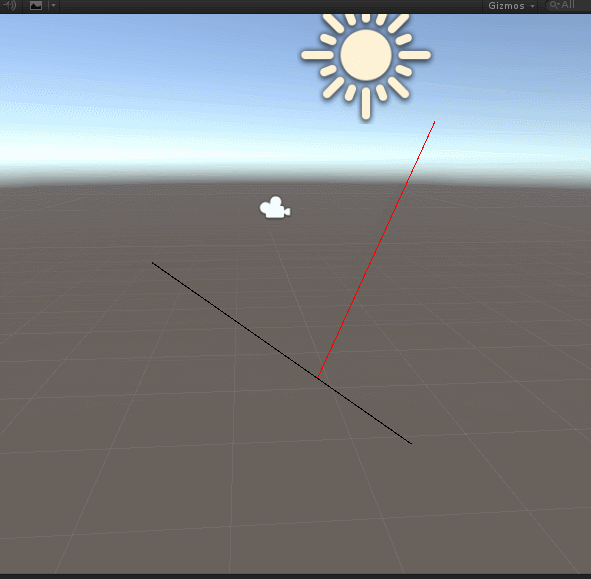
    看得出来，计算的垂点正确。