FVC与地表温度的相关性分析研究

植被覆盖度计算
植被覆盖度通常是指绿色植被群体经阳光照射后在地面上形成的垂直投影面积与整个研究区域面积之比，获取植被覆盖度信息主要有植被指数法和混合像元法。本文采用混合像元法进行计算，混合像元法是基于地物光谱的混合模型，在缺乏地面实测资料的情况下，该技术可以直接确定植被覆盖度。
NDVI的计算公式: NDVI= (NIR-R) / (NIR+R)
对于landsat8影像数据，NIR (近红波段)为波段5，R (红波段)
为波段4

NDVI与植被覆盖度转换公式:
FVC =(NDVI - NDV Imin)/(NDV Imax- NDV Imin)

地表温度计算
获取城市地表温度主要有以下三种方法:单通道算法、分裂窗算法和大气校正法。研究经验表明，大气校正法由于适用于任何热红外波段而被广泛使用。因此本文采取大气校正法，即辐射传导方程( Radiation Transfer Equation，RTE )，将获得的地表温.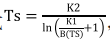
度转化为摄氏度。

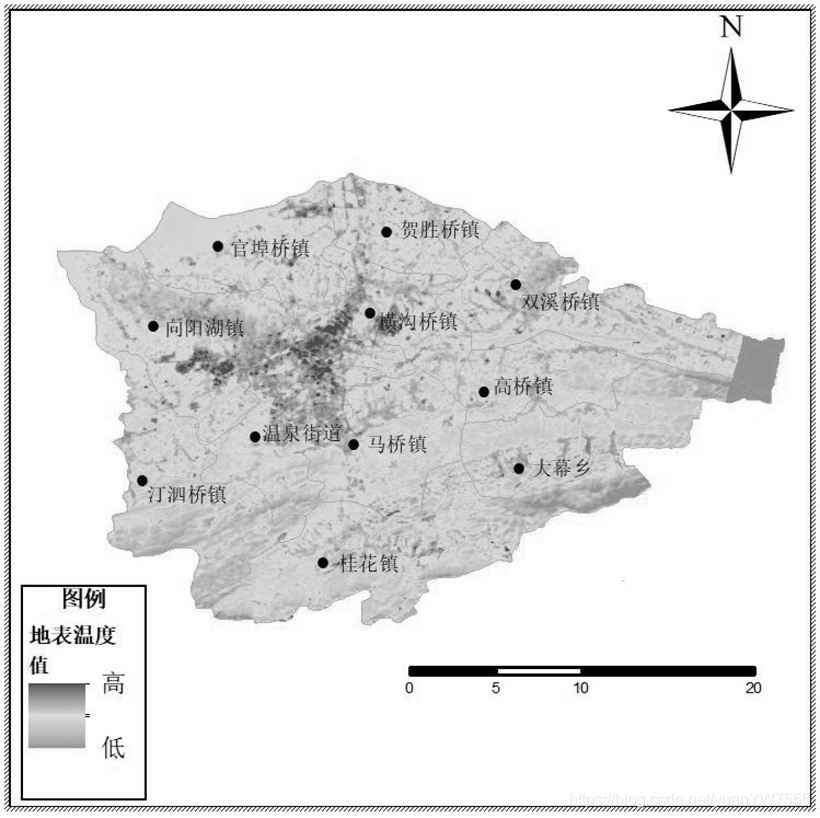
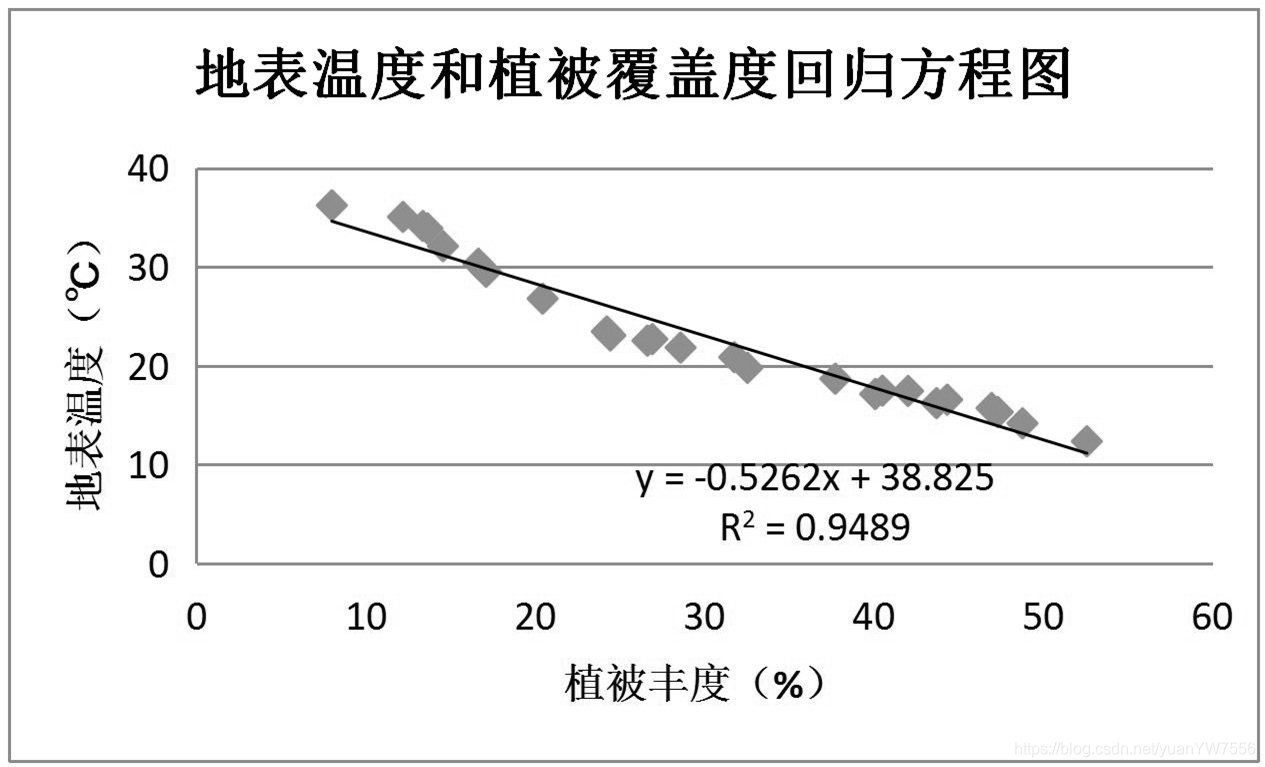
为了验证植被覆盖度和地表温度分布情况得出的初步结论，需要在研究区范围内选取了样本点，进行植被覆盖度和地表温度的相关性分析，由于城区内的绿色植被、水体会受周围环境因素的影响，这些区域的地表温度会偏高。为消除误差值对结果的影响，本文在研究区范围选择性选取了部分样本点生成散点图，建立线性回归方程，并将相关性和协方差在回归方程图中显示。最后求得咸安区植被覆盖度和地表温度的相关系数为-0.5262，在0.01的置信水平上负相关。可以看出，咸安区植被覆盖度和地表温度存在明显的负相关性，即植被覆盖度越高，地表温度就越低。