非周期连续函数的傅里叶变换

 首先 我们把一个非周期信号扩展成一个周期信号 然后用傅里叶级数展开 也可以得到对应的级数系数

利用周期趋向于无穷大 可以把傅里叶级数展开就变成了一个积分

而神奇的是积分里其实还有一个积分

这样我们就得到了傅里叶变换对

我们把里面的积分成为函数的傅里叶变换

把外面的积分成为傅里叶逆变换

 

这一段非常重要 对于周期信号 我们用离散的复指数信号表示 他的模是ak 而对于非周期信号 这些复指数出现在连续的频率上 幅度也比较奇怪 就不写了 而傅里叶级数的频谱是ak 那么傅里叶变换到频谱就是积分里的xjw 也就是里面的那个积分

后面还有个例子 如果一个非周期信号是周期信号的一部分 那么 对于周期信号的傅里叶级数系数ak 是正比于傅里叶变换的样本  

这里提到了傅里叶变换到对偶性 原函数是矩形脉冲 傅里叶变换就是sinc函数 而原函数是sinc函数 那么傅里叶变换就是矩形脉冲

 

这里推导出来周期信号的傅里叶变换 就是对应傅里叶级数的谐波频率处的脉冲信号 大小和傅里叶级数也有关系

复习下

周期信号不论是离散还是连续 他的傅里叶级数都是离散的 而非周期信号的傅里叶变换是连续的 对应的周期信号的傅里叶变换 则是离散的 

不过离散的非周期信号我们还没碰到

这里把傅里叶级数的傅里叶变换也搞了出来 方便统一

可以看到 现在所有的都有了傅里叶变换 我们可以在频域一起对这些 信号进行分析

但这里最重要的思路我们要记得

对于非周期信号 我们先把他扩充成周期信号 然后做傅里叶级数展开 然后根据公式算ak 再把ak带入 得到x的表达式 再利用t趋向无穷 可以看成一个积分

但里面的积分是傅里叶变换 也就是求系数ak的积分

ak表示在对应频率上振幅的大小 这和傅里叶变换是一致的 周期信号的傅里叶变换公式 先求的ak 然后和冲击信号乘积 还有个倍数因子

 

这里提到了极坐标表示和奇函数偶函数 值得一看

不过我有个疑惑 傅里叶变换对周期函数也成立么

 

这里怼磁带播放速度有个很有意思的说明 如果播放速度变快 那么周期就变短了 频率就变高了  

这里讲了理想低通滤波器的一个问题 就是在时域上不是因果 同时 还有震荡的特性

 

而非理想滤波器 是因果的 而且是单调递减的

不过这里有个疑惑 为什么频率要有负的 其实之前我们看过 对于实信号 我们需要把复指数信号输入中的虚数的系数为0 所以他必须是轴对称的

让我们再回忆下傅里叶变换 首先是傅里叶级数 是对周期信号进行的基分解 然后我们考虑周期趋向于无穷 这个时候 傅里叶级数的系数是一个积分 但因为周期趋向于无穷 所以外面又可以看成一个积分 但我们还是关注里面的积分 所以傅里叶变换关注的还是原函数的基分解 不过现在的基是连续的基

所以 按照线性时不变系统的性质 我们将一个函数分解成一组基的表示 那么自然的 我们只要知道系统对基的响应 自然也就知道它对函数的响应 然后问题来了 要怎么知道系统函数对基的响应 这组基是复指数信号 我们一般只知道脉冲信号的响应 儿通过脉冲信号 可以知道复指数信号 如下

 

所以 我们通过脉冲信号响应得到复指数信号响应 剩下就是进行卷积即可

又因为良好的对称性 其实相当于频域上的乘积 然后逆变换回时域上

所以

我们用傅里叶变换得到了基的系数 同时基的响应又是线性放大 这个放大的系数是脉冲响应的傅里叶变换

所以我们要把信号本身的傅里叶变换和脉冲响应的傅里叶变换乘起来 再乘以基 

所以一个原始信号和系统脉冲响应的卷积 就是他们的傅里叶变换的乘积

z

这样才好理解这个例子

 

 

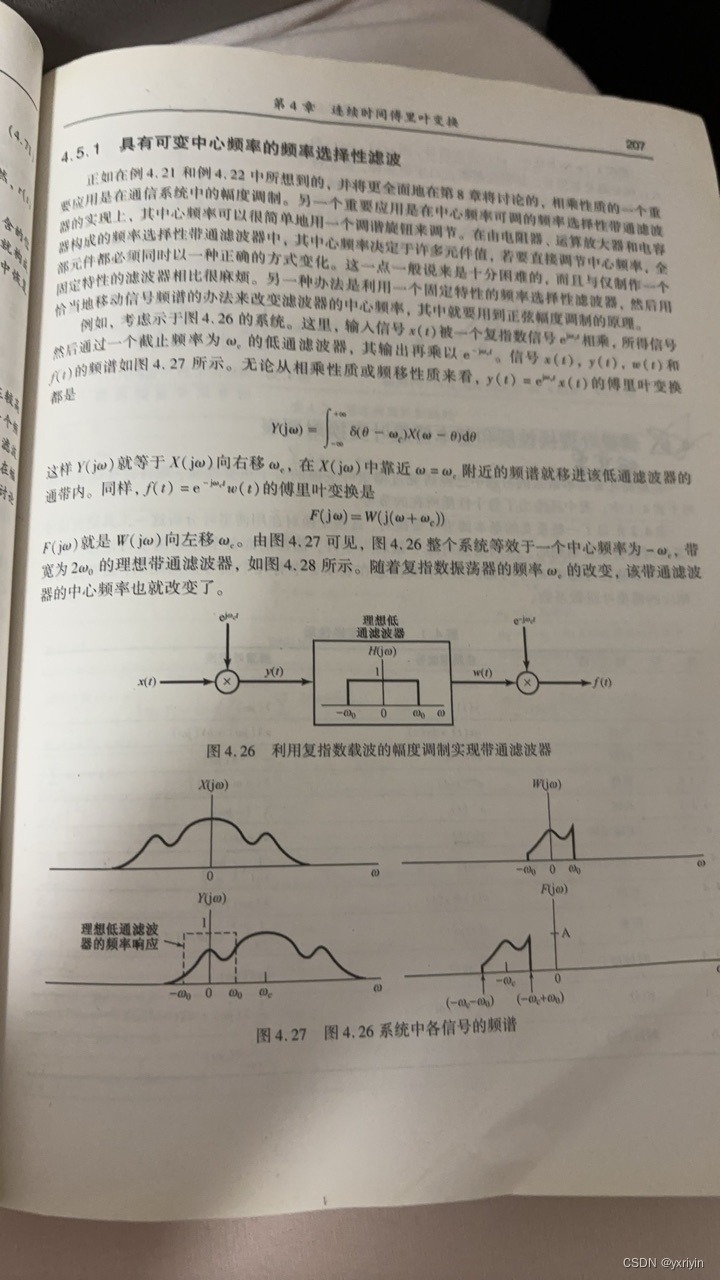
这个应该印刷不对 少了个j

所以最后复述下全部的概念

首先我们有了周期函数的傅里叶级数

推广到非周期函数 就得到了系数的公式 叫做傅里叶变换

然后周期函数的傅里叶级数的系数是离散的 但非周期函数的傅里叶变换的系数是连续的

同时 比起之前用脉冲信号分解函数 我们现在更希望用复指数函数作为基 它是线性时不变系统的特征函数

所以按照之前卷积的概念 我们先把输入信号分解成基的线性组合 然后根据每个基的响应求和 就会得到最终的响应 基的响应是一个脉冲响应的积分 称为系统的频率响应 而基的系数就是x的傅里叶变换 于是就可以得到全新的卷积性质 时域的卷积等于频域的乘积